Statistics review 6: Nonparametric methods

Abstract

The present review introduces nonparametric methods. Three of the more common nonparametric methods are described in detail, and the advantages and disadvantages of nonparametric versus parametric methods in general are discussed.

Introduction

Many statistical methods require assumptions to be made about the format of the data to be analysed. For example, the paired t-test introduced in Statistics review 5 requires that the distribution of the differences be approximately Normal, while the unpaired t-test requires an assumption of Normality to hold separately for both sets of observations. Fortunately, these assumptions are often valid in clinical data, and where they are not true of the raw data it is often possible to apply a suitable transformation. There are situations in which even transformed data may not satisfy the assumptions, however, and in these cases it may be inappropriate to use traditional (parametric) methods of analysis. (Methods such as the t-test are known as 'parametric' because they require estimation of the parameters that define the underlying distribution of the data; in the case of the t-test, for instance, these parameters are the mean and standard deviation that define the Normal distribution.)

Nonparametric methods provide an alternative series of statistical methods that require no or very limited assumptions to be made about the data. There is a wide range of methods that can be used in different circumstances, but some of the more commonly used are the nonparametric alternatives to the t-tests, and it is these that are covered in the present review.

The sign test

The sign test is probably the simplest of all the nonparametric methods. It is used to compare a single sample with some hypothesized value, and it is therefore of use in those situations in which the one-sample or paired t-test might traditionally be applied. For example, Table 1 presents the relative risk of mortality from 16 studies in which the outcome of septic patients who developed acute renal failure as a complication was compared with outcomes in those who did not. The relative risk calculated in each study compares the risk of dying between patients with renal failure and those without. A relative risk of 1.0 is consistent with no effect, whereas relative risks less than and greater than 1.0 are suggestive of a beneficial or detrimental effect of developing acute renal failure in sepsis, respectively. Does the combined evidence from all 16 studies suggest that developing acute renal failure as a complication of sepsis impacts on mortality?

Table 1.

Relative risk of mortality associated with developing acute renal failure as a complication of sepsis

Study	Relative risk	Sign
1	0.75	-
2	2.03	+
3	2.29	+
4	2.11	+
5	0.80	-
6	1.50	+
7	0.79	-
8	1.01	+
9	1.23	+
10	1.48	+
11	2.45	+
12	1.02	+
13	1.03	+
14	1.30	+
15	1.54	+
16	1.27	+

Fig. 1 shows a plot of the 16 relative risks. The distribution of the relative risks is not Normal, and so the main assumption required for the one-sample t-test is not valid in this case. Rather than apply a transformation to these data, it is convenient to use a nonparametric method known as the sign test.

Figure 1.

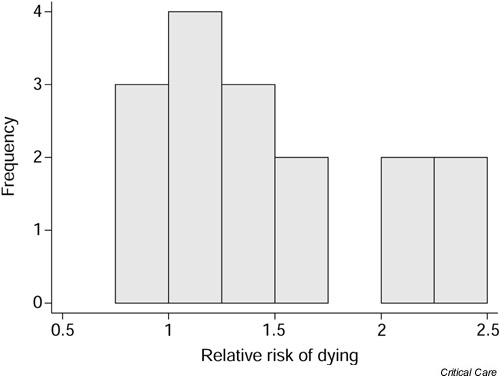
Relative risk of mortality associated with developing acute renal failure as a complication of sepsis.

The sign test is so called because it allocates a sign, either positive (+) or negative (-), to each observation according to whether it is greater or less than some hypothesized value, and considers whether this is substantially different from what we would expect by chance. If any observations are exactly equal to the hypothesized value they are ignored and dropped from the sample size. For example, if there were no effect of developing acute renal failure on the outcome from sepsis, around half of the 16 studies shown in Table 1 would be expected to have a relative risk less than 1.0 (a 'negative' sign) and the remainder would be expected to have a relative risk greater than 1.0 (a 'positive' sign). In this case only three studies had a relative risk of less than 1.0 whereas 13 had a relative risk above this value. It is not unexpected that the number of relative risks less than 1.0 is not exactly 8; the more pertinent question is how unexpected is the value of 3? The sign test gives a formal assessment of this.

Formally the sign test consists of the steps shown in Table 2. In this example the null hypothesis is that there is no increase in mortality when septic patients develop acute renal failure.

Table 2.

Steps required in performing the sign test

Step	Details
1	State the null hypothesis and, in particular, the hypothesized value for comparison
2	Allocate a sign (+ or -) to each observation according to whether it is greater or less than the hypothesized value. (Observations exactly equal to the hypothesized value are dropped from the analysis)
3	Determine:
	N+ = the number of observations greater than the hypothesized value
	N- = the number of observations less than the hypothesized value
	S = the smaller of N+ and N-
4	Calculate an appropriate P value

Exact P values for the sign test are based on the Binomial distribution (see Kirkwood [1] for a description of how and when the Binomial distribution is used), and many statistical packages provide these directly. However, it is also possible to use tables of critical values (for example [2]) to obtain approximate P values.

The counts of positive and negative signs in the acute renal failure in sepsis example were N₊ = 13 and N_- = 3, and S (the test statistic) is equal to the smaller of these (i.e. N_-). The critical values for a sample size of 16 are shown in Table 3. S is less than or equal to the critical values for P = 0.10 and P = 0.05. However, S is strictly greater than the critical value for P = 0.01, so the best estimate of P from tabulated values is 0.05. In fact, an exact P value based on the Binomial distribution is 0.02. (Note that the P value from tabulated values is more conservative [i.e. larger] than the exact value.) In other words there is some limited evidence to support the notion that developing acute renal failure in sepsis increases mortality beyond that expected by chance.

Table 3.

Critical values for the sign test with a sample size of 16

P value	0.10	0.05	0.01
Critical value	4	3	2

Note that the sign test merely explores the role of chance in explaining the relationship; it gives no direct estimate of the size of any effect. Although it is often possible to obtain non-parametric estimates of effect and associated confidence intervals in principal, the methods involved tend to be complex in practice and are not widely available in standard statistical software. This lack of a straightforward effect estimate is an important drawback of nonparametric methods.

The sign test can also be used to explore paired data. Consider the example introduced in Statistics review 5 of central venous oxygen saturation (SvO₂) data from 10 consecutive patients on admission and 6 hours after admission to the intensive care unit (ICU). The paired differences are shown in Table 4. In this example, the null hypothesis is that there is no effect of 6 hours of ICU treatment on SvO₂. In other words, under the null hypothesis, the mean of the differences between SvO₂ at admission and that at 6 hours after admission would be zero. In terms of the sign test, this means that approximately half of the differences would be expected to be below zero (negative), whereas the other half would be above zero (positive).

Table 4.

Central venous oxygen saturation on admission and 6 hours after admission

	SvO2 (%)
Patient	On admission	6 hours	Difference	Sign
1	39.7	52.9	13.2	+
2	59.1	56.7	-2.4	-
3	56.1	61.9	5.8	+
4	57.7	71.4	13.7	+
5	60.6	67.7	7.1	+
6	37.8	50.0	12.2	+
7	58.2	60.7	2.5	+
8	33.6	51.3	17.7	+
9	56.0	59.5	3.5	+
10	65.3	59.8	-5.5	-

SvO₂ = central venous oxygen saturation.

In practice only 2 differences were less than zero, but the probability of this occurring by chance if the null hypothesis is true is 0.11 (using the Binomial distribution). In other words, it is reasonably likely that this apparent discrepancy has arisen just by chance. Note that the paired t-test carried out in Statistics review 5 resulted in a corresponding P value of 0.02, which appears at a first glance to contradict the results of the sign test. It is not necessarily surprising that two tests on the same data produce different results. The apparent discrepancy may be a result of the different assumptions required; in particular, the paired t-test requires that the differences be Normally distributed, whereas the sign test only requires that they are independent of one another. Alternatively, the discrepancy may be a result of the difference in power provided by the two tests. As a rule, nonparametric methods, particularly when used in small samples, have rather less power (i.e. less chance of detecting a true effect where one exists) than their parametric equivalents, and this is particularly true of the sign test (see Siegel and Castellan [3] for further details).

The Wilcoxon signed rank test

The sign test is intuitive and extremely simple to perform. However, one immediately obvious disadvantage is that it simply allocates a sign to each observation, according to whether it lies above or below some hypothesized value, and does not take the magnitude of the observation into account. Omitting information on the magnitude of the observations is rather inefficient and may reduce the statistical power of the test. An alternative that does account for the magnitude of the observations is the Wilcoxon signed rank test. The Wilcoxon signed rank test consists of five basic steps (Table 5).

Table 5.

Steps required in performing the Wilcoxon signed rank test

Step	Details
1	State the null hypothesis and, in particular, the hypothesized value for comparison
2	Rank all observations in increasing order of magnitude, ignoring their sign. Ignore any observations that are equal to the hypothesized value. If two observations have the same magnitude, regardless of sign, then they are given an average ranking
3	Allocate a sign (+ or -) to each observation according to whether it is greater or less than the hypothesized value (as in the sign test)
4	Calculate:
	R+ = sum of all positive ranks
	R- = sum of all negative ranks
	R = smaller of R+ and R-
5	Calculate an appropriate P value

To illustrate, consider the SvO₂ example described above. The sign test simply calculated the number of differences above and below zero and compared this with the expected number. In the Wilcoxon rank sum test, the sizes of the differences are also accounted for.

Table 6 shows the SvO2 at admission and 6 hours after admission for the 10 patients, along with the associated ranking and signs of the observations (allocated according to whether the difference is above or below the hypothesized value of zero). Note that if patient 3 had a difference in admission and 6 hour SvO₂ of 5.5% rather than 5.8%, then that patient and patient 10 would have been given an equal, average rank of 4.5.

Table 6.

Central venous oxygen saturation on admission and 6 hours after admission

	SvO2 (%)
Patient	On admission	At 6 hours	Difference	Rank	Sign
2	59.1	56.7	-2.4	1	-
7	58.2	60.7	2.5	2	+
9	56.0	59.5	3.5	3	+
10	65.3	59.8	-5.5	4	-
3	56.1	61.9	5.8	5	+
5	60.6	67.7	7.1	6	+
6	37.8	50.0	12.2	7	+
1	39.7	52.9	13.2	8	+
4	57.7	71.4	13.7	9	+
8	33.6	51.3	17.7	10	+

The sums of the positive (R₊) and the negative (R_-) ranks are as follows.

R₊ = 2 + 3 + 5 + 6 + 7 + 8 + 9 + 10 = 50

R_- = 1 + 4 = 5

Thus, the smaller of R₊ and R_- (R) is as follows.

R = R_- = 5

As with the sign test, a P value for a small sample size such as this can be obtained from tabulated values such as those shown in Table 7. The calculated value of R (i.e. 5) is less than or equal to the critical values for P = 0.10 and P = 0.05 but greater than that for P = 0.01, and so it can be concluded that P is between 0.01 and 0.05. In other words, there is some evidence to suggest that there is a difference between admission and 6 hour SvO₂ beyond that expected by chance. Notice that this is consistent with the results from the paired t-test described in Statistics review 5. P values for larger sample sizes (greater than 20 or 30, say) can be calculated based on a Normal distribution for the test statistic (see Altman [4] for details). Again, the Wilcoxon signed rank test gives a P value only and provides no straightforward estimate of the magnitude of any effect.

Table 7.

Critical values for the Wilcoxon signed rank test with a sample size of 10

P value	0.10	0.05	0.01
Critical value	10	8	3

The Wilcoxon rank sum or Mann–Whitney test

The sign test and Wilcoxon signed rank test are useful non-parametric alternatives to the one-sample and paired t-tests. A nonparametric alternative to the unpaired t-test is given by the Wilcoxon rank sum test, which is also known as the Mann–Whitney test. This is used when comparison is made between two independent groups. The approach is similar to that of the Wilcoxon signed rank test and consists of three steps (Table 8).

Table 8.

Steps required in performing the Wilcoxon rank sum (Mann–Whitney) test

Step	Details
1	Rank all observations in increasing order of magnitude, ignoring which group they come from. If two observations have the same magnitude, regardless of group, then they are given an average ranking
2	Add up the ranks in the smaller of the two groups (S). If the two groups are of equal size then either one can be chosen
3	Calculate an appropriate P value

The data in Table 9 are taken from a pilot study that set out to examine whether protocolizing sedative administration reduced the total dose of propofol given. Patients were divided into groups on the basis of their duration of stay. The data presented here are taken from the group of patients who stayed for 3–5 days in the ICU. The total dose of propofol administered to each patient is ranked by increasing magnitude, regardless of whether the patient was in the protocolized or nonprotocolized group. Note that two patients had total doses of 21.6 g, and these are allocated an equal, average ranking of 7.5. There were a total of 11 nonprotocol-ized and nine protocolized patients, and the sum of the ranks of the smaller, protocolized group (S) is 84.5.

Table 9.

Total propofol doses in patients with a 3 to 5 day stay in the intensive care unit

Nonprotocolized group		Protocolized group
Dose (g)	Rank	Dose (g)	Rank
7.2	2	5.6	1
15.7	4	14.6	3
19.1	6	18.2	5
21.6	7.5	21.6	7.5
26.8	10	23.1	9
27.4	11	28.3	12
28.5	13	31.7	14
32.8	16	32.4	15
36.3	17	36.8	18
43.2	19
44.7	20
			S = 84.5

Again, a P value for a small sample such as this can be obtained from tabulated values. In this case the two individual sample sizes are used to identify the appropriate critical values, and these are expressed in terms of a range as shown in Table 10. The range in each case represents the sum of the ranks outside which the calculated statistic S must fall to reach that level of significance. In other words, for a P value below 0.05, S must either be less than or equal to 68 or greater than or equal to 121. In this case S = 84.5, and so P is greater than 0.05. In other words, this test provides no evidence to support the notion that the group who received protocolized sedation received lower total doses of propofol beyond that expected through chance. Again, for larger sample sizes (greater than 20 or 30) P values can be calculated using a Normal distribution for S [4].

Table 10.

Critical values for the Wilcoxon rank sum test with sample sizes of 9 and 11

P value	0.05	0.01	0.001
Critical value	68–121	61–128	53–136

Advantages and disadvantages of nonparametric methods

Inevitably there are advantages and disadvantages to non-parametric versus parametric methods, and the decision regarding which method is most appropriate depends very much on individual circumstances. As a general guide, the following (not exhaustive) guidelines are provided.

Advantages of nonparametric methods

Nonparametric methods require no or very limited assumptions to be made about the format of the data, and they may therefore be preferable when the assumptions required for parametric methods are not valid.

Nonparametric methods can be useful for dealing with unexpected, outlying observations that might be problematic with a parametric approach.

Nonparametric methods are intuitive and are simple to carry out by hand, for small samples at least.

Nonparametric methods are often useful in the analysis of ordered categorical data in which assignation of scores to individual categories may be inappropriate. For example, non-parametric methods can be used to analyse alcohol consumption directly using the categories never, a few times per year, monthly, weekly, a few times per week, daily and a few times per day. In contrast, parametric methods require scores (i.e. 1–7) to be assigned to each category, with the implicit assumption that the effect of moving from one category to the next is fixed.

Disadvantages of nonparametric methods

Nonparametric methods may lack power as compared with more traditional approaches [3]. This is a particular concern if the sample size is small or if the assumptions for the corresponding parametric method (e.g. Normality of the data) hold.

Nonparametric methods are geared toward hypothesis testing rather than estimation of effects. It is often possible to obtain nonparametric estimates and associated confidence intervals, but this is not generally straightforward.

Tied values can be problematic when these are common, and adjustments to the test statistic may be necessary.

Appropriate computer software for nonparametric methods can be limited, although the situation is improving. In addition, how a software package deals with tied values or how it obtains appropriate P values may not always be obvious.

Competing interests

None declared.

Note

This article is the sixth in an ongoing, educational review series on medical statistics in critical care. Previous articles have covered 'presenting and summarizing data', 'samples and populations', 'hypotheses testing and P values', 'sample size calculations' and 'comparison of means'. Future topics to be covered include simple regression, comparison of proportions and analysis of survival data, to name but a few. If there is a medical statistics topic you would like explained, contact us on editorial@ccforum.com.

Abbreviations

ICU = intensive care unit; SvO₂ = central venous oxygen saturation.