The use of a physiologically based pharmacokinetic model to evaluate deconvolution measurements of systemic absorption

Abstract

Background

An unknown input function can be determined by deconvolution using the systemic bolus input function (r) determined using an experimental input of duration ranging from a few seconds to many minutes. The quantitative relation between the duration of the input and the accuracy of r is unknown. Although a large number of deconvolution procedures have been described, these routines are not available in a convenient software package.

Methods

Four deconvolution methods are implemented in a new, user-friendly software program (PKQuest, http://www.pkquest.com). Three of these methods are characterized by input parameters that are adjusted by the user to provide the "best" fit. A new approach is used to determine these parameters, based on the assumption that the input can be approximated by a gamma distribution. Deconvolution methodologies are evaluated using data generated from a physiologically based pharmacokinetic model (PBPK).

Results and Conclusions

The 11-compartment PBPK model is accurately described by either a 2 or 3-exponential function, depending on whether or not there is significant tissue binding. For an accurate estimate of r the first venous sample should be at or before the end of the constant infusion and a long (10 minute) constant infusion is preferable to a bolus injection. For noisy data, a gamma distribution deconvolution provides the best result if the input has the form of a gamma distribution. For other input functions, good results are obtained using deconvolution methods based on modeling the input with either a B-spline or uniform dense set of time points.

Background

The deconvolution approach has become a commonly used technique to determine the time course of a systemic input (I(t)) to a linear system given the system response to a known bolus intravenous (IV) input . This approach is based on the following fundamental equation:

where r(t) is the systemic (e.g. venous) concentration that is produced by a bolus systemic input of unit amount ("bolus response function"); I(t) is the unknown systemic input rate (for example, from an oral dose); and c(t) is the systemic (e.g. venous) concentration that is produced by the unknown systemic input I(t). For example, if r(t) is the venous concentration from a bolus IV injection of 1 g of X, and c(t) is the venous concentration after the oral ingestion of X, then I(t) corresponds to the rate (in g/min) that this oral dose of X reaches the systemic circulation. If there is no liver metabolism of X, then I(t) is equal to the rate of intestinal absorption of X. If there is some liver metabolism (i.e. first pass metabolism), then I(t) is a measure of the systemic availability of X after an oral dose.

There are two separate problems that must be addressed in order to find I(t). The first is the determination of bolus input function r(t). This involves finding a continuous function that provides a good approximation to r(t) given the discrete set of venous concentrations determined, e.g., after a constant IV infusion. The second problem is, given r(t), estimate I(t) using the discrete set of data points for c(t).

While there is a voluminous literature that addresses the second problem [1-13], little attention has been paid to the first problem. The first part of this paper uses a physiologically based pharmacokinetic model (PBPK) to address the following two questions about this standard approach:

1) It is usually assumed that r(t) can be approximated by a 2 or 3 exponential function. The standard approach is to fit experimental data with both a 2 and 3 exponential function and use statistical tests to determine whether the additional adjustable parameters have significantly improved the fit, given the experimental error. From these measurements one cannot separate errors in experimental measurement from intrinsic limitations in the multi-exponential functional description of the system. It would be desirable to test the ability of multi-exponential functions to describe r(t) for error free data. In this paper, multi-exponential functions will be used to fit exact data generated using a PBPK model that mimics the detailed human pharmacokinetics. One would expect that a 2 or 3-exponential function would only provide a crude approximation to the complicated 11 compartment PBPK model.

2) The bolus input function r(t) is determined by fitting venous data produced by a known constant IV infusion. The duration of this infusion can vary from a few seconds (mimicking a "bolus" input) to 20 or more minutes. Obviously, one would like to sample the venous concentration over the entire time course. However, because of unavoidable circulatory and mixing time delays, venous concentration measurements for time points earlier than 2 or 3 minutes are not reliable. The earliest experimental venous concentration measurements that are used to determine the bolus input function r(t) are often at 5 or 10 minutes and, in some cases, as long as 60 minutes [12]. Although it seems intuitively clear that, in order to avoid the need for early time sampling, one should use an IV infusion of relatively long duration, this question has not been looked at quantitatively. In this paper, PBPK human models will be used to quantitatively investigate the relationship between the duration of the constant IV infusion and the venous sampling rate required for an accurate estimate of r(t).

The second part of this paper addresses the second problem in the determination of I(t) – how to solve for I(t) once r(t) is known. Since this poses a challenging mathematical problem, it has elicited a number of sophisticated numerical solutions from a large number of investigators. The following four fundamentally different approaches are examined in this paper:

Gamma distribution Input

The use of a predetermined parametric function for I(t) is the most direct approach. It is shown below that a good fit to a variety of experimental intestinal absorption processes is provided by the 3 parameter (A,a,b) gamma distribution:

(2)     I(t) = Ab^at^a-1 exp(-bt)/Γ(a)

where A is the total amount reaching the systemic circulation, Γ is the gamma function, a is the gamma number (usually between 1.0 and 6.0) and b has units of inverse time. The gamma distribution is clearly superior to poly-exponential functions for fitting the initial time delay in absorption associated with gastric emptying. The use of a gamma distribution to model absorption was first suggested by Debord et. al. [2]. The 3 parameters are determined by the use of global (simulated annealing) and local (Powell) non-linear optimization.

Analytical Deconvolution

In this approach, c(t) (eq. 1) is approximated by an interpolating or smoothed spline function and the deconvolution uses the analytic approach of Veng-Pedersen [14,15] and Gilespie and Veng-Pedersen [3]. This approach is used in the freely distributed program PCDCON written by Gillespie http://anesthesia.stanford.edu/pkpd and is the most widely used experimental deconvolution technique [16-21].

Spline Function Input

This method uses the approach of Verotta [4,5] in which the input I(t) is parameterized by a general B-spline function and the deconvolution is obtained using constrained regression.

Uniform Input

In this approach the function I(t) is estimated on a dense, uniform sequence of time points and the stochastic regularization procedure of De Nicolao et. al. [1] and Sparacino et. al. [22,23] is used for the deconvolution.

Since each of these approaches has been extensively described and compared previously, what justifies the new treatment in this paper? There are 3 new features:

1) The four above mathematical approaches to the deconvolution problem are implemented in the software package PKQuest. This software has a simple user interface, and automatically plots the results in a variety of formats. This easy to use, freely distributed program http://www.pkquest.com allows anyone to use and compare the different approaches for different experimental data sets.

2) The last 3 approaches are characterized by a number of user input parameters whose values are not known a priori. In the previous applications of these routines, these parameters had to be varied and the "best" value found either based on the subjective judgment of the user about the "quality" of the fit, or by a semi-empirical optimization procedure. This represents the major limitation of these techniques. In this paper a new method is introduced for determining the value of these parameters for the last two methods ("Spline function" and "Uniform") based on the use of a gamma distribution approximation for I(t).

3) Previous tests of the different approaches have used either idealized model data or experimental data in which the true values of the bolus input function r(t) and the systemic input function I(t) were not known. In contrast, in the analysis described here, the different methods will be tested using the same PBPK model that was used to determine r(t). In general, all the methods work well if accurate experimental data are used (see below). The most stringent test of the different methods is under conditions when there is random error in the data points and sampling frequency is limited, as is often the case for the experimental data. This latter case is investigated in this paper.

Methods

Generation of PBPK Model Venous Concentration Data

The model venous concentration data for the intravenous (IV) and intestinal input are generated using the PKQuest http://www.pkquest.com PBPK software. The "standard human" PBPK organ weights and blood flows are listed in Table I. These are the same values that have been used previously to model the pharmacokinetics of D₂O and ethanol [24], toluene and the volatile anesthetics [25], propranolol [26] and inulin and protein bound antibiotics [27]. Two different PBPK models are used. In the first model (referred to as "simple") the solute distributes with flow-limited kinetics in all the body water and there is no solute binding. In the second model (referred to as "binding") the different tissues bind the solute with a tissue/plasma equilibrium partition coefficient of 10 for all tissues except muscle (where it is 3.62) and fat (where it is 2.42). This model is similar to that used to describe human propranolol pharmacokinetics [26]. The model input goes directly into the venous compartment, bypassing the liver, and the solute clearance is produced entirely by renal secretion so that the input function ("absorption" rate) is equal to the systemic availability.

Table 1.

Organ Weights and Blood Flows for Standard Human (70 Kg, 20% Fat)

Organ	Weight (Kg)	Blood Flow (lit/min/Kg)
Artery	1.1	----
Vein	4.4	----
Liver	1.8	0.25 (hepatic artery)
Portal	1.5	0.75 (portal vein)
Kidney	0.31	4.0
muscle	33.0	0.0266
brain	1.4	0.56
heart	0.33	0.8
lung	0.536	14.98
skin	2.6	0.12
fat	14	0.056
"other"	4.12	0.054
"bone"	4.90.	0.0

Determination of Poly-exponential Bolus Response Function

The standard approach is used for determining the bolus response function r(t). It is assumed that r(t) is described by a polyexponentials function:

The optimum values for the parameters (a_i, T_i) are determined by using the Maple implementation of the non-linear Levenberg and Marquardt method (nlfit, http://www.math.villanova.edu/archives/maple/misc). Some care must be used in the application of this technique because, if the initial estimates of a_i and T_i are far from the correct values then, for the 3-exponential case, it is possible for the solution to become stuck in a local minimum, far from the global minimum. In the implementation in PKQuest, a 2- exponential fit is found first, and this fit is used to estimate the initial values for the 3-exponential fit. This procedure seems to be quite robust.

Gamma distribution Deconvolution

It is assumed that the input function can be described by a 3 parameter (A,a,b) gamma distribution (eq. 2). The 3 parameters are chosen by minimizing the error function:

where the sum is over all the data points, ydat_i is the experimental venous concentration, and ygam_i is the venous concentration determined by convoluting the gamma distribution input (eq. 2) with the polyexponential bolus response function r(t) (eq. 3). The parameter "noise" determines the relative weighting of each data point. If noise = 0, then the error is proportional to the sum of the fractional error ((ygam-ydat)/ydat) of each point, while for noise>>ydat, the error is proportional to the sum of the absolute error (ygam-ydat) of each point. In the current implementation, noise is assumed to be equal to 10% of the value of average venous concentration (ydat_i). Since the convolution of the gamma distribution with r(t) is a highly non-linear function, it is essential to use a robust optimization procedure to avoid local minimums. In the implementation in PKQuest, a global annealing procedure [28] is applied first, followed by Powell [29] non-linear minimization.

Analytical Deconvolution

The approach described originally by Veng-Pederesen [14,15] is followed. The discrete venous concentration data (c [i], eq. 1) is fit with either an interpolating (which goes through each data point) or a smoothing cubic spline function, and then the deconvolution is obtained analytically using this spline function. The spline fitting algorithms of Spath [30] were used for both the interpolating ("cub2r7") and smoothing ("cubsm1") conditions. In the smoothing algorithm the spline points differ from the experimental data points by an amount that is proportional to the jump in the third derivative of the cubic spline function. The proportionality constant is assumed to be the same for each data point and is set by a user input "smoothing parameter" that varies from 0 (interpolating case) to infinity. This implementation is not identical to that used in program the PCDCON written by W. R. Gillespie http://anesthesia.stanford.edu/pkpd. However, when the same input was used for PCDCON and the current implementation, the results were very similar.

Spline Function Deconvolution

The deconvolution approach of Verotta [5] is used. The input function I(t) is parameterized by a B-spline function characterized by the number and position of the "breakpoints" and the order of the spline function. An order of 3 is assumed. The deconvolution is obtained using the "Penalized Least_Squares" regularization approach [5], where the regularization parameter (referred to here as a "smoothing parameter") limits the roughness of the B-spline function. The input rate I(t) is constrained to non-negative values by using the constrained conjugate gradient algorithm (11.4) of Hestenes [31].

The quality of the deconvolution solution is critically dependent on the number and position of the break points (see Results Section). In the implementation in PKQuest, a number of alternative options are allowed for choosing or inputting the break points. Since this method is a generalized parametric approach, one would like to use the smallest number of breakpoints (and, therefore, the fewest adjustable parameters) that are compatible with the input function. A new feature that is introduced here is the use of the gamma distribution input approximation to automatically select the breakpoints (this is the default option in PKQuest). This method first chooses the breakpoints that provide a good fit to the gamma distribution, and then supplements these breakpoints with additional points (at 1 hour intervals) at long times when the gamma distribution is small. By trial and error it was found that the minimum number of break points that provided a good fit to the gamma distribution were located at the times the gamma distribution concentration equaled 0.05, 0.7, 1, 0.55, 0.1 and 0.0012 times the maximum gamma distribution value. As shown in the Results Section, this procedure works well for the typical intestinal absorption input functions.

Uniform Input Deconvolution

The method of De Nicolao et. al. [1] which solves for the values of the input function on a uniform, dense set of time points is used. Only the constrained option [1] is used since it is essential to limit the input function to non-negative values. De Nicolao et. al. [1] describe a sophisticated mathematical approach using the fast fourier transform (FFT). However, in the implementation in PKQuest (using Maple) it was observed that the overhead required to set up the FFT approach used more CPU time than the more direct implementation that was finally adopted.

This approach is critically dependent on the "regularization" parameter (referred to in this paper as "smoothing parameter") and De Nicolao et. al. [1] described a number of criteria for choosing the "best" value of this parameter. In PKQuest, a new option is introduced that uses the gamma distribution input function to obtain a default value of the smoothing parameter. The error function that is minimized to determine the input vector U is the sum of two terms [1]:

(5)     Error Function = (Y - GU)^T (Y - GU) + γU^T (F^T F)U

In the first term the matrix (Y-GU) is a measure of the error difference between the experimental venous concentrations (Y) and the model values given by the convolution of the input vector (U) and bolus input function operator (G). The second term is a measure of the roughness of the data where γ is the smoothing parameter and F is the second difference matrix. The new procedure that is used to estimate the smoothing parameter (γ) is to set the input vector U equal to the approximate gamma input function and solve for the value of γ that makes the two terms in eq. 5 have equal weight. This calculation of γ is limited to time points where the value of the gamma distribution is greater than 1% of the peak value of the gamma distribution – that is, points where the gamma distribution provides a good approximation. Although this choice of equal weights is empirical and was based on trial and error on one set of data, it seems to work well for a large range of experimental data, even when the actual input differs significantly from a gamma distribution (see Results Section).

PKQuest Implementation: User Interface and Graphical Output

All the deconvolution procedures and the software code used in this paper are freely available on the web http://www.pkquest.com. The complete deconvolution procedure is called by a short Maple worksheet. One simple example is shown below:

sample_deconv:proc()

# The following ivinput is for a 10 minute IV infusion of 1000 micromoles ninput:1;

   ivinput[1]:table([type = 1,amount = 1000,tbeg = 0,tend = 10]);

# Venous concentration data [time, conc] resulting from above IV input:

   ivdata: [0.000,0.0000], [2.500,18.3743], [5.000,20.0258],[10.000,22.137

9], [15.000,4.1428]; [20.000,3.9987], [25.000,3.8501], [30.000,3.6699], [60.000,2.6839], [90.000,2.1099], [120.000,1.7697], [180.000,1.3768], [300.000,.9629], [480.000,.6157], [720.000,.3499]];

# Venous concentration data following an unknown input

   absdata: [0.000,0.0000], [2.500,.0001], [5.000,.0016], [10.000,.0223],[1

5.000,.0909], [20.000,.2265], [25.000,.4339], [30.000,.7055], [60.000,2.7337], [90.000,3 .6826], [120.000,3.4554], [180.000,2.2889], [300.000,1.2593], [480.000,.7631],

[720.000,.4298]];

   deconvolution:table([usedata = 3,fitfunc = 2,plotinput = 1,Nexp = 3,breakpoint = 5, scale_smooth= 1]);

   convolve(writedir,cunit,ivinput,ivdata,absdata,syspar,gammapar,gammaparmod, deconvolution);

end proc:

The amount and time course of the IV input that is used for the calculation of the bolus response function r(t) is characterized by the Maple table ivinput. The venous concentration data is described by the parameters ivdata (used to determine r(t)) and absdata (venous concentration resulting from unknown input). The data can also, optionally, be read in from a data file. The parameter deconvolution is a Maple table characterizing the type of deconvolution calculation: usedata determines whether the bolus response function, the input function, or both functions are found, fitfunc determines the deconvolution technique that is used, plotinput specifies the graphical output, Nexp is the number of exponentials in the bolus response function, breakpoint is either the type of procedure used to determine the breakpoints for the spline deconvolution, or the time interval for the uniform deconvolution and scale_smooth scales the smoothing parameter. The deconvolution procedure is run by the call to the convolve() procedure. In addition to the above parameters, a number of optional parameters can be entered: writedir is the directory where the input function is written, cunit (e.g = "micromoles") is the amount unit used in the output plots, gammapar and gammaparmod are the gamma parameter input and model function parameters and syspar is the bolus response function parameters (these 3 inputs are optional, depending on the type of calculation and graphical output). Sample deconvolution procedures and a detailed Manual and Help pages can be downloaded from the PKQuest web site.

When the above procedure is run, a large number of different graphical plots are output. The calculations of the bolus response function r(t) are routinely described by the following four plots that compare the venous concentration determined from r(t) versus the experimental data: 1)the early time points, 2) the late time points, 3) a semi-log plot of all the time points, and 4) all the time points. Three of these plots are shown in figs. 2 to 9. Three different statistical tests are applied to the r(t) calculation so that the user can determine whether a 2 or 3 exponential function should be used [32].

Figure 2.

"Simple" PBPK model with exact data sampled at high resolution. Accuracy of 2-exponential bolus input function determined using model venous concentration data generated using the "simple" PBPK organ model. The data was sampled (black squares) at the "high resolutions" time points (2.5, 5, 10, 15, 20, 25, 30, 60, 90, 120, 180, 300, 480 and 720 minutes). The left hand column shows the results for the case where a 30-second constant infusion IV infusion was used. The right hand column results are for a 10-minute constant IV infusion. The first 3 columns compare the model venous concentration (black) with the concentration determined using the bolus input function (red). The first row is for short times, the second for long times and the third is a semi-log plot for all times. The last row compares the deconvolution intestinal input rate (black) with the model input rate (green).

Figure 9.

Evaluation of the "gamma distribution" deconvolution method for "noisy" data. The green line (left column) shows the gamma distribution intestinal input to the "binding" PBPK model. The PBPK model venous concentration produced by this input was made "noisy" by adding a normally distributed random error (black squares, right column) and these data points were then used to determined an intestinal input rate (black line) and the corresponding venous concentration (red line) using the gamma distribution deconvolution method. Each row shows the results for a different set of random data.

The deconvolution calculation of the unknown input function I(t) is routinely described by the following three plots: 1) Plot of the calculated I(t) versus time, along with a comparison with the gamma distribution deconvolution (optional) and the model gamma distribution input (optional), 2) Comparison of the calculated deconvolution venous concentration with the experimental data, and 3) Plot of the total amount of absorption versus time. Examples of plots #1 and #2 are shown in figs. 9 and 10. In addition, if writedir is specified, then a text file describing I(t) is written. All of the plots shown in this paper are copied directly from the standard PKQuest output.

Figure 10.

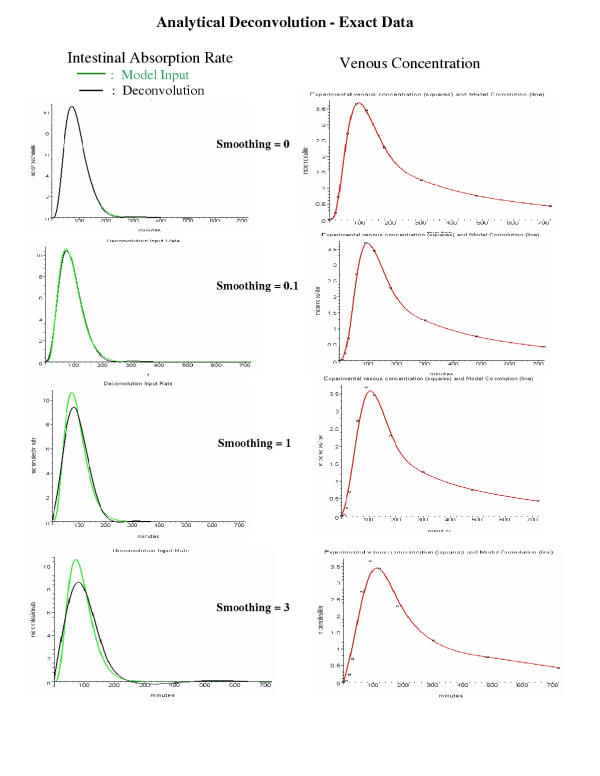
Evaluation of the "analytical" deconvolution method for exact data. Same as figure 9 except that the "analytical" deconvolution method was used and applied only to the exact venous concentration data (squares). Each row corresponds to a different analytical deconvolution smoothing parameter.

Detailed Description of Deconvolution Data Test Sets

The tests of the deconvolution procedure in this paper are based on two sets of data: one with a single gamma distribution input and one with this same gamma distribution plus a delayed, smaller gamma distribution input. In this section a detailed description of these data sets is provided so that other investigators can use this data as deconvolution test cases.

For both sets of data the system unit bolus response function was:

(6)     r(t) = 0.259e^-1.466t + 0.00188e^-0.00235t + 0.00287e^-0.0184t

The single input was a gamma distribution (eq. 2) with A= 1 mm; a = 4.85; b = 0.0534 min^-1 that started at time = 0. For the two input case a second gamma input was added with A = 0.2 mm; a = 4.85; b = 0.0269 min^-1 that started at t = 120 minutes. For the single input, the data was sampled at 10, 20,30,60,90,120,180,300,480 and 720 minutes. The exact venous concentration (micromole/liter) data for the single input at these times was: 0.0223, 0.2265, 0.7055,2.7337,3.6826, 3.4554, 2.2889, 1.2593, 0.7631, 0.4298. The corresponding data for the three noisy data sets was: Noisy #1: 0.0277, 0.1263, 0.8041, 2.7568, 3.1491, 3.9856, 2.0443, 1.2508, 0.7204, 0.3856; Noisy #2: 0.0216, 0.1794, 0.6865, 2.664, 3.643, 2.966, 1.891, 0.8765, 0.7297; Noisy #3: 0.0743, 0.1469, 0.8238, 2.6195, 4.3413, 2.9676, 2.628, 1.224, 0.8350, 0.4913. The two input data was sampled at 10, 20, 30, 60, 90, 120, 180, 240,300, 360, 420, 480 and 720 minutes. The exact venous concentration data at these times was 0.0223,0.2265,0.7055, 2.7337,3.6826, 3.455, 2.374, 1.957,1.751, 1.511, 1.270, 1.066, 0.5747. The corresponding data for the three noisy data sets was: Noisy #1: 0.029, 0.1572, 0.7951, 2.777, 3.1268, 3.9608, 2.1788, 1.981,1.567, 1.313, 1.294, 1.166, 0.6495; Noisy #2: 0.0395, 0.356, 0.6521, 2.495, 3.587, 2.9813, 2.0294, 1.4484, 1.705, 1.4749, 1.0513, 1.1566, 0.4995; Noisy #3: 0.0613, 0.1311, 0.8173, 2.6478, 4.287, 2.998, 2.721, 1.881, 1.971, 1.9528, 1.3802, 1.2038, 0.6266.

Results

Use of a gamma distribution to describe the rate of intestinal absorption

In PKQuest, a recently introduced PBPK software routine, a new approach is introduced that provides a direct measure of the rate of intestinal absorption of a solute if the PPBK parameters are known. Figure 1 shows the result of applying this technique to experimental data for three different solutes in humans: ethanol [24] (with or without a meal), standard propranolol [26] and a long acting form of propranolol [26]. The squares in these figures describe the time course of the total absorption as determined by PKQuest. The solid line is the gamma distribution fit (eq. 2) to the squares. It can be seen that in all cases the 3-parameter gamma distribution provides a good fit to the experimental data. The standard propranolol absorption rate (fig. 1, lower left panel) has a long initial time delay followed by a steep rise – a time course that is especially difficult to fit with other functions (e.g. exponential, Hill equation) but is closely fit by the gamma distribution. For this reason, the gamma distribution has been chosen in this paper as the function of choice to model intestinal absorption data. It also provides a good fit to absorption from other sites, e.g. skin, intramuscular and intraperitoneal.

Figure 1.

Gamma distribution fit to intestinal absorption rate. The absorption rates were determined by applying PKQuest to experimental measurements of venous concentrations after an oral dose of ethanol (fasting or with a meal), standard propranolol or long acting propranolol. The open squares are the experimental data points and the solid line is a 3-parameter gamma distribution fit to these points.

Use of a PBPK Model to Evaluate the Accuracy of the Determination of the Bolus Input Function r(t)

The accuracy of the determination of r(t) will be evaluated 2 different ways. In the first test, a continuous venous concentration curve will be generated using a known constant IV input to the PBPK model. This continuous curve will then be sampled at varying discrete time points which will be used to determine r(t). Comparing the venous concentration curve determined using this r(t) with the original PBPK venous data provides a direct test of the accuracy of r(t). In the second test, this r(t) will be used to calculate I(t) by applying eq. 1 to the venous concentration data produced by a known gamma distribution input to the same PBPK model. Comparison of the deconvolution I(t) versus the actual model input provides another indication of the accuracy of r(t). The model intestinal input gamma distribution parameters are similar to the absorption parameters for the standard propranolol shown in fig. 1 (A = 1 millimole; a = 4.85; b = 0.0534 min^-1).

The results will be presented for the two different PBPK models: a) the solute distributes in all the tissue water with no tissue binding (referred to as "simple" model); and b) there is tissue binding of the solute, similar to what is observed for propranolol (referred to as "binding" model) (see Methods section for a detailed description). In both models, it is assumed that the solute clearance is produced only by renal secretion and the model input is directly into a systemic vein.. Results will be shown for a 2 or 3 exponential response function for venous concentration data sampled at "high" resolution (2.5, 5, 10, 15, 20, 25, 30, 60, 90, 120, 180, 300, 480 and 720 minutes) and "low" resolution (10, 20, 30, 60, 90, 120, 180, 300, 480 and 720 minutes). The first time point for the high resolution data is at 2.5 minutes and, considering the experimental mixing and delay artifacts, one probably cannot expect to be able make accurate measurements at times before this. For each case, the results of a 10-minute constant infusion will be compared with a 30-second constant infusion. The 30-second infusion is meant to mimic an experimental "bolus" input.

Figures 2 to 8 quantitate the accuracy of the determination of the bolus response function r(t) under various conditions. In each figure, the black line is the exact model venous concentration resulting from either a 30-second (left column) or 10-minute (right column) constant IV infusion into the PBPK model system. The black squares are the discrete venous concentration data points that were used to determine r(t). The red lines in these figures are the venous concentration curves resulting from convolution of the calculated bolus response function r(t) with the model input function. The first row shows the fit for the early time points; the second row for the long time points, and the third row is a semi-log plot for all the data. The bottom row compares the true model intestinal gamma input function (green) with the intestinal input rate determined by the gamma distribution deconvolution method (see below) using this r(t) (black).

Figure 8.

"Binding" PBPK data for 30 minute constant infusion with first data point at 30 minutes.

Figures 2 and 3 show the results for the "simple" PBPK model using a 2-exponential bolus input function r(t) for the high (fig. 2) and low (fig. 3) time resolution data. For a 10-minute constant IV infusion (right column, figs. 2 and 3), the venous concentration calculated using the 2-expononential r(t) (red line) provides a good fit to the entire time course of the model venous concentration (black line). As expected for this good estimate of r(t), the deconvolution intestinal absorption rate determined using this r(t) (bottom row, black line, right column) is very close to the true, model input function (green line).

Figure 3.

"Simple" PBPK model with exact data sampled at low resolution. Same as figure 2 except the data was sampled at the "low" resolution time points (10, 20, 30, 60, 90, 120, 180, 300, 480 and 720 minutes).

For the 30-second constant infusion (left hand column) there is a sharp early spike in the venous concentration which must be fit by extrapolation of the venous data points back from the first data point at either 2.5 minutes (high resolution, fig. 2) or 10 minutes (low resolution, fig. 3). In each case, this extrapolated venous concentration (red line) is a poor approximation to the true model venous concentration (black). The bottom row in these figures quantitates the influence of this early time error on the determination of the intestinal absorption rate by deconvolution by comparing the model rate (green) versus the deconvolution rate (black). It can be seen that for this "simple" model the error in the deconvolution intestinal absorption rate is quite small, despite the large early error in the venous concentration.

Figures 4 to 8 show a similar set of results for the "binding" PBPK model. The tissue binding increases the volume of distribution and results in a more "complicated" venous concentration time course. One indication of this "complicated" times course is that a 2-exponential bolus response function r(t) no longer provides an accurate description of the venous concentration for the high resolution exact data (fig. 4, right column). In contrast, a 3-exponential r(t) provides a nearly perfect fit (fig. 6). Surprisingly, despite the poor fit to the venous data using the 2-exponential r(t) for the 10 minute infusion, the intestinal absorption rate (fig. 4, bottom row, right) determined by deconvolution using this r(t) is in good agreement with the model input (green).

Figure 4.

"Binding" PBPK model with exact data sampled at high resolution. Same as figure 2 except that the "binding" PBPK organ model was used to generate the model data.

Figure 6.

"Binding" PBPK model with exact data sampled at high resolution using 3-exponential response function. Same as figure 4 except that a 3-exponential bolus response function was used.

For the 30-second constant infusion using the binding model (left hand column, figs. 4 to 8), the venous concentration predicted using r(t) for the times preceding the first experimental time point (2.5 minutes for high resolution, 10 minutes for low resolution) differs markedly from the true, model venous concentration. The corresponding error in the intestinal absorption rate is small when the first data point is at 2.5 minutes (high resolution data, figs. 4 and 6), but becomes large when the first point is at 10 minutes (low resolution data, figs. 5 and 7).

Figure 5.

"Binding" PBPK model with exact data sampled at low resolution. Same as figure 4 except the data was sampled at the "low" resolution time points.

Figure 7.

"Binding" PBPK model with exact data sampled at low resolution using 3-exponential response function. Same as figure 6 except the data was sampled at the "low" resolution time points.

For the 10-minute constant infusion, an accurate determination of both the bolus response function and the input can be obtained when the first venous sample is at 10 minutes (fig. 7, right column). This illustrates the importance of adjusting the sample times to the IV input conditions. Figure 8 shows a similar result for a 30-minute constant infusion with the first sample point at 30 minutes. This suggests, as a general rule, that an accurate determination of the response function only requires that the first sample point be obtained at or before the end of the constant infusion.

It is clear from these results that one cannot judge the accuracy of the response function from the agreement between the model (i.e. experimental) data points (squares) and the calculated venous concentration using this response function. For example, the poorest fit to the intestinal absorption function is for the low resolution, 30-second input (fig. 5, left column), even though there is nearly perfect agreement between the data points and the predicted venous concentration using the 2-exponential r(t). The error results from the incorrect predicted venous concentrations for the times preceding the first data point at 10 minutes.

Evaluation of Deconvolution Procedures

In this section the four different techniques described in the background section will be used to determine the intestinal absorption function I(t) by deconvolution (see eq. 1). The accuracy of the different methods will be tested by the use of a known intestinal input to the PBPK model to generate the absorption venous concentration data. The I(t) determined by deconvolution of eq. 1 using this data and the previously determined bolus input function r(t) will then be compared with the actual model input. Results will be shown only for the "binding" PBPK model. The bolus input function r(t) used in this section is the 3 exponential function determined for the "binding" PBPK model using a 10 minute constant IV infusion and the high resolution venous sampling. Since this r(t) provides a nearly perfect kinetic description of this system (see fig. 6, right column), any errors in the intestinal input function I(t) must result from the deconvolution procedure. The deconvolution procedures will first be tested for an intestinal input rate described by the same gamma distribution used above for figs. 2,3,4,5,6,7,8 (gamma distribution parameters: A= 1 millimole; a = 4.85; b = 0.0534 min^-1). In order to evaluate the deconvolution methods for a more general input function that cannot be described by a single gamma distribution, the procedures will also be tested for the case where the input consists of two distinct gamma distribution, a large standard input and an additional smaller, delayed component. This input mimics the case of an intestinally absorbed solute that is excreted by the liver and then reabsorbed (enterohepatic circulation). Only the "low resolution" time points (10, 20, 30, 60, 90, 120, 180, 300, 480 and 720 minutes) will be used in this section. The "high resolution" time points used above do not improve the estimate of the absorption rate since the additional points are at early times before any significant absorption occurs. Although these "low resolution" time points are quite sparse, they are representative of the limited sampling rate that is experimentally available.

Gamma distribution Input Deconvolution

This is the approach that was used above in figs. 2,3,4,5,6,7,8 (bottom row) to determine the intestinal absorption function. As shown in those figures, when an accurate bolus response function r(t) was used (e.g. fig. 6), this method returned a nearly perfect fit to the model input function. This is not surprising since the model input was also a gamma distribution. Figure 9 shows another test of this deconvolution method using "noisy" venous concentration data. The noisy data is generated by adding random noise to each venous concentration data point (c [i], eq. 1) generated using the gamma distribution input to the "binding" PBPK model:

(7)     c[i] = c[i] + R[i] * c[i] + Noise[i]

where R [i] and Noise [i] are normally distributed random variables with a mean of 0 and standard deviations of 0.1 and 0.05 millimoles/liter, respectively. This adds a random error of 10% to each point and an additional absolute noise with a mean error of 0.05 millimoles/liter.

Each row in fig. 9 shows the results for a different set of random noisy data. The left hand column compares the deconvolution intestinal absorption rate (black line) with the model input rate (green line). The right hand column compares the corresponding deconvolution based venous concentrations (red line) with the "noisy" data points (squares) that were used to calculate the deconvolution input. The calculated intestinal absorption rate provides a good approximation to the actual input for each noisy data set. The total intestinal absorption calculation from the deconvolution varies from 0.863 (middle row) to 1.089 (bottom) compared to the actual input of 1 millimole. This approach is inherently robust since there are only 3 adjustable parameters and the shape must be a gamma distribution.

Analytical Deconvolution

In this approach, the venous concentration data are fit with a spline function, which is then used for an analytical deconvolution. The spline fit can either be an exact interpolated fit that passes through each data point, or a smoothed fit that limits the degree of curvature allowed in fitting the points (see Methods for details). This latter case is essential when fitting noisy data. In the implementation of this method in PKQuest, the user sets a "smoothing" parameter that varies from 0 (interpolating spline) to infinity. The parameter has been scaled so that, for each deconvolution method, a value of smoothing = 1 provides a good first estimate.

Figure 10 shows the result of applying this approach to the exact venous data for 4 different values of smoothing. Using an interpolating spline (smoothing = 0) provides a nearly perfect fit to the model data. For smoothing values of 1 or greater, the deconvolution results differ significantly from the model data. Despite the error in the shape of the curve, the deconvolution estimate of the total absorption remains accurate. For example, for the smoothing = 3 curve, the total calculated absorption is 1.013 compared to model input of 1 millimole.

Figure 11 shows the analytical deconvolution results using the same 3 sets of noisy data that were used in fig. 9 for the gamma input deconvolution method. Each panel in fig. 11 compares the intestinal input rate determined by this method (black) with the exact model input intestinal absorption rate (green) and the rate determined by the gamma input method in fig. 9 (red). Each column in fig. 11 is for one set of noisy data, and the results for 3 different values of the smoothing parameter are shown in the 3 rows. The "best" fits for the three sets (columns) of noisy data are for a smoothing parameter of 3 (first column), 0.1 (second column) and 1 (third column), although this choice is clearly subjective. This figure illustrates that for this method the intestinal absorption rate may have non-physical negative values. (The negative region decreases as the smoothing parameter is increased). This is one of the major limitations of this approach. The other 3 methods can be constrained (see Methods for details) to prevent this.

Figure 11.

Evaluation of the "analytical" deconvolution method for "noisy" data. Comparison of intestinal input rate determined by "analytical" deconvolution (black line), "gamma distribution" deconvolution (red line) and the PBPK model input (green line). Each column is for a different noisy data set, and each row is for a different value of the analytical deconvolution smoothing parameter.

Spline Function Input

This method uses the approach of Verotta [4,5] in which the input is parameterized by a general B-spline function and the deconvolution is obtained using a constrained regression method that prevents the input rate from having negative (non-physical) values. There are two sets of user input adjustable parameters for this method: the choice of the time "breakpoints" for the B-spline function, and the value of the smoothing parameter that "penalizes" the fits that have too sharp a curvature (see Methods for details). As was the case for the gamma distribution and analytical deconvolution techniques, this method also returns a nearly perfect fit to the model data when applied to the exact data (not shown).

Figure 12 shows the results of the application of this deconvolution method to one of the noisy data sets used in fig. 9 (first row) and fig. 11 (first column). The two columns in fig. 12 correspond to the results for two different sets of breakpoints and the different rows are for different values of the smoothing parameter. These results show the critical dependence of this method on the choice of time points used for the breakpoints. The excellent fit on the left uses breakpoints at 0, 14, 42, 68, 115,173, 290, 400 and 720 minutes. The poor fit on the right has 2 additional breakpoints, at 90 and 140 minutes.

Figure 12.

Importance of choice of "breakpoints" on "spline function" deconvolution. Comparison of intestinal absorption rate determined by the "spline function" deconvolution method (black line) with the PBPK model input (red line) for one set of "noisy" data. The two columns correspond to different sets of B-spline "breakpoints" and the rows are for different value of the spline deconvolution smoothing parameter.

The choice of time points for the good fit in the left column of fig. 12 is based on the application of the new approach introduced here. If one knows, a priori, that the absorption rate approximates a gamma distribution, then the spline break points can be chosen to provide an optimal fit to this gamma distribution (see Methods for details). In the implementation of the spline function approach in PKQuest, there are a number of options for choosing the breakpoints. One of these options is based on first finding the gamma distribution approximation to the intestinal absorption (fig. 9) and then using this function to select the break points.

The left hand column in fig. 12 also illustrates that, if this optimal set of breakpoints is used, the quality of the fit is relatively independent of the value chosen for the smoothing parameter. This is a major advantage of this approach because it means that an accurate estimate of the intestinal absorption can be obtained using the default set of parameters, without any subjective user decisions.

Figure 13 shows the fit using this default set of breakpoints (using the gamma distribution approximation) and smoothing parameter ( = 1) for the same 3 noisy data sets that were used for the analytical (fig. 9) and spline function (fig. 11) deconvolution methods. The intestinal absorption rate determined using this approach is as good as the gamma distribution approach. This may not surprising since the gamma distribution has been used to choose the break points. A better test of this approach to choosing the breakpoints is described below where an input that is clearly not a gamma distribution is used.

Figure 13.

Evaluation of the "spline function" deconvolution method for "noisy" data. Same as figure 9 except that the "spline function" deconvolution method was used. The "default" breakpoints and smoothing parameters were used for each noisy data set (rows). The red line (left column) is the gamma distribution deconvolution rate and is identical to the black line in fig. 9.

Uniform Input

In this approach the intestinal absorption function is determined on a uniform, dense sequence of time points and the stochastic regularization procedure of Nicolao et. al. [1] and Sparacino et. al. [22,23] is used for the deconvolution. This approach also constrains the solution so that the input rate cannot be negative. In this approach one solves for the concentration at many more time points then there are data points and the system is highly underdetermined. The system becomes solvable by adding a constraint on the smoothness ("regularization") of the solution. This means that the solution is strongly dependent on the user input "smoothing parameter" which can vary over a wide range depending on the time interval, number of points and experimental data. This is the main limitation of this approach. De Nicolao et. al. [1] have discussed several different criterion for choosing the "best" value of this parameter. These criteria are quite CPU intensive because they involve the repeated determination of the fits for a large number of different values of the "smoothing parameter" and then using statistical tests to select the "best" value. In this paper a new, simpler, approach is used to estimate the value of this smoothing parameter, again based on the assumption that the intestinal absorption rate can be approximated by a gamma distribution (see Methods for details). Another user adjustable parameter for this method is the unit time interval tdel (the corresponding time points where the solution is obtained are at 0, tdel, 2*tdel, 3*tdel....). There are several constraints on the choice of tdel. This interval should be a common divisor of all the experimental time points, so that the experimental points fall on the uniform time grid. The implementation in PKQuest rounds the experimental points to the nearest uniform point and, if the rounding only amounts to a few percent, the error will be negligible. The other constraint on the time points is that the CPU time for the constrained, non-negative, solution in the PKQuest implementation scales roughly as the square of the number of time points and, thus, CPU time constraints limit the size of the time interval. Since solute absorption is, in general, a slowly varying and smooth process, relatively long time intervals can be used and this latter constraint is not usually limiting.

Figure 14 shows the intestinal absorption rate determined with this approach for the exact data and the same 3 noisy data sets that were used in figs. 9, 11 and 13. (A time interval of 5 minutes was used for these results). The values of the intestinal absorption rate determined by this method at the uniform set of time points (open squares) is compared with the model input (green) and gamma distribution deconvolution result (red). All the fits use the default smoothing parameter determined from the gamma distribution fit to this same data (fig. 9). Although the fit is very good for the exact data using this default smoothing parameter, a better (nearly perfect) fit to the model rate is obtained (not shown) using a smaller (1/10) smoothing parameter. For the 3 noisy data sets, the default value corresponds to the "best" fit. Although the intestinal absorption rate determined with this method for the first noisy data set is slightly worse than the other methods, the fits for the other 2 noisy sets is as good, or better, than the other methods (compare figs. 9, 11 and 13).

Figure 14.

Evaluation of the "uniform" deconvolution method for "noisy" data. Same as figure 11 except that the "uniform" deconvolution method was used.

Two Component Intestinal Input – Comparison of Different Deconvolution Methods

In this section a more complicated model intestinal input function is used in which a small delayed component is added to the major component. The major component is started at zero time and is a gamma distribution that is identical to that used in figs. 9,10,11,12,13,14 (A = 1 mm; a = 4.85; b= 0.0534 min^-1). The second component is a gamma distribution that has parameters: A= 0.2 millimoles; a = 4.85; b= 0.0269 min^-1 and that begins at time = 120 minutes. This second component has a total input of 0.2 millimoles, 20 % of the major input, and a time course that is spread over twice the time of the major input. The venous concentration for this 2 input case is sampled at three additional time points (at 240, 360 and 420 minutes) in order to resolve the delayed absorption (time points = 10, 20, 30, 60, 90, 120, 180, 240,300, 360, 420, 480 and 720 minutes). This input mimics the situation of an orally administered drug that is excreted by the liver and then reabsorbed. The ability of the deconvolution techniques to identify this second component using noisy data presents a difficult challenge.

Figure 15 compares the deconvolution calculation of the intestinal absorption (black) versus the actual model input (green) for the four deconvolution methods using the exact venous concentration data. The "gamma distribution" fit is poor because it assumes that the input can be described by a single gamma distribution. The fits for the other 3 methods are very good. The "spline function" (bottom row, left) and "uniform" (bottom row, right) deconvolution methods use the default input parameters (smoothing and breakpoints) determined using the gamma distribution fit to this data (top row, left) (see Methods). As described above, for the analytical approach the smoothing parameter must be adjusted by the user for each experimental situation to determine the "best" fit. In fig. 18, for this exact data, a smoothing parameter = 0 is used, corresponding to the interpolating spline fit. The total amount of absorption determined using the 4 methods is (actual input = 1.2): gamma distribution, 1.16; analytical, 1.203; spline, 1.204; and uniform, 1.199.

Figure 15.

Evaluation of deconvolution methods for two component intestinal input with exact data. The green line is the composite intestinal input to the PBPK model consisting of the same gamma input used in figs. 9 to 14, plus a second, smaller, delayed gamma input. The black line is the intestinal input determined by application of the four deconvolution methods to the exact venous concentration data. The "spline" and "uniform" deconvolution methods use the "default" input parameters and the "analytical" method uses a smoothing parameter of 0.

Each column in figure 16 compares the results of the 3 general deconvolution methods applied to same 3 sets of "noisy" data (rows). As before, the noisy data is generated by applying eq. (7) to each exact venous data point c [i], with R [i] and Noise [i] normally distributed random variables with a mean of 0 and standard deviations of 0.1 (corresponding to 10% of the absolute value) and 0.05 millimoles/liter, respectively. For the results in this figure it is assumed that the user has no a priori information about the correct value and, therefore, is required to use the previously determined default values for the user input parameters. For the analytical deconvolution, this is a smoothing parameter of 1. For the spline and uniform methods, this corresponds to the default value determined (see Methods) using the gamma input function for this same noisy data set. All 3 methods indicate, qualitatively, that there is a second component. Overall, the spline function method seems to be superior, at least for inputs with this time course.

Figure 16.

Evaluation of deconvolution methods for two component intestinal input with "noisy" data. Same as figure 15 except that a random error was added to the venous concentration data. Each column corresponds to a different deconvolution method and each row to a different set of "noisy" data. The default parameters were used for all 3 deconvolution methods.

Discussion and Conclusions

Use of a PBPK Model to Evaluate the Accuracy of the Bolus Input Function r(t)

For the "simple" PBPK model in which the solute distributes in all the cell water with no binding, the bolus response function is accurately described by a simple two exponential function (fig. 2). The average fractional error for the data in the right column of fig. 2 is 0.013, an error that would certainly be swamped by experimental error. This result is consistent with the fact that a 2-exponential function is used in most of the recent experimental applications of deconvolution [18,33,34]. For the more "complicated" pharmacokinetic PBPK model where there is extensive tissue binding (similar to that for propranolol), a 2-exponential function fit is no longer adequate (fig. 4, right column, average fractional error = .041) while a 3 exponential function provides a nearly perfect fit (fig. 6, right column, average fractional error = 0.0024). It is surprising that the complicated 11-compartment PBPK pharmacokinetics can be fit with this degree of accuracy using a 2 or 3-exponential function.

Although it seems obvious that one should try to make the venous concentration measurements as early as possible in order to accurately determine the bolus response function, the results shown in figs. 2,3,4,5,6,7,8 provide the first quantitative analysis of this relationship. Based on the results for the 10 minute (fig. 7, right column) and 30 minute (fig. 8) constant infusion, the following simple rule can be inferred: an accurate determination of the response function requires that the first sample point be obtained at or before the end of the constant infusion. Intuitively, one might assume that a true bolus IV injection should provide the best estimate of the bolus response function. However, this is not correct because of the unavoidable circulatory and mixing and time delays which make venous concentration measurements for time points earlier than 2 or 3 minutes unreliable. For this reason, a relatively long constant infusion (e.g. 10 minutes) is superior to a bolus infusion. This is best illustrated by comparing the left hand column if fig. 6 with the right hand column in fig. 7: the 30-second infusion with the first data point as early as 2.5 minutes does not provide as accurate an estimate of r(t) as the 10-minute infusion with the first data point at 10 minutes.

In the experimental application of the deconvolution method it is a common procedure to evaluate the accuracy of the bolus response function r(t) by comparing the venous concentration determined from r(t) with the actual experimental venous concentration data. This analysis shows that this may not be a reliable procedure. For example, as shown in the left column of fig. 7, there is a large error in the bolus response function (and the corresponding calculation of the input function) determined using the 30-second input even though the response function provides a nearly perfect fit to the discrete model data. This error results from the very poor fit to the venous concentration at times preceding the first data point at 10 minutes.

Comparison of the Four Deconvolution Methods

Figures 9,10,11,12,13,14,15,16 quantitatively compare the accuracy of the intestinal input determined by deconvolution with the actual model input. Any differences in these two input rates must be the result of errors in the deconvolution process since the bolus response function that is used in these calculations provides a nearly perfect description of the system pharmacokinetics (see fig. 6, right column). As shown in fig. 1, the 3-parameter gamma distribution provides a versatile and accurate description of a number of different intestinal input functions. One would expect that, in most cases, intestinal absorption (and absorption from skin, intramuscular and intraperitoneal) could be approximated by a gamma distribution. For these cases the gamma distribution deconvolution is obviously the method of choice because it has only 3 adjustable parameters and the fitting process averages out most of the error in "noisy" data (fig. 9). Another major advantage of the gamma distribution approach is that there are no user adjustable input parameters (e.g. smoothing parameter), eliminating any user bias.

If the input cannot be described by a single gamma distribution then one of the other three, more general, deconvolution approaches must be used (i.e. "analytical", "spline" and "uniform"). All three of these methods can, potentially, provide a nearly perfect fit to the absorption rate if the exact venous concentration data is used (figs. 10, 12, 14). An important qualification of this statement is that this nearly perfect fit depends on the right choice of the user input parameters. All 3 methods are dependent on the "smoothing" parameter that limits the "roughness" of the absorption rate. In addition, the "spline" deconvolution method is strongly dependent on the choice of "breakpoints" (see fig. 12). An important criterion for evaluating the different methods is whether the "best" value of the parameters can be determined objectively, without any user bias. Verotta [4] and De Nicolao et. al. [1] discuss a number of different criteria for choosing these parameters, including the Akaike criterion [35] and the "Generalized Cross Validation" [36]. However, all of these criteria are semi-empirical and the different criteria yield different "best" values. In addition, in order to apply these criteria, the deconvolutions must be run many times, greatly increasing the time of the calculations.

A new approach for determining these user parameters for the "spline" and "uniform" deconvolution methods is introduced in this paper. A "default" set of parameters is determined without any user input, based on the assumption that the input function can be roughly approximated by a gamma distribution. This new approach works well for the single gamma distribution input case, with these "default" parameters providing "best" fits for both the exact and noisy data sets (figs. 14,15,16). It is, perhaps, not surprising that it works for this case since the input is close to a gamma distribution. A more discriminating test of this approach is for the two input case, when a second, smaller, delayed gamma distribution is added. Although this input differs significantly from a single gamma input (fig. 18, top left) this approach for choosing the input parameters still provided good fits for the exact (fig. 15) and noisy (fig. 16) data sets for the "spline" and "uniform" approach. Of course, if the input function has no relation to a gamma distribution, one would expect this method to breakdown. However, most physiological intestinal, skin, intramuscular or intraperitoneal absorption processes should resemble a gamma distribution and this method should be applicable.

As discussed in the background section, the "analytical" deconvolution method of Veng-Pedersen [6] is the most commonly used experimental approach. It has the advantage that is the fastest of the different methods and for exact data it provides a good estimate of the absorption rate (fig. 10). However, this method has 2 major handicaps. The first is that it is strongly dependent on the value chosen for the "smoothing" parameter and there is no direct technique that can be used to objectively determine this parameter. Even knowing the standard deviation of the experimental data (which is rarely the case) is not enough to determine the "best" value of this parameter. As shown in fig 11 for three different sets of noisy data, all generated using the same random error parameters (eq. (7)), the "best" fit has smoothing parameters varying from 0.1 (middle column) to 3 (left column). The second problem is that for the noisy data sets tested here (fig. 11) this method provides fits to the absorption rate that, subjectively, seem inferior to those determined by the other two general deconvolution approaches ("spline" and "uniform"). Also, unlike the other approaches, the analytical approach cannot be constrained from reaching non-physical negative values for the absorption rate (fig. 11).

Comprehensive quantitative evaluations of different deconvolution approaches have been described previously [7,11,22]. The evaluation in this paper is not comprehensive, using a single typical human bolus response function and just two different input functions (one and two component) that are representative of human intestinal absorption rates. For this reason, the above conclusions about the relative merits of the different methods are quite limited. A major advantage of having the four methods and the PBPK model available in a single, user friendly, software package is that it allows other investigators to carry out similar evaluations using their particular input and response functions.

All of the procedures described in the paper are implemented in PKQuest (freely distributed at http://www.pkquest.com). This software routine has a simple user interface and the output is displayed in a series of graphical plots, some of which are illustrated by the figures in this paper.

Pre-publication history

The pre-publication history for this paper can be accessed here:

http://www.biomedcentral.com/1472-6904/3/1/prepub