Probing polymerization forces by using actin-propelled lipid vesicles

Abstract

Actin polymerization provides a powerful propulsion force for numerous types of cell motility. Although tremendous progress has been made in identifying the biochemical components necessary for actin-based motility, the precise biophysical mechanisms of force generation remain unclear. To probe the polymerization forces quantitatively, we introduce an experimental system in which lipid vesicles coated with the Listeria monocytogenes virulence factor ActA are propelled by actin polymerization. The polymerization forces cause significant deformations of the vesicle. We have used these deformations to obtain a spatially resolved measure of the forces exerted on the membrane using a model based on the competition between osmotic pressure and membrane stretching. Our results indicate that actin exerts retractile or propulsive forces depending on the local membrane curvature and that the membrane is strongly bound to the actin gel. These results are consistent with the observed dynamics. After a slow elongation of the vesicle from a spherical shape, the strong bonds between the actin gel and the membrane rupture if the retractile forces exceed a critical value, leading to a rapid release of the vesicle's trailing edge.

Elongation of protein polymers by successive addition of monomeric subunits is a form of movement that is observed in a variety of biological systems (1). The building block of the most extensively explored polymerization engine is the cytoskeletal protein actin. Eukaryotic cells change shape and move by polymerizing actin at the leading edge of lamellipodia and filopodia (2, 3). The rocketing of endocytic vesicles after being pinched off from the plasma membrane (4) and the propulsion of vesicles in Xenopus oocytes and extracts require actin-based machinery (5, 6). Several pathogenic bacteria such as Listeria monocytogenes and Shigella flexneri recruit the host cell's actin to propel themselves through the cytoplasm.

Studies on actin-based motility of bacterial pathogens (7, 8) have greatly advanced our knowledge of the biomolecular basis of eukaryotic cell motility. The Listeria transmembrane protein ActA, which is distributed asymmetrically on the bacterial surface, is the only bacterial protein essential for motility (9). ActA activates the host's Arp2/3 protein complex, which nucleates actin polymerization at the bacterial surface (10) and multiplies filaments by branching (11–13). Moving bacteria are associated with a “comet tail” consisting of actin filaments crosslinked together to form a dense cylindrical gel (14). Recently, the necessary biochemical components for actin-based motility of Listeria and Shigella were identified, and motility was reconstituted in vitro by using purified proteins (15).

Despite many advances in identifying the biochemical basis of actin-dependent motion (16, 17), the precise mechanisms of force generation remain unclear. How individual actin filaments cooperatively generate large forces leading to motion and deformation is not understood. In particular, the link between microscopic theories, which describe actin polymerization as a Brownian ratchet (18–20), and macroscopic models that consider stresses arising in the entire actin gel (21) is missing. Revealing the complete mechanism requires quantitative experiments that directly probe the forces arising from actin polymerization. Biophysical studies on actin polymerization were facilitated greatly by the development of in vitro systems that explore actin-driven motility of nonbiological cargo such as protein-coated beads (22–25). However, the shapes of rigid beads are insensitive to spatial and temporal changes in the forces exerted by the actin gel.

Here we introduce an experimental system in which synthetic phospholipid vesicles containing a fraction of ActA-conjugated lipids are propelled by actin. This system has several advantages with respect to the bead assays. The vesicle membrane more closely resembles the plasma membrane of protruding lamellipodia and filopodia. Further, the lipid-membrane composition can be controlled precisely, and membrane-associated proteins are free to diffuse in the membrane. Most importantly, the vesicles can be used to measure forces due to actin polymerization. The vesicle membrane, being mechanically flexible, can deform significantly because of the strong forces arising from actin polymerization. Changes in vesicle shape reflect changes in the forces generated by the polymerizing actin gel, and vesicles thus can be used as sensitive spatial and temporal force sensors. Here we characterize the spatial distribution and temporal dynamics of actin-based polymerization forces exerted on a phospholipid membrane.

Materials and Methods

ActA Purification and Labeling.

ActA-His was purified from L. monocytogenes strain DP-L2723 (a kind gift of Daniel Portnoy, University of California, Berkeley) expressing a truncated actA gene encoding amino acids 1–613 with a COOH-terminal six-histidine tag replacing the transmembrane domain (10). A single colony of DP-L2723 was inoculated in 50 ml of Luria–Bertani (LB) broth with 50 μg/ml chloramphenicol, grown at 37°C for 6 h, then transferred to 1 liter of LB broth with 10 μg/ml chloramphenicol, and grown overnight at 37°C. After 16 h the cells were pelleted by centrifugation. Protein in the supernatant was precipitated with ammonium sulfate to 50% saturation and after centrifugation resuspended in assay buffer (20 mM Hepes, pH 7.4/100 mM KCl/1 mM MgCl₂) with 1 mM DTT/1 mM PMSF/1 mM benzamidine. After a second centrifugation at 3,500 × g for 15 min, the supernatant containing ActA-His was sterilized by filtration and stored at −80°C. Fluorescently labeled ActA-His was prepared from L. monocytogenes strain DP-L4363 (a kind gift of Peter Lauer and Daniel Portnoy, University of California, Berkeley) expressing the truncated actA-His gene containing an additional cysteine amino acid. ActA-His-Cys was purified as described above and conjugated to fluorescein-5-maleimide (Molecular Probes). The dye was dissolved in DMSO at a concentration of 10 mM. ActA-His-Cys at 0.5 mg/ml was incubated with an excess of fluorescein-5-maleimide for 1 h at room temperature. After completion of the reaction, the unbound fluorescent dye was removed by gel filtration using a Sephadex G-25 column (Molecular Probes).

Formation of Vesicles.

A mixture of 90% egg phosphatidylcholine lipids (Avanti Polar Lipids) and 10% nickel-chelating lipids (1,2-dioleoyl-sn-glycero-3-{[N(5-amino-1-carboxypentyl)iminodiacetic acid]succinyl}, Avanti Polar Lipids) dissolved in chloroform was evaporated on the inner surface of a round-bottom glass flask. For experiments with fluorescent lipids, 0.5% Oregon green-labeled lipids (1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine, Molecular Probes) were added to the mixture. The flask with the dried lipid layer was placed in a vacuum dessicator for several hours. Vesicle formation was initiated by rehydration with assay buffer. The crude vesicle suspension, containing large clumps of lipids and smaller vesicles, was spun at 1,000 × g for 1 min, and the supernatant (consisting of smaller vesicles) was used for labeling with ActA. Equal volumes of vesicle suspension and ActA stock were incubated for 1 h at room temperature while shaking and then transferred to ice. For each experiment, new lipids were rehydrated and coated with ActA before use.

Motility Assays.

ActA-coated lipid vesicles (0.5 μl) were mixed with 5 μl of bovine brain extract, 0.5 μl of purified Arp2/3 complex (at a concentration of 450 μg/ml; kind gifts of Bill Brieher, Harvard Medical School, Boston), 5 μl of assay buffer containing 2 mM ATP, 0.5 μl of ATP regenerating mix (150 mM creatine phosphate/20 mM ATP/2 mM EGTA/20 mM MgCl₂), 0.3 μl of antiphotobleach solution (0.05 mg/ml catalase/0.1 mg/ml glucose oxidase/2.5 mg/ml glucose), and 0.5 μl of monomeric actin (1:50 rhodamine-labeled, Cytoskeleton, Denver). Five microliters of the mixed sample was placed between a glass slide and a 22-mm square coverslip. The spacing between the coverslip and slide was ≈10 μm, ensuring that the motion of the observed vesicles was not constrained by the observation chamber. Observations were made on a Nikon Eclipse TE 300 inverted microscope using phase contrast and epifluorescence with a ×100 objective (numerical aperture, 1.4). Images were captured by using a cooled charge-coupled device camera (Princeton Instruments, Trenton, NJ) and analyzed with METAMORPH (Universal Imaging, Media, PA) software and MATLAB (Mathworks, Natick, MA).

Results

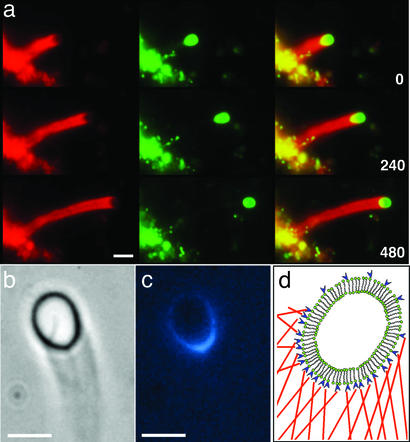
ActA-conjugated lipid vesicles are introduced into a motility assay containing rhodamine-labeled actin monomers and cytoplasmic extract from bovine brain supplemented with the Arp2/3 complex. Once added to the motility assay, the vesicles aggregate into large structures typically 10–50 μm in diameter. After a few minutes of incubation, vesicles (1–6 μm in diameter) are pinched off from the aggregates. Remarkably, these vesicles spontaneously achieve a persistent unidirectional motion. Propelled by actin polymerization, the vesicles move with velocities of 0.8 ± 0.2 μm/min, leaving curved Listeria-like actin comet tails (up to 100 μm in length) in their wake (Fig. 1a). The measured velocities of Listeria in identical motility assays are 1.9 ± 0.3 μm/min. The actin filaments are observed to form a cup that encloses only one hemisphere of the vesicle. To determine the distribution of ActA on the vesicle surface, we used fluorescently labeled ActA to coat the lipid vesicles. After motility is initiated, the spatial distribution of ActA is highly polarized and closely correlated with the position of the actin cup in the moving vesicle, as seen from phase-contrast and fluorescence images (Fig. 1 b and c). As the actin cup changes shape and orientation around the vesicle, we observe that ActA redistributes itself to always remain colocalized with the actin. Because the phospholipid bilayer is a two-dimensional fluid, a homogenous ActA distribution would be expected based on diffusion of the ActA-conjugated lipids. However, the experimentally observed polarization indicates an affinity between ActA and actin filaments. Fig. 1d shows a schematic of the three main structural ingredients of our vesicle-motility system: the lipid bilayer vesicle, ActA molecules, and actin filaments. Vesicles displayed motile behavior only when the concentration of chelating lipids was ≈10%. For larger (50%) or smaller (2%) concentration, no motility was observed. Use of synthetic lipids such as 1,2-dioleoyl-sn-glycero-3-phosphocholine did not change the motility characteristics of the vesicles.

Figure 1.

Actin-driven motility of lipid vesicles coated with ActA. (a) Fluorescence images of an actin-propelled vesicle at three time points. A fraction of the lipids (0.5%) was labeled with Oregon green. Actin was labeled (2%) with rhodamine (red). (Left) Fluorescence images of actin comet tails. (Center) Lipid fluorescence. (Right) Overlay of Left and Center. Parts of the lipid structures containing both lipids and actin appear yellow in the images. The yellow region on the vesicle clearly shows the actin “cup” enclosing one hemisphere of the vesicle. The bottom left shows the lipid aggregate from which the vesicle emerged. Time is indicated in seconds in the bottom right corners. (b) Phase-contrast image of a moving vesicle with a phase-dense comet tail. (c) Fluorescence image of the same vesicle as shown in b with fluorescently labeled ActA molecules (blue). ActA is colocalized with the actin cup on the vesicle surface. (d) Schematic diagram of a lipid bilayer vesicle (green) coated with ActA (blue) and surrounded by a mesh of actin filaments (red) in contact with the membrane. (Scale bars, 4 μm.)

The forces required to deform a unilamellar vesicle from its rest shape are determined by the energies required to bend and stretch the membrane and change the volume of the vesicle against an osmotic pressure. The bending energy is several orders of magnitude smaller than the latter two and therefore can be neglected (26). We observe that vesicles deform significantly from a quasispherical shape to a more elongated shape in response to actin polymerization. As the vesicle deforms, its surface stretches, setting up a membrane tension that induces stresses pulling the membrane inward to restore its original area. Simultaneously, an outward osmotic pressure develops due to a decrease in volume. The total stress is the sum of the osmotic pressure and the stress induced by stretching. The area and volume changes and the corresponding stresses must be in opposite directions if the vesicle is not to collapse. The front of the vesicle, which is not in contact with actin, assumes a spherical shape that minimizes the total energy. Here, the osmotic pressure and the stress due to membrane stretching balance. At any other point, the total stress is balanced by the stress due to actin polymerization. This leads to the simple result that the local stress is the product of the tension and the curvature difference between the actin-free region and any other point on the vesicle surface (see Estimation of Stress Distribution). Therefore, an analysis of the curvatures provides important information regarding the stress distribution.

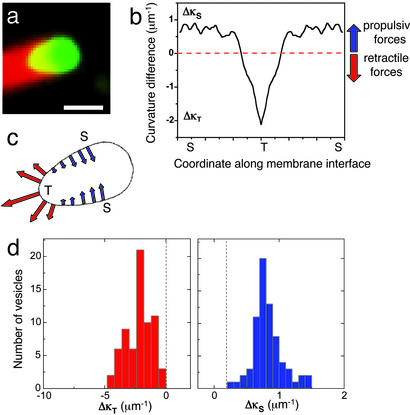
Fig. 2a shows the fluorescence image of a vesicle deformed into a typical “teardrop” shape (t = 240 sec; Fig. 1a). We analyzed the shape of this vesicle to obtain the curvature differences along its surface as shown in Fig. 2b. The curvature difference can be both positive and negative, resulting in inward and outward stresses at the surface. Fig. 2c shows a schematic representation of the forces on the surface of the vesicle shown in Fig. 2a. We find that the actin-induced stresses can be both retractile (actin pulls the membrane at the trailing part of the vesicle) and protrusive (actin pushes the membrane at the vesicle sides). The pulling stress is highest in regions of greatest curvature, as depicted by the large arrow at the trailing edge of the vesicle. Fig. 2d shows histograms of the curvature difference Δκ between the actin–membrane interface along the vesicle and the spherical cap for 50 deformed vesicle shapes. We find that this difference is always positive (squeezing) at the vesicle sides and negative (retractile) at the trailing end. Although we do not have an accurate measure for the area and volume changes of the vesicle and hence the membrane tension, we can use the curvature analysis to obtain an upper bound for the stresses and get an order of magnitude estimate for the range of these stresses for various vesicle shapes. The maximum tension that can be supported by typical bilayer membranes is on the order of 3–4 mN/m for 2–3% area increase (27). Consequently, based on the curvature differences, the maximum pulling stresses are on the order of 6–8 nN/μm², and squeezing stresses are on the order of 3–4 nN/μm².

Figure 2.

Spatial distribution of forces on a deformed vesicle. (a) Fluorescence image of the typical teardrop shape assumed by a moving vesicle deformed by actin. The color scheme is the same as described for Fig. 1. (Scale bar, 3 μm.) (b) Plot of the curvature difference between the spherical cap and a point on the vesicle surface as a function of the spatial coordinate along the vesicle surface. T and S denote the tip of the trailing edge and the sides of the vesicle, respectively. The curvature difference goes from a maximum negative value at the trailing end Δκ_T to a smaller positive value Δκ_S at the sides. The noisy appearance of the curvature profile is due to numerical estimation from a digitized image. (c) Contour of the vesicle, the curvature of which is shown in b. The arrows represent the stress at the membrane–actin interface; the relative sizes of the arrows are proportional to the magnitudes of the curvature difference, and the direction of the arrows indicates the direction of the stress experienced. (d) Histograms showing the maximum positive and negative curvature differences occurring on the tip of the trailing end and the vesicle sides, respectively, of 50 deformed vesicle shapes.

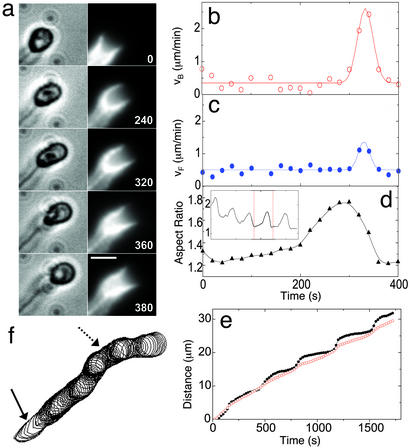
The above analysis gives a description of the spatial distribution of stresses at the membrane–actin interface of a deformed vesicle at any time instant. Observation of the moving vesicles over time shows that the vesicles exhibit dramatic shape changes as they move, indicating that the external forces causing the deformations are not constant. Fig. 3a shows successive images of a vesicle that elongates from an initially quasispherical shape and then returns to a more spherical shape. The trailing end of the vesicle in contact with the actin gel appears to be released from the cup immediately after reaching maximum deformation. Both ends move at a steady velocity of ≈0.4 μm/min between t = 0 and 300 s (Fig. 3 b and c). During this period the vesicle slowly evolves from a quasisphere with an aspect ratio of ≈1.2 to a significantly elongated shape (aspect ratio = 1.7; Fig. 3d). The elongation of the vesicle is accompanied by an increase in the actin-cup surface area as the polymerizing actin creeps around the membrane. Between t = 300 and 360 s, the vesicle returns to its spherical shape. The trailing end snaps forward at a speed of 2.5 μm/min (Fig. 3b) (six times faster than its initial velocity), indicating that the vesicle membrane is released from the actin gel. These observations, along with the fact that there is a retractile force at the trailing end, suggest that the membrane is bound to the actin gel. The elongation-and-release process can occur several times in succession, resulting in a distinct stepping motility of the vesicles as illustrated in Fig. 3 d Inset and e. The trailing end of the vesicle moves in steps (indicating a release from the actin cup), whereas the leading end moves more smoothly. The step-like motion is clearly visible in the overlay of vesicle contours at successive time steps (Fig. 3f). The typical stepping time is on the order of 5 min, and the step size is on the order of the vesicle diameter (2 μm).

Figure 3.

Dynamics of the elongation and release of a vesicle from the actin gel. (a) Time sequence of phase-contrast (Left) and fluorescence (Right) images of a vesicle going through a slow-elongation and rapid-release phase. Phase-contrast images show the vesicle and a trailing comet tail. Fluorescence images show the intensity of rhodamine-actin in gray scale. The actin cup elongates from an initial shallow shape and creeps around the vesicle, becoming shallow again as the vesicle appears to be released suddenly from the cup and becomes spherical. The time elapsed in seconds is shown on the bottom right corner of the fluorescence images. (Scale bar, 3 μm.) (b and c) Instantaneous velocity of the back (V_B) and front (V_F) of the moving vesicle as a function of time. Time-lapse images acquired at intervals of 20 sec were used to quantify the velocity and shapes. The solid lines are a guide to the eye. (d) Aspect ratio of vesicle shape as a function of time. Aspect ratio is defined as the maximum length divided by the maximum width perpendicular to the length. The highest velocity occurs just after the vesicle reaches its maximum length. (Inset) Aspect ratio of a vesicle that repeats the elongation–relaxation cycle several times. The vertical dotted lines indicate the part of the time series that is shown in greater detail in d. (e) The distance traveled by the front (open circles) and back (filled circles) of a stepping vesicle, as a function of time. (f) Overlay of vesicle contours from phase-contrast images at successive time steps (20-sec intervals) of motion, showing oscillations in velocity. In regions where the contours are further apart (solid arrow), the trailing edge of the vesicle moves rapidly; regions of densely packed contour lines (dashed arrow) depict slower forward motion during vesicle elongation.

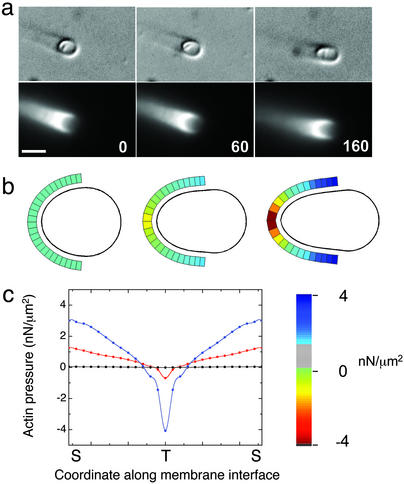
To follow the time evolution of vesicle shapes, we incorporated the dynamics of actin polymerization in a simple model of vesicle deformation (see Vesicle-Deformation Model for details). The model consists of an axisymmetric vesicle of quasispherical shape represented as a discretized closed curve. Part of the vesicle consists of points representing actin filaments in contact with the surface. The stresses at the actin–membrane interface can be estimated by comparing the deformed vesicle shape to its rest shape. The vesicle shape evolves from the rest shape as each point on the actin-covered section is moved perpendicular to the membrane, reflecting the addition of actin monomers. The local polymerization rate is a function of the local stress. As the vesicle deforms due to actin polymerization, it develops a membrane tension and osmotic pressure as described before. The total local stress is the sum of the osmotic pressure and the stress induced by stretching. The front portion of the vesicle, which is not in contact with actin, is allowed to assume a spherical shape that minimizes the total energy. The actin-covered points are then redistributed such that they cover half of the actin-free region to account for the experimentally observed “creeping” of the actin cup around the vesicle. Fig. 4a shows the experimental time series of a vesicle as it goes from an initially spherical shape to a more elongated shape. We start the model from a shape with the same aspect ratio as in Fig. 4a Left and follow the model shapes as they change over time due to actin polymerization. The stress distribution on the vesicle surface is shown in Fig. 4b for shapes with similar aspect ratios as in Fig. 4a. The color scale indicates the value of the local stress. Note that as the vesicle deforms, it experiences larger pulling forces at its trailing end and larger squeezing forces on its sides. The directionality of the stress distribution is preserved over time, and we observed both pulling and squeezing forces at different times. The stress profiles, shown in Fig. 4c, illustrate how the stresses change from a shallower to a steeper profile as the vesicle deforms. The stress values are of the same order and within the upper bound obtained from the simple curvature analysis.

Figure 4.

Evolution of stresses on a vesicle surface. (a) Differential interference contrast microscopy and fluorescence images of a deforming vesicle as it changes shape over time. The vesicle deforms from an initial quasispherical shape to an elongated shape. The time in seconds is denoted in the bottom right corner. (Scale bar, 3 μm.) (b) Simulated contours of a deforming vesicle from the model. The local stresses as obtained from the model are indicated in color around the part of the vesicle that is in contact with actin. The color bar shows the variation of the color scale with the stress values. (c) Stress profiles along the actin–membrane interface for the three different time points shown. The blue line corresponds to the last, most deformed shape, the red line corresponds to the intermediate shape, and the black line corresponds to the original shape. T, tip of the trailing end; S, vesicle sides.

Discussion

We have used an experimental system of actin-propelled lipid vesicles to characterize the forces due to actin polymerization. Several previous studies have developed in vitro reconstituted systems using bacteria (15) and protein-coated beads (22–25) to explore the mechanisms underlying actin-based motility. Actin polymerizes on the surface of these objects into a crosslinked gel, and the force due to polymerization is sufficient to produce forward motion. Because the rigid bacteria and beads are resistant to deformation, significant elastic stresses build up in the actin gel (21). Because the stress response of the actin gel is hard to visualize, rigid loads such as bacteria or beads are not very good experimental systems for characterizing the forces arising from polymerization. In contrast, when a flexible membrane vesicle is deformed, the stresses due to polymerization cause a measurable response in the vesicle by stretching the membrane or changing the vesicle volume. Earlier studies have demonstrated the actin-driven motility of endocytic vesicles (4), endosomes and lysosomes (5), and synthetic vesicles (6). Membrane vesicles propelled by major sperm protein have also been observed in cell-free extracts (28). However, these lipid-vesicle systems were never used to measure the magnitude, direction, and distribution of the forces generated at the actin–membrane interface. Our experiments with deformable lipid vesicles provide direct visual demonstration of the distribution of actin forces on a moving load represented by the changes in vesicle shape.

Our results demonstrate that to deform a vesicle from a quasispherical shape to the elongated shapes observed experimentally, actin exerts both retractile and propulsive forces depending on the local membrane curvature. We can understand this as follows. Some of the actin filaments may be tethered to the vesicle surface, whereas others are free to polymerize. In response to the membrane stretching due to deformation, the tethered filaments exert a tensile stress on the membrane surface. We find that the average magnitude of the maximum protrusive actin pressure is in the range of a few nN/μm². For a density of a few hundred actin filaments per μm² (deduced from electron microscopy studies such as in refs. 14 and 29), each filament contributes on the order of 10 pN. The maximum retractile force is larger than the propulsive forces. The presence of a retractile force localized at the trailing edge of the vesicle implies that the membrane has to be bound to the actin-filament network. Otherwise, the teardrop-shaped vesicle would relax immediately to its spherical equilibrium shape.

Additionally, the colocalization of ActA and F-actin (Fig. 1c) indicates an affinity between the two proteins, which could be due to a direct binding between these two proteins or mediated by a third protein such as the Arp2/3 complex. This affinity is consistent with recent nanometer tracking (30), laser tweezers (31), and electron microscopy (32) experiments. However, we do not obtain an explicit measure of the strength of association between the vesicle and the actin tail, which could arise from a few strong bonds or many weak bonds. These results constrain Brownian ratchet models used to describe the microscopic polymerization mechanism (18, 19), which assume that the actin filaments are not attached to the lipid membrane. A recent extension of the Brownian ratchet model incorporates these experimental findings (20). Binding between actin and the membrane is also included in an alternate model of clamped-filament elongation (33) and a continuum model for Listeria propulsion (21).

The elongation of the vesicle, which corresponds to an increase in the retractile stresses at the trailing edge, is followed by a rapid return to a spherical shape. We propose that the relaxation occurs because the retractile force at the trailing edge of the vesicle reaches a critical value beyond which the bonds between actin and the membrane rupture. We estimate that stresses on the order of 5–10 nN/μm² are required to break the bonds, which would lead to a force of ≈10–20 pN per filament, assuming a density of filaments similar to that observed in Listeria (14, 29). After rupture, the vesicle membrane moves to its equilibrium shape at a velocity much larger than the actin-polymerization speed. This behavior is reminiscent of the hopping of a Listeria mutant (21, 34) and the stepping motion of beads (25). However, the mechanism of this motility is very different in our system, because the stress is generated mainly in the deformable membrane rather than in the actin gel.

Another key feature of our experimental system is that unidirectional motion is made possible by the reorganization of a membrane-associated protein, ActA, in contrast to beads that must undergo a symmetry-breaking event (23). Spontaneous development of polarity in vesicles is fundamentally different, because ActA is free to diffuse in the plane of the membrane. Similar mechanisms involving protein reorganization may be at work in the plasma membrane to induce unidirectional motion in a moving cell. Because actin polymerization can deform the membrane significantly, our results show that the physical properties of the membrane and its stress response may be important in determining the shape of the cell membrane. Further, the cell may alter the physical parameters of the plasma membrane, e.g., membrane tension (35), and thus regulate its dynamics.

The general phenomena deduced from our observations are likely to play an important role in actin-polymerization dynamics at the leading edge of lamellipodia and filopodia of eukaryotic cells. Spatially controlled actin polymerization is at the origin of eukaryotic cell motility. Local actin polymerization generates a directed force that pushes the cell membrane forward. Such a directed force deforms the cell membrane at the leading edge and is accompanied by large changes in cell shape. Despite the higher level of biochemical complexity in moving cells as compared with our model experimental system, the basic physical ingredients are the same: polymerizing actin filaments interacting with a deformable membrane to produce shape changes and motion. Our vesicle-motility system reveals phenomena resulting from the interplay of polymerization and membrane deformation and provides a measure of spatially resolved actin forces and their dynamics.

Appendix

Estimation of Stress Distribution.

The fractional volume change of a deformed vesicle corresponds to an osmotic pressure Π acting to push the membrane outward. The corresponding area stretching introduces a membrane tension τ that is isotropic over the surface of the vesicle because the membrane is fluid. The front portion of the vesicle that is not in contact with actin assumes a spherical shape characterized by the principal curvatures, κ₁ and κ₂. The stress σ due to stretching over the spherical cap is given by

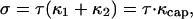where κ_cap is the total curvature that is balanced by the osmotic pressure. Therefore,

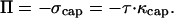This gives us a measure of the osmotic pressure in terms of the tension and the total curvature of the spherical cap. At any other point x on the vesicle surface, the total stress, which is balanced by the stress due to actin polymerization, is given by the sum of the osmotic pressure and the local tensile stress at that point.

The stress therefore is linearly proportional to the difference in curvature between the spherical cap and any other point on the vesicle surface.

Vesicle-Deformation Model.

To estimate the forces exerted by actin polymerization on the membrane we make the following assumptions. (i) Membrane bending can be ignored. (ii) Vesicles are unilamellar. (iii) In their rest state the vesicles are not stretched and have no osmotic pressure across the membrane. As the vesicles are prepared in a solution of similar ionic strength as the motility assay and assemble in the absence on any external forces on the vesicles, they will equilibrate to a nonstretched state without an osmotic pressure. (iv) Vesicles are axisymmetric spheroids of revolution.

The model considers an axisymmetric vesicle partially covered with actin filaments in contact with the surface at several points. The spacing of these points d is chosen to reflect the density of actin filaments seen in electron microscopy studies (14, 29). These filaments are assumed to be bound to the surface. The outward osmotic pressure Π of a vesicle of volume V is given by

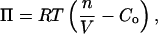where C_o is the external concentration of solute molecules impermeant to the vesicle membrane, n is the number of moles of such solutes within the vesicle, R is the ideal gas constant, and T is the absolute temperature. The osmolarity, determined by using a vapor-pressure osmometer (VAPRO 5500, Wescor, Logan, UT), was measured to be C_o = 239 ± 5 mM from eight different batches of brain extract.

For a membrane deformed from an area A_o to an area A, the area dilation α is related to the membrane tension τ by (36, 37)

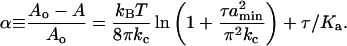We experimentally confirmed this relation for our composite egg–phosphatidylcholine/nickel-chelating lipids by using a vesicle-aspiration method (36). The relation between the membrane tension and the area dilation yields the bending modulus k_c and the stretching modulus K_a. We measured these parameters and found k_c = 9 ± 3 k_BT and K_a = 102 ± 40 mN/m (n = 14). The full data set was best fit by assuming a shortest possible wavelength of membrane undulation a_min ≈ 50 nm.

Based on the tension the total stress at the membrane–actin interface is given by the sum of the stress due to the area stretching and osmotic pressure,

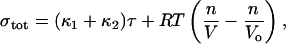where κ₁ and κ₂ are the local principal curvatures. The speed of a polymerizing gel is limited by the opposing stress (38),

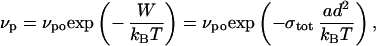where W is the work done against the opposing stress. This work is expressed as the opposing stress, integrated over the surface area per filament [d² = (25 nm)²; ref. 14] to get a force and multiplied by the distance over which a single polymerization event occurs (a = 2.7 nm, the effective actin monomer size; k_B, Boltzmann's constant). At a given time, each point on the vesicle is moved a distance dr = v_pdt perpendicular to the vesicle (v_po dt = 5 nm). The actin-covered section of the vesicle will evolve according to the polymerization speed determined by local stresses. Because the vesicle always has A > A_o and V < V_o, we cap the actin-covered section in such a way to maximize V while minimizing A. This is best realized by a spherical cap, which has the minimum energy of any accessible state. After every time step, the stress at each modeled point on the membrane is calculated. Before the next iteration, we redistribute the modeled points such that they cover half of the spherical cap. This is consistent with experimental images in that the part of the vesicle not in contact with actin resembles a hemisphere, and the actin cup is observed to creep around the vesicle as it deforms.

For multilamellar vesicles, the membrane elastic properties depend on the number of layers (39). Changing the stretching modulus of the membrane by a factor of 4 changes the maximum stresses by up to a factor of 2.0. The stress profile changes with the stretching modulus but is characterized by negative stresses at the end and positive stresses on the sides always.