Tuning of conformational preorganization in model 2′,5′- and 3′,5′-linked oligonucleotides by 3′- and 2′-O-methoxyethyl modification

Abstract

Conformational properties of trimeric and tetrameric 2′,5′-linked oligonucleotides, 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2), and their 3′,5′-linked analogs, 2′-MOE-A₃^3′,5′ (3) and 2′-MOE-A₄^3′,5′ (4), were examined with the use of heteronuclear NMR spectroscopy. The temperature-dependent ³J_HH, ³J_HP and ³J_CP coupling constants, acquired in the range of 273–343 K, gave insight into the conformation of sugar rings in terms of a two-state North ↔ South (N ↔ S) pseudorotational equilibrium and into the conformation of the sugar–phosphate backbone in the model antisense oligonucleotides 1–4. 2′,5′-linked oligomers 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2) show preference for N-type conformers and indication of A-type conformational features, which is prerequisite for antisense hybridization. The drive of N ↔ S equilibrium in 1–4 has been rationalized with the competing gauche effects of 2′/3′-phosphodiester and 3′/2′-MOE groups, anomeric and steric effects. Furthermore, the pairwise comparisons of 3′-MOE with 3′-OH and 3′-deoxy 2′,5′-linked adenine trimers emphasized the fine tuning of N ↔ S equilibrium in 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2) by the steric effects of 3′-MOE group and the possibility of water-mediated H-bonds with vicinal phosphodiester functionality. In full correspondence, the drive of N ↔ S equilibrium towards N by 2′-MOE in 3′,5′-linked analogs 2′-MOE-A₃^3′,5′ (3) and 2′-MOE-A₄^3′,5′ (4) is weaker in comparison with 3′-OH group in the corresponding ribo analogs. β^t, γ⁺ and ε^– rotamers are preferred in both 2′,5′- and in 3′,5′-linked oligonucleotides 1–4.

INTRODUCTION

The success of DNA phosphorothioates as antisense agents has stimulated a wide variety of chemical modifications in the phosphate backbone, pentofuranosyl moieties and nucleo base fragments of nucleic acids (1–4). An ideal antisense oligonucleotide is expected to favorably hybridize with RNA, exhibit cell permeability and resistance to enzymatic degradation as well as induce cleavage of the hybrid duplex by nucleases such as RNase H. All these requirements are difficult to combine in a single construct that is a candidate for potential gene-targeting applications. The second generation of antisense oligonucleotides involves the modification of a 2′-OH group with other electronegative groups that favor N-type sugar conformation through the gauche effect of [O4′-C1′-C2′-X2′] fragments (2,3). Recently, the locked nucleic acids have been introduced in which the 2′-O,4′-C-methylene bridge locks the nucleotide in a C3′-endo (N-type) conformation (5–7). The preference for N-type sugar conformation improves binding affinity (8–10). In addition, carbohydrate modifications at the 2′-position of RNA mimic increase nuclease resistance, chemical stability against depurination and alter the lipophilicity, all of which contribute to improved pharmacokinetic properties (11). For example, 2′-O-(2-methoxyethyl)-RNA [(2′-MOE)-RNA] oligonucleotides exhibit C3′-endo sugar conformation, stand out in their binding affinities to target RNAs and show good nuclease resistance (4).

Comprehensive analyses of a two-state North (N, roughly C3′-endo) ↔ South (S, roughly C2′-endo) pseudorotational equilibrium in nucleosides and nucleotides have shown that the sugar conformation is controlled by the gauche effects of [O4′-C-C-O3′/2′] fragments, anomeric effect of the heterocyclic nucleobase and steric interactions (12–17). The quantitative thermodynamic data on N ↔ S equilibrium has proved itself in the design of modifications that lead to the desired engineered major conformers of pentofuranosyl moieties, which subsequently drive sugar–phosphate backbone conformation. The more a nucleoside building block is preorganized in an N-type furanose conformation, the higher the stability of the duplex between the modified oligomer and its RNA complement (2,3). A recent NMR study has shown that DNA with 2′,5′-phosphodiester bonds forms an A-type duplex in solution (18).

In the present study we have focused on the backbone-modified 2′,5′-linked oligonucleotides (19) that have recently shown modulation of immunostimulatory properties (20). It has already been shown that antisense applications of 2′-MOE-substituted RNA oligonucleotides, with 3′,5′-linked backbones, exhibit improved nuclease resistance, higher RNA affinity, reduced toxicity and better cellular uptake in comparison with their 2′-OH analogs (4). Here we have prepared 2′,5′-linked adenosine oligonucleotides with 3′-MOE modification 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2) (Scheme 1). The conformational properties of 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2) (Scheme 1) were assessed in aqueous solution with the use of heteronuclear NMR spectroscopy and compared to their 3′,5′-linked analogs, trimer 2′-MOE-A₃^3′,5′ (3) and tetramer 2′-MOE-A₃^3′,5′ (4).

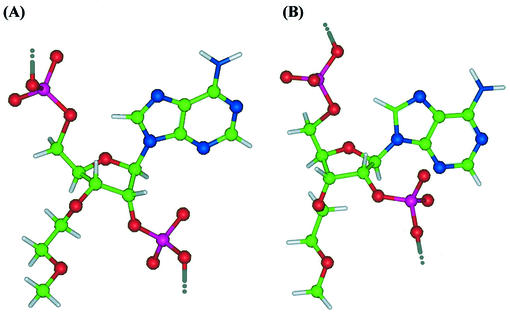
Scheme 1. (A) Non-terminal monomer building block of 2′,5′-linked trinucleoside diphosphate 3′-MOE-A₃^2′,5′ (1) and tetranucleoside triphosphate 3′-MOE-A₄^2′,5′ (2). (B) Non-terminal monomer building block of 3′,5′-linked trinucleoside diphosphate 2′-MOE-A₃^3′,5′ (3) and tetranucleoside triphosphate 2′-MOE- A₄^3′,5′ (4).

Our results show that the substitution of 3′-OH group in 2′,5′-linked oligonucleotides by 3′-MOE, as found in 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2), leads to increased populations of N-type conformers that, in addition to all the advantages of 2′-MOE modification in natural 3′,5′-linked analogs, results in conformational preorganization that offers favorable hybridization properties. In contrast, the analysis of temperature-dependent NMR data shows that 2′-MOE modification in natural 3′,5′-linked oligonucleotides, 2′-MOE-A₃^3′,5′ (3) and 2′-MOE-A₄^3′,5′ (4), leads to preferential stabilization of S-type conformers in comparison to parent ribo oligomers.

MATERIALS AND METHODS

NMR measurements

NMR spectra were recorded on Varian Unity Inova 600 NMR spectrometer at the Slovenian NMR Center at 600.07 MHz for ¹H nuclei, 150.91 MHz for ¹³C and 242.91 MHz for ³¹P nuclei. Spectra were acquired in D₂O (99.9% deuterium), 10 mM Na-phosphate buffer at neutral pH (pH* = 6.9) and 18 mM 3′-MOE-A₃^2′,5′ (1), 14 mM 3′-MOE-A₄^2′,5′ (2), 13 mM 2′-MOE-A₄^2′,5′ (3) and 11 mM 2′-MOE-A₄^2′,5′ (4). The pH* values were measured by a combined glass electrode calibrated with standard buffers with a pH of 4, 7 and 10 in H₂O and were not corrected for the deuterium isotope effect. Tetramethyl ammonium chloride was used as internal reference for ¹H NMR (δ = 3.185 p.p.m.) spectra. ³J_H1′H2′, ³J_H2′H3′, ³J_H3′H4′ and ³J_H2′P coupling constants were measured from 1D ¹H proton spectra, whereas ³J_H4′H5′, ³J_{H4′H5′′}, ³J_H5′P and ³J_H5′′P coupling constants were obtained from DQF-COSY spectra and J_CP coupling constants from HSQC spectra. The errors in coupling constants were: ±0.1 Hz for J_HH, ±0.2 Hz for J_HP and ±0.4 Hz for J_CP and J_{H5′/5′′P}. The sample temperature was varied from 273 to 343 K and controlled to approximately ±0.1 K.

1D ¹H measurements were performed under the following spectral and processing conditions: 5.4 kHz sweep width, 32 K time domain, zero filling to 128 K and slight Gaussian apodization to give enhanced resolution. J_CP coupling constants were obtained with the use of extensively folded HSQC experiments (21) using gradients for coherence selection; 4096 (ω2) × 2048 (ω1) data points, 16 scans per FID, 16 dummy scans, appropriate delays were calculated according to ¹J_CH = 140 Hz, 5.4 kHz (ω2) × 2.4 kHz (ω1) spectral width, transformed after multiplication with a sine-bell squared filter shifted by π/2 in both ω2 and ω1 to give 8 × 16 K matrix. DQF-COSY experiments were acquired with 4096 (ω2) × 1024 (ω1) data points, 16 scans per FID, transformed after multiplication with a sine-bell squared filter shifted by π/2 in both ω2 and ω1 to give 8 × 2 K matrix. NOESY experiments were acquired with 4096 (ω2) × 256 (ω1) data points, eight scans per FID, with mixing times from 100 to 400 ms. Digital resolutions were 0.05 Hz in ¹H 1D spectra, 0.2 Hz along ¹H (f2) axis of DQF-COSY spectra and 0.3 Hz along ¹³C (f1) axis of HSQC spectra.

Conformational analysis

The conformational analysis of sugar moiety has been performed with the computer program PSEUROT (22,23) with the use of λ electronegativities (24) for the substituents along H-C-C-H fragments and the six-parameter generalized Karplus–Altona equation (25). The following λ electronegativity values were used: 0.0 for H, 0.58 for heterocyclic base, 1.26 for OH, 1.25 for phosphate group, 0.62 for C1′, C2′, C3′ and C4′, 1.27 for O4′ and 0.68 for C5′. In the optimization procedure the geometries and populations of both N- and S-type pseudorotamers were varied to obtain the best fit between the experimental and the calculated coupling constants. Our optimization procedure started with the following values: P_N = 18°, Ψ_m^N = 36°, P_S = 162° and Ψ_m^S = 36°. The puckering amplitude and phase angle of the minor S-type conformer was kept frozen during the individual iterative least-squares optimization, whereas parameters for the minor N-type were freely optimized and vice versa. The optimization resulted in the following ranges of P and Ψ_m for the N- and S-type geometries in all residues which best agreed with the experimental ³J_HH coupling constant data: –7° < P_N < 19°, 146° < P_S < 158°, 34° < Ψ_m^N = Ψ_m^S < 36°, r.m.s. < 0.15 Hz, ΔJ_max < 0.23 Hz for individual residues in 3′-MOE-A₃^2′,5′ (1), –13° < P_N < 16°, 140° < P_S < 160°, 31° < Ψ_m^N = Ψ_m^S < 38°, r.m.s. < 0.15 Hz, ΔJ_max < 0.34 Hz for individual residues in 3′-MOE-A₄^2′,5′ (2), –15° < P_N < 32°, 134° < P_S < 182°, 33° < Ψ_m^N = Ψ_m^S < 39°, r.m.s. < 0.15 Hz, ΔJ_max < 0.32 Hz for individual residues in 2′-MOE-A₃^3′,5′ (3). For 2′-MOE-A₄^3′,5′ (4) we were able to measure only ³J_H1′H2′ coupling constants and thus geometries obtained for 2′-MOE-A₃^3′,5′ (3) were used in conformational analysis of individual residues in 2′-MOE-A₄^3′,5′ (4), whereas populations of individual conformers were optimized.

MD simulation

MD simulation of 3′-MOE-A₃^2′,5′ (1) was performed with Insight II (v. 2000.1) software package (Accelrys) employing the AMBER force field. Distance-dependent dielectric constant value of 4 was used and Coulombic interactions have been reduced to 0.1. Starting geometry of 3′-MOE-A₃^2′,5′ (1) was energy minimized and MD simulation was started. Simulation was performed for 3 ns at 600 K after a few preliminary short MD simulations at various temperatures from 300 to 1000 K.

RESULTS

The conformational equilibria of trimers 3′-MOE-A₃^2′,5′ (1) and 2′-MOE-A₃^3′,5′ (3), and tetramers 3′-MOE-A₄^2′,5′ (2) and 2′-MOE-A₄^3′,5′ (4) in aqueous solution were evaluated with the use of ¹H, ¹³C and ³¹P NMR spectroscopy. ¹H NMR chemical shifts were measured at 11 temperatures between 273 and 343 K (see Table 1 for data at the lowest and the highest temperatures). All proton resonances of sugar and nucleobase protons in model oligonucleotides 1–4 have been completely assigned with the use of NOESY experiments, selective 1D TOCSY and 2D DQF-COSY, ¹H-¹³C HSQC and ¹H-¹³C HMBC experiments. The 2′/3′- and 5′-terminal residues in 1–4 were easily identified due to the absence of scalar coupling of respective protons with phosphorous atoms. The temperature-dependent vicinal ³J_HH, ³J_HP and ³J_CP coupling constants (Table 2), and NOE enhancements reflected time-averaged values of several rapidly interconverting conformers in aqueous solution.

Table 1. ¹H NMR chemical shifts for 3′-MOE-A₃^2′,5′ (1), 3′-MOE-A₄^2′,5′ (2), 2′-MOE-A₃^3′,5′ (3) and 2′-MOE-A₄^3′,5′ (4) at two limiting temperatures^a.

Compound	Residue	T(K)	H8	H2	H1′	H2′	H3′	H4′b	H5′b	H5′′b
1	A1	273	8.020	7.682	5.999	5.169	4.355	4.227	3.736	3.593
		343	8.110	7.937	6.084	5.162	4.313	4.260	3.786	3.658
	A2	273	7.971	7.776	5.949	4.961	4.463	4.193	4.057	3.912
		343	8.067	8.026	6.010	5.073	4.315	4.145	3.951	3.798
	A3	273	7.908	8.105	5.836	4.474	4.158	4.298	4.161	4.056
		343	8.093	8.235	5.905	4.522	4.096	4.226	4.047	4.003
2	A1	273	8.031	7.691	6.019	5.211	4.391	4.219	3.718	3.587
		343	8.086	7.937	6.078	5.162	4.313	4.251	3.781	3.655
	A2	273	7.852	7.826	5.851	4.685	4.272	4.127	3.997	3.937
		343	7.984	8.008	5.945	4.927	4.220	4.081	3.905	3.798
	A3	273	7.880	7.779	5.875	5.102	4.464	4.231	4.112	4.031
		343	8.036	8.022	5.989	5.113	4.331	4.195	4.003	3.952
	A4	273	7.892	8.110	5.825	4.401	4.135	4.143	c	4.054
		343	8.077	8.228	5.895	4.500	4.081	4.098	c	3.993
3	A1	275	8.210	7.917	5.924	4.586	4.760	4.384	3.867	3.828
		323	8.228	8.127	5.954	4.587	4.789	4.376	3.812	3.783
	A2	275	8.237	8.082	5.946	4.472	4.830	4.536	4.256	4.198
		323	8.343	8.182	6.036	4.601	4.889	4.534	4.188	4.188
	A3	275	8.253	7.979	6.046	4.351	4.550	4.359	4.279	4.192
		323	8.375	8.145	6.119	4.505	4.532	4.378	4.243	4.203
4	A1	275	8.201	7.902	5.913	4.583	4.736	4.385	3.864	3.828
		323	8.223	8.124	5.947	4.583	4.784	4.373	3.799	3.799
	A2	275	8.178	7.856	5.850	4.338	4.746	4.511	4.294	4.232
		323	8.303	8.077	5.970	4.562	4.860	4.529	4.219	4.219
	A3	275	8.122	7.879	5.866	4.508	4.806	4.537	4.244	4.192
		323	8.313	8.082	6.013	4.529	4.861	4.519	4.175	4.175
	A4	275	8.204	8.108	6.030	4.284	4.533	4.385	4.275	4.167
		323	8.372	8.197	6.115	4.520	4.594	4.381	4.240	4.202

^aChemical shifts are in p.p.m. (±0.001 p.p.m.).

^bChemical shifts for H4′, H5′ and H5′′ resonances in 1–4 have been extracted from DQF-COSY spectra and are for 1 and 2 reported at 275 and 323 K. All other chemical shifts for 1 and 2 are reported at 273 and 343 K.

^cH5′ resonance in residue A4 in 2 could not be extracted due to the overlap with CH₂ protons.

Table 2. J_HH, J_HP and J_CP coupling constants in 3′-MOE-A₃^2′,5′ (1), 3′-MOE-A₄^2′,5′ (2) and 2′-MOE-A₃^3′,5′ (3) at 275 and 323 K^a.

			JHH					JHP			JCP
	Residue	T	1′2′	2′3′	3′4′	4′5′	4′5′′	2′P	5′P	5′′P	1′P2′	3′P2′	4′P5′
1	A1	275	3.4	4.7	5.6	3.5	3.9	8.9	-	-	3.7	3.3	-
		323	4.6	5.0	4.7	4.2	4.3	9.0	-	-	5.9	3.3	-
	A2	275	3.0	5.1	6.5	3.8	4.1	9.8	2.4	2.1	6.6	2.3	9.2
		323	3.8	5.2	5.9	4.4	4.1	9.4	3.6	2.8	5.9	3.0	9.6
	A3	275	4.5	4.8	4.9	b	3.7	-	b	2.6	-	-	9.2
		323	4.7	5.2	4.6	3.8c	3.7c	-	b	b	-	-	9.2
2	A1	275	3.5	4.8	5.6	3.4	3.7	9.2	-	-	4.4	4.4	-
		323	4.7	5.1	4.8	4.1	4.0	9.0	-	-	5.9	4.1	-
	A2	275	2.0	4.4	b	3.4	4.6	9.3	4.9	2.6	3.8	4.4	7.6
		323	3.1	5.0	b	3.8	4.3	8.9	3.0	1.4	4.4	4.4	7.9
	A3	275	3.2	5.2	5.9	4.6	4.4	9.5	1.6	5.2	3.5	6.4	7.9
		323	3.9	5.3	5.5	3.8	4.6	9.3	b	b	5.6	3.5	9.1
	A4	275	4.0	4.7	5.5	b	3.6	-	b	3.3	-	-	10.6
		323	4.6	5.0	5.0	3.8	3.8	-	b	b	-	-	9.1
	Residue	T	1′2′	2′3′	3′4′	4′5′	4′5′′	3′P	5′P	5′′P	2′P3′	4′P3′	4′P5′
3	A1	275	4.8	4.5	4.6	4.6	4.9	8.3	-	-	3.6	2.2	-
		323	6.0	4.9	3.4	b	b	8.1	-	-	5.3	3.3	-
	A2	275	4.3	4.5	5.4	5.1	5.1	8.5	3.2	3.4	2.8	4.3	6.8
		323	5.7	4.9	4.0	b	b	8.0	b	b	5.8	3.7	8.7
	A3	275	4.5	4.9	5.4	5.1	5.1	-	5.8	5.0	-	-	9.1
		323	5.4	5.4	4.4	3.4c	3.9c	-	3.9	4.9	-	-	8.9

^aHomo- and hetero-nuclear coupling constants are given in Hz (±0.1 Hz for J_HH, ±0.2 Hz for J_HP and ±0.4 Hz for J_CP). Temperature is in K.

^bOverlap in the spectrum prevented the extraction of the individual coupling constants.

^cCoupling constants at 298 K are given because signals for H5′ and H5′′ protons were isochronous at 323K.

¹H NMR chemical shifts and base–base stacking interactions

The analysis of base–base stacking interactions with the use of chemical shifts is usually based on the curvature observed in the plots of chemical shifts as a function of temperature. The perusal of proton chemical shift changes as a function of increasing temperature in oligonucleotides 3′-MOE-A₃^2′,5′ (1), 3′-MOE-A₄^2′,5′ (2), 2′-MOE-A₃^3′,5′ (3) and 2′-MOE-A₄^3′,5′ (4) showed that H8, H2 and sugar H1′, H2′ and H3′ protons exhibited almost linear dependence between 273 and 343 K. The lack of significant curvature in the plots of chemical shifts (δ) as a function of temperature, in particular in 1 and 2, prevented their analysis in terms of a two-state stack ↔ unstack equilibrium (26). The chemical shift changes of aromatic and sugar proton resonances in the temperature range from 273 to 343 K (Δδ_tot) were below 0.1 p.p.m. except for H2 protons which showed Δδ_tot values of up to 0.284 p.p.m. (Table 1). In comparison, ApApA exhibited the overall changes of chemical shifts up to 0.380 p.p.m. in the temperature range from 277 to 348 K (27). H2 protons in 3′,5′-linked adenine oligonucleotides were shown to offer the best indication of stacking interactions without significant interference of factors other than the ring current effects (27,28). The chemical shifts of H8 and H2 in 3′,5′-linked 3 and 4 (except H8 in 5′-terminal residues) showed a slight curvature, but an overall change of the chemical shift in 273–343 K temperature range was comparable with Δδ_tot values in 2′,5′-linked 1 and 2 (Table 1). An additional set of measurements for 2′-MOE-A₃^3′,5′ (3), at 10 times lower concentration of 1.3 mM, also showed a slight curvature in chemical shift changes with slightly smaller Δδ_tot values of up to 0.224 p.p.m. We therefore concluded that the stacking in 1–4 is weak. The small ¹H NMR chemical shift changes in all studied oligonucleotides 1–4 reflect continuous (intra)molecular destacking over the temperature range of 273–343 K. It is noteworthy that the stacking interactions are comparable in 2′,5′-linked 1 and 2 and in their 3′,5′-linked analogs 3 and 4. Previous comparisons of the stacking properties in 2′,5′- versus 3′,5′-linked oligonucleotides (29–31) showed stronger stacking interactions in the former.

In 1981 Altona and coworkers described a correlation between the extent of stacking and the conformational preference for γ⁺ rotamers across C4′-C5′ bonds (29). The increased γ⁺ population in a given residue of an oligomer in comparison to monomeric adenosine 5′-methylmonophosphate (MepA) indicates higher population of stacked states (29). In 2′,5′-linked oligonucleotides, 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2), the preference for γ⁺ rotamers at 275 K is from 45 to 64% in all residues (see below and Table 4), which is considerably below the 85% found for MepA at 275 K (29) and clearly shows, if any, a minor fraction of conformers with stacked residues. At higher temperatures the population of γ⁺ rotamers in 1 and 2 is reduced, which is indicative of destacking. The limitation of such interpretation lies in the assumption that γ torsion angles in individual rotamers in 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2) are equal to those in MepA and thus contribute to the difference in the limiting coupling constants and therefore γ populations. The population of γ⁺ rotamers in 2′-MOE-A₃^3′,5′ (3) is <39% at 275 K (Table 4) and therefore suggests very weak intramolecular stacking interactions. It is noteworthy that higher γ⁺ populations in 2′,5′-linked oligonucleotide 1 in comparison to 3′,5′-linked 3 are in agreement with the previous results of stronger tendency to stack in 2′,5′- in comparison to 3′,5′-linked dimers and linear trimers (29) or in branched oligomeric RNAs (30).

Table 4. Conformational preferences across β, γ and ε torsion angles in 3′-MOE-A₃^2′,5′ (1), 3′-MOE-A₄^2′,5′ (2) and 2′-MOE-A₃^3′,5′ (3) at two limiting temperatures^a.

			β	γ			ε
Compound	Residue	T	%βt	%γ+	%γt	%γ–	εt	ε–	%εt	r.m.s.	ΔJmax
1	A1	275	-	60	23	17	232	275	61	0.065	0.1
		323	-	49	26	25			56
	A2	275	83	55	25	20	243	279	89	0.496	0.8
		323	86	50	23	27			74
	A3	275	83	-	-	-	-	-	-	-	-
		323	83	60 b	20 b	20 b
2	A1	275	-	64	21	15	221	262	53	0.142	0.2
		323	-	53	23	24			26
	A2	275	67	54	31	15	227	265	67	0.514	0.6
		323	70	53	27	20			55
	A3	275	70	45	26	29	218	256	70	0.405	0.6
		323	81	50	30	20			28
	A4	275	96	-	-	-	-	-	-	-	-
		323	81	59	21	20
3	A1	275	-	39	32	29	246	345	76	0.131	0.3
		323	-	-	-	-			62
	A2	275	59	32	33	35	233	295	79	0.136	0.2
		323	78	-	-	-			66
	A3	275	82	32	33	35	-	-	-	-	-
		323	79	61b	23b	16b

^aThe population of rotamers across β, γ, and ε torsion angles are in %, the values of ε^t and ε^– torsions are in degrees, r.m.s. and ΔJ^max are in Hz.

^bPopulations of γ rotamers are given at 298 K.

N ↔ S pseudorotational equilibrium

The conformational equilibria of sugar moieties in oligonucleotides 1–4 were assessed with the use of temperature-dependent ³J_1′2′, ³J_2′3′ and ³J_3′4′ proton–proton coupling constants (for data at two limiting temperatures see Table 2). The experimental ³J_HH coupling constants, which were acquired at 11 different temperatures between 273 and 343 K, were interpreted in terms of a two-state N ↔ S pseudorotational equilibrium (12,32,33). The best fit between the experimental and calculated ³J_HH was found through iterative optimization of phase angle of pseudorotation and maximum puckering amplitudes of N (P_N and Ψ_m^N) and S (P_S and Ψ_m^S) pseudorotamers as well as their respective mole fractions. Pseudorotational analysis showed that N-type pseudorotamers of individual residues in 1–4 (Table 3) exhibit puckering with the phase angles (P_N) in the range from –9 to 32° (i.e. between C3′-endo/C2′-exo and C3′-endo canonical forms). Their partners in the south region of conformational space showed P_S from 131 to 161° (between C2′-endo/C1′-exo and C2′-endo canonical forms, Table 3). The puckering amplitudes (Ψ_m) of both N and S pseudorotamers were found between 34 and 37°. The sugar moieties of A1 and A2 residues in 3′-MOE-A₃^2′,5′ (1) exhibit preference of 68 and 72% for N-type pseudorotamers at 273 K, respectively (Table 3). The population of the major N-type conformers is decreased from 68 to 49% in residue A1 and from 72 to 58% in residue A2 upon increase of temperature from 273 to 343 K (Fig. 1A). On the other hand, the residue A3 in 3′-MOE-A₃^2′,5′ (1) showed almost unbiased pseudorotational conformational equilibrium in the entire temperature range (Fig. 1A).

Table 3. N ↔ S pseudorotational equilibrium^a in 1–4.

Compound	Residue	PN	ΨmN	PS	ΨmS	r.m.s. error	ΔJmax	%N (273 K)	%N (343 K)
3′-MOE-A32′,5′ (1)	A1	–7	36	147	36	0.07	0.1	68	49
	A2	14	34	144	34	0.06	0.1	72	58
	A3	12	34	158	34	0.10	0.2	52	49
3′-MOE-A42′,5′ (2)	A1	–9	36	143	36	0.06	0.1	67	49
	A2	0	36	145	36	0.14	0.3	86	66
	A3	–8	35	131	35	0.07	0.1	69	57
	A4	11	35	154	35	0.08	0.2	60	50
2′-MOE-A33′,5′ (3)	A1	–1	36	158	36	0.09	0.3	50	33
	A2	2	37	151	37	0.10	0.3	58	36
	A3	32	34	161	34	0.13	0.3	59	43
2′-MOE-A43′,5′ (4)b	A1	–1	36	158	36	-	-	55	34
	A2	2	37	151	37	-	-	60	37
	A3	2	37	151	37	-	-	60	38
	A4	32	34	161	34	-	-	61	44

^aPhase angles of pseudorotation (P_N and P_S) and maximum puckering amplitudes (Ψ_m^N and Ψ_m^S) are in degrees, temperature is in K, r.m.s. error and ΔJ^max are in Hz.

^bPseudorotational equilibrium of 4 was evaluated only on the basis of temperature-dependent ³J_1′2′ coupling constant with the assumption of North and South conformers as they were found in 3.

Figure 1.

The populations of North conformers as a function of temperature in individual residues in (A) 3′-MOE-A₃^2′,5′ (1), (B) 3′-MOE-A₄^2′,5′ (2), (C) 2′-MOE-A₃^3′,5′ (3) and (D) 2′-MOE-A₄^3′,5′ (4). Straight lines are the best fits through experimental data points. Labels on the straight lines indicate residue numbers.

All four residues in 3′-MOE-A₄^2′,5′ (2) show a preference of >60% for N-type sugar conformation at 273 K (Table 3). The populations of N-type conformers decrease from 67 to 49% for A1, from 86 to 66% for A2, from 69 to 57% for A3 and from 60 to 50% for A4 in 3′-MOE-A₄^2′,5′ (2) with the increase in temperature from 273 to 343 K (Fig. 1B).

3′,5′-linked analogs, 2′-MOE-A₃^3′,5′ (3) and 2′-MOE-A₄^3′,5′ (4) show a conformationaly unbiased N ↔ S equilibrium at 273 K in comparison to 2′,5′-linked oligomers 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2) (Table 3). The populations of N-type conformers in 2′-MOE-A₃^3′,5′ (3) decrease from 50 to 33% in A1, from 58 to 36% in A2 and from 59 to 43% in A3 with the increase in temperature from 273 to 343 K (Fig. 1C). A comparable decrease in the populations of N-type conformers from 55 to 34% in A1, from 60 to 37% in A2, from 60 to 38% in A3 and from 61 to 44% in A4 has been observed in tetramer 2′-MOE-A₃^3′,5′ (4) with the increase in temperature from 273 to 343 K (Fig. 1D).

The van’t Hoff analysis using populations of the N and S pseudorotamers at 11 different temperatures enabled us to calculate the enthalpy and entropy contributions to the drive of the N ↔ S equilibrium for the individual residues in 1–4 (Fig. 2). The bar plots in Figure 2 show that the pseudorotational equilibrium is driven towards major N-type conformers by enthalpy contributions. Entropy terms drive the N ↔ S equilibrium in 1–4 towards S. The conformational purity in 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2) is reduced at higher temperatures due to the increased entropy contribution, which becomes equal to enthalpy.

Figure 2.

The experimental thermodynamic parameters for N ↔ S equilibrium [ΔH⁰ (dashed bars), –TΔS⁰ at 298 K (gray bars), ΔG⁰ (white bars)] in various adenosine trimers. Individual residues in oligonucleotides are denoted with A1–A4 beginning from the 5′-terminal end. A positive sign of ΔH⁰, –TΔS⁰ and ΔG⁰ denotes a drive of the N ↔ S pseudorotational equilibrium towards the North-type conformers, whereas the negative sign denotes the drive towards South-type conformers. The values of ΔH⁰ and ΔS⁰ were calculated from slopes and intercepts of van’t Hoff plots according to the relation: ln (X_S/X_N) = –(ΔH⁰/R)(1000/T) + ΔS⁰/R. The Pearson correlation coefficients of van’t Hoff plots were –0.995 for A1 in 1, –0.990 for A2 in 1, –0.811 for A3 in 1, –0.991 for A1 in 2, –0.993 for A2 in 2, –0.974 for A3 in 2 and –0.992 for A4 in 2. Thermodynamic quantities for ApApA and 3′d(A2′p5′A2′p5′A) were calculated from reported populations (27,40).

Conformational equilibria along the sugar–phosphate backbone

The population of rotamers across C4′-C5′ bond (torsion angle γ) has been evaluated on the basis of experimental ³J_4′5′ and ³J_4′5′′ proton–proton coupling constants (Table 2), which have been interpreted with the assumption of the conformational equilibrium between three staggered conformers (34). The results shown in Table 4 indicate that γ⁺ rotamers predominate in all residues in 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2). The populations of the major γ⁺ rotamers vary from 45 to 64% at 275 K and decrease with an increase in temperature (Table 4). The analysis of populations across C4′–C5′ bonds in 3′,5′-linked oligonucleotides 2′-MOE-A₃^3′,5′ (3) and 2′-MOE-A₄^3′,5′ (4) was hampered due the strong overlap of sugar resonances that prevented the analysis in 2′-MOE-A₄^3′,5′ (4) in particular and made it only partly possible in trimer 2′-MOE-A₃^3′,5′ (3). The populations of γ⁺, γ^– and γ^t rotamers were comparable in 2′-MOE-A₃^3′,5′ (3) (Table 4), except in A3 residue, where γ⁺ rotamers were predominant at higher temperatures (61% at 298 K).

The conformational equilibria across C5′–O5′ bonds (torsion angle β) were assessed with the use of the experimental ³J_C4′P coupling constants (Table 2) (35). β^t conformers were populated by >59% in the temperature range of 275–323 K in 1–3 (Table 4). Small changes in ³J_C4′P coupling constants, which were determined from 2D ¹H-¹³C HSQC (digital resolution of ±0.4 Hz) spectra, did not allow us to evaluate minor conformational redistribution across β torsion angle as a function of temperature and make correlations with the other degrees of freedom (Table 4).

The conformational analysis across C2′–O2′ bond (torsion angle ε′, for simplicity named just ε) in 1 and 2, with the use of experimental ³J_C3′P, ³J_C1′P and ³J_H2′P coupling constants, has been performed with the assumption of a two-state ε^t ↔ ε^– conformational equilibrium. A similar assumption is usually made in 3′,5′-linked analogs (14,36). This assumption was supported by our MD simulation on 3′-MOE-A₃^2′,5′ (1), which showed the equilibrium between only two conformers, one in trans region with ε ∼195° and the other in gauche^– region with ε ∼285°. Conformational analysis of coupling constants has shown that ε^t rotamers in 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2) occupy angles from 218 to 243°, while the characteristic torsion angles for ε^– rotamer are between 256 and 279° (Table 4). ε^t conformers are slightly preferred in 1 and 2 by 53–89% at 275 K. The two-state ε^t ↔ ε^– conformational equilibrium shifts towards ε^– conformers in 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2) upon the increase in temperature. The precision of ³J_CP coupling constants (± 0.4 Hz) at three temperatures (275, 298 and 323 K) hampered our interpretations with the three-parameter Karplus type equations. Additionally, parameters of the Karplus equation that have been derived empirically from data on nucleotides with 3′,5′-linked sugar–phosphate backbone (36–38) are probably different for 2′,5′-linked backbone. Nevertheless, the increase of ε^– rotamer population in 1 and 2 is correlated with the increase in the population of S-type conformers. This is in agreement with earlier studies on monomeric 3′-ethylphosphate nucleotides, which have shown that N ↔ S pseudorotational equilibrium and ε^t ↔ ε^– equilibrium are strongly coupled and exhibit (N, ε^t) ↔ (S, ε^–) equilibrium (14).

Conformational equilibria along glycosidic torsion angles in 1 and 2

The populations of syn- and anti-rotamers around torsion angle χ[O4′-C1′-N9-C4] have been assessed semi- quantitatively by the comparison of intraresidual H1′-H8 versus H2′-H8 and H3′-H8 NOESY cross-peak volumes. The anti orientation of adenine is slightly preferred in the case of A1 residues (i.e. 5′-end) in both 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2) at 275 K. The spectral overlap prevented the integration of H2′ and H3′ crosspeaks in all other residues in both 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2). H8-H1′ cross-peaks were, however, well resolved and their volumes were larger than those for A1 in 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2), which suggests that A2, A3 and A4 residues adopt predominantly syn conformation.

Orientation of MOE group in 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2)

Heavy signal overlap of 3′-MOE protons in 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2) prevented the assignment and extraction of ³J_HH coupling constants, which could define the relative orientation of 3′-OCH₂CH₂O fragments. In addition, the methyl groups of 3′-MOE in 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2) did not give any NOE cross-peaks with aromatic and sugar resonances, which is in agreement with very fast conformational changes (short correlation time) and implies weak NOE interactions. The 3′-O-CH₂CH₂-O- fragment is, however, expected to preferentially adopt gauche orientation of vicinal oxygen atoms (39). Our MD calculations on 3′-MOE-A₃^2′,5′ (1) showed comparable preferences of ∼30% for gauche⁺, gauche^– and trans populations for O-C-C-O torsion angles in MOE groups.

DISCUSSION

How do 2′-phosphate and 3′-MOE groups drive pseudorotational equilibria in 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2)?

Thermodynamics of a two-state N ↔ S pseudorotational equilibrium in nucleosides and nucleotides were recently rationalized on the basis of competing steric, gauche and anomeric effects that were evaluated in a quantitative manner (12,15,16). It is noteworthy that the drive of the N ↔ S equilibrium by stereoelectronic forces was evaluated in the absence of any intramolecular stacking interactions due to the intrinsic structural features of mononucleosides and nucleotides. The N ↔ S equilibrium in individual residues of 2′,5′-linked oligonucleotides 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2) is driven towards N by the anomeric effect of adenine and by the gauche effect of the [O4′-C1′-C2′-O2′] fragment (Fig. 3A), and towards S by the gauche effects of [O4′-C4′-C3′-O3′] fragment and [N9/1-C1′-C2′-O2′] fragments (Fig. 3B). The steric effects drive N ↔ S equilibrium through the preference of bulky substituents to adopt pseudoequatorial orientation (e.g. adenine would adopt S-type conformation due to the steric effect alone, while 3′-MOE group would prefer N-type sugar conformation in 1 and 2, Fig. 3).

Figure 3.

Relative orientations of adenine, phosphodiester functionality, 3′-MOE group and other substituents in (A) N- and (B) S-type conformers of non-terminal residues in 2′,5′-linked oligonucleotides 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2). The 3′-MOE group adopts pseudoequatorial orientation in the N-type conformation (A). In addition, oxygen atoms of 3′-MOE group which adopt gauche orientation are predisposed for water-mediated H-bonding interactions with 2′-phosphodiester functionality. In S-type conformation the 3′-MOE group adopts less favorable pseudoaxial orientation (B).

It has been shown that the gauche effects of [O4′-C4′-C3′-O3′PO₃H^–] and [O4′-C4′-C3′-O3′PO₃Et^–] fragments are stronger by 1.2 and 0.8 kJ mol^–1, respectively, than the gauche effect of the [O4′-C4′-C3′-O3′H] fragment in 2′-deoxyadenosine (13). Similarly the gauche effect of 3′-ethylphosphate is stronger by 2.3 kJ mol^–1 than the gauche effect of 3′-OH in adenosine (14). In 2′,5′-linked oligonucleotides 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2) the phosphate group is at the 2′-position and thus stabilizes N-type conformers by the gauche effect of [O4′-C1′-C2′-O2′PO₂OR^–] fragments (Fig. 3A). The preferential stabilization of N-type conformers by 2′-phosphate over 2′-hydroxy functionality is nicely manifested by the additional stabilization of N-type conformation by up to 26 unit % for non-2′-terminal residues in 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2) (Table 3). The drive towards N-type conformers is perhaps best appreciated through the comparison of thermodynamic parameters depicted in Figure 2. The enthalpy that drives the N ↔ S pseudorotational equilibria towards N-type conformers is opposed by the entropy term of similar strength at 298 K.

To further evaluate the impact of gauche effects in 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2) we have made comparisons of their conformational properties with those in trimeric adenine oligonucleotides with different substituents at atom C3′. N ↔ S equilibria in non-2′-terminal residues of 3′d(A2′p5′A2′p5′A) are conformationaly strongly biased towards N by ∼94% at 298 K (40) (Table 5). The high conformational purity of sugar moieties in 3′d(A2′p5′A2′p5′A) can be attributed to the gauche effect of the [O4′-C1′-C2′-O2′PO₂OR^–] fragment and anomeric effect of adenine, which both drive N ↔ S equilibrium towards N. There is no opposing gauche effect of 3′-O substituent, which would drive N ↔ S equilibrium towards S. In comparison, the pseudorotational equilibria in A2′p5′A2′p5′A, where H3′ is substituted with 3′-OH group (29), showed only slight preference for N-type conformers (Table 5). The examination of thermodynamic contributions to the drive of N ↔ S equilibrium nicely illustrates the effect of 3′-H, 3′-OH and 3′-MOE modifications on the sugar conformation in 2′,5′-linked trimers (Fig. 2A). The drop in ΔH° values in 3′-OH and 3′-MOE analogs, in comparison to the parent 3′-deoxy trimer 3′d(A2′p5′A2′p5′A), which is correlated with the reduced stabilization of N-type pseudorotamers, can be explained by the gauche effect of the [O4′-C4′-C3′-O3′] fragment that drives N ↔ S equilibrium towards S-type conformers. It is noteworthy that the gauche effect of the [O4′-C4′-C3′-O3′] fragment is apparently stronger in A2′p5′A2′p5′A in comparison to 3′-MOE-A₃^2′,5′ (1) (Fig. 2 and see below).

Table 5. Comparison of conformational parameters in various 2′,5′- and 3′,5′-linked adenosine trimers^a at 298 K.

Compound	Residue	PN	ΨmN	PS	ΨmS	%N
3′-MOE-A32′,5′ (1)	A1	–7	36	147	36	58
	A2	14	34	144	34	68
	A3	12	34	158	34	52
3′d(A2′p5′A2′p5′A)b	A1	15	31	162	34	93
	A2	11	32	162	34	94
	A3	11	31	161	34	78
A2′p5′A2′p5′Ab	A1	14	33	160	33	55
	A2	3	33	148	33	61
	A3	16	33	159	33	55
2′-MOE-A33′,5′ (3)	A1	–1	36	158	36	41
	A2	2	37	151	37	47
	A3	32	34	161	34	47
2′d(ApApA)b	A1	10	35	168	35	8
	A2	10	35	152	36	10
	A3	10	35	144	32	34
ApApAb	A1	-	-	-	-	66
	A2	-	-	-	-	72
	A3	-	-	-	-	63

^aPhase angles of pseudorotation (P_N and P_S) and puckering amplitudes (Ψ_m^N and Ψ_m^S) are in degrees, temperature is in K and populations of N-type conformers at 298 K are in %.

^bN ↔ S equilibria for dApdApdA (26), A2′p5′A2′p5′A (29) and 3′d(A2′p5′A2′p5′A) (40) were reassessed with the PSEUROT program with the use of ³J_HH coupling constants reported previously. Populations of N-type conformers in ApApA are taken from the original paper (27).

Effect of MOE group on the N ↔ S equilibrium in 2′,5′-linked and 3′,5′-linked oligomers

The pairwise comparison of N ↔ S equilibria of A1 and A2 residues in 2′,5′-linked 3′-MOE-A₃^2′,5′ (1) and in A2′p5′A2′p5′A at 298 K shows that N-type conformers are preferred by 3 and 7 unit % in the former, respectively (Table 5). N-type conformers of A1 and A2 are preferentially stabilized in 3′-MOE-A₃^2′,5′ (1) in comparison to A2′p5′A2′p5′A by ΔΔH⁰ of 3.1 and 4.2 kJ mol^–1, respectively (Fig. 2). The strength of the gauche effect of [O4′-C4′-C3′-O3′] fragment, which drives N ↔ S pseudorotational equilibrium towards S is apparently decreased in 3′-MOE-A₃^2′,5′ (1). The weaker gauche effect of the [O4′-C4′-C3′-O3′] fragment could be due to the smaller electron withdrawing nature of MOE group in comparison to OH group. An additional reason for the 3′-MOE group to stabilize N-type conformers, in comparison with the 3′-OH group in 2′,5′-linked oligonucleotides, lies in the possibility of water-mediated H-bond formation between the 3′-MOE group and 2′-phosphate oxygen atoms (4). It is reasonable to assume that the ethylenic fragment of the MOE group in all studied oligomers 1–4 adopts a gauche orientation (39). Such orientation is predisposed for water-mediated H-bonding interactions of -OCH₂CH₂O- fragment with vicinal phosphodiester functionality at 2′ position in 1 and 2 (Fig. 3A). The structural and spatial requirements for water-mediated H-bonding interactions between phosphate oxygens and 3′-O-CH₂CH₂-O- oxygens were analyzed on a series of structures obtained from our in vacuo MD simulations of 3′-MOE-A₃^2′,5′ (1). In the final 1 ns of our 3 ns MD simulation A2 residues showed distances between phosphate oxygens and 3′-O-CH₂CH₂-O- oxygens from 3 to 5 Å, which supports the possibility of water-mediated H-bond formation.

The other possible explanation for the stabilization of N-type conformers in 1 and 2 involves the steric interactions of the 3′-MOE group, which plays an important role in the drive of N ↔ S equilibrium in 3′-MOE-substituted 2′,5′-linked oligonucleotides. It has been shown (12,15,16,41) that bulky substituents in mononucleos(t)ides (e.g. nucleobase) adopt pseudoequatorial orientation (Fig. 3B). In the case of 2′,5′-linked 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2), the MOE group at C3′ adopts pseudoequatorial position in N-type conformation. The gauche effect of the [O4′-C4′-C3′-O3′] fragment is therefore opposed by the steric effect of the 3′-MOE group. This fine tuning of N ↔ S equilibrium in 1 and 2 is in perfect agreement with experimentally determined conformational preferences (Table 5).

The comparison of N ↔ S conformational preferences in both 2′,5′- and 3′,5′-linked oligonucleotides gives additional insight into the effects and roles that 3′-MOE as well as 2′-MOE groups play in the drive of pseudorotational equilibria of sugar rings in 1–4. N ↔ S equilibria of A1 and A2 in dApdApdA with the 3′,5′-linked backbone (26) show high conformational bias towards S-type conformers at 298 K (Table 5). The high conformational purity can be attributed to the gauche effect of the [O4′-C4′-C3′-O3′] fragment, which stabilizes S type conformers. The lower population of S-type conformers in the 3′-terminal residue of dApdApdA can be explained by the weaker gauche effect of [O4′-C4′-C3′-O3′H] and therefore the weaker drive towards S in comparison to the [O4′-C4′-C3′-3′phosphate] fragment.

The replacement of H2′′ in dApdApdA with 2′-OH group in ApApA shifts the N ↔ S equilibrium strongly towards N with the populations from 63 to 72% at 298 K (Table 5). The shift towards N-type conformers by 58 and 62 unit % for A1 and A2 in ApApA in comparison to dApdApdA can be rationalized by the gauche effect of the [O4′-C1′-C2′-O2′] fragment which drives N ↔ S equilibrium towards N and therefore opposes the gauche effect of the [O4′-C4′-C3′-O3′] fragment. The 2′-OH group of sugar moieties in ApApA is, in addition, involved in the gauche effect of the [N9-C1′-C2′-O2′] fragment, which drives N ↔ S equilibrium towards S, but is apparently weaker. Shift towards N-type conformers can also be promoted by the involvement of the 2′-OH group in H-bonds with vicinal 3′-phosphate oxygens (42).

The comparison of conformational preferences and thermodynamic data for the N ↔ S equilibrium in ApApA and 2′-MOE-A₃^3′,5′ (3) shows that the 2′-MOE group apparently shifts the N ↔ S equilibrium towards S-type conformers by 25 unit % in 3′-non-terminal residues (Table 5). The substitution of 2′-OH group with 2′-MOE affects the strength of two gauche effects that oppose each other in the drive of pseudorotational equilibrium. The gauche effect of the [O4′-C1′-C2′-O2′] fragment drives N ↔ S pseudorotational equilibrium towards N, while the gauche effect of [N9-C1′-C2′-O2′] fragment drives it towards S conformers. The large shift towards S-type conformers in 2′-MOE-A₃^3′,5′ (3) cannot be explained solely by the gauche effects of the 2′-MOE group. The 2′-MOE group in 3′,5′-linked oligonucleotides adopts sterically less hindered pseudoequatorial orientation in the S-type conformation. S-type conformation is also preferred by the steric effect of the adenine base where it can interact with the vicinal 2′-MOE group. Such stabilization by interactions of the MOE group and adenine could not occur in 2′,5′-linked analogs where the MOE group is at the 3′ position. Pyrimidine nucleosides and nucleotides are, in comparison with their purine counterparts, characterized by a higher conformational bias towards N-type conformations due to the stronger anomeric effects of cytosine and thymine (12). In 2′,5′-linked pyrimidine oligomers the anomeric effect and gauche effect of the 2′-phosphodiester would therefore both drive the N ↔ S equilibrium towards N-type conformers, which would be opposed by the gauche effect of the 3′ substituent. It can be predicted that pyrimidine trimers and tetramers would therefore exhibit higher preferences for the N-type sugar conformation.

In conclusion, trinucleoside diphosphates 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2) were prepared as novel modifications of antisense oligonucleotides with unique 2′,5′-phosphodiester linkages and 3′-MOE functionalities. The study of conformational properties of 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2) by NMR spectroscopy revealed A-type conformational features that are prerequisite for good antisense hybridization. The interpretation of temperature-dependent ³J_HH coupling constants in terms of a two-state N ↔ S pseudorotational equilibrium gave insight into the thermodynamics of the drive towards N-type conformers by 2′-phosphate groups in 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2). 3′-MOE groups in 3′-MOE-A₃^2′,5′ (1) and 3′-MOE-A₄^2′,5′ (2) drive N ↔ S pseudorotational equilibrium additionally towards N-type conformers in comparison to 3′-OH in the analogous trimer and tetramer oligonucleotide. Conformational equilibria around the sugar–phosphate backbone showed a predominance of β^t, γ⁺ and ε^t rotamers.