Mechanism of the single-headed processivity: Diffusional anchoring between the K-loop of kinesin and the C terminus of tubulin

Abstract

A motor-domain construct of KIF1A, a single-headed kinesin superfamily protein, was demonstrated to take more than 600 steps before detaching from a microtubule. However, its molecular mechanism remained unclear. Here we demonstrate the nucleotide-dependent binding between the lysine-rich, highly positively charged loop 12 of the KIF1A motor domain (K-loop) and the glutamate-rich, highly negatively charged C-terminal region of tubulin (E-hook). This binding did not contribute in the strong binding state but only in the weak binding state. This binding was demonstrated to be essential for the single-headed processivity by functioning as the anchor for the one-dimensional simple Brownian movement in the weak binding state. This Brownian movement will allow the small KIF1A motor domain to span the distance between the binding sites on microtubule and also will give the diffusive nature to the movement of single KIF1A molecules. These observations quantitatively fitted well to the predictions made from our Brownian motor model on the mechanism of the single-headed processive movement.

A single kinesin molecule has two heads (1, 2) or motor domains and moves processively (3–5), taking more than 100 steps before detaching from a microtubule (MT). The two-headed structure is assumed to be essential for processive movement (5–8). However, we recently have demonstrated that a single-headed motor domain construct (C351) of KIF1A, a naturally monomeric kinesin superfamily protein (9), is a highly processive motor; C351 took more than 600 steps per MT encounter, making it five times more processive than the dimeric construct of conventional kinesin (10). The movement of the single C351 molecules was very stochastic; it was a kind of a biased Brownian movement.

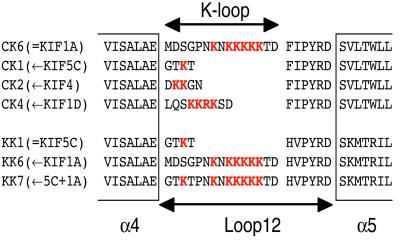
In the same paper (10), we have proposed that loop 12 or the K-loop, a putative MT-binding loop of C351 that contains six extra lysines in tandem (Fig. 1) might play an important role in keeping the motor in contact with MT for a longer time. This loop and the following His-Ile-Pro-Tyr-Arg-Asp consensus motif are considered to be involved in the kinesin-MT interaction in previous studies (10–12), but the exact function of the K-loop remained unclear.

Figure 1.

Design of the K-loop mutants. Sequences of the K-loop regions are indicated with positively charged residues in red. CK6 and KK1 are the original constructs C351 and K351 (10). For KIF1A-based mutants, the K-loop of conventional kinesin (KIF5C), KIF4 and KIF1D were used.

One possible function of the K-loop is a mobile tether. Our Brownian motor model (10), a model to explain the diffusive nature of the movement of C351, assumes that the motor is anchored to the MT in such a way that its detachment is restricted while allowing free diffusional movement along the MT. This one-dimensional (1D) diffusion will allow the small motor molecule (6 nm) to encompass the large distance (8 nm) between the binding sites along MT protofilament. Although it has not been supported by direct experimental results yet, this model could quantitatively explain the behavior of the single C351 molecules, and the K-loop is a good candidate for the mobile tether that allows the 1D diffusion.

Here, we have produced a series of conventional kinesin and KIF1A motor domain mutants with different numbers of lysines in the K-loop (Fig. 1). These mutations specifically affected the MT binding in the weak binding state (w-state), which correlated well with the processivity of the movement. Furthermore, the subtilisin digestion experiment identified the C-terminal glutamate-rich region (E-hook) of tubulin as the binding partner of the K-loop. This K-loop–E-hook interaction was essential for the 1D Brownian movement along MTs in the w-state. These results provide the direct and quantitative supports for our Brownian motor model on the processive movement of the single-headed motor.

Materials and Methods

Preparation of the K-Loop Mutants.

Expression plasmids for the K-loop mutants of C351 (KIF1A) and K351 (murine conventional kinesin KIF5C) were constructed by PCR and checked by sequencing (10). Bacterially expressed protein was purified and labeled with Alexa (Molecular Probes) as described (10).

Hydrodynamic Characterization.

Hydrodynamic characterization of the K-loop mutants and their originals was performed by the standard method (9, 13) in the same buffer for the MT-binding assay.

MT-Activated ATPase Measurement.

MT-activated ATPase activity was assayed with the EnzChek phosphate assay kit (Molecular Probes) at 27°C. The concentration of MT was determined spectroscopically (14). The concentration of the motor protein was determined by Coomassie Plus Protein Assay Reagent (Pierce) using C351 as the standard. The concentration of C351 standard was determined by the binding of ³²P-ADP (15).

MT-Binding Assay.

Equilibrium binding constant of motor protein was determined according to the standard method (15) with modifications. Fluorescently labeled motor protein was incubated with MT in the motility buffer (50 mM imidazole/5 mM Mg-acetate/1 mM EGTA/50 mM K-acetate/10 mM DTT/10 μM paclitaxel, pH 7.4) supplemented with 1 mg/ml casein and 1% Triton X-100 to reduce nonspecific binding. For the ADP.Pi state, 50 mM K-acetate was replaced with 10 mM K₂PO₄ and 30 mM K-acetate. For the nucleotide-free state, 10 mM EDTA was added to the buffer. After incubation at 27°C, the sample was filtered quickly through Nanosep 300K (Pall). The filtrate was analyzed with a spectrofluorometer FP-777Win (Jasco, Tokyo).

Subtilisin Digestion of Tubulin.

Polymerized, paclitaxel-stabilized MT was digested with subtilisin (Roche) at 37°C for 15 min, followed by the centrifugation.

Single-Motor Motility Assay.

Single-motor motility assay was performed at 27°C as described (10). Bodipy-labeled polarity-marked MTs were prepared as described (16). For the ADP-state assays, hexokinase was added to the motility buffer to remove the trace amount of contaminating ATP. In all experiments, the fluorescence intensity profile of each molecule was checked to confirm its monomericity.

Results and Discussion

Construction of K-Loop Mutants.

To examine the function of the K-loop, we have produced three KIF1A motor domain mutants that have fewer lysines in their K-loop, and two conventional kinesin mutants that have more lysines in their K-loop (Fig. 1). To examine the overall structure and the oligomerization state of these mutants, hydrodynamic characterization was performed. As reported previously (10, 13), the sedimentation constants (s_20,w) of the conventional kinesin construct KK1 and the KIF1A construct CK6 were 3.5–3.6 S either in the presence of AMP-PNP (adenosine 5′-[β, γ-imido]triphosphate) or ADP. All of the K-loop mutants had similar s_20,w values (3.5–3.6 S) in the same conditions, guaranteeing that all of these constructs are monomeric.

We next examined their ATPase activity. It was activated more than 1,000 times in the presence of MT, and the turnover rates (k_cat) of these mutants were within 100 ± 20% of those of their original constructs. This finding functionally guarantees that the overall structure of these mutants was not affected by the K-loop mutations.

Contrastingly, K_MT(ATPase)^0.5 (MT concentration for half-saturation of ATPase), a measure for the averaged affinity to MT throughout the ATPase cycle, was significantly affected by the mutations in the K-loop. K_MT(ATPase)^0.5 for CK1 and CK2 was 3–5 times larger (30–50 nM) than their original, CK6 (10 ± 2 nM), whereas CK4 showed similar values (5–20 nM). KK6 and KK7 showed about 5–10 times smaller K_MT(ATPase)^0.5 values (150–250 nM) than their original KK1 (1,400 ± 200 nM). Thus, the positively charged residues in the K-loop increased the affinity to MTs.

The K-Loop Is the W-State-Specific Binding Site.

We next measured the affinity of the K-loop mutants to MT in various nucleotide conditions. The ATPase cycle of kinesin motors consists of four steps: ATP binding to the nucleotide free kinesin, hydrolysis to produce ADP.Pi state, phosphate release to produce ADP state, and the rate-limiting ADP release step. To dissect the change in these transient states, we mimicked these four states by a standard pharmacological method. Nucleotide-free state was produced by chelating out Mg²⁺ ion with EDTA. ATP state was mimicked by the nonhydrolyzable analogue AMP-PNP. The addition of excess inorganic phosphate or ADP was used to trap the motor in ADP.Pi state and ADP state, respectively.

The results of originals (KK1 and CK6) and the mutants with their K-loop swapped (CK1 and KK6) are summarized in Fig. 2A. As already reported (17–19), conventional kinesin construct KK1 showed significantly lower affinity in ADP.Pi and ADP states (the w-state) than in AMP-PNP and EDTA states (the strong binding state, s-state). In contrast, the MT affinity of KIF1A motor domain construct CK6 showed no significant nucleotide-dependent change. Quite interestingly, KK6 showed nucleotide-insensitive binding to MTs like CK6, whereas the MT binding of CK1 was nucleotide-dependent like KK1. Although the nucleotide-dependent change of the K_d value was affected by the K-loop mutation, the K_d value in the s-states (AMP-PNP and EDTA states) did not change significantly by the mutation. This finding suggests that the positive charges in K-loop contribute only in the w-state, and that the affinity in the s-state is determined by other region(s) of kinesin motor domain.

Figure 2.

Equilibrium binding constant (K_d) of K-loop mutants. Mean and SD of at least three independent experiments are shown. (A) K_d of KK1 (green), CK6 (red), CK1 (blue), and KK6 (black) in various nucleotide conditions. Binding energy ΔG = k_BT log K_d is shown on the right axis. (B) K_d of K-loop mutants in the s- and the w-states plotted against N, the number of positively charged residues in the K-loop. Black circle, conventional kinesin mutants in ADP state; blue square, conventional kinesin mutants in AMP-PNP state; green circle, KIF1A mutants in ADP state, and red square, KIF1A mutants in AMP-PNP state. (C) ΔΔG, difference of the binding energy between the s- and the w-states plotted against N. Both conventional kinesin (blue square) and KIF1A (red circle) mutants were on the same line with a slope −0.25 k_BT. (D) K_d of CK6 to subtilisin-digested MT plotted against the concentration of subtilisin (molar ratio to tubulin). K_d^w of CK6 (red) increased according to the degree of the subtilisin digestion to the level similar to K_d^w of CK1 to intact or digested MT (green), whereas K_d^s of CK6 (blue) was not significantly affected by the subtilisin digestion. (Lower) The degree of the tubulin digestion by subtilisin. The anti-α tubulin antibody recognized an epitope upstream to the subtilisin digestion site, thus subtilisin-digested α tubulin is detected as a band with higher mobility (lower band in α). The epitope of the anti-β tubulin antibody was in the subtilisin-digested region, thus subtilisin digestion results in the loss of the band.

The results with other mutants further support this conclusion. As shown in Fig. 2B, KIF1A-based constructs CK1, CK2, CK4, and CK6 all showed similar K_d values (4–6 nM) in the s-state (K_d^s), and K_d^s for the conventional kinesin-based constructs KK7, KK6, and KK1 all were within the range of 40 to 60 nM. This demonstrates that the K-loop does not contribute much in the s-state. Meanwhile, K_d values in the w-state (K_d^w) showed an exponential change according to the number of the positively charged residues in the K-loop (N). Interestingly, the difference of the binding energy between the s- and w-states (ΔΔG = k_BT log K_d^w − k_BT logK_d^s, k_B: Boltzman constant, T: temperature) changed linearly against N for both KIF1A-based mutants and conventional kinesin-based mutants along the same line: ΔΔG = 1.6 k_BT − 0.25 k_BTN (Fig. 2C). This means that each positively charged residue in the K-loop independently contributes to the binding by 0.25 k_BT only in the w-state. That is, the K-loop is a w-state-specific MT-binding site, whose positive charges interact with the negative charges on MT only in the w-state.

Furthermore, these results have two other implications. First, without the K-loop, the difference of the binding energy between the s- and the w-states was about 1.6 k_BT both in conventional kinesin and KIF1A. This finding suggests the existence of the s-state-specific binding site (s-site), which contributes specifically in the s-state by 1.6 k_BT both in conventional kinesin and KIF1A. Second, when the number of the positive charges in the K-loop are the same, the difference of the binding energy between conventional kinesin and KIF1A was about 2.4 k_BT both in the s- and the w-states. This overall difference between conventional kinesin and KIF1A will be caused by the difference of the third nucleotide-insensitive binding site (o-site), which will determine the basal level of the binding. The exact positions of these s- and o-sites awaits future structural and mutational analyses.

C Terminus of Tubulin Is the Binding Site of K-Loop.

A good candidate for the binding partner of the K-loop is the C terminus of tubulin. It contains more than eight negatively charged residues (glutamate or aspartate) in tandem and often is poly-glutamylated posttranslationally (20). Furthermore, this region is estimated to project out from the MT surface (21). Therefore, we measured the K_d of CK6 to subtilisin-digested MT, because subtilisin cleaves off the C-terminal about 20 aa (22). As shown in Fig. 2D, K_d^w in the w-state increased according to the degree of the subtilisin digestion. However, even with fully digested MTs, K_d^s of CK6 as well as K_d^s and K_d^w of CK1 were not affected significantly by the subtilisin digestion. Furthermore, the K_d^w value of CK6 with fully digested MTs was almost the same as that of CK1 with undigested (as well as digested) MTs. This finding strongly suggests that the C-terminal negatively charged, glutamate-rich stretch of tubulin is the binding partner of the K-loop, and that other binding sites of kinesin do not interact with this C-terminal region. Hereafter, we refer to this tubulin C-terminal region as the E-hook, because it contains many glutamates (E in one-letter code).

Interestingly, the removal of the E-hook by subtilisin digestion did not affect the binding affinity attributable to the putative s- and o-sites, which means that other regions of tubulin contribute to the interaction mediated by these sites. The identification of these tubulin domains also awaits future study.

Disruption of K-Loop–E-Hook Interaction Reduces Processivity of KIF1A.

How will this K-loop–E-hook interaction contribute to the processive movement? We measured the processivity of the K-loop mutants with the single-motor motility assay (10).

On the polarity marked MTs, CK4 and CK2 showed biased Brownian movement toward the MT plus end (see Fig. 4C for traces of CK4 movement), apparently similar to their original, CK6 (10), though their duration of the movement was shorter than CK6 (Fig. 3A). Nearly half of the CK6 molecules kept moving for more than 5 s, but about half of the CK4 and CK2 molecules detached from the MT within 1 s and 0.5 s, respectively. Most of the CK1 molecules were found on the MT only for one or two frames (133 ms per frame). These data were fitted with an exponential distribution, and the mean duration of the movement (τ_mec), a quantitative measure for the processivity of the movement was calculated. Fig. 3B shows the exponential relation of the τ_mec against the number of positive charges in K-loop. As shown in Fig. 3C, the processivity of CK6 and its mutants can be quantitatively explained by the affinity to the MT in the w-state by using the thermodynamic relation (line in Fig. 3C): τ_mec ∝ 1/K_d^w (10).

Figure 4.

Highly processive movement of KK6 in the low-salt buffer. (A) Intensity profile of the moving fluorescent spots. Red rectangles show the results with KK6, and black line shows the best-fit Gaussian distribution. Blue line shows the result with dimeric construct K381 (10), which has two peaks (arrows) corresponding to singly and doubly labeled molecules. KK6 showed only one peak corresponding to the single-fluorescent molecule, indicating that KK6 moving on the MT is a monomer in this condition. (B) Distribution of the duration of the movement of KK6. Line shows the best-fit curve with the mean duration of the movement τ_mec = 1.2 s. (C and D) Typical traces of the movement of CK4 in the standard buffer (C) and KK6 in the low-salt buffer (D). Positive displacement indicates the displacement toward the MT plus end. Note the fluctuating nature of the movement and the bias toward the MT plus end. (E and F) Mean displacement (E) and MSD (F) of KK6 movement (red) plotted against time. Red lines show the best-fit curves with the mean velocity v = 120 nm/s and the diffusion coefficient D = 30,000 nm²/s. Blue lines show the best-fit curves of CK4 (v = 160 nm/s, D = 44,000 nm²/s). Dotted lines in F show the diffusion term (MSD − v²t²) to illustrate the difference in the diffusion coefficient.

Figure 3.

Processive movement of K-loop mutants observed by the single-motor motility assay. (A) Distribution of the duration of the movement. (B and C) Mean duration of the movement (τ_mec), an index for the processivity of the movement plotted against N, the number of the positively charged residues in the K-loop and against K_d^w, the MT-binding constant in the w-state. (D and E) Mean displacement (D) and MSD (E) of CK6 (red), CK4 (blue), CK2 (black), and CK1 (green) plotted against time. Positive displacement indicates the movement toward the MT plus end. Red line shows a biased Brownian movement with mean velocity 160 nm/s and diffusion coefficient 44,000 nm²/s. Note that the data points of all these mutants fit nicely to these lines, indicating that they all have the same motile parameters.

Although K-loop mutations severely affected the processivity, other motile parameters were not affected. As shown in Fig. 3D, both CK2 and CK4 moved toward the MT plus end on average, and their mean velocity was the same as their original, CK6. The mean square displacement (MSD) plot in Fig. 3E also demonstrates that the parameters of the biased Brownian movement of these mutants were not affected by the K-loop mutation, which indicates that the K-loop determines only the processivity.

If the K-loop determines the processivity, its binding partner, E-hook, also will be essential for the processivity. To examine this, we prepared Bodipy-labeled, subtilisin-digested MT, in which most of the E-hook of both α and β tubulin were removed. With this E-hook-digested MT, CK6 did not show processive movement. CK6 frequently attached to the MT, but it immediately detached within a few frames, similar to CK1 on undigested MT (data not shown), which indicates that both the K-loop and E-hook are essential for the highly processive movement of CK6.

Addition of Six Extra Lysines to the K-Loop Gives High Processivity to Monomeric Conventional Kinesin.

If the K-loop alone determines the processivity of the single-headed kinesin, addition of extra lysines to the K-loop of conventional kinesin should make an artificial, highly processive monomeric conventional kinesin mutant. However, KK6, a conventional kinesin mutant with KIF1A's K-loop (six lysines), were less processive than CK1 (Fig. 3A). Most of the KK6 molecules detached from the MT within 133 ms (one frame); their duration was even shorter than CK1. This low processivity of KK6 can be quantitatively explained by the low affinity of KK6 in the w-state. Extra lysines in the K-loop did increase the affinity in the w-state by five times compared to its original, KK1, but still the affinity of KK6 in the w-state was about half of that of CK1. As shown above, the K-loop only functions as the auxiliary binding site that supplements the basal binding, which was about 10 times weaker in conventional kinesin than KIF1A (Fig. 2A). Actually, Fig. 3C shows that the low processivity of KK6 was quantitatively explained by its K_d^w.

This finding suggests that KK6 might show highly processive movement, if the basal binding strength was increased by lowering the ionic strength of the assay buffer. Our standard buffer contains 50 mM K-acetate. When this salt was removed from the buffer, the affinity of KK6 increased about five times (about 10 nM) compared to that in the standard buffer, both in the s- and w-states. This value is similar to that of CK4, suggesting a possibility that KK6 in this buffer might be as processive as CK4.

The monomericity of KK6 in this condition was confirmed by the hydrodynamic analysis (s_20,w = 3.5 S) and the fluorescence intensity profile (Fig. 4A). In this low-salt buffer, KK6 showed highly processive movement along the MT (Fig. 4B). Its processivity (τ_mec) was about 1.2 s, similar to CK4 (1.1 s), as expected from the similar K_d^w value. Fig. 4D shows several typical traces of each KK6 molecule, showing a biased Brownian movement toward the MT plus end, similar to those of CK4 (Fig. 4C), though the mean velocity of KK6 was 120 ± 10 nm/s, about 80% of that of CK4 (and CK6) (Fig. 4D), and the diffusion coefficient of KK6 was 30,000 ± 1,000 nm²/s, about 65% of CK4 (and CK6) (Fig. 4E). Thus, the basic nature of the movement of KK6 was the same as that of CK4 (and CK6).

Even in this low-salt buffer, the original construct KK1 did not show processive movement (data not shown) as reported previously (5). KK1 molecules remained on the MT for only one or two frames (133 ms per frame). Thus, increased basal binding strength alone is not enough for the highly processive movement of KK6. These results together with the poor processivity of CK1 suggest that both high basal binding strength and the strong K-loop–E-hook auxiliary binding are essential for the single-headed processivity.

1D Diffusion of KIF1A in the W-State.

These results suggest that the key mechanism of the single-headed processivity would exist in the w-state. We, therefore, directly observed the CK6-MT interaction in the w-state with the single-motor motility assay system.

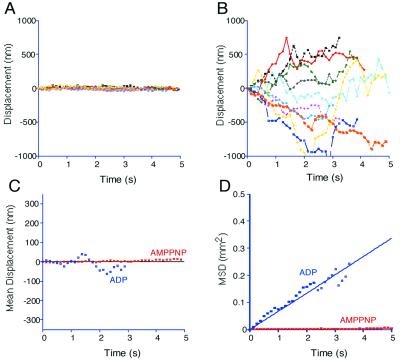
In the s-state (2 mM AMP-PNP), CK6 firmly attached to MTs. No significant displacement was observed (Fig. 5A). In the w-state (2mM ADP), however, CK6 showed 1D diffusion along the MT (Fig. 5B). The movement was directionless, not biased to either plus or minus ends of the MT (Fig. 5C). MSD plot showed a linear increase against time (Fig. 5D), clearly indicating that it is a simple Brownian movement. The diffusion coefficient of CK6(ADP) was 40,000 ± 4,000 nm²/s, almost the same value as that of the biased Brownian movement of CK6 in the presence of ATP.

Figure 5.

1D Brownian movement along the MT in the w-state. (A and B) Typical traces of CK6 movement in the presence of AMP-PNP (A) and ADP (B). Positive displacement indicates the movement toward the MT plus end. Note that the molecule did not move in the presence of AMP-PNP, but it randomly diffused back and forth in the presence of ADP. (C and D) Mean displacement (C) and MSD (D) plotted against time. Red and blue show the AMP-PNP and the ADP states, respectively. Lines show the best-fit curve. The movement of CK6 in ADP state was a simple, unbiased Brownian movement with D = 40,000 nm²/s.

With the K-loop mutant CK1 or E-hook-digested MT, rigor binding was similarly observed in the presence of AMP-PNP. However, the 1D Brownian movement was not observed in the presence of ADP (data not shown); motor molecules remained on the MT for less than a few frames. This indicates that the K-loop–E-hook interaction is essential for this 1D Brownian movement in the w-state, but not to the rigor binding in the s-state.

Mechanism of the Single-Headed Processivity.

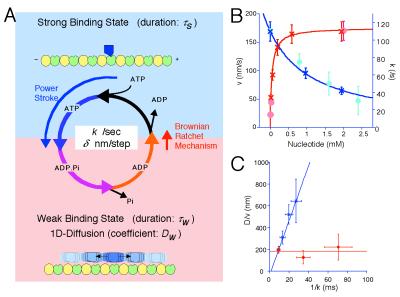
The observed 1D diffusion in the w-state is a key assumption of our Brownian motor model (10). This model was proposed to explain the single-headed processivity of KIF1A and also to explain its diffusional movement. The model is summarized in Fig. 6A. The motor cycles between the s- and w-states by the ATP hydrolysis (cycle time = 1/k, where k is the turnover rate). In the s-state (duration τ_s), the motor firmly attaches to the MT in a rigor manner, while it freely diffuses along the MT (diffusion coefficient D_w) in the w-state (duration τ_w). In each ATPase cycle, the motor moves to the MT plus end by δ on average either by the power stroke(s) during the ATP hydrolysis or by a Brownian ratchet mechanism in the w- to s-state transition (10). With this model, the mean velocity v and the apparent diffusion coefficient D are given by:

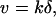1

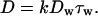2

Both the rigor binding in the s-state and the 1D diffusion in the w-state, key assumptions of this model, were directly observed by the single-motor assay. Furthermore, the observed processive movement of the K-loop mutants gives the quantitative support for this model.

Figure 6.

Brownian motor model and the ATPase perturbation experiments. (A) Summary of the Brownian motor model. Refer to text for details. (B and C) ATPase perturbation experiments. (B) Mean velocity (○) and ATPase turnover rate (×) plotted against nucleotide concentration. For the limiting ATP conditions (red), the concentration of ATP was maintained by the ATP regenerating system (23). For the ADP-addition experiment (blue), ADP was simply added to the buffer containing 2 mM ATP. (C) D/v plotted against 1/k. In the limiting ATP conditions (red), D/v was almost constant (about 190 nm). In the ADP-addition experiment (blue), D/v increase linearly against 1/k. The blue line is the theoretical prediction: D/v = 25(1/k − 1.5).

In the K-loop mutants of CK6, their ATPase activity was not affected. Thus, k and τ_w should be same for these mutants. δ and D_w also will be unaffected. δ will be determined by the structure of the motor and the MT-lattice structure, and D_w is determined by the temperature and the size (and the shape) of the motor. Then, Eqs. 1 and 2 predict that v and D will be same for all CK6-based K-loop mutants. The ATPase activity of KK6 was about 70% of CK6, indicating that k and τ_w of KK6 also will be about 70% of CK6. Assuming that δ and D_w will be the same for both conventional kinesin and KIF1A, Eqs. 1 and 2 indicate that v and D of KK6 will be about 70% and about 50% of CK6, respectively. These values agree well with the results shown in Figs. 3 D and E and 4 E and F.

We further tested this model by the perturbation to the ATPase cycle. Both the lower concentration of ATP and the addition of ADP slow down the ATPase cycle, but the mechanism of the inhibition is different. With the very low concentration of ATP, ATP binding becomes the rate-limiting step, resulting in the prolonged nucleotide-free, s-state (longer τ_s), whereas τ_w will not be affected. That is, the increase of the ATPase cycle time (= 1/k = τ_w + τ_s) is solely attributable to the increase of τ_s. On the contrary, the addition of ADP will inhibit the ADP release step and elongate τ_w, but will not affect τ_s. Namely, ATPase cycle time increases by the increase of the τ_w.

Eq. 1 predicts that v will decrease along with k, whereas Eq. 2 predicts that D will be affected by the changes of both k and τ_w. To delineate the effect of k and τ_w, we introduce the ratio of the motility parameters D/v as a parameter for the degree of stochasticity of the movement. From Eqs. 1 and 2, D/v is expressed as:

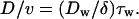3

In the limiting ATP condition, the inhibition of ATPase does not affect τ_w, thus D/v is expected to be unaffected by this perturbation. On the contrary, the addition of ADP will increase D/v through the increase of τ_w. By using the relation 1/k = τ_s + τ_w, this increase is expressed as the function of the ATPase turnover rate k as:

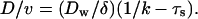4

Here, the ADP addition will not affect τ_s. Hence D/v will linearly increase against 1/k in this condition.

Actually, the ATPase activity was inhibited both by the limiting ATP condition and the addition of ADP, as expected from the Michaelis–Menten mechanism (Fig. 6B). In these conditions, the mean velocity (v) of CK6 movement measured by the single-motor motility assay proportionally decreased along with the ATPase turnover rate (k). The proportional coefficient was 1.6 ± 0.2 nm, giving the estimate for δ. This value is consistent with the previous estimate (10). This value and the D_w value measured in the above experiments gave the estimate for D_w/δ as about 25 nm/ms.

Fig. 6C shows the plot of D/v against 1/k. As predicted from Eq. 3, D/v value remained constant in the limiting ATP conditions, and τ_w was estimated to be about 7.5 ms. Thus, from the maximum ATPase turnover rate k_cat of CK6 (about 110/s), τ_s was estimated to be about 1.5 ms with saturating ATP. By substituting these estimates into Eq. 4, our model predicts the D/v value in the ADP-addition experiments as D/v = 25(1/k − 1.5). As shown in Fig. 5F, the measured values fit very well to this prediction.

These results collectively support our Brownian motor model in a quantitative manner.

Conclusion and Perspective

The combination of the biochemical and biophysical analyses of the K-loop mutants lead to three conclusions about the mechanism of the single-headed processivity. First, K-loop is the w-state-specific binding site of kinesins, and it interacts with the C-terminal E-hook of tubulin. Second, this K-loop–E-hook interaction as well as the basal binding level is essential for the single-headed processivity of kinesin-type motors. Third, the 1D diffusion in the w-state is the key mechanism for the single-headed processivity.

Furthermore, the values derived from these measurements fitted quantitatively well to our Brownian motor model. Interestingly, engineered, single-headed conventional kinesin also showed the highly processive and diffusional movement like KIF1A. This finding indicates that the single-headed processivity and the Brownian motor mechanism are not specific to KIF1A, but will be a common feature of kinesin-type motors.

As demonstrated, the key mechanism for the single-headed processivity lies in the 1D diffusion in the w-state. To allow such movement, the motor should be anchored to the MT in a way that the movement along the MT is free but that the movement away from the MT is restricted. Quite suggestively, the E-hook, an essential component of this anchoring, takes a highly flexible structure (21). This flexibility might allow the positional fluctuation of the motor within its reach, and the motor might dislocate forward and backward by hopping through the fluctuating E-hook like the vine swinging of Tarzan. Alternatively, the rapidly fluctuating E-hook along with the surface helices (H11 and H12) of tubulin might produce a uniform, negatively charged guide rail on the MT protofilament, along which the motor moves like a monorail with K-loop as the flange on the wheel.

In either model, the flexibility of the E-hook and the interaction between the K-loop and E-hook play an essential role in the anchoring of the motor to MT, which allows the 1D diffusion. This diffusional anchoring will enable the small monomeric motor to encompass the interval between the adjacent binding sites. The exact molecular or physical mechanism of this diffusional anchoring awaits future study.

Abbreviations

MT

microtubule

1D

one-dimensional

AMP-PNP

adenosine 5′-[β-γ-imido] triphosphate

w-state

weak binding state

s-state

strong binding state

MSD

mean square displacement