RNA folding energy landscapes

Abstract

Using a statistical mechanical treatment, we study RNA folding energy landscapes. We first validate the theory by showing that, for the RNA molecules we tested having only secondary structures, this treatment (i) predicts about the same native structures as the Zuker method, and (ii) qualitatively predicts the melting curve peaks and shoulders seen in experiments. We then predict thermodynamic folding intermediates. For one hairpin sequence, unfolding is a simple unzipping process. But for another sequence, unfolding is more complex. It involves multiple stable intermediates and a rezipping into a completely non-native conformation before unfolding. The principle that emerges, for which there is growing experimental support, is that although protein folding tends to involve highly cooperative two-state thermodynamic transitions, without detectable intermediates, the folding of RNA secondary structures may involve rugged landscapes, often with more complex intermediate states.

At the center of computational biology is the folding problem for proteins or RNA molecules: to predict the conformation having the global minimum energy from the monomer sequence. This problem is not yet solved. But even when it is solved, it will only give us a small fraction of the information we would like to have about biomolecule folding. We would also like to know how the folding process takes place, what are the folding routes, the folding thermodynamics and cooperativity, intermediate states, transition states, and conformational transitions. To understand these properties requires knowledge of more than just the single native conformation. It requires the full energy landscape (1–5): the free energies of all of the chain conformations as a function of the microscopic degrees of freedom of the molecule.

There are two practical reasons that it is important to know energy landscapes. First, knowledge of landscapes will be of benefit in designing faster and more robust computer methods for predicting native structures (6, 7). Second, a goal of computational biology is not just to predict native structures, per se, but to predict function. Ligand binding to proteins and RNA molecules, and catalytic mechanisms, are often more dependent on the conformations that are fluctuations away from the native structure than on the native conformation itself (8). To predict the fluctuations, we need energy landscapes.

Recent theoretical and experimental advances are beginning to go beyond native structures to shed light on full RNA folding energy landscapes (9–19). But so far, such landscapes have not yet been predictable from monomer sequences. There is one class of biomolecule conformations—RNA secondary structures—for which folding algorithms are fairly successful. A popular method for predicting the native secondary structures of RNA molecules has been developed by Zuker and others (20–25). In this paper, we describe a method for going beyond the prediction of such single points on landscapes. Our method predicts the full energy landscape for RNA secondary structures as a function of monomer sequence.

Predicting realistic energy landscapes for both proteins and RNA has been challenging because of severe computational limitations. All-atom simulations sample conformational space too sparsely (by hundreds of orders of magnitude) to characterize the full landscape. The other main approach has been lattice toy models (1–3) and other simplified treatments (26, 27), which can characterize the energy landscape completely, but only by sacrificing both atomic detail and the ability to treat realistically long sequences. Lattice models that have been used to explore complete energy landscapes are usually limited to chain lengths of ∼16–20 monomers in two dimensions. These folding landscapes so far have been mainly fictional, in the sense that they apply only to toy models and not to real monomer sequences such as lysozyme or ribonuclease.

We report here an approach, based on a polymer theory method that has recently been described in detail elsewhere (28, 29), in which we can retain a relatively high degree of realism and at the same time completely characterize the full energy landscape for RNA secondary structures having chain lengths up to at least 100–200 bases.

Overview of the Model.

The details of the model are given elsewhere (28, 29). But the basic idea is simple. RNA secondary structures involve stretches of helix, where two single-stranded chains run antiparallel to each other, separated by loops, bulges, and turns of various kinds and lengths, which we call intervening regions. Structures may involve any degree of branching. We aim to compute the partition function, which is the sum of Boltzmann factors over all possible ways and branching patterns in which the chain can be arranged into helices and intervening regions. Each Boltzmann factor accounts for the base pairing and stacking free energies for that particular configuration. The partition function is obtained by a matrix multiplication method, of the type that is used with the one-dimensional Ising model (30) or with the Zimm-Bragg theory of helix-coil transitions (31). The full chain partition function, Q(T), for a given set of intrachain contacts is a product of partition functions for short stretches of the chain (29):

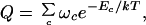where the sum is over all possible arrangements of contacts c, ω_c is the count of the number of conformations having a given arrangement of contacts, and the Boltzmann factor accounts for all of the contact interactions for the given set of contacts. The central idea is that ω_c is computed as a product of partition functions of component loops and helices (28):

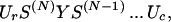where U_r = row(1, 1, 1, 1), U_c = col(1, 1, 1, 1), Y is a 4 × 4 matrix containing zeros and ones that insures that one stretch of chain has the right configuration of “outlet” (say, type m = 1, 2, 3, 4) to couple to the “inlet” of the next stretch of chain (say, type n = 1, 2, 3, 4). S is a 4 × 4 matrix that counts conformations having a coupling of type “nm ” (28).

These piecewise partition function matrices, S and Y, are computed in advance by lattice model enumerations. This approach does not rely on simplifying assumptions that are traditionally made about chain entropies (for example, that loop entropies are additive, or that loops are random flights that can be treated by Jacobsen-Stockmayer statistics, for example). Tests against exact enumerations show that the polymer theory captures the partition function with high accuracy (28, 29).

To use the method to predict experimental results requires a model for the energetics of base pairing interactions. We use the “Turner rules” for the enthalpies and entropies of the base stacking interactions in double helices (including noncanonical pairs) (32). We assume the stacking enthalpies and entropies are temperature-independent, and we assume pairing energies are zero when nucleotides are not stacked.

The model otherwise has only one parameter. Our method requires counts of the conformations under the many different possible constraints that could arise from all of the possible base-pairing arrangements. We obtain those counts from square lattice simulations. But the lattice model is two-dimensional and has only one degree of freedom per monomer whereas real polynucleotides are three-dimensional and have seven continuum dihedral degrees of freedom per monomer. However, Fig. 1 shows that a single multiplicative factor, μ, which is independent of chain length, converts the loop conformation counts obtained from the lattice simulations to those obtained from experimental measurements of RNA loop entropies.

Figure 1.

The loop closure probability P (y axis) for different loop lengths (x axis): experimental results (○) and two-dimensional lattice results (●). Experiments are from hairpin loop initiation parameters (32) using ln(P) = −ΔG/kT, where ΔG is the closure free energy. We assume ΔG is dominated by the loss of conformational entropy. The two-dimensional lattice results are from exact computer enumerations, where P is the ratio of conformation counts for the closed and open conformations. This factor that is needed to convert the lattice conformation count to the experimental data is approximately independent of chain length. For a self-avoiding chain on a two-dimensional lattice, there are three possible bond angles, which closely resemble three rotational isomeric states for each of the seven dihedral angle degrees of freedom per nucleotide. This simple relationship (one bond angle to seven angles) suggests the existence of a constant scaling factor μ to scale up the conformational count for realistic molecules. The numerical value of μ cannot be directly determined from the scaling in Fig. 1, because μ is defined for “loops” that do not contain any intra-loop contacts, whereas a loop measured in the experiment can contain unstacked (unstable) base–base contacts. We treat μ as a global constant for all loops because different loops, although possibly containing different details in geometry, share the same scaling relationship in chain conformational statistics, no matter how large the loop is and where the loop appears.

Tests of the Theoretical Method.

There are some basic tests an energy landscape model should pass. First, it must at least be a good folding algorithm; it should predict the point of global minimum, the native structure, on the energy landscape. In this regard, for the RNA molecules we tested, which are given in Fig. 2, our model has about the same level of accuracy as existing methods for predicting native RNA secondary structures (33, 34).

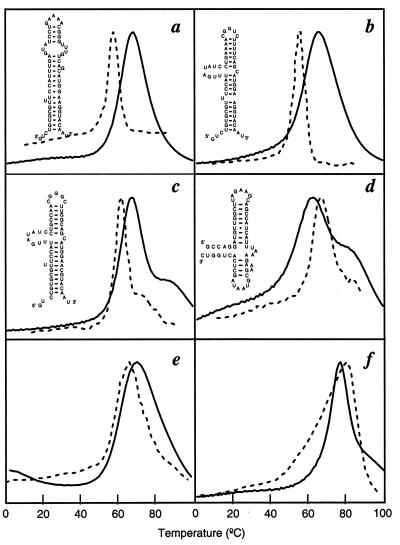
Figure 2.

Predicted (continuous lines) and experimental differential melting curves (dashed lines). a, b, c, and e show the results for α operon mRNA fragment and the variants in 100 mM (a, b, and c) or 1,000 mM (e) KCl with 10 mM Mops (33): G16-A72 (a); G36→U (b); AA44→CC, UU55→GG (c); and G16-U127 (e), with added nucleotides at the 3′ end: AU (a, b, and c). d and f show denaturation profiles for E. coli 23S rRNA fragment G1051-C1109 in 1 M KCl with 10 mM Mops (34) and E. coli 5S RNA in 1 M NaCl with 5 mM sodium phosphate and 1 mM EDTA (35), respectively. a and f are from calorimetric experiments, and b, c, and e are from UV absorbance experiments. Because our model energies are from Turner's rules, taken in 1 M NaCl, our model should in general overestimate the melting temperatures (T_m) for experiments in lower salt conditions. Because our model accounts only for the secondary structures, peaks in the experimental curves for the disruption of the tertiary structure (35) (f) were removed. The denaturation curve shows the heat capacity as a function of temperature. The heat capacity C(T) is obtained from the partition function Q(T) by using C(T) = ∂/∂T[kT²(∂/∂T)lnQ(T)]. The computer time scales with the chain length L as L⁴. For each temperature, the calculation of Q(T) and C(T) took 3 sec on an Intel Pentium Pro 200 computer for the 59-mer sequences (a–d), 30 sec for the 100-mer sequence, and 54-sec for the 120-mer sequence (f). We chose μ = e⁻² to give a best fit to the experimental curve in c, and used this value for all other calculations. Small variations in μ (e.g., μ = e^−2.5) cause only minor changes of the positions and shapes of the main and satellite peaks, but larger changes in μ lead to significant changes of the melting curves. Although the theory gives good predictions, given the simple approach, it is conceivable that the theory may differ with the experimental denaturation profiles in some details. Improvements can come from accounting for tertiary interactions, treating unpaired terminal nucleotides, and other refinements in the theory.

Second, an energy landscape model must predict more than just native structures; it must capture the rest of the space of conformations and their thermodynamic weights and must be able to predict denaturation thermodynamics. Fig. 2 shows the predictions for the denaturation profiles of six small RNA molecules that have no tertiary structures for which the melting thermodynamics are known (33–35). Some of the data shown are from heat capacities, which give a more direct test of the theory, and the rest are from absorbance measurements, which are related but not identical to the heat capacity curves we have computed. We include them because there are otherwise so few direct heat capacity measurements available and because the absorbance measurements tend to reflect the same general peaks and shoulders as would be seen in heat capacity measurements. We did not attempt to model tRNAs here for two reasons. (i) tRNAs contain pseudoknots, which are not treated in the current implementation of the theory. (ii) tRNAs have modified bases, for which there are no Turner rule energy parameters.

The theoretical predictions are not good enough to be within the experimental errors of the measurements, but they do appear to give qualitatively the peaks and shoulders. We think this model is a reasonable first approximation, on the following grounds. First, nucleic acid interactions depend strongly on salt concentration, but the only energies available to us, the Turner rules, came from measurements in 1 M salt. This may account for the overstability predicted by the model in most cases. Second, all of the quantities used in this model have been obtained by independent experiments, so no nonphysical parameter is used to fit the theory to the data. As with many statistical mechanical models, the relevant quantity for determining model errors is kT, where T = 300K, so errors of 10–20 degrees in melting points are small on this scale. The qualitative features of the denaturation profiles appear to be better predicted here than from more parameterized models (36). Third, because the model is physical, it is clear how to improve it: we could include tertiary contacts if appropriate energy parameters were available, include coaxial base stacking (37, 38) and terminal unpaired nucleotide and terminal mismatch energies, and perhaps include electrostatics. The present treatment illustrates both the successes of this level of approximation and the limitations.

Energy Landscapes and the Folding Pathways.

The main purpose of a model such as this is to relate microscopic conformations to macroscopic properties, such as the melting thermodynamics. In this section, we describe the structures that are predicted for a series of equilibrium melting experiments. No experiments are yet available to test this, as far as we know. We describe the results in terms of energy landscapes. Because a full high dimensional energy landscape is neither visualizable nor illuminating, Fig. 3 shows instead a “reduced” energy landscape, the free energy F(n,nn) = −kTlnQ(n,nn,T), where Q(n,nn,T) is the partition function, the count of all of the conformations that contain n native contacts and nn non-native contacts. F(n,nn) can be treated as a projection of the full landscape on the (n,nn) plane, assuming all of the other degrees of freedom are in thermal equilibrium and hence can be averaged out. A contact is called “native” if that particular hydrogen-bonded base pair exists in the native structure, and “non-native” otherwise.

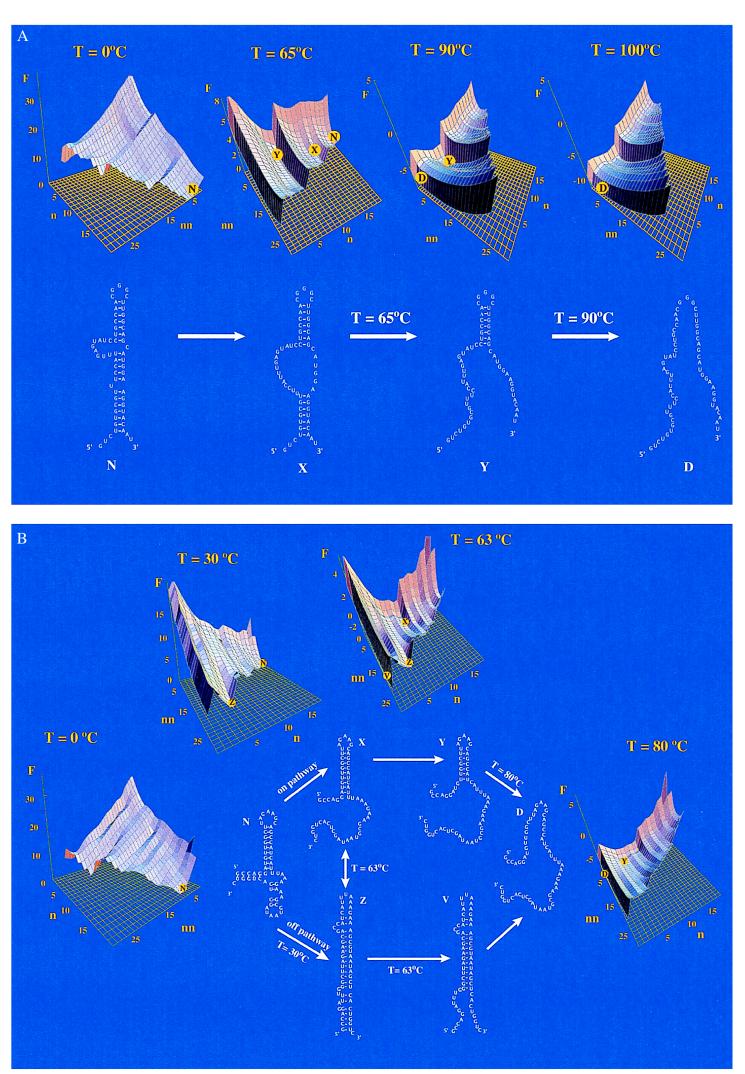
Figure 3.

The energy landscapes F(n,nn) vs. Temperature T (in °C) for (A) mutant α mRNA fragment (Fig. 2c) and (B) E. coli 23S rRNA fragment (Fig. 2d). F(n,nn) is the free energy for a state with n native contacts and nn non-native contacts, where the native and non-native contacts are defined according to the native structure N. The free energies (in kcal/mol) are relative to the native states. Under native conditions, the number of non-native contacts need not equal zero, because loops can bump into the chain in ways that involve no stable contact. Stable states are valleys, highlighted by the symbols on the energy landscapes.

The main purpose of this particular kind of plot is to explore a question that is motivated by a longstanding issue in protein folding. The question is whether folding intermediates are “on-pathway” or “off-pathway.” This question can be asked of either the kinetics or of the thermodynamics. Here we focus on the thermodynamics. The distinction is as follows. For kinetics, we would need to define a reaction coordinate. We would then ask for the time sequence of conformations that follow a jump either to folding or unfolding conditions.

For thermodynamics, we would only need to define an order parameter, not a reaction coordinate. An order parameter is just some structural or energetic measure of the “nativeness” of the protein. An order parameter need not also include a measure of “kinetic closeness” of one conformation from another that is necessary for a reaction coordinate. We focus on a series of equilibrium experiments, each performed at a different temperature. At each temperature, we compute the equilibrium ensemble of conformations, and whatever average structural property is of interest. In the present work, we have not considered reaction coordinates or any other aspect of kinetics. An assumption is often made that the kinetics time series of conformations would closely mimic the equilibrium series (39), but we do not take up that question here.

We define an on-pathway intermediate as a stable state having few non-native contacts. In contrast, an off-pathway intermediate can have many non-native contacts, but will have few native contacts.

Landscapes provide insights into cooperativity in biomolecule folding. The shape of the landscape can be characterized by the minima, which correspond to stable intermediates, and the maxima or barriers dividing them. As T changes, the shape of the landscape changes because of the competition between enthalpy and entropy.

We find stable intermediate states for both the mutant α operon mRNA 59-nucleotide fragment shown in Figs. 2c and 3A and the Escherichia coli 23S rRNA 59-nt fragment shown in Figs. 2d and 3B. But the landscapes of the two molecules (Fig. 3 A and B) are clearly different. The intermediates of the mutant α operon mRNA fragment are on-pathway in the sense that the folding process involves the sequential formation of the native helices, as a function of temperature. No non-native helices are formed. The thermodynamic “pathway” is indicated by partial degrees of “unzipping” of the native helices from the middle (see Fig. 3A). The cooperativity can be described by a “stuck zipper” model, where the zipping gets stuck in states X and Y (defined in Fig. 3A), and there is little population of other partially zipped states. Because state X and state Y are separated by a free energy barrier, the transitions between the stuck states are “two-state,” resembling first-order phase transitions such as boiling and freezing in macroscopic systems.

On the other hand, the E. coli 23S rRNA fragment shows a much more complex transition than is predicted for the α mRNA fragment (see Fig. 3B). For example, at T = 30°C, two almost equally stable conformations (N and Z) coexist. The unfolding of N involves two routes: one set of intermediates is on-pathway and the other is off-pathway. Fig. 3B shows that heating the native RNA leads not just to a partial unzipping (the on-path intermediate), but also to a highly helical state having even more contacts than the native structure but involving weaker interactions. Off-pathway intermediates have been previously predicted in other RNA models (40), where a “molten” phase was found to exist before the main unfolding occurs.

Experiments show complex folding cooperativity in RNA tertiary structures. Mg²⁺ appears to stabilize tertiary structures (41, 42). Folding pathways have been found to involve multiple cooperative (two-state) or noncooperative transitions, depending on the salt concentrations (43–47).

Density of States.

Fig. 4 shows the predicted density of states g(E), which is the number of conformations at each energy level. The power of the present theoretical method is that it can give the density of states over the whole landscape, a quantity that is not readily obtainable by sampling and trajectory-based simulations, such as Monte Carlo or molecular dynamics. Even the rarest of states can be explored; Fig. 3 shows the probabilities of states over a range of more than 100 orders of magnitude in population.

Figure 4.

The density of states g(E) for α mRNA fragment (Fig. 2c) (blue) and E. coli 23S rRNA fragment (Fig. 2d) (red), normalized to g(E_min) = 1.

The density of states reveals information about the shape of the energy landscape. The left side of Fig. 4 describes the lowest energy states. Because g(E) is small on the left, it indicates that there are very few low-energy states. The right side indicates that there are very many high energy states; these are the denatured conformations. Taken together, it implies a general funnel-shaped landscape. At a more subtle level, if the left side of the figure were to be concave upwards, it would imply that the native state would be separated by an energy “gap” from the denatured states. Such a concave shape would indicate a paucity of low energy “trap” conformations and that the native energy well is much deeper than other energy wells. But if anything, Fig. 4 is slightly concave downwards on the left side, implying many low energy non-native states, which indicates that these RNA folding energy landscapes are quite bumpy and rugged.

In this regard, the model predicts that RNA folding may be quite different than protein folding. Proteins tend to have energy gaps, and a single native state that is much more stable than alternative conformations. Here, the prediction is that RNA molecules, at least those having predominantly secondary structures, may have many low energy states and bumpy landscapes. This appears to be consistent with experiments (9, 11, 15, 16, 42) and indicates that kinetics and metastability may play a greater role in the properties of RNAs than for proteins (1–5). Perhaps evolution has not optimized RNA secondary structures to fold uniquely, to be very stable, or to fold quickly.

Higgs has also predicted multiple low energy states for some RNA sequences (48, 49). His density of states, however, is not comparable to ours, because it counts only secondary structures, rather than conformations. His observation of a Gaussian function is therefore not in conflict with our non-Gaussian density of states. Some protein models also predict non-Gaussian densities of states (50). Our g(E) shown in Fig. 4 is remarkably linear. Because 1/T = ∂S/∂E = k∂lng(E)/∂E, the slope of our density of states curve gives the temperature of the main melting transition. For example, for the mutant α operon mRNA 59-nt fragment, the slope is 0.68 mol/kcal, corresponding to a transition temperature (k slope)⁻¹ − 273 ≃ 65 (°C).

We have described a method for predicting energy landscapes for RNA molecules. It predicts that RNA secondary structures have a wide variety of cooperative behaviors, including one-state and two-state transitions, stable intermediate states, some of which are on-path (monotonically becoming more native-like) and some of which are off-path (dominated by non-native contacts). Our approach is presently limited to the prediction of equilibrium folding for the secondary structures of RNAs and of single-stranded DNA molecules. But because it treats increasingly complex chain conformations by a systematic hierarchy of equations, the present approach may ultimately be useful also for more complex tertiary structures in proteins and RNAs.