Composite Module Analyst: identification of transcription factor binding site combinations using genetic algorithm

Abstract

Composite Module Analyst (CMA) is a novel software tool aiming to identify promoter-enhancer models based on the composition of transcription factor (TF) binding sites and their pairs. CMA is closely interconnected with the TRANSFAC^® database. In particular, CMA uses the positional weight matrix (PWM) library collected in TRANSFAC^® and therefore provides the possibility to search for a large variety of different TF binding sites. We model the structure of the long gene regulatory regions by a Boolean function that joins several local modules, each consisting of co-localized TF binding sites. Having as an input a set of co-regulated genes, CMA builds the promoter model and optimizes the parameters of the model automatically by applying a genetic-regression algorithm. We use a multicomponent fitness function of the algorithm which includes several statistical criteria in a weighted linear function. We show examples of successful application of CMA to a microarray data on transcription profiling of TNF-alpha stimulated primary human endothelial cells. The CMA web server is freely accessible at http://www.gene-regulation.com/pub/programs/cma/CMA.html. An advanced version of CMA is also a part of the commercial system ExPlain™ (www.biobase.de) designed for causal analysis of gene expression data.

INTRODUCTION

Novel high-throughput methods, such as microarrays, allow generation of massive amounts of molecular biological data. Using various sophisticated statistical analyses of the microarray data, genes are revealed whose change of expression is associated with a particular cell type, tissue, response to certain extracellular signals or with particular disease. However, the observed changes often represent just an ‘echo’ of the real molecular processes within gene regulatory networks of the cells. Nowadays, with full confidence, we can say that the key component of the regulatory network of the cell is regulation of gene expression by transcription factors (TFs). In order to understand molecular mechanisms of gene regulation we should be able to identify binding sites for TFs important for all those biological processes. Knowledge collected in the TRANSFAC^® database (1) can be used to find putative TF binding sites and their effector genes in silico. Positional weight matrices are used to search for putative TF binding sites. This approach was applied intensively in the last years for the analysis of regulatory regions of many different functional classes of genes, for instance, globin genes (2), muscle-specific and liver-specific genes (3,4), and cell cycle-dependent genes (5).

Despite this success, it becomes clear that gene regulation is accomplished by specific combinations of TFs rather than by single factors alone. Knowledge about functional combinations of TF binding sites (composite modules, CMs) was used before in a number of approaches: for the identification of muscle-specific promoters (3), promoters of liver-enriched genes (6), of yeast genes (7), of immune response-specific genes (8–11). Such knowledge on functional combinations of TF binding sites [composite elements (CE)] is being collected in the TRANSCompel^® database for many years (12,1). But still this knowledge is limited and often restricted to simple site combinations such as pairs or triplets of TF binding sites. Several methods for automatic identification of functional CMs were proposed during the last years ranging from assessment of simple pairwise combinations, e.g. in the promoters of genes regulated during cell cycle (5) and antibacterial defense response (13,14), to applications of various statistical and machine learning techniques to identify more complex modules [ClusterScan and CMFinder (15,16); TOUCAN system (17,18)]. Still, analysis of long regulatory regions remains a challenge.

We developed a new method, the Composite Module Analyst (CMA), for identification of complex CMs in long regulatory regions. CMA applies a novel approach for defining a promoter model based on composition of single TF binding sites as well as their pairs located inside local regulatory domains (corresponding to enchancer/silencer sub-regions). We employ a multicomponent fitness function described in our recent paper (19) for selection of the promoter model from a population which fits best to the observed gene expression profile. CMA is made freely available through the web, where it can be used for online analysis of sets of promoters of co-regulated genes as well as for analysis of any sets of regulatory sequences including collections from ChIP–chip experiments.

ALGORITHM

CMA builds a promoter model which consists of one or several composite regulatory modules. The structure of the model and the algorithm applied to build the models is described in detail in our recent paper (19). Here we present just a short outline of the algorithm and point on some recent improvements.

Composite modules

Each CM can be represented as duplet (M,Ψ), where M is a set of positional weight matrices (PWMs) included in the module and Ψ is a set of rules: length of the module (w); number of individual PWMs (K) and number of considered best matches ${\kappa }^{\left(k\right)}$ of them; number of pairs of PWMs (R) and number of considered best pairs of matches ${\kappa }^{\left(r\right)}$; mutual location and orientation of several PWM matches to each other, parameters of the matrix cut-offs ($q_{\text{cut-off}}^{\left(k\right)}$ and $q_{\text{cut-off}}^{\left(r\right)}$), and other parameters of the module.

Once a CM is defined, it can be applied to classify any nucleotide sequence. For this, we use Match™ to search for potential TF sites in the sequence by applying the PWMs from M. After that, in each sliding window x of the length w, the program selects the predefined maximal number of the best matrix matches and checks if the found sites obey the cut-offs, distance and orientation rules given in Ψ. For each window position we calculate a normalized composite score value, cms(x), using the following equation [which is a modified version of the score presented in Ref. (19)]:

$$cms\left(x\right)=\begin{array}{c}[{\sum }_{k=1,K_i}{\varphi }^{\left(k\right)}\times {\sum }_{j=1}^{{\kappa }^{\left(k\right)}}{q}_j^{\left(k\right)}\left(x\right)\\ \frac{+{\sum }_{r=1,R_i}{\varphi }^{\left(r\right)}\times {\sum }_{i=1}^{{\kappa }^{\left(k\right)}}\left(q_{1,i}^{\left(r\right)}\left(x\right)+q_{2,i}^{\left(r\right)}\left(x\right)\right)]}{\text{Max}\left(cms\right)},\end{array}$$ 1

where $q_j^{\left(k\right)}\left(x\right)$ is the score of j-th match of the k-th PWM and $q_j^{\left(k\right)}\left(x\right)>q_{\text{cut-off}}^{\left(k\right)}$; and $q_{1,i}^{\left(r\right)}\left(x\right)$ and $q_{2,i}^{\left(r\right)}\left(x\right)$ are scores of two sites in a pair r and $q_{1,i}^{\left(r\right)}\left(x\right),q_{2,i}^{\left(r\right)}\left(x\right)>q_{\text{cut-off}}^{\left(r\right)}$ and the distance between these sites in the pair: $d_{\text{min}}^{\left(r\right)}<d^{\left(r\right)}<d_{\text{max}}^{\left(r\right)}$; Max(cms)—is the maximal possible value of cms (i.e. all matches of all matrices and all pairs of matrices are found and the scores of all sites are = 1.0).

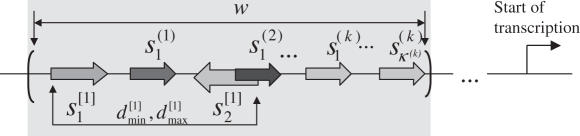
So, if cms(x) is higher then a predefined threshold cms_cut-off the program reports a match of the CM to the sequence (Figure 1).

Figure 1.

A schematic representation of a match of a CM in a particular promoter. Several TF sites and pairs of TF sites are found in a sequence window of the length w, which is located in an upstream region of a given gene.

Promoter model

CMA builds a promoter model in the form of a Boolean function θ that joins in one predicate several logical outputs of CMs of different types, each in its own window. So, for a given sequence S, the promoter logical-score ps can be computed as follows:

$$ps\left(S\right)=\theta (b1,b2,\dots b\text{m}),$$ 2

where b_i are the (0,1) outputs of independent CMs of m different types (i = 1, 2, … , m). To compute b_i for the CM of i-th type we calculate cms(x) for all windows x in the sequence S, find the maximal composite score and compare it with a predefined cut-off (the cut-off can be different for each i-th CM):

$$b=\{\begin{array}{ll}1,& \text{if }{\displaystyle \underset{x\in S}{\text{max }}}\left(cms\left(x\right)\right)\ge {\mathit{cms}}_{\text{cut-off}}\\ 0,& \text{otherwise}\end{array}.$$ 3

Finally, if, ps(S) = 1 we consider that sequence S matches the defined promoter model.

In the current CMA implementation we consider a family of the Boolean functions of the following form:

$$\begin{array}{r}\left(b_1^1\text{ OR }{b}_2^1\dots \text{OR }{b}_{m1}^1\right)\text{ AND }(b_1^2\text{ OR }{b}_2^2\dots \text{ OR }{b}_{m2}^2)\\ \dots \text{ AND }(b_1^g\text{ OR }{b}_2^g\dots \text{ OR }{b}_{m_g}^g),\end{array}$$

which is a series of g conjunctions, each is a series of m_g disjunctions. In addition, the logical NOT can be applied to the individual components b_i.

In order to obtain a ‘smooth’ score of a promoter model match we apply a fuzzy logic approach to the values obtained with the Boolean function θ, as it is described in details in Ref. (19) and compute the fuzzy promoter score fps.

Genetic algorithm

The parameters of the promoter model are found by an optimization strategy based on an implementation of genetic algorithm. The composite promoter model best fitting the given data on gene expression is constructed using a complex fitness function described in Ref. (19). The algorithm takes as input two sets of promoters (the set of promoters of differentially expressed genes—group A; and a set of promoters of genes whose expression does not differ significantly between experiment and control—group B) or a set of promoters and the relative expression values (usually, ‘log ratio’ or ‘fold change’) assigned to the corresponding genes. The genetic algorithm proceeds over several iterations of generation of ‘populations’ of models, random ‘mutations’ of model parameters and selections of models characterized by highest values of the fitness function. The output of CMA is the model providing the best discrimination between the two promoter sets at the last iteration.

WEB SERVER: INPUT AND OUTPUT

The CMA web server is freely accessible at http://www.gene-regulation.com/pub/programs/cma/CMA.html.

The CMA interface takes the following input:

1. Set of ‘POSITIVE’ sequences—subjects for identification of a common promoter model (group A, see Genetic Algorithm). The set must contain several sequences in FASTA or EMBL format. The length of the sequences is generally not limited, but it is recommended not to exceed 20 kb per sequence. Sequences of one group should be of a similar length in order to avoid bias towards longer sequences, but not necessarily of exactly the same length since the algorithm computes each CM in a sliding window along the sequences.

2. Set of ‘NEGATIVE’ sequences—background set (group B, see Genetic Algorithm). In the case of microarray gene expression data one can use the NC genes (whose expression has not changed in the experiment) as background set. Otherwise, randomly chosen promoters, various genomic non-promoter sequences or randomly generated sequences might be taken. We provide a default set consisting of 100 housekeeping gene promoters [based on the paper (20)], each of 1.1 kb length (−1000 to +100 around TSS).

3. Profile—a predefined set of PWMs with given cut-offs. A user can choose among several profiles contained in the public version of the TRANSFAC^® rel. 6.0 database: ‘all’—the complete library of matrices including matrices for various taxa; ‘vertebrate’—PWMs for TFs in vertebrates; ‘non-redundant’—selected matrices for vertebrate factors with one matrix per factor family; tissue-specific profiles that include matrices for TFs specifically active in particular tissues as well as other profiles.

The web interface allows to configure a number of CMA search parameters. CMs can be constrained with respect to the number of binding site matrices, number of matrix pairs and distance between sites within the pairs, where counts of matrices and pairs as well as distances can be specified approximately through triplets of minimal, maximal and average values. This allows to find better models according to the given range of parameters. On the other hand, the user can also require CMA to optimize site distances and orientation considered in a model through the ‘optimize distance’ and ‘consider orientation in pair’ switches of the interface.

The ‘Boolean promoter model’ set of options allows to define the number of modules in the promoter model, their window size and the structure of the Boolean function (by defining the maximal number of groups—conjunctions and the maximal number of modules in each conjunct). The ‘Allow repressing module’ switch enables CMA to include the NOT operator into the function.

The search for an optimal model can be directed with a set of ‘Genetic Algorithm’ options. While the population size and the number of iterations are set to defaults of 10 and 10, we rather recommend to use at least 100 iterations and a population of 50 chromosomes, which however takes longer time to compute. By choosing parameters of restricting either FP (false positives) or FN (false negatives) users can try to direct the algorithm to identify promoter models with the given restriction of the corresponding errors rate. For instance, by defining ‘Restrict FN to 0..0.1’ the user directs the algorithm towards identifying promoter model with very low false negative rate—very sensitive model (so, it will give matches practically in any sequence of your positive set, though might be not very specific and give matches in the background set as well).

Setting of the fitness function components provides the possibility to change the relative weighting of five components in the fitness function. Detailed description of the components is given in the recent publication (19). Here we just mention them:

• R—regression value;

• T—Student's t-test value;

• E—specificity and sensitivity value;

• N—normality index;

• P—penalty on the complexity of the mode.

The fitness function is defined as linear combination of these components with the specified relative weights:

$$Z=\frac{\left(aR+bT+cE+dN+eP\right)}{\left(a+b+c+d+e\right)}.$$ 5

The weights a, b, c, d and e can be modified by the user through the CMA web interface.

The output of CMA web server is one promoter model which was found by the genetic algorithm as best discriminating the ‘POSITIVE’ and ‘NEGATIVE’ sets of sequences (got the maximal value of the fitness function). Let us consider the output in more detail on the example of analysis of real gene expression data.

APPLICATION EXAMPLE

An extensive testing of the algorithm on simulated and on real data has been performed earlier (16,19). On the simulated data we have shown that the algorithm is able to reveal back correctly the combinations of sites that were artificially introduced in the random sequences (16,19). On the real data—a set of T-cell specific genes known to be regulated by the pair of TFs NF-AT/AP-1, we have confirmed that CMA algorithm is able to reveal statistically significant CMs that have biological sense for the tested gene set (19). In the current paper we present results of applying CMA to the analysis of microarray gene expression data.

We analyzed microarray data on transcription profiling of TNF-alpha stimulated primary human endothelial cells. The gene expression data were taken from the recent paper (21). It is generally known that stimulation of the cells by TNF-alpha signal triggers activation of several signaling pathways, which in turn lead to the activation of specific set of TFs including such factors as NF-kappaB and AP-1 that provide the transcriptional regulation of certain set of target genes. The detailed mechanisms of the target gene regulation still largely unknown. For instance, it is not clear which TFs are involved in providing induction of gene expression in contrast to repression.

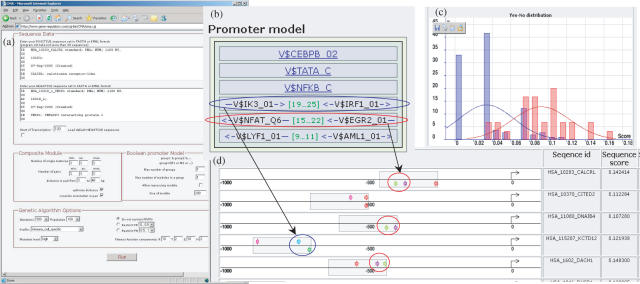
In order to discover the mechanisms of the gene regulation under TNF-alpha stimulation we use CMA web server and compare promoters of 30 top up-regulated genes to the promoters of 106 most down-regulated genes (see Example 1 on the website http://www.gene-regulation.com/pub/programs/cma/example.html). The CMA web interface and the screenshots with the results are shown on the Figure 2. One can see that CMA tool, after 500 iterations of the genetic algorithm, has revealed a CM consisting of three single matrices and three matrix pairs that provide significant discrimination between promoters of up- and down-regulated genes. It is interesting to see that the CMA algorithm selects matrices for C/EBP and NF-kappaB TFs, known as coordinators of synergistic effect of several cytokines including TNF-alpha (22). Among pairs selected by the algorithm into the promoter model there is NF-AT/EGR pair, which is a known type of CEs well documented in TRANSCompel^® database. It is known that NF-AT/EGR CEs provide enhanced expression of specific genes through the mechanisms of synergetic interaction between factors upon T-cell activation [see e.g. (23)]. Two other pairs IK3/IRF1 and LYF1/AML1 seems to represent yet unknown types of CEs. It is tempting to speculate that the revealed CMA promoter model represents a set of requirements for the promoters of the genes to be up-regulated upon stimulation of the cell by TNF-alpha. And the structure of the promoter model provides a clue for understanding the mechanisms of such regulation through binding of various TFs to their adjacent binding sites on DNA and synergistic interaction between these TFs.

Figure 2.

CMA web interface and results of identification of the CM discriminating promoters of up-regulated genes from promoters of down-regulated genes upon TNF-alpha stimulation of primary human endothelial cells. (a) CMA web interface; (b) representation of the identified CM that consists of three single weight matrices and three pairs of matrices. The distance limits orientation of the sites in the pairs are schematically shown. (c) Two histograms of the fuzzy promoter score (fps) in the promoters of up-regulated genes (red) and in down-regulated genes (blue); (d) representation of TF sites found in the windows that correspond to the maximal score of the match of the CM in the promoters. Marked are identified NF-AT/EGR2 site pairs (red) and IK3/IRF1 site pairs (blue).

CONCLUSION

In this paper we describe the web server of CMA—a novel tool for analysis and interpretation of gene regulatory regions. The CMA tool identifies CMs—stable combinations of TF binding sites that are shared by the most of the co-regulated promoters. It is generally accepted that such modules are responsible for a function-specific regulation of transcription.

Several tools have been published, before that consider combinatorics of TF binding sites. Among them, there are tools that deal with ab initio identification of pairs of motifs in DNA sequences, such as BioProspector (24), Co-Bind (25), MITRA (26) and dyad search (27). Such approaches generally suffer from low signal-to-noise ratio of the real TF binding motifs in the long regulatory sequences. Application of collections of a priori known patterns (such as large collection of TF binding PWMs in TRANSFAC^®) can help to identify meaningful combinations of TF binding sites. Several approaches, mentioned in Introduction, are making attempts towards this direction of study. In comparison with most of the previously published tools of this type, CMA has several advantages, such as (i) optimization not only of the matrix sets, but also of cut-off values for each matrix; (ii) analysis of large regulatory regions; and (iii) search for pairs of matrices, selecting best distance and orientation.

Testing CMA on simulated and real data has shown (i) it is able to correctly reveal CMs that are overrepresented in the set of sequences; (ii) it can be used to analyze data and propose factor combinations that are playing key roles in transcriptional regulation in the given biological context. Application of this approach to the analysis of microarray gene expression data is very promising. The CMA is implemented now as a part of the commercial software system ExPlain™ that provides a wide range of tools, such as Match™ (28) and ArrayAnalyzer™ (1), and databases for causal interpretation of gene expression data.