Skip to main content
PMC home page
Nucleic Acids Research logoLink to Nucleic Acids Research
. 2006 Jul 14;34(Web Server issue):W700–W703. doi: 10.1093/nar/gkl042

ModelTest Server: a web-based tool for the statistical selection of models of nucleotide substitution online

David Posada 1,*
PMCID: PMC1538795  PMID: 16845102

Abstract

ModelTest server is a web-based application for the selection of models of nucleotide substitution using the program ModelTest. The server takes as input a text file with likelihood scores for the set of candidate models. Models can be selected with hierarchical likelihood ratio tests, or with the Akaike or Bayesian information criteria. The output includes several statistics for the assessment of model selection uncertainty, for model averaging or to estimate the relative importance of model parameters. The server can be accessed at http://darwin.uvigo.es/software/modeltest_server.html.

INTRODUCTION

Models of nucleotide substitution play a significant role in the study of DNA sequences. The use of one or another model can change our impressions regarding the evolution of a given genomic region, and therefore influence the conclusions derived from its analysis (1–3). Hence, the use of a given model needs to be properly justified.

The program ModelTest (4) is a widely used standalone application for the selection of models of nucleotide substitution. This program implements different statistical frameworks for model selection, including hierarchical likelihood ratio tests (hLRT), the Akaike Information Criterion (AIE) and the Bayesian Information Criterion (BIC). Currently the ModelTest program can run on computers with different operating systems including Mac OS (with graphical user interface), Windows (DOS console) and UNIX-like (command line). To unify these different implementations, and to make the program more accessible to a wider range of researchers, the ModelTest server offers a single site for the selection online of models of nucleotide substitution.

MODELTEST SERVER

Server implementation

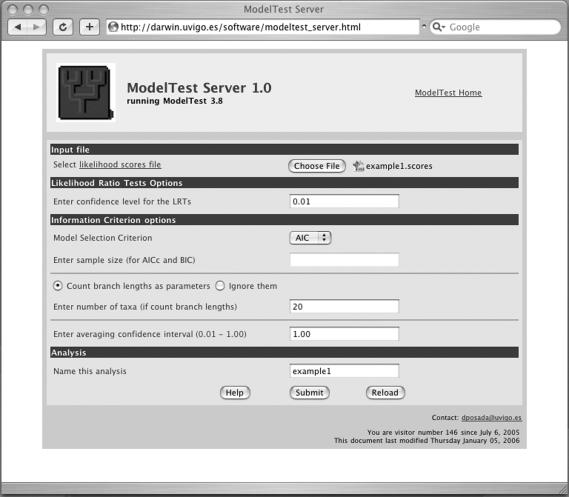
The ModelTest web server starts with an HyperText Markup Language (HTML) form where the user can specify the input file and several options for the analysis (Figure 1). Several JavaScript functions are included in this page to validate the input and to enable or disable several options according to the selections made by the user. All the user data are submitted to a Common Gateway Interface (CGI) written in Perl that organizes the analysis. This CGI program uploads the input file, executes the program ModelTest according to the user specifications, and writes the output in HTML in a new browser window.

Figure 1.

Figure 1

Open in a new tab

The web page for the ModelTest server, with the options used for the analysis of the example dataset.

Analysis options

The capabilities of the server are the same as those in the program ModelTest. The user needs to specify a text input file containing the likelihood scores for 56 models of DNA substitution. This file is most easily obtained by executing in PAUP* (5) a command script that can be obtained from the help page of the server. Further instructions can be found in the program manual (also available from the help page of the server) or in (6,7).

The only option within the hierarchical likelihood framework (4,8,9) is the statistical confidence level. For each individual likelihood ratio test, this level is set by default to 0.01, but the user can specify any value. The user should note that five or six likelihood ratio tests will be performed, increasing the type I error, so using a 0.01 individual test level will be more or less equivalent to a Bonferroni correction to maintain a global 0.05 confidence level.

The user can choose between three information criteria: the AIC (10–12), an AIC corrected for small sample sizes (AICc) (13,14) and the BIC (15). Users are referred to references (1–3,13,14,16–20) for background on these methods. If the AICc or BIC model selection options are selected, then the user needs to indicate also the sample size corresponding to the DNA sequence alignment from which the model likelihoods were obtained. This is a difficult choice, because the concept of sample size of a sequence alignment has yet to be developed. Here, most people uses the length of the alignment as a surrogate for sample size, although other options exist (2,21). Furthermore, because model likelihoods are conditional on a given DNA sequence alignment and a tree topology, branch lengths should be considered parameters of the models as well, which is the option selected by default. In this case the user needs to specify the number of sequences, so the program can automatically calculate the number of branch length parameters. The inclusion of branch lengths as parameters will not change the AIC or BIC ranking of the models, as its number is a constant for all models, but might change the AIC differences (2). Alternatively, the user can decide to ignore branch lengths and not include them as model parameters. In addition, the user can select whether all models are included in the model averaging calculations, or just a given set of models is used according to their cumulative information weight. Finally, the user can indicate a name for the analysis.

The server offers a help page where all the options are explained in detail, as well as a link to the script of commands for PAUP* and to the ModelTest PDF manual.

Output

Once the user sends the data to the server by pressing the submit button, the output page opens up in a new window in a few seconds (Figure 2). The output includes a header indicating the job number, the title of the analysis, the submission date, the IP address of the local computer and the input file name. After this header, the standard output of ModelTest will appear. This output includes two model selection frameworks, the hLRT and one of the three information criteria: AIC, AICc or BIC. The hLRT section includes the sequence of likelihood ratio tests performed, a description of the model selected including parameter estimates, and a set of commands that can be appended to a NEXUS file (22) with the sequence alignment in order to implement this model in PAUP* automatically. The information criterion section includes a full description of the model selected according to the chosen criterion, a set of PAUP* commands to implement this model, a ranking of all models according to their weight for the assessment of model selection uncertainty, and a table including parameter importance's and model-averaged estimates of model parameters.

Figure 2.

Figure 2

Open in a new tab

Output window of the ModelTest server corresponding to the analysis of the example dataset.

EXAMPLE DATASET

The example file ‘example1.nex’ includes an alignment of 20 DNA sequences 1000 nt long, simulated according to the coalescent (23) with an effective population size of 1000 and a mutation rate of 2 × 10−5 substitutions per site per generation. The model of nucleotide substitution used was the Hasegawa–Kishino–Yano model (HKY) (24) with unequal base frequencies (fA = 0.4, fC = 0.2, fG = 0.1, fT = 0.3), a transition/transversion ratio of 2, and rate variation among sites (25) [alpha (α) shape of the gamma (Γ) distribution = 0.5].

This example dataset was loaded into PAUP*, and upon execution of the ‘modelblockPAUPb10’ script, the file ‘example1.scores’ was obtained. This file, as well as the original DNA alignment, is available from the help page of the ModelTest server. The file ‘example1.scores’ was then analyzed with the ModelTest server (Figure 1: input file =example1.scores; confidence level for the LRTs = 0.01; model selection criterion = AIC; counting branch lengths as parameters, with number of taxa = 20; averaging confidence interval = 1).

The output of the server for this dataset, partially represented in Figure 2, is included as Supplementary Data. The output starts with the hLRT section, indicating the details for the six sequential LRTs performed. The model selected is HKY + Γ, which corresponds exactly with the model of nucleotide substitution used to simulate the original sequence alignment. The output includes the parameter estimates obtained in PAUP*, and set of PAUP* commands to implement this model. In the AIC section, the output indicates that this criterion also selects HKY + Γ as the best model among the 56 candidates. Again, the output includes the parameter estimates obtained in PAUP*, and a set of PAUP* commands to implement this model. Next we can see a table where models have been ordered according to their Akaike weights. Here, the best model only accumulates 20.75% of the total weight, and the best 12 models are needed to accumulate more than 95% of the total weight (96.22%). This indicates that there is quite a bit of model selection uncertainty, suggesting that several models could be used to make inferences from this dataset. The last table in the output indicates the importance (0–1) of the different parameters and the model averaged estimates. We can see that considering unequal base frequencies are very important (importance = 0.9935), that considering certain substitution types (AG or CT) is more important than considering others and that rate variation can also be important [alpha (G) = 0.5849]. The model-averaged estimates provide us with estimates obtained by averaging all 56 models. In general, they tend to be quite similar to those obtained under the best-fit model (HKY + Γ).

CONCLUSIONS

The ModelTest server is a useful online application for the selection of models of nucleotide substitution that will facilitate the execution of ModelTest to a wider range of users across many different platforms. The program includes three different frameworks for model selection and offers a serious of tools for the assessment of model selection uncertainty and model averaging.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR online

Acknowledgments

The author wishes to thank Keith Crandall, Marcos Pérez-Losada, Rafael Zardoya, Federico Abascal and Thomas Buckley for testing the web server, and Jerry Johnson and an anonymous reviewer for comments that have improved this manuscript. This work has been supported by grant BFU2004-02700 of the Spanish Ministry of Education and Science and by the ‘Ramón y Cajal’ initiative of the Spanish government. Funding to pay the Open Access publication charges for this article was provided by the Spanish Ministry of Education and Science.

Conflict of interest statement. None declared.

REFERENCES

  • 1.Sullivan J., Joyce P. Model selection in phylogenetics. Annu. Rev. Ecol. Evol. Syst. 2005;36:445–466. [Google Scholar]
  • 2.Posada D., Buckley T.R. Model selection and model averaging in phylogenetics: advantages of Akaike Information Criterion and Bayesian approaches over likelihood ratio tests. Syst. Biol. 2004;53:793–808. doi: 10.1080/10635150490522304. [DOI] [PubMed] [Google Scholar]
  • 3.Johnson J.B., Omland K.S. Model selection in ecology and evolution. Trends Ecol. Evol. 2003;19:101–108. doi: 10.1016/j.tree.2003.10.013. [DOI] [PubMed] [Google Scholar]
  • 4.Posada D., Crandall K.A. Modeltest: testing the model of DNA substitution. Bioinformatics. 1998;14:817–818. doi: 10.1093/bioinformatics/14.9.817. [DOI] [PubMed] [Google Scholar]
  • 5.Swofford D.L. PAUP*: Phylogenetic Analysis Using Parsimony (*and Other Methods) 2000. Version 4.0b10. Sinauer Associates, Sunderland, Massachusetts.
  • 6.Posada D. Selecting models of evolution. In: Vandemme A., Salemi M., editors. The Phylogenetic Handbook. Cambridge, UK: Cambridge University Press; 2003. pp. 256–282. [Google Scholar]
  • 7.Posada D. Using Modeltest and PAUP* to select a model of nucleotide substitution. In: Baxevanis A.D., Davison D.B., Page R.D.M., Petsko G.A., Stein L.D., Stormo G.D., editors. Current Protocols in Bioinformatics. John Wiley & Sons, Inc.; 2003. pp. 6.5.1–6.5.14. [DOI] [PubMed] [Google Scholar]
  • 8.Frati F., Simon C., Sullivan J., Swofford D.L. Gene evolution and phylogeny of the mitochondrial cytochrome oxidase gene in Collembola. J. Mol. Evol. 1997;44:145–158. doi: 10.1007/pl00006131. [DOI] [PubMed] [Google Scholar]
  • 9.Huelsenbeck J.P., Crandall K.A. Phylogeny estimation and hypothesis testing using maximum likelihood. Annu. Rev. Ecol. Syst. 1997;28:437–466. [Google Scholar]
  • 10.Akaike H. A new look at the statistical model identification. IEEE Trans. Aut. Control. 1974;19:716–723. [Google Scholar]
  • 11.Akaike H. Information theory and an extension of the maximum likelihood principle. In: Petrov B.N., Csaki F., editors. Second International Symposium on Information Theory. Budapest: Akademiai Kiado; 1973. pp. 267–281. [Google Scholar]
  • 12.Sakamoto Y., Ishiguro M., Kitagawa G. NY: Springer; 1986. Akaike Information Criterion Statistics; p. 320. [Google Scholar]
  • 13.Sugiura N. Further analysis of the data by Akaike's information criterion and the finite corrections. Comm. Statist. Theor. Meth. 1978;A7:13–26. [Google Scholar]
  • 14.Hurvich C.M., Tsai C.-L. Regression and time series model selection in small samples. Biometrika. 1989;76:297–307. [Google Scholar]
  • 15.Schwarz G. Estimating the dimension of a model. Ann. Stat. 1978;6:461–464. [Google Scholar]
  • 16.Kass R.E., Wasserman L. A reference Bayesian test for nested hypotheses and its relationship to the Schwarz criterion. J. Amer. Stat. Assoc. 1995;90:928–934. [Google Scholar]
  • 17.Raftery A.E. Bayes Factors and BIC: comment on ‘A critique of the Bayesian information criterion for model selection’. Sociol. Met. Res. 1999;27:411–427. [Google Scholar]
  • 18.Weakliem D.L. A critique of the bayesian information criterion for model selection. Sociol. Met. Res. 1999;27:359–397. [Google Scholar]
  • 19.Forster M.R., Sober E. Why likelihood? In: Taper M., Lele S., editors. The Nature of Scientific Evidence: Statistical, Philosophical, and Empirical Considerations. Chicago: University of Chicago Press; 2004. pp. 153–190. [Google Scholar]
  • 20.Burnham K.P., Anderson D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach. NY: Springer-Verlag; 2003. p. 488. [Google Scholar]
  • 21.Abascal F., Zardoya R., Posada D. ProtTest: selection of best-fit models of protein evolution. Bioinformatics. 2005;21:2104–2105. doi: 10.1093/bioinformatics/bti263. [DOI] [PubMed] [Google Scholar]
  • 22.Maddison D.R., Swofford D.L., Maddison W.P. NEXUS: an extensible file format for systematic information. Syst. Biol. 1997;46:590–621. doi: 10.1093/sysbio/46.4.590. [DOI] [PubMed] [Google Scholar]
  • 23.Kingman J.F.C. The coalescent. Stochastic Process Appl. 1982;13:235–248. [Google Scholar]
  • 24.Hasegawa M., Kishino K., Yano T. Dating the human-ape splitting by a molecular clock of mitochondrial DNA. J. Mol. Evol. 1985;22:160–174. doi: 10.1007/BF02101694. [DOI] [PubMed] [Google Scholar]
  • 25.Yang Z. Among-site rate variation and its impact on phylogenetic analysis. Trends Ecol. Evol. 1996;11:367–372. doi: 10.1016/0169-5347(96)10041-0. [DOI] [PubMed] [Google Scholar]

Articles from Nucleic Acids Research are provided here courtesy of Oxford University Press

RESOURCES