oGNM: online computation of structural dynamics using the Gaussian Network Model

Abstract

An assessment of the equilibrium dynamics of biomolecular systems, and in particular their most cooperative fluctuations accessible under native state conditions, is a first step towards understanding molecular mechanisms relevant to biological function. We present a web-based system, oGNM that enables users to calculate online the shape and dispersion of normal modes of motion for proteins, oligonucleotides and their complexes, or associated biological units, using the Gaussian Network Model (GNM). Computations with the new engine are 5–6 orders of magnitude faster than those using conventional normal mode analyses. Two cases studies illustrate the utility of oGNM. The first shows that the thermal fluctuations predicted for 1250 non-homologous proteins correlate well with X-ray crystallographic data over a broad range [7.3–15 Å] of inter-residue interaction cutoff distances and the correlations improve with increasing observation temperatures. The second study, focused on 64 oligonucleotides and oligonucleotide–protein complexes, shows that good agreement with experiments is achieved by representing each nucleotide by three GNM nodes (as opposed to one-node-per-residue in proteins) along with uniform interaction ranges for all components of the complexes. These results open the way to a rapid assessment of the dynamics of DNA/RNA-containing complexes. The server can be accessed at http://ignm.ccbb.pitt.edu/GNM_Online_Calculation.htm.

INTRODUCTION

An emerging view in structural and molecular biology is that the conformational mechanisms involved in biomolecular functions are determined by the intrinsic dynamics of biomolecules, and the intrinsic dynamics are, in turn, defined by the overall structural architecture (1). A better understanding of structural dynamics that underlie important biological functions has been gained in recent years by modeling biomolecular systems as biomachines. Elastic network (EN) models and simplified normal mode analyses (NMA), have proven particularly useful to this aim, as recently reviewed (2,3). Recently, we have constructed a database (DB) of protein motions, iGNM (4), by using such an EN model, the Gaussian Network Model (GNM) (5,6). The dynamics of 20 058 structures that were accessible in the Protein Data Bank (PDB) (7) in the fall of 2003 have been collected in the iGNM DB. The present study builds on this work to introduce an on-line calculation server, oGNM, for examining the essential dynamics of the complete set of over 34 000 PDB structures, as well as that of user-modified and unreleased structures or models.

Results from the NMAs of proteins can currently be obtained from a number of online sources. The most detailed NMA is performed at the atomic level by the Molecular Vibrations Evaluation Server (MoViES; http://ang.cz3.nus.edu.sg/cgi-bin/prog/norm.pl (8). MoViES calculates the normal modes and thermal vibrations for relatively small structures (<4000 heavy atoms), sending the results via email after seven days. The database of macromolecular movements (MolMovDB; http://molmovdb.org/) features a web submission interface for calculating the five lowest frequency modes (9). WEBnm@ (http://www.bioinfo.no/tools/normalmodes) (10) calculates the slowest fourteen modes and associated deformation energies. Both systems employ the same Molecular Modeling Toolkit (MMTK) package (11) that adopts a residue-level EN representation. Although both provide the option of generating and downloading movies of these modes, they are restricted to the analysis of single domain or single chain proteins, respectively. Online calculations for larger structures can be accomplished by elNémo (http://igs-server.cnrs-mrs.fr/elnemo/index.html) (12). elNémo uses an alternative engine based upon the Rotation Translation Block (RTB) method (13) which collapses consecutive residues into rigid blocks, each representing the nodes in a low resolution EN model. This server requires minutes, hours or longer to calculate the 100 slowest modes for large structures. Our oGNM server provides online calculation of normal modes at the residue-level within a few minutes regardless of biomolecular size.

While a large number of studies have tested and verified the applicability of EN models to proteins, the optimal model and parameters for representing nucleotides remains to be established (14). Two major issues in the application of EN models to biomolecules are the choice of the particular atoms for defining the nodes, and the cutoff distance (r_c) of interactions that define the connectors/springs between the nodes, which are carefully considered in building oGNM. In an initial application of the GNM that accurately described the change in the fluctuation behavior of tRNAs nucleotides between the free- and synthetase-bound-forms (15), a single-node-per-nucleotide, at the phosphorous atom, was used to model free tRNA, while two-nodes per nucleotide, identified by the atoms P and O4′, were used for tRNA complexed with synthetase. Because the distance between the P-atoms of base pair forming nucleotides on adjacent strands varies from 13 to 16 Å, a larger cutoff value, r_p, was adopted compared to that (r_c = 7 Å) commonly used for amino acid nodes (C^α-atoms). Coarse-graining of nucleotides were found to adequately uncover the global motions for translation (16,17) and replication machineries (18). The latter study adopted a three-node-per-nucleotide model, using the P-, C2- (base) and C4′- (sugar) atoms with the cutoff distances, r_p and r_c, set to the same value. Given that the average mass of a nucleotide is approximately three times that of an amino acid, such a model may reflect a more consistent EN representation for the entire network.

The oGNM server offers three major advantages: (i) it is not limited to relatively small structures, or single domains; (ii) it returns the results within seconds, i.e. its computational speed is significantly faster compared to existing servers that may require minutes, hours or days to obtain the normal modes; and (iii) it offers a plausible means of elucidating the collective dynamics of oligonucleotides, or DNA/RNA containing structures, in addition to proteins, upon suitable selection of EN model nodes and interaction cutoff distances.

A major utility of such an efficient computational engine is the possibility of interactively assessing the dynamics of sets of structures, and notably extracting dynamic features that typify particular structural or functional families. Recent applications include the comparison of the motions of fold families such as motor proteins (19), globins (20) and polymerases (21), the identification of the highly conserved catalytic triads in proteases (22), or the elucidation of the correlation between catalytic sites and key mechanical sites in a series of enzymes (23). Such analyses suggest that the slow modes provide information on regions and directions of evolutionary changes (24) and functional motions (2,3,25). Clearly there is a great deal of dynamical information/patterns encoded in biomolecular structures that can be efficiently extracted using the oGNM.

MATERIALS AND METHODS

The Gaussian Network Model (GNM)

The biomolecular structure is modeled as a network of N nodes identified by the α-carbon atoms of proteins and other selected atoms of nucleotides (see below). Drawing on the statistical mechanical theory of polymer networks (26), the fluctuations of each node are assumed to be isotropic and Gaussian. The topology of the network is recorded in a N × N Kirchhoff matrix, Γ, where the off-diagonal elements are −1 if the nodes are within a cutoff distance, r_c, and zero otherwise (5,6). The diagonal elements represent the coordination number of each residue. Assigning a uniform spring constant, γ, to all contacts, the cross-correlations between the fluctuations ΔR_i and ΔR_j of residues i and j are evaluated as

$$〈\Delta R_i\cdot \Delta R_j〉=\left(3k_{B}T/\gamma \right){\left[{\Gamma }^{-1}\right]}_{ij}$$ 1

where k_B is the Boltzmann constant, T is the absolute temperature and [Γ⁻¹]_ij is the ij^th element of the inverse of Γ (5,6). Setting j = i in Equation 1, we obtain the mean-square (ms) fluctuations of residue i, 〈(ΔR_i)²〉, which may be directly compared to the corresponding X-ray crystallographic B-factor B_i = (8π²/3) 〈(ΔR_i)²〉 reported in the PDB, thus providing a quantitative measure of correlation between computations and experimental data. GNM yields the distribution of residue fluctuations; the absolute sizes are found by normalizing the results with respect to experimental B-factors (B_i^exp), which permits us to determine γ for a given choice of r_c.

The equilibrium dynamics of the structure results from the superposition of N − 1 nonzero modes found by the eigenvalue decomposition of Γ. The elements of the kth eigenvector, u_k, describe the displacements of the residues along the kth mode coordinate, and the kth eigenvalue, λ_k, scales with the frequency of the kth mode, where 1 ≤ k ≤ N − 1. The contribution of the kth mode to the ms fluctuations of residue i is

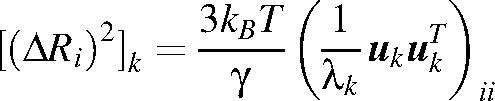2

where (u_ku_k^T)_ii designates the ith diagonal element of the matrix enclosed in parenthesis.

Improved calculation engines

The original implementation of GNM utilized the singular value decomposition (SVD) routine for the complete eigenvalue decomposition of Γ. Although sufficiently accurate and robust for small proteins, this algorithm becomes prohibitive for very large structures because its computational time scales with N³. Rather than calculating the full eigenvalue spectrum, we employ the blocked Lanczos algorithm as implemented in the BLZPACK software (Marques, 1995) to extract only the low frequency modes in oGNM.

For a rapid evaluation of $B_i^{\mathit{GNM}}$, instead of eigenvalues-decomposing Γ into all modes and then adding up all the non-trivial eigenmodes, we introduce a small perturbation of the order of 10⁻⁴ in one element of Γ, which permits us to readily invert the matrix. We then subtract the zero mode from this inverse to obtain the correlation matrix (C), which is verified to be almost identical to the one derived from the conventional SVD approach. $B_i^{\mathit{GNM}}$ is obtained from the diagonal elements of C. Fast extraction of the dominant mode is ensured in this perturbation technique via the Power method, hence the term PowerB for referring to this algorithm (for details see Supplementary Data). Incorporating both BLZPACK and PowerB ensures a dramatic decrease in computing time compared to SVD (see Results).

Selection of a non-homologous set of protein structures

A representative set of non-homologous proteins was retrieved from the PDB-REPRDB (27) for identifying optimal parameters. To this aim, we eliminated membrane proteins, and small proteins (N < 40); we retained structures having no chain discontinuities (gaps) and resolved by X-ray crystallography with a resolution ≤2.4 Å and R-factor ≤0.3. We grouped the resulting set of PDB structures into families, such that members within each family would have sequence identity ≤30% and structural C^α RMSD ≥ 10 Å with respect to members in other families. We further removed proteins where individual chains reside in different chain families, and discarded the structures containing more than 5 nt, those that did not report temperature factors (B^exp), or led to the ‘eigenvalue error’ due to incomplete or inaccurate atomic coordinates (4), or contained C^α-atoms that were assigned multiple positions as solved by X-ray crystallography. This resulted in 1250 families, the PDB identifiers of which are listed in Table 1, Supplementary Data.

Selection of nucleotide-containing structures to test competing models

We extracted a representative set of 64 structures from the 2742 structures available in the nucleic acid database (NDB) (28). Each structure contained at least 70 RNA nucleotides and had experimental B-factors reported for all heavy atoms. Additionally, the number of ribosomal RNA complexes was limited to the four 30S rRNA and seven 50S rRNA structures with the highest resolution. Three models and a broad range of r_p values were considered to assess the model and parameters that best reproduce experimental fluctuation spectra: (i) one-node-per-nucleotide centered on the P-atom (M1), (ii) two-nodes-per-nucleotide at P- and sugar O4′-atoms (M2) and (iii) three-nodes-per-nucleotide at P-, sugar C4′- and base C2-atoms (M3). The cutoff distances for amino acid-nucleotide contacts were set to the average, (r_c+r_p)/2.

RESULTS

Generation of output files

Any file smaller than 10 MB can be submitted in PDB format to the oGNM website to generate output files. The Kirchhoff matrix is constructed by default using the C^α atoms (for amino acids) and P-atoms (for nucleotides) as the network nodes with respective cutoff distances of r_c =10 Å and for r_p =19 Å; and the cutoff distance for C^α-P interactions is fixed at the average of r_c and r_p, although the user is also allowed to change the cutoff distances. The current version of oGNM computes GNM dynamics for structures up to 12 000 nodes. In the case of NMR structures, calculations are performed for the first reported model only; however, the user may manually edit such files and submit any NMR model for calculation.

The output files released by oGNM include (i) the comparison of computed and experimental B-factors displayed as square fluctuation profiles versus residue index as in Figure 1c and color-coded ribbon diagrams, (ii) the shapes of the 20 lowest frequency (u_k, k = 1, 20) modes (i.e. the square displacements of the individual residues induced by mode k), presented as mobility distribution curves and color-coded ribbon diagrams (Figure 1a and b), (iii) the cross-correlations between residue fluctuations (Figure 1d), and (iv) the structural regions/domains subject to anticorrelated motions in selected modes, shown in two-colored (e.g. blue and red) ribbon diagrams. A detailed description of the output files, their formats and significances is provided in previous work (4). The ms fluctuations of residues are obtained using the PowerB method, which also yields the correlation coefficient between B^exp and B^GNM, and the value of the effective spring constant, γ. The cross-correlation map gives the normalized correlation

$$C_{ij}={〈\Delta R_i\cdot \Delta R_j〉/\left[〈{\left(\Delta R_i\right)}^2〉〈{\left(\Delta R_j\right)}^2〉\right]}^{1/2}$$ 3

between the fluctuations of residues i and j. The correlations vary between −1 to 1, and they are presented by color-coded maps as illustrated in Figure 1d. A value of −1 refers to a perfect anti-correlation between residue fluctuations, i.e. the motions of residues i and j are coupled but in opposite directions (colored dark blue), while +1 indicates the perfect concerted motion in the same direction (dark red). C_ij = 0 for uncorrelated (or perpendicular) fluctuations. Currently, cross-correlation maps are reported for submitted structures containing less than 500 nodes.

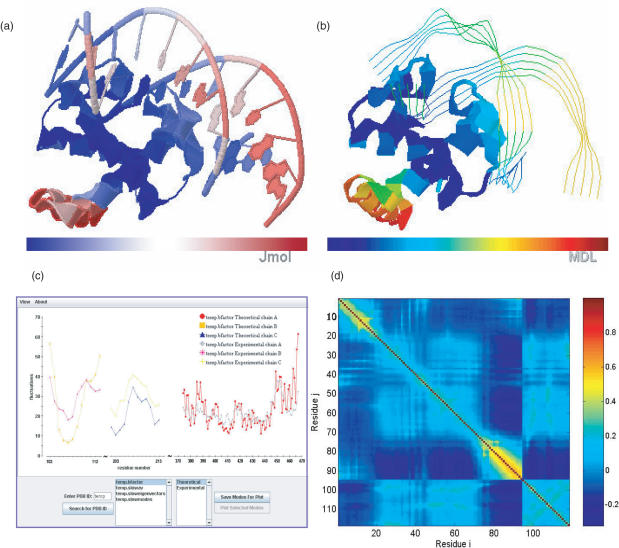
Figure 1.

Visualization of oGNM dynamics results for protein–DNA complex (PDB file: 1j1v). (a) Color-coded ribbon diagram illustrating the mobilities in the lowest frequency GNM mode using Jmol. The structure is colored from blue, white, to red in the order of increasing mobility. (b) Chime representation of the lowest mode for 1J1V; the structure is now colored from blue, green orange, to red. (c) Comparison of experimental and theoretical B_i factors with each chain shown as a different curve. In this example the correlation coefficient between computed and experimental data are 0.642. (d) Cross-correlation map, C_ij, between residue fluctuations, plotted as a function of residue indices i (abscissa) and j (ordinate). The pairs subject to fully correlated motions (C_ij = +1) are colored dark red; those undergoing anti-correlated motions (i.e. C_ij < 0) are colored blue, and moderately correlated and uncorrelated (C_ij ≈ 0) regions are yellow and cyan, respectively. Note that the residue numbers in (d) refer to the index of EN nodes, 1–94 for the protein and 95–118 for the DNA double strands. The mapping of these indices to PDB file residue numbers can be found in the output files delivered by oGNM.

Visualization of results

An interactive 2D Java applet plot viewer is used for visualization of the slow mode shapes and eigenvectors. Users are able to load selected modes and compare them with each other. oGNM supports 3D visualization of modes using Chime plug-in (MDL Information Systems, Inc. www.mdlchime.com), as in iGNM, and Jmol (http://jmol.sourceforge.net/), an open source molecule viewer written in Java. Since Jmol is a cross-platform applet running under the Java Virtual Machine (JVM) 1.1 included in most popular browsers, it is deployed easily without requiring the downloading or installation of additional software. Chime is not available for all the operating systems. However, both engines are built upon the Rasmol scripting language allowing users to manipulate the color-coded structures in similar ways. The default visualization scheme uses a ribbon diagram representation. A comparison of these two 3D visualization engines for the protein/DNA complex, DnaA/DNA (PDB ID: 1j1v) slowest mode is provided in panels Figure 1a and b.

Improved algorithms afford real-time online calculations

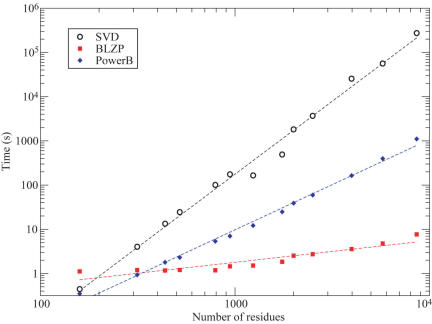
A small set of 13 proteins structures ranging in size from 159 to 8592 residues was used to benchmark the accuracy and efficiency of PowerB and BLZPACK implemented in oGNM for accelerating the computations. Figure 2 shows the computing time versus the number of nodes (N) for both methods as well as the SVD method to calculate all GNM modes and B_i^GNM. The SVD computing times exhibit a power law of the form t ∝ N^3.3. The PowerB method (blue diamonds) yields t ∝ N^2.04, and BLZPACK (red squares), t ∝ N^0.49. The reduction in computing time is especially remarkable in the case of large structures. For example, the SVD calculation for the 5748 residue PDB structure of carbamoyl phosphate synthetase (PDB ID: 1c30), requires 15.6 h, as opposed to only 6.6 minutes using PowerB to obtain the summation of N − 1 modes, and 4.76 s using BLZPACK to extract the slowest 100 modes. In addition, the correlation coefficient between the values of B_i^GNM obtained by PowerB and by SVD methods is unity for all proteins, showing that the PowerB approximation identically reproduces the results found by SVD.

Figure 2.

Relationship between computational time and structure size for different algorithms used in the GNM analysis. The computational times (seconds) are plotted on a log-log scale against the number N of residues for 13 test proteins. The amount of time required to calculate all the GNM modes and theoretical B-factors (B^GNM) by the standard SVD approach (black circles) scales as t_SVD = 2.2 × 10⁻⁸ N^3.30. The PowerB calculation (blue diamonds) scales as t_Power = 7.2 × 10⁻⁶ N^2.04. The computation of the 101 slowest modes using BLZPACK (red squares) exhibits a power law of t_BLZP = 5.9 × 10⁻² N^0.49. Using the latter two methods sequentially results in a dramatic decrease in computing time without loss of accuracy. The improvement is especially significant for large structures (N > 2000), permitting us to release on-line results in oGNM.

Cutoff distance has little effect on GNM dynamics of proteins

A representative protein from each of the 1250 non-homologous families (Supplementary Data, Table 1) was examined to assess the effects of cutoff distance, r_c, and X-ray diffraction temperatures (XDT) on the correlation coefficient, ρ_B, between B_i^GNM and B_i^exp. Supplementary Figure S1 presents results for seven discrete values of r_c and evaluations for subsets grouped into three experimental XDT ranges. At r_c = 7.3 Å, the force/spring constant averaged over all structures is found to be k_BT/γ = 1.10 ± 0.50 Ų in close agreement with the result of k_BT/γ = 0.87 ± 0.46 Ų previously obtained by Phillips and coworkers for a set of 113 monomeric proteins (29). This spring constant provides a measure of a generic ‘stiffness’ that controls residue fluctuations in folded proteins. The results indicate that the B_i^GNM calculations are rather insensitive to r_c over the range 7.3 ≤ r_c ≤ 15 Å. Although the ms fluctuations of residues scale with their inverse coordination numbers to a first approximation, the correlation is significantly improved (>15%) upon considering the contributions due to couplings from all residues, as is done by GNM. Comparing the different XDT subsets shows a trend for improved correlation with experiments in the cases of higher XDTs, indicating that the GNM results agree better with experiments when the structures are subject to less constrained (or larger) fluctuations.

A better EN model for nucleotides

As noted in the introduction section, few existing NMA web servers include a representation for oligonucleotides in their underlying EN model. Although pure oligonucleotide (DNA/RNA) structures and protein–oligonucleotide complexes account for only a small fraction (∼0.5%) of all the structures deposited in the PDB, these structures are involved in some of the most important subcellular functions, such as gene replication, storage and repair, indicating the necessity to properly model the DNA and RNA components' dynamics in EN calculations.

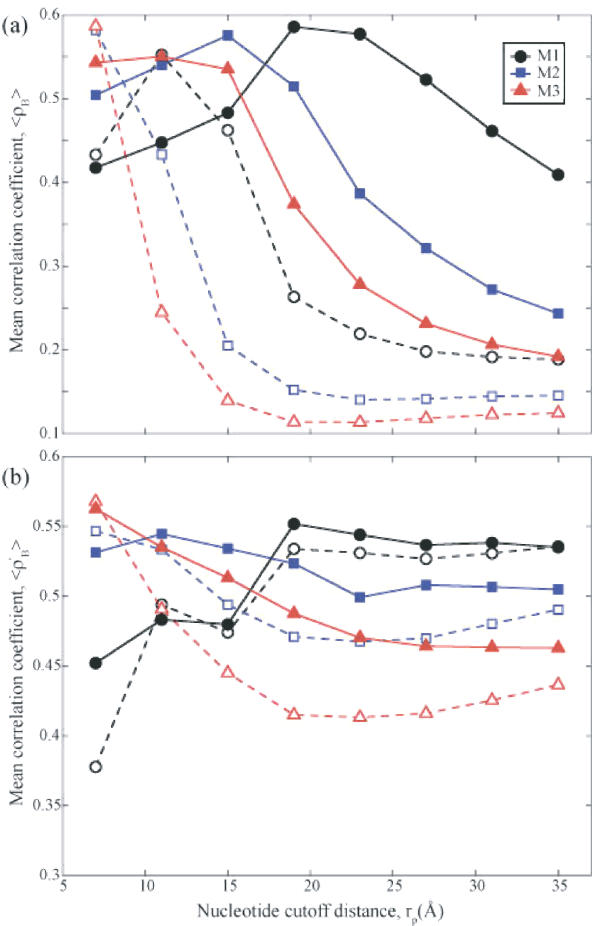
We examined the 〈ρ_B〉 values averaged over a representative set of 64 oligonucleotide/protein–oligonucleotide complexes (Supplementary Data, Table 2) for different models. In general, we expect the predictions for larger structures, or the most collective modes, to be more accurate due to central limit theorem. The slowest modes are, in fact, closely preserved for large structures in coarse-grained representations (25,30,31). The choice of models becomes more consequential in smaller structures. Figure 3a plots the average correlation coefficients 〈ρ_B〉 for all nodes in the examined structures as a function of nucleotide–nucleotide contact cutoff distance, r_p. Results are presented for three models M1, M2 and M3, containing 1-, 2- and 3-nodes per nucleotide, respectively. Two cutoff distances for contacts between amino acids are considered, r_c = 7.3 Å (dashed) and 15.0 Å (solid). For r_c = 7.3 Å, the highest mean correlations occur at a cutoff value of r_p = 7 Å for models M2 (squares) and M3 (triangles), comparable to that (r_c) used for amino acids. For model M1 (circles) the mean correlation peaks around 11 Å, consistent with the necessity to consider longer ranges of interaction when adopting a sparser (P-atoms only) representation of nucleotide so as to account for the interactions between the base paired nucleotides. Calculations reveal that 〈ρ_B〉 rapidly deteriorates for larger values of r_p. One can see that by increasing the value of r_c to 15 Å, (solid curves) the mean correlations shift to higher r_p values in general and remain above 0.50 for a range of r_p. The results for r_c = 15Å indeed reveal the greater robustness of the models obtained upon including more, long-range neighbors; a feature that may be desirable for structures with greater uncertainty (i.e. lower resolution). Sparser distribution of nodes is observed to require a greater cutoff value, again, to best describe the system. Additionally, the fact that the highest 〈ρ_B〉 values for each model are similar, suggests that any of these nucleotide models can produce equally valid results provided that the associated optimal cutoff values are chosen in each case, i.e. (r_c, r_p) ≈ (7, 7), (10, 15) and (15, 19) Å, respectively, for 3-, 2- and 1-node representations.

Figure 3.

Correlation coefficient between experiments and theory for GNMs with different EN nucleotide representations. Results from 3 nt models are shown: M1 (circles) has one-node-per-nucleotide, M2 (squares) has two-nodes-per-nucleotide and M3 (triangles) has three-nodes-per-nucleotide. (a) The average correlation coefficient <ρ_B> of all nodes between B_i^exp and B_i^GNM for a representative set of 64 structures (pure oligonucleotides or oligonucleotide–protein complexes; see Supplementary Table 2) as a function of nucleotide cutoff distance, r_p. In these figures the dashed lines and hollow symbols use r_c = 7.3 Å for the amino acid contact cutoff distance while the solid lines and filled symbols use r_c = 15 Å. For all curves the cutoff distance for contacts between nucleotides and amino acids is (r_p + r_c)/2. For small values of r_p (less than 7 Å) many structures have multiple zero eigenvalues implying multiple disjoint regions of the protein and are thus non-physical models for these structures. (b) The average correlation coefficient 〈ρ′_B〉 between B_i^exp and B_i^GNM for the nucleotide nodes alone, within the same set of 64 structures as a function of r_p. M3 yields the optimal correlations in both cases at r_p = 7 Å, matching the value for the amino acid cutoff distance.

The mean correlation 〈ρ_B′〉 between experimental and theoretical data for the nucleotide nodes only is plotted in Figure 3b for the same two r_c values as above. Here one can gain insight about how well the dynamics of the nucleotide portion of the complexes are predicted. Each set of curves (solid and dashed) demonstrate the same relationship between different models. M1 (circles) is relatively insensitive to r_c values (compare the corresponding dashed and solid curves) but requires r_p ≥19 Å, to achieve best correlation with experiments. All of the models display a more uniform correlation coefficient for large r_p, unlike the decline displayed in panel a. The fact that these values of 〈ρ_B′〉 for r_p ≥ 23Å are higher than those observed in the entire complexes indicates a bias towards modeling the fluctuations of nucleotides to the neglect of protein components. This suggests selecting a smaller value of r_p that is more commensurate with the protein cutoff value (r_c) and thus near the peak of 〈ρ_B〉 in panel a. In fact, the highest 〈ρ_B′〉 value for each of the protein cutoffs studied always occurred for model M3 at r_p = 7Å. However, as in panel a, inspection of the curves suggests ranges for r_c and r_p where each model is optimal.

Since the average mass of a nucleotide is approximately three times that of an amino acid, using the three-nodes-per-nucleotide model (M3) with a universal cutoff of ∼7 Å creates a more consistent EN because each node has the same effective mass. Because the number of interactions per node increases as the cutoff distances increases, the sparseness of the Kirchhoff matrix decreases with increasing cutoff distance. In general sparser matrices are more computationally tractable, supporting the adoption of M3 with r_c = r_p = 7 Å by default. This guideline would be especially useful in systems where the number of nucleotides is similar to or much less than the number of amino acids since it would treat each node equivalently. In systems that are dominated by nucleotides, such as the ribosome structures, it may be preferable to use less nodes and a larger value of r_p to predict the dynamics using less computer memory.

Direct computation of biological units' dynamics

Another important feature of oGNM is the possibility of performing the computations for the ‘biological units’ (32) (http://pqs.ebi.ac.uk) rather than the structures deposited in the PDB about 1/6 of which are different from known biologically active (e.g. multimeric) form. For example, users interested in the dynamics of 1 hho (hemoglobin) can perform the computations for (physiologically active) tetrameric form, instead of the dimer reported in the PDB, by selecting in oGNM the option of performing the analysis for the biological unit. The latter type of computations is visualized using Chime, rather than JMol.

CONCLUSIONS

Since the original proposition of the GNM for estimating protein dynamics (5,6), several studies by many groups led to a deeper understanding of the utility and limits of the applicability of the GNM, and more recently to the construction of a DB of GNM dynamics for known structures, iGNM, (4). The present study builds on this accumulated work to address the following issues: (i) the extension of the methodology to nucleotide-containing structures, (ii) the establishment of guidelines for the use of such models and the parameters necessary for rapid and accurate assessments of these structures, and (iii) the introduction of an efficient on-line server, oGNM, that can routinely update the iGNM DB and allow users to perform computations for query proteins or models not deposited in the PDB.

A major observation here is the possibility of obtaining good correlation with experimental results for nucleotides, or nucleotide-containing complexes, for a wide range of cutoff distances, provided that an appropriate model is adopted for mapping nucleotides into an EN representation. This extends the applicability of the GNM and other EN models to nucleotide-containing structures in general. The use of M3 ensures a representation of the DNA/RNA components of the structures that is commensurate with that of the protein component, as implied by the optimal inter-nucleotide interaction cutoff distance, r_p, that is almost identical to the cutoff distance, r_c, between amino acids.

With the growing number of studies demonstrating the usefulness of the GNM and EN methods, an efficient online calculation engine, such as oGNM is expected to be a useful resource for biologists interested in a rapid assessment of potential mechanisms of action and key residues in their structure of interest, including both proteins, oligonucleotides, or their complexes. Structural coordinates deposited in the PDB often refer to structures crystallized in a multimeric state, or in forms that are not necessarily the biologically functional forms. The iGNM DB reports results only for the structures deposited in the PDB, regardless of their biologically functional forms. Because the web server presented in this paper performs calculations on uploaded structures or biological units of interest, one promising application is to obtain results for complex structures when additional biological information becomes available, thus permitting to investigate the effect of oligomerization or ligand-binding on the dynamics of biomolecular assemblies or complexes.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.