HHrep: de novo protein repeat detection and the origin of TIM barrels

Abstract

HHrep is a web server for the de novo identification of repeats in protein sequences, which is based on the pairwise comparison of profile hidden Markov models (HMMs). Its main strength is its sensitivity, allowing it to detect highly divergent repeat units in protein sequences whose repeats could as yet only be detected from their structures. Examples include sequences with β-propellor fold, ferredoxin-like fold, double psi barrels or (βα)₈ (TIM) barrels. We illustrate this with proteins from four superfamilies of TIM barrels by revealing a clear 4- and 8-fold symmetry, which we detect solely from their sequences. This symmetry might be the trace of an ancient origin through duplication of a βαβα or βα unit. HHrep can be accessed at http://hhrep.tuebingen.mpg.de.

INTRODUCTION

Six out of the ten most populated folds (superfolds) posses an approximate structural symmetry (1,2). Most proteins that adopt one of these folds have no symmetry detectable in their sequences, however, and it is unclear for most domain families in these folds whether their structural symmetry has its cause in an origin through duplication. The ability to detect these structural repeats by their sequences would open a window to study hypotheses about the origin of these domains by duplication of simpler fragments. Furthermore, the detection of structural repeat patterns could help to predict the fold and function of sequences for which no detectable homolog with known structure can be found.

There are three general classes of methods to detect repeats in protein sequenes. Pfam, SMART and REP belong to the first class (3–5). They each use their own database of profile hidden Markov models (HMMs) or sequence profiles that are constructed from known repeat families, and they compare these profiles one by one with the query sequence.

A second class of methods is specialized for the detection of periodic patterns in proteins. They do not allow for gaps within (6) or between repeats (7,8) and are applicable mostly to the large class of fibrous proteins.

Four web servers exist that fall into the third class, that of de novo repeat detection methods: internal repeat finder, REPRO, RADAR and TRUST (9–12). They do not rely on a priori knowledge about repeat families. Instead, they look for internal similarities by comparing the protein sequence to itself with standard sequence–sequence alignment techniques. The main differences among them are (i) how they determine the length and boundaries of the repeat units, (ii) how they adapt the statistics of pairwise sequence comparison to the special case of sequence self-comparison and (iii) whether they utilize transitivity information.

Transitivity has turned out to be an important concept in multiple sequence alignment (where it is called consistency) and has led to significant improvements in this field (13,14). It refers to the fact that if residue i is aligned to j and j to k then residue i must be aligned to k. Owing to transitivity, there is a significant redundancy of information if several pairwise alignments are known. A method that exploits this redundancy will try to find a multiple alignment of all repeats, which is best compatible with all pairwise alignments. Of the aforementioned methods, only TRUST makes explicit use of transitivity, whereas RADAR and REPRO exploit it indirectly during construction of a single-repeat profile from the pairwise alignments.

In developing HHrep, we were guided by the idea to make full use of transitivity and, most importantly, evolutionary information. Homology detection methods have improved enormously in replacing sequence–sequence comparison by sequence–profile and finally by profile–profile comparison. One can expect the same improvements in sensitivity in going from sequence–sequence-based repeat discovery to a profile–profile or even HMM–HMM-based method.

MATERIALS AND METHODS

Like other de novo methods, HHrep is based on self-comparison of the query sequence, but it uses HMM–HMM comparison (15) instead of sequence–sequence comparison. It first builds a multiple alignment from the query sequence by several iterations of PSI-BLAST (16) and constructs a profile HMM from it. It then looks for sub-optimal alignments of the HMM with itself. Optionally, a secondary structure similarity score is included that uses secondary structure states predicted by PSIPRED (17).

The P-value calculation proceeds similar to HHsearch (15): the query HMM is calibrated by searching a small database of representatives from all known SCOP (18) folds. The extracted μ and K parameters of the Gumbel distribution are then used to calculate P-values for the self-comparison, where K is divided by two. The factor two accounts for the reduction in the number of different possible alignments when a sequence is compared to itself, since the score matrix is symmetric.

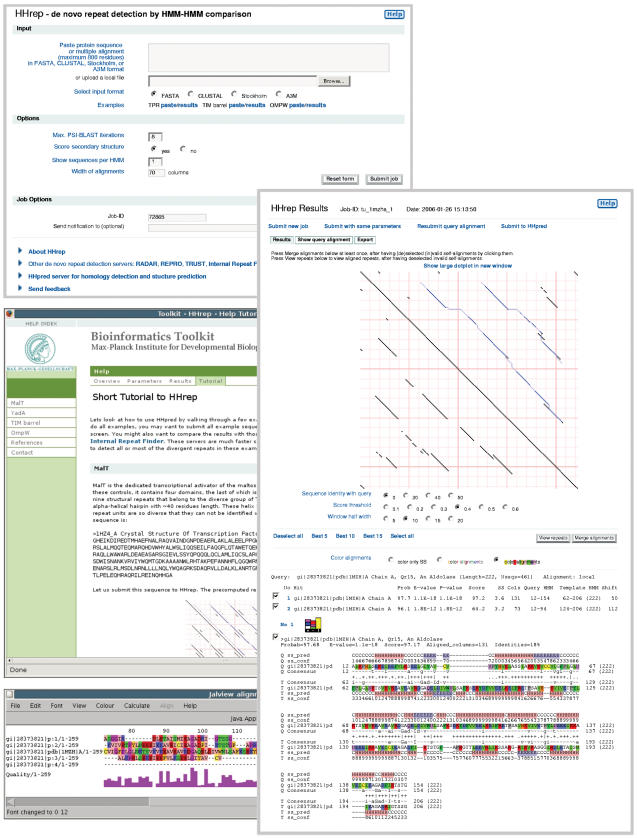
The server returns its results in three sections (See Figure 1, right). On top is a dot plot of the sequence compared to itself, based on profile–profile scores. Cells with a score above a selectable threshold are black, the others white. The main diagonal represents the trivial self-alignment, while the other black diagonal lines indicate regions of local profile similarity. The blue traces in the upper triangular half show the self-alignments found by HMM–HMM comparison. As in the popular dot plotprogram DOTTER (19), scores are averaged over a diagonal window of length 2w + 1 to increase signal-to-noise: The cell (i, j) contains the score ${\sum }_{k=-w}^{+w}{S}_{i+k,j+k}/(2w+1)$, where $S_{i,j}=\text{log}{\sum }_{a=1}^{20}{p}_i\left(a\right)p_j\left(a\right)/f\left(a\right)$ is the profile–profile score between columns i and j, pi(a) are the amino acid frequencies (including pseudocounts) in column i, and f(a) are the amino acid background frequencies (15).

Figure 1.

Start page (upper), sample help page (middle), repeat alignment displayed with JalView (28) (lower), and main results page with a profile–profile dot plot, summary hit list and pairwise self-alignments found by HMM–HMM comparison (right). The self-alignments, which are also shown as blue traces in the upper right half of the dot plot, can be selected and deselected by clicking on them.

The score threshold and the window half-length w can be changed with radio buttons below the dot plot. The top row of radio buttons allows to narrow down the alignment used to build the profile HMM by keeping only those sequences with a minimum sequence identity of 30, 40 or 50% to the query sequence. This is useful when the repeat units have sequence identities among each other of more than 30, 40 or even 50%, respectively. In these cases, adding too distant homologs might smear out the details of the repeat pattern.

The second section below the dot plot consists of a hit list which summarizes the detected self-alignments. HHrep displays the top-scoring self-alignment plus all significant further self-alignments (P-value <10⁻³). In addition to P-values, the list gives the probabilities for each self-alignment to reflect a homologous relationship between the aligned fragments. In contrast to the P-value, this probability includes the secondary structure similarity score (column SS). The last column of the list (‘Shift’) specifies the offset from the main diagonal of the first aligned residue pair.

The last section consists of the pairwise self-alignments. The annotation includes predicted secondary structure, PSIPRED confidence values, the consensus amino acids for the underlying multiple alignment (lower case letters for >40% residue conservation, upper case for >60%) and a central line for the column–column similarity (∣ very high, + high, · neutral, − bad, = very bad). Pressing on the colored histogram logo allows to switch to a histogram view in which colored histogram columns represent the amino acid distributions at each column of the aligned profiles. This view was developed for HHpred (20) and has already proven a powerful tool to quickly spot functional motifs and to discern spurious hits. (More detailed information can be found on the help pages for HHrep.)

Transitivity information is incorporated in a second step by pressing the button ‘Merge alignments’ above the summary hit list. Before, the user should check the detected self-alignments and deselect those that he regards as invalid or unreliable. To understand the effect of the ‘Merge alignments’ button, suppose the query sequence contains four repeats, denoted A, B, C and D, and let us assume that the initial results returned by HHrep contain just one self-alignment, in which A is aligned with B, B with C and C with D. HHrep will then replace the initial alignment ABCD built with PSI-BLAST by a superalignment obtained by merging the two equivalent, pairwise alignments:

$$BCD-ABCD\to ABCD.-ABC$$

When this new alignment is again compared to itself, it will generally show a much cleaner repeat pattern. Often, for instance, previously undetected self-alignments will appear, such as that between ABCD and – – AB.

This alignment-merging step may be performed until the repeat signal does not further improve (once or twice is usually sufficient). Pressing ‘View repeats’ displays the staggered alignment of repeats, constructed by merging all selected self-alignments (Figure 1, bottom). One can also submit the new superalignment to the HHpred server for homology detection and structure prediction (20). Since the merged superalignment is more diverse than the original PSI-BLAST generated alignment, the sensitivity to identify remote homologs may be significantly enhanced.

A limitation of our method is its dependence on sequence homologs. Without a multiple alignment, HHrep is of similar sensitivity as existing methods. This was one of the reasons for us to develop HHsenser (available as web server, see article in this issue). This method often succeeds in finding many more homologs for sequences with few or no BLAST-detectable relatives in the database.

Since HHrep has to build a multiple alignment by iterated PSI-BLAST searches, it is slower than the other de novo methods. But often the user already has a multiple alignment at hand, for example from a previous HHpred search or from secondary structure prediction. In this case, he can use this multiple alignment directly and skip the slow PSI-BLAST step, making HHrep comparable in speed with other de novo servers.

BENCHMARK

To demonstrate the sensitivity/selectivity gain of HHrep over existing methods, we chose to compare HHrep with TRUST, the method that has to date been reported to be most sensitive (12). The benchmark dataset consists of the 50 most populated folds in the SCOP 1.69 database (18), filtered to a maximum sequence identity of 25%. We assigned all folds or superfamilies by hand to three categories, drawing on SCOP annotation about structural symmetries (see Supplementary Data). We obtained 627 repeat-containing sequences, 1750 not containing repeats, and 77 unclassified sequences. The third category was assigned to three folds that contain both duplicated and unduplicated sequences within the same superfamilies.

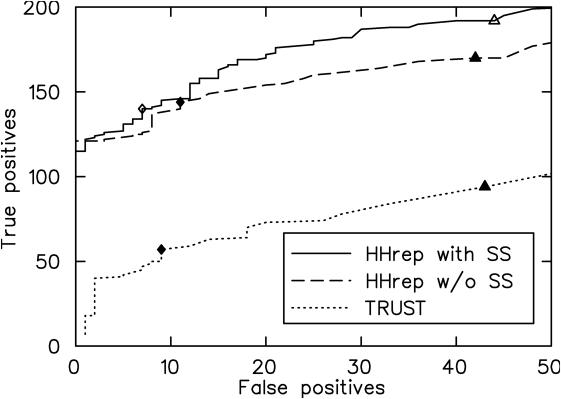
Figure 2 shows a receiver operating characteristic (ROC) plot that compares HHrep with and without secondary structure scoring to the TRUST method. The P-value of the best sub-optimal self-alignment was used for ordering hits. Since TRUST does not print out statistical significance values, we added two lines to the source code for that purpose. The plot shows that HHrep detects between two and three times as many repeat proteins as TRUST over a wide range of false-positive rates.

Figure 2.

ROC plot comparing HHrep with and without secondary structure scoring to the method TRUST (12). Filled diamonds and triangles mark a P-value of 10⁻³ and 10⁻², respectively, the open diamond and triangle indicate a probability of 50% and 10%, respectively.

It should be noted that the constructed benchmark is not particularly hard. It contains a fairly even representation of repeat proteins across all levels of detection difficulty, since we did not remove sequences with high sequence identity between repeats units. The difference between TRUST and HHrep on the difficult cases, for which repeats have significantly diverged in sequence, is therefore expected to be much more pronounced.

The sensitivity of HHrep is difficult to capture in an automated benchmark, since in practice, the user has much more information than just the P-value of the best suboptimal alignment to decide whether a protein sequence contains repeats. The possibility (i) to view the self-similarities in a dot plot representation whose parameters can be interactively optimized, (ii) to accept or reject individual self-alignments, (iii) to inspect a histogram representation of the profile–profile alignments, (iv) to quickly check and correct the query alignment and finally (v) to view the results of the transitivity operation in the dot plot will substantially improve the practical performance of HHrep over the theoretical curve in Figure 2.

ORIGIN OF THE TIM BARREL FOLD

We demonstrate the use of HHrep by studying the evolution of the (βα)₈ or TIM barrel fold, the second most populated fold type among known protein structures (after immunoglobulins). This extremely diverse fold is subdivided into 26 superfamilies in SCOP 1.69 (18) and 18 families in CATH 1.7 (21). However, in recent years evidence has accumulated for a common ancestor of at least half of these superfamilies, based on a comparison of their sequences, structures, as well as positions and similarity of functional sites (21–24). Despite its approximate 8-fold structural symmetry, evidence for an origin of this common ancestor by 8-fold or 4-fold duplication is lacking, due to the inability to detect the repeats on the sequence level. Fani et al. (25) noted an internal 2-fold symmetry in HisA and HisF, two enzymes from the histidine biosynthesis pathway, and proposed an evolutionary scenario in which these proteins evolved by duplication of a common half-barrel ancestor. Based on the newly determined structures of HisA and HisF, Lang et al. (26) later confirmed the 2-fold symmetry and proposed this scenario for all (βα)₈ barrels. Nagano et al. (21) noted a recurrent, partially conserved loop sequence motif (G-X-D) in the superfamily containing HisA and HisF that would indicate a 4-fold symmetry.

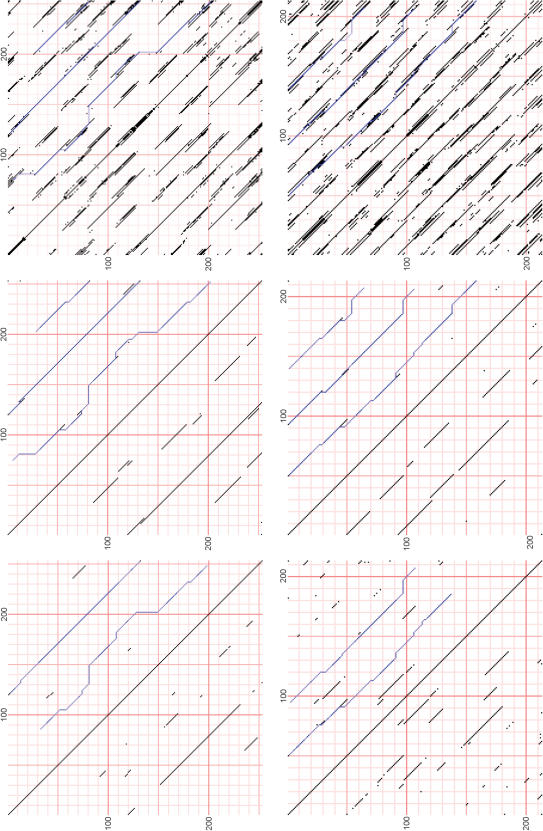
We show here that HHrep can find, within minutes, a distinct 4-, and 8-fold internal symmetry in members from several different SCOP superfamilies of the (βα)₈-fold (Figure 3). First, we indeed find a dominant 2-fold symmetry in HisF (1thf_D, top row) and HisA (1qo2_A, data not shown), with a P-value of 9.7 × 10⁻¹³ for the alignment between the two halves of HisF. But both HisA and HisF also display a weaker but clear 4-fold symmetry with P-value 5.1 × 10⁻⁴ and 5.3 × 10⁻⁴, respectively, for the alignments shifted by one quarter-barrel unit. After two alignment merging operations (Figure 3A, middle) the 4-fold repeat structure is obvious and all three sub-optimal alignments are visible. At lower dot plot threshold (Figure 2, upper right), an 8-fold repeat pattern becomes apparent. KDPG aldolase (1fg0_A) has a distinct 4-fold symmetry (Figure 2, lower left), but here the 2-fold symmetry is not dominant: the alignment of the two halves has a lower P-value (2.5 × 10⁻⁵) than the self-alignment shifted by a quarter-barrel unit (5.4 × 10⁻⁷). Again, at a lower score threshold, an 8-fold symmetry is discernable (lower right). Two further examples with 4-fold symmetry from other SCOP superfamilies are not shown in the figure: phosphoenol pyruvate mutase (1s2w_A) and inosine monophosphate dehydrogenase (IMPDH) (1zfj_A). All sequences were submitted with default parameters.

Figure 3.

The 2-, 4- and 8-fold repeat pattern in TIM barrel sequences. The figure shows profile–profile dot plots of HisF (1thf_D) (upper row) and KDPG aldolase (1fq0_A) (lower row), before (left) and after (middle) incorporation of transitivity information through alignment merging. The dot plots on the right were obtained from the middle ones by lowering the score threshold from the default value (0.4 bits) to 0.1 bits.

Out of the four superfamilies with the most clear-cut examples of internal symmetry, only one superfamily, containing HisA and HisF, has members with a dominant 2-fold duplication. But representative sequences from all four superfamilies possess a distinct 4-fold symmetry and a residual 8-fold symmetry signal. Whereas the strong conservation of the 2-fold symmetry in HisA and HisF can be a consequence of their function—both halves contain a phosphate-binding motif that is required by the nature of their biphosphate substrate—the 4-fold symmetry is not easily explained by functional contraints. We note that the 8-fold symmetry is further underscored by the existence of several sequences with TIM barrel fold that possess 8-fold symmetry with partially conserved GAD motifs (e.g. Thiamine-phosphate pyrophosphorylase, sp∣Q7P1R3∣THIE_CHRVO).

Similarity on the sequence level is generally regarded as indication of common ancestry. Our experience with using HMM–HMM comparison for remote homology detection confirms this common assumption [see, e.g., (27)]. We therefore interpret the symmetry in TIM barrels as evidence for an origin of most, if not all, TIM barrel proteins by 4-fold duplication of a single, ancient quarter-barrel module. One can speculate that this ancient module might itself have arisen by 2-fold duplication of a βα precursor, which would have given rise to the 8-fold symmetry.

The present results support the hypothesis of the origin of protein domains by duplication and recombination of simpler peptides (2). This hypothesis explains how complex domains consisting of hundreds of amino acids and with a combinatorial complexity on the order of 20¹⁰⁰ could have evolved in a finite time, by first evolving shorter peptide modules out of which more complex domains could then have been assembled.

CONCLUSION

HHrep achieves a high sensitivity to detect divergent repeats in proteins by employing a new method for HMM–HMM comparison and making use of the transitivity inherent in the pairwise alignment of repeats. In an automated setting, the sensitivity is increased over current de novo methods by a factor two to three, which can be regarded as a lower limit of the expected improvement in an interactive server setting. We have used HHrep to detect a clear 4-fold repeat pattern in diverse sequences with TIM barrel fold, and at lower score thresholds we find a weak 8-fold symmtery. This supports the hypothesis that TIM barrels originated by 4- and perhaps 8-fold duplication.

SUPPLEMENTARY DATA

Supplementary data are available at NAR Online.