PHEPS: web-based pH-dependent Protein Electrostatics Server

Abstract

PHEPS (pH-dependent Protein Electrostatics Server) is a web service for fast prediction and experiment planning support, as well as for correlation and analysis of experimentally obtained results, reflecting charge-dependent phenomena in globular proteins. Its implementation is based on long-term experience (PHEI package) and the need to explain measured physicochemical characteristics at the level of protein atomic structure. The approach is semi-empirical and based on a mean field scheme for description and evaluation of global and local pH-dependent electrostatic properties: protein proton binding; ionic sites proton population; free energy electrostatic term; ionic groups proton affinities (pK_a,i) and their Coulomb interaction with whole charge multipole; electrostatic potential of whole molecule at fixed pH and pH-dependent local electrostatic potentials at user-defined set of points. The speed of calculation is based on fast determination of distance-dependent pair charge-charge interactions as empirical three exponential function that covers charge–charge, charge–dipole and dipole–dipole contributions. After atomic coordinates input, all standard parameters are used as defaults to facilitate non-experienced users. Special attention was given to interactive addition of non-polypeptide charges, extra ionizable groups with intrinsic pK_as or fixed ions. The output information is given as plain-text, readable by ‘RasMol’, ‘Origin’ and the like. The PHEPS server is accessible at http://pheps.orgchm.bas.bg/home.html.

INTRODUCTION

Electrostatic phenomena are widely manifested as a fundamental feature of protein structure–function relationships (1–5). Protein molecules are very complex dielectric systems but can be treated as ‘solid state’ nanometer particles, immersed in buffered water solutions. Many approaches [‘macroscopic’—continuum dielectrics (6,7) and ‘microscopic’—polarizability (8,10)] were developed with different degree of validity: from simple TK-‘dielectric cavity models’ and analytical solution of Poisson–Boltzmann equation to their non-linear numerical and sophisticated empirical generalized Born solutions (11–13). The application of detailed and complex model description leads to increased difficulties for experimentalists to understand and use such sophisticated models. At present there are number of popular program packages [(14,15) and others] and web servers (16,17) but they are of limited significance for everyday problems of experimentalists. To the best of our knowledge, there is not available web server for fast pH-dependent calculation and analysis of protein electrostatic properties. Such software is needed because proteins are polyelectrolytes and their system of ionizable groups is pH-dependent. Many programs and servers compute pK_as at ‘neutral pH’ yielding pH-independent pK_as, which leads to erroneous results and distorts our view of principal properties of protein molecules, important for their functions. It is known that ‘pK_a’ is directly related to free energy change of the corresponding protolytic reaction (ΔG_a = RTpK_a) and that this ΔG_a is pH-dependent. It is well known that protein pK_as are also pH-dependent, because ionic groups are closely arranged in the molecule. There are excellent theoretical works describing pH-dependent protein electrostatics [(7,18,19) and so on] but they are not straightforward for application by experimentalists. For many years a method addressing aforementioned requirements was developed and applied successfully in Biophysical Chemistry Laboratory at IOCh. The theoretical results are unequivocally validated by comparison with experimental studies as shown in a number of peer-reviewed publications over the years. Typical examples for this are pK_as prediction of lysozyme, BPTI and cytochrome c (21–23); spectrophometric titration prediction and infrared carboxylic groups titration (24), enthalpy of protein ionization prediction (25), pH-dependent protein ultrasonic compressibility analysis (26); local electrostatic potentials (27); electrostatic contribution to a protein crystal lattice energy (28) and so on. The method was also applied to clarify enzyme mechanisms (29) and proved to be an invaluable tool for fast evaluation of electrostatic interactions and their analysis in large biomolecular immunochemical complexes (30). We hope that our server http://pheps.orgchm.bas.bg/home.html will be useful for experimentalist (protein scientist in need for fast evaluation of pH-dependent properties, enzymologists in need of pK values, spectroscopists and the like) as well as for in silico analysis by structural biologists and bioinformaticians. Being fast and easy to use this server is suitable for first acquaintance and training in the field.

METHODS

Protein self-consistent electrostatics

It is generally accepted that a model for protein electrostatics can be build on the assumption of continuum medium description, fixed atom approximation, protein–solvent boundary numerically described by atomic static accessibilities, SA_i [variants of Lee-Richards algorithm (31)] and two type of charges: (i) permanent (pH-independent) partial charges (par) and (ii) proton-binding sites with pH-dependent titratable charges (tit). The model accepts experimentally measured pK_a of model compounds (e.g. N-acetyl amides of each i-th ionogenic amino acids) (pK_mod,i) and evaluates work for charge transfer from highly polar water solvent (ɛ_w = 80) to protein macromolecule (4 < ɛ_p,i < 40). Exposure to the solvent is evaluated by SA_i at absence of other ionic groups. Born term, which is proportional to [1 − (ɛ_p,i/ɛ_w)], is roughly estimated as (1 − SA_i). Partial charges assume values from AMBER and PARSE parameterization sets. Since the ratio of the number of ionic AAR (N_ion) to total number of AAR (N_tot) R_el = N_ion/N_tot is relative high for protein particles with small radii (R_p), the pairwise interaction between any i-th and j-th ionic groups counts contributions from charge–charge, charge–dipole and dipole–dipole interactions which can be simulated by an empirical three exponential curve:

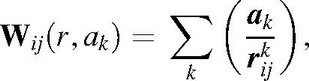where k = 1 for long-range (Columbic) interactions; k = 2 for mid-range, charge–dipole interactions; and k = 3 for short-range dipole–dipole interactions. The a_k were estimated by a non-linear procedure by minimizing the functional F(a₁,a₂,a₃) (21):

$$F\left(a_1,a_2,a_3\right)={{\displaystyle \sum _{{\text{pH}}_i}}\left\{\left[\frac{\partial Z^{\text{exp}}\left({\text{pH}}_i\right)}{\partial \text{pH}}\right]-\left[\frac{\partial Z^{\text{th}}\left({\text{pH}}_i,a_1,a_2,a_3\right)}{\partial \text{pH}}\right]\right\}}^2,$$

where the values of Z^exp are taken from experimental data and Z^th are the calculated values of the protein net charge as a function of pH. The initial values of the coefficients a_k are obtained by numerical approximation of W(r_ij). Through extensive testing, using large dataset of structures, it was found that a₁, a₂ and a₃ values are practically constants for a great number of proteins.

The pH-dependence of the electrostatic potential Φ_el,i (pH) at the i-th proton binding site in PHEI was evaluated according to the following equation:

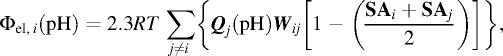where Q_j(pH) is defined by degree of dissociation or statistical mechanical proton population of given H⁺-binding site; Q_j (pH) = (1 − 〈s_j〉) and Q_j (pH) = −〈s_j〉 for basic and acidic groups respectively, where

$$〈s_j〉=\frac{{10}^{\left(\text{pH}-\text{p}{K}_j\right)}}{\left[{1+10}^{\left(\text{pH}-\text{p}{K}_j\right)}\right]}.$$

Thus using partial titration of each j-th group we can find the pH-dependent net-charge of the whole molecule, Z(pH), i.e. potentiometric titration curve:

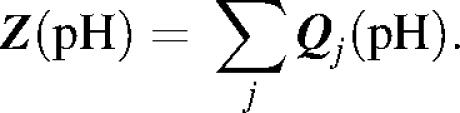By definition if Z = 0 than pH = pI, i.e. the isoelectric point (the only pH at which the dipole moment of a protein molecule can be evaluated).

Thus starting with pK_int,i = pK_mod,i + ΔpK_Born,i + ΔpK_par,i, where pK_mod,i is the pK_a of the i-th site according to model compounds—see set of pK_mod,i in (21,22,29); ΔpK_Born,i is the Born self-energy of the i-th site buried within the ‘uncharged’ protein, and ΔpK_par,i is the contribution of the i-th site interacting with the set of partial (permanent, fixed) atomic charges (see above).

$$\begin{array}{l}\text{p}{K}_{a,i}\left(\text{pH}\right)=\text{p}{K}_{\text{int},i}+\text{p}{K}_{\text{tit},i}\\ =\text{p}{K}_{\text{int},i}+\left(\frac{1}{2.3RT}\right)\\ \times {\displaystyle \sum _{j\ne i}}\left\{Q_j\left(\text{pH}\right)\left(W_{ij}-C\right)[1-(\frac{{\text{SA}}_i+{\text{SA}}_j}{2})]\right\},\end{array}$$

where C is the Debye–Hückel term for ionic strength (Is). The term pK_tit,_i is the pK_a shift of the i-th site caused by interactions with all other proton-binding groups and is evaluated according to efficient self-consistent iterative procedure (32). Coming to self consisted pH-dependent ionization the free energy term G_el(pH) is calculated as follows.

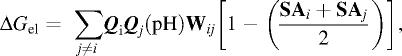as well as pH-dependent Coulomb energy of each i-th ionic group with whole charge multipole:

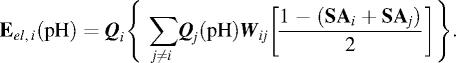After applying this iterative algorithm the electrostatic system is converged and all basic pH-dependent properties are reported.

IMPLEMENTATION

The web sever is a front end of our program package PHEI, developed over many years in our Biophysical Chemistry Lab. Its current version is written in PERL and C/C++ by one of us (A.K.). Our package is capable of much more functionality and only basic electrostatic properties are presented online, the rest being under consideration for the next release (Conclusions and Future). The web implementation is driven by CGI/PERL routines. The only input file is a coordinate file in Protein Data Bank (PDB) format (33)—either user supplied or just as a PDB ID, following retrieval from our local PDB database. Following submission, the user is given some basic information about the protein molecule (chains; number of residues; ratio of ionogenic to all groups, R_el) and warned about certain inconsistencies in structure, related to subsequent calculation (interruption in residue numbering which might influence appearance of terminal charges). The user is given the possibility to edit initial setup of ionogenic groups (attention to CYS in SSBONDs and excluding covalently modified groups). This is accomplished by convenient interactive selection of used set of groups. This gives opportunity for simulation of ‘electrostatic mutagenesis’. Full ‘charge mutant analysis’ is supposed for next versions. The same screen visualizes the PDB file in a text field which allows for direct editing: adding missing terminal charges, fixed (non-titratable) whole or partial charges and titratable groups with user defined pK_a intrinsic. All other parameters used as input are predefined or automatically calculated. After initial setup completion the calculation proceeds through aforementioned steps—evaluation of accessibilities and Born term ΔpK_Born,i, perturbation of pK_a by partial charges ΔpK_par,i and finally the iterative procedure for self-consistent evaluation of titratable ΔpK_tit,i.

To calculate ΔG_el(pH), the following energy conversion units were used: 1 kcal = 4.186 kJ = 1.68RT units (at 298 K) = 0.735 pK_a units. The units of ϕ_i(pH) are kcal/mol·e = 43.176 mV or 30.24 mC/m². All calculations are provided at ionic strength (Is) 0.1.

The obtained results are organized in two groups: (i) GLOBAL [Z(pH), ΔG_el(pH) and Φ_j at fixed pH] and (ii) LOCAL [s_i(pH), pK_a,i(pH), E_el,i(pH) and ϕ_i(pH)]. For each of them there is a link to own page. The contents of each page is comprised of the result itself, related derivatives (e.g. pI, ∂Z/∂pH, pK_1/2 and so on) as well as a short description and examples for visualization of this type of data. All output data files are in standard plain text format. Visualization is straightforward with any 2D plotting software and molecular graphics programs (RasMol, JMol, PyMol and so on).

RESULTS

Global pH-characteristics

(1) pH-dependent protein net charge Z(pH) and its derivatives: Isoelectric point pI/Z = 0 and protein buffer capacity β = ∂pI/∂pH at three pH: (pI − 1.5), pI and (pI + 1.5).

It is equivalent to experimental potentiometric titration curve (34) and reflects basic global electrostatic characteristic of protein proton binding (35). The definition of pI is pH at which Z = 0. Protein buffer capacity (β) is an important parameter for design of precise ion-exchange (36) and electrophoresis (37) experiments. The difference between two Z(pH) of analogous but perturbed states [e.g. apo-holo (30), oxidized-reduced, free-liganded and the like] can be useful in analysis the nature of such perturbation and identify pH region where it has maximal effect on proton binding. Other relevant issues are: the net charge of protein under condition of electro-spray mass-spectrometry (38); the critical Z-values at extreme pH in water (39,40) and in vacuum (41) at which protein ‘denature’ and many others (Supplementary Figure S1).

(2) pH-dependent electrostatic free energy term [ΔG_el(pH)] and its derivatives: ΔG_el,min, ΔG_el,pI; pH_a and pH_b at ΔG_el = 0 for acid and alkaline/basic denaturation, respectively.

Quantitative estimate for charge dependent stability ΔG_el(pH) is basic electrostatic characteristic of protein molecules (2). By evaluating ΔΔG_el,ion(pH) = ΔG_el,holo(pH) − ΔG_el,apo(pH) it is possible to determine pH-dependent specific ion and/or cofactor binding (30). Similarly ‘electron affinity’ can be evaluated from difference ΔΔG_el,e(pH) = ΔG_el,red(pH) − ΔG_el,oxid(pH) (42) and the like. It is easy to obtain experimental values for pH_d,a and pH_d,b and compare with calculated by our server (43). Another option is estimation of stability of pH-induced conformational states and evaluation of energetic barrier between them (44). Presence or absence of stricture ruled charge asymmetry is reflected in ΔG_el,min − ΔG_el,pI difference (also from their pH_min − pI) (Supplementary Figure S2).

(3) Electrostatic potential, EP(Φ_el) at user selected pH for all j-th protein non-hydrogen atoms in a PDB-formatted file and can be visualized in color scale by RasMol.

The electrostatic potential at each point within (45), on the molecular surface (46) and at near vicinity in solvent (47) for a protein molecule is its fundamental electrostatic characteristic (8,48). In fact all above quantities are derivative of Φ_el = f(pH, ligands). Using present PHEPS version output file, it is straightforward to visualize Φ_el (or EP) at each protein non-hydrogen atoms by switching on ‘color by temperature’ using color scale (dark blue: positive EP; green: zeroed EP; and red: negative EP) applicable to entire variety of RasMol model representations (Supplementary Figure S3).

Local pH-characteristics

(4) pH-dependent proton population or degree of ionization of each i-th ionic group (S_i).

The results S_i(pH) for ionic groups in order of increasing sequence numbers are presented in the form of column formatted file (all in one table).

S_i(pH) can be related to NMR pH-dependent chemical shifts, δ_i(pH) (49,50) or other individual titration characteristics—FTIR carboxylate titration (51); differential Tyr UV-titration (52); calorimetric/enthalpy titration [ΔH_i(pH)] (53) and so on (Supplementary Figure S4).

(5) pH-dependent proton affinity pK_a,i(pH) at each individual i-th ionic site: The results pK_a,i(pH) for ionic groups in order of increasing sequence numbers are presented in the form of column formatted file (all in one table). The set of pK_1/2,i for each i-th ionizable group [their pK_as at s_i(pH) = 0.5] is available in another table.

Predicted pK_1/2,i can be compared directly to experimentally obtained. Plotting pK_a,i(pH) is a fast way to differentiate ‘normal’ and ‘abnormal’ titration groups (19,53); functionally important ionogenic sites (54); ΔpK_da = (pK_donor − pK_acceptor) as function of pH to necessary for description pf H+-transfer processes (Hydrogen Bonded Networks, Brønsted's relations and the like) (55,56) (Supplementary Figure S5).

(6) pH-dependent electrostatic energy E_el,i(pH) of interaction of each i-th ionic group with whole multipole of partial and protonic/ionic charges—individual sites and their sum. The results E_el,i(pH) for ionic groups in order of increasing sequence numbers are presented in the form of column formatted file (all in one table).

The pH-dependent Columbic energy of interaction of given ionic group with whole charge multipole is evident characteristic reflecting specific electrostatic site property: influence on charge stability (57), participation in charge-driven processes (58), through space interactions with introduced charged systems in protein complexes (30) and the like (Supplementary Figure S6).

(7) pH-dependent local electrostatic potential, ϕ_i(pH) at each i-th point within protein molecule or its close surrounding. The user is supposed to define points in PDB format. It is recommended that number of points do not exceed 20. The results are presented as pH-dependence of electrostatic potential at each point.

Knowledge of local EP at user-defined points is a great tool for elucidating electrostatic response of these sites to intra/inter-molecular interactions with charged groups (ions and dipoles of different kind of ligands in static and dynamic manner) (59,60). This characteristic is of indispensable use for evaluation of the effect of whole protein electrostatic field on crucially important sites (e.g. for understanding its role in intermediate species of enzyme catalytic cycles (59), protein stability (60,62) and many others (Supplementary Figure S7).

Tested proteins. All these features of our program package PHEI were developed and have been tested for many years. The method was applied to numerous proteins [Supplementary Table 1, (20–30)]. Calculated pK_1/2-s was compared with experimental estimates of pK_as (21,22) and correlation was made of calculated Z(pH) to published experimental curves.

CONCLUSION AND FUTURE DEVELOPMENT

We hope this server will be useful to anyone who needs fast and detailed analysis of pH-dependent properties of a protein with known atomic structure and a tool for protein electrostatic design (61,62). We are ready to share our experience in the field with other protein scientists and are open for discussion.

Features in preparation for next PHEPS version are as follows:

• For each AA in sequence order n (backbone, side chain and residue) with respective (B-factor)_n, static accessibility 〈SA〉_n and φ_el,n.—now implemented.

• 3D-contour EP map generation (in static and dynamic regime)—search of saddle and other critical points on multidimensional maps.

• Correct determination of dipole (at pI) and electric (at any other pH) moments (μ_d and μ_e, respectively) using 3D-EP grid—their scalar and vector values.

• Thorough ‘electrostatic mutation’ analysis with ‘Δ = mut − wild’ as function of pH—data for all mentioned above characteristics: ΔZ, ΔS_i, ΔpK_i, ΔΔG_el, ΔE_el and ΔΦ_el.

• EP gradients (electrostatic forces, EF) at pH control, located at defined atoms and sites (user selected fragments, domains, subunits).

Many of these features are implemented in our program package PHEI, but their online access will be realized after extensive testing.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.