GC-Profile: a web-based tool for visualizing and analyzing the variation of GC content in genomic sequences

Abstract

In order to understand the evolution, structure and function of genomes, it is important to know the general compositional features of DNA sequences. Based on the quadratic divergence, a new segmentation algorithm to partition a given genome or DNA sequence into compositionally distinct domains has been put forward. With the aid of the technique of cumulative GC profile, the distribution of segmentation points can be displayed intuitively. We have therefore developed them into GC-Profile, an interactive web-based software system, which can be used to segment prokaryotic and eukaryotic genomes. GC-Profile provides a quantitative and qualitative view of genome organization. Based on the obtained results, the relationships between the G+C content and other genomic features, such as distributions of genes and CpG islands, can be analyzed in a perceivable manner. It shows that GC-Profile would be an appropriate starting point for analyzing the isochore structure of higher eukaryotic genomes, and an intuitive tool for identifying genomic islands in prokaryotic genomes. GC-Profile is freely available at the website http://tubic.tju.edu.cn/GC-Profile/. In addition, precompiled binaries, together with examples and documentation, can also be freely downloaded for a local execution.

INTRODUCTION

With the advent of high-throughput DNA sequencing, genomic sequences of numerous prokaryotic and eukaryotic organisms have become publicly available. In order to understand the evolution, structure and function of genomes, it is important to know the general compositional features of DNA sequences. Delineating compositionally homogeneous G + C domains in DNA sequences can provide much insight into the understanding of the organization and biological functions of genomes. Furthermore, quantitative analysis of compositional heterogeneity of genome sequences reveals important statistical properties that are useful to locate the origin and terminus of replication in bacterial (1) and archaeal (2) genomes, and to detect horizontally transferred genes and genomic islands (3).

Historically, many windowless methods have been developed to calculate the G + C content, which are usually given the name of ‘segmentation of DNA sequences’. Among them, the methods of entropic segmentation (4,5), hidden Markov model (HMM) (6,7) and wavelet shrinkage technique (8) should be mentioned. Recently, a computer program (IsoFinder), based on a modified version of the entropic compositional segmentation algorithm, has been available online and can be used to identify isochores (9).

Our group has developed a suite of segmentation programs. The first program is the cumulative GC profile (10), which has been applied successfully to prokaryotes (3) and eukaryotes (11). Recently, we also developed a new segmentation algorithm for DNA sequences, which is based on the quadratic divergence (12). We have since developed them into GC-Profile, an interactive web-based software system, available as a public resource at http://tubic.tju.edu.cn/GC-Profile/.

METHODS

A new segmentation algorithm of DNA sequences

The genome order index S is defined by (13)

$$S\equiv S\left(P\right)=a^2+c^2+g^2+t^2,$$ 1

where a, c, g and t denote the occurrence frequencies of A, C, G and T, respectively, in a genome or a DNA sequence, and S can serve as an appropriate divergence measure to quantify the compositional difference between two DNA sequences (12). Consider a genome with N bases. Let n be an integer, 2 ≤ n ≤ N − 1. For a given n, the genome sequence is partitioned into two sub-sequences, one left and the other right. The compositional difference between the right and left sub-sequences can be quantified by the quadratic divergence, as described in the following. Let w₁ = n/N and w₂ = (N − n)/N be two weight coefficients. Let P_l = (a_l,c_l,g_l,t_l) and P_r = (a_r,c_r,g_r,t_r) be two vectors, where a_l, c_l, g_l, t_l and a_r, c_r, g_r, t_r are the occurrence frequencies of bases A, C, G and T in the left and right sub-sequences, respectively. Define the quadratic divergence

$$\Delta S(P_l,P_r)=w_{1}S\left(P_l\right)+w_{2}S\left(P_r\right)-S(w_1{P}_l+w_2{P}_r),$$ 2

where S(P) is defined by Equation 1. The segmentation algorithm proposed here is based on the quadratic divergence. Suppose that n* is a point, at which ΔS(P_l, P_r) reaches maximum, then n* is a compositional segmentation point of the genome found first. The new algorithm is also recursive as in (4,5), i.e. after n* is determined, the same procedure is applied to both the resulting left and right sub-sequences, respectively. Recursively apply the procedure until the halting parameter is less than a given threshold t₀, or the resulting sub-sequence is shorter than a given minimum length (12).

Cumulative GC profile

We define

$$\begin{array}{l}{z}_n=(A_n+T_n)-(C_n+G_n),\\ n=0,1,2,\dots ,N,z_n\in [-N,N],\end{array}$$ 3

where A_n, C_n, G_n and T_n are the cumulative numbers of the bases A, C, G and T, respectively, occurring in the sub-sequence from the first base to the nth base in the DNA sequence inspected. Here z_n is the z-component of the Z-curve, which is a three-dimensional curve that uniquely represents a DNA sequence (14,15). Usually, for an AT-rich (GC-rich) genome, z_n is approximately a monotonously increasing (decreasing) linear function of n. To amplify the deviations of z_n, the curve of z_n ∼ n is fitted by a straight line using the least square technique,

$$z=kn,$$ 4

where (z, n) is the coordinate of a point on the straight line fitted and k is its slope. Instead of using the curve of z_n ∼ n, we will use the z′ curve, or cumulative GC profile, hereafter, where

$$z_n^{\prime }=z_n-kn.$$ 5

Let $\overline{\text{G}+\text{C}}$ denote the average G + C content within a region Δn in a sequence, we find from Equations 3–5

$$\overline{\text{G}+\text{C}}=\frac{1}{2}\left(1-k-\frac{\Delta z_n^{\prime }}{\Delta n}\right)\equiv \frac{1}{2}(1-k-k^{\prime }),$$ 6

where $k^{\prime }=\Delta z_n^{\prime }/\Delta n$ is the average slope of the z′ curve within the region Δn. The above method to calculate the G + C content is called a windowless technique (10).

SERVER IMPLEMENTATION

The web server GC-Profile is implemented on Apache server and the web interface is designed using Common Gateway Interface (CGI) Perl scripts. The segmentation algorithms, which are based on the quadratic divergence and cumulative GC profile, are written in the language of C++. The output graphs are generated by gnuplot graphic routine (http://www.gnuplot.info/).

INPUTS/OUTPUTS OF THE WEB SERVER

Input options

GC-Profile has a user-friendly and intuitive input interface. Users can choose to paste the sequence in the box or upload the sequence (FASTA format) in a file.

The following inputs are required for the web server GC-Profile.

1. Halting parameter t₀ for segmentation. The default value is 1000, but this can be changed according to the requirements of users. Note that t₀ ≥ 0 (12).

2. Minimum length. Generally, the minimum length is set to be 1000 bp for prokaryotic genomes and 3000 bp for eukaryotic genomes (12).

3. Gap size to be filtered. The default value is 1% of the input sequence, i.e. gaps more than 1% of the input sequence are retained, otherwise they are simply deleted. Other values are also provided to satisfy user's need.

4. The graph size to output. It defaults to medium (800 × 600 pixels). User can change the size from small (640 × 480 pixels) to giant (2400 × 1800 pixels).

5. Whether to label the coordinates of segmentation points to the cumulative GC profile.

6. Whether to plot z′ curve instead of −z′ curve. By default −z′ curve is plotted.

7. Whether to set as multiplot mode, in which plots are placed on the same page.

8. Whether to upload a data file containing density distribution of genes (CpG islands; and other genomic elements). With this option the corresponding distribution will be plotted against the G + C content.

9. Whether to upload a data file containing absolute coordinates in the input sequence. This option allows users to label the positions of some interesting genes, e.g. horizontally transferred genes, to the cumulative GC profile. It is very useful to reveal the genomic context of these genes.

Outputs

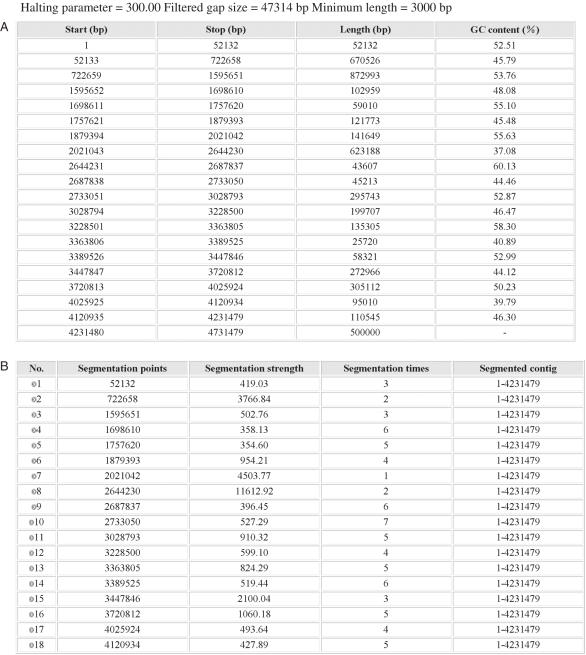
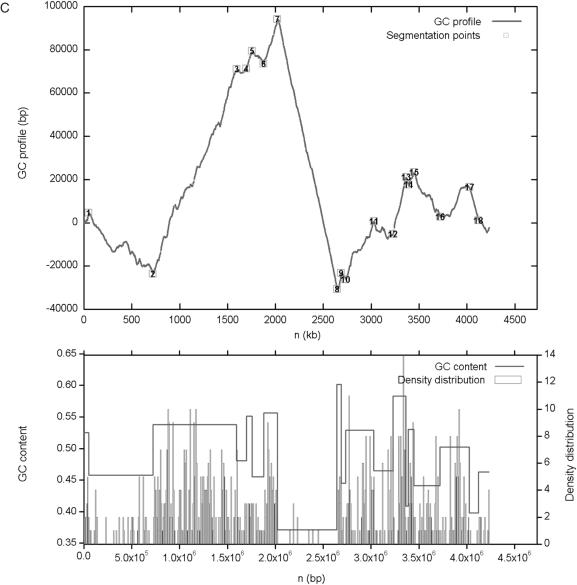
By default GC-Profile generates four files for each job: two tables and two figures. The output web page shows the process of GC-Profile, and provides links to the results of sequence segmentation: (i) coordinates, sizes and G + C contents of the segmented domains as an HTML table (Figure 1A); (ii) number, coordinates, segmentation strength, segmentation times and segmented contig of the segmentation points as an HTML table (Figure 1B); (iii) the cumulative GC profile and (iv) the GC content of the input sequence in PNG format (Figure 1C and Figure 2). If upload options are chosen, the density distribution or the coordinates points labeled to the cumulative GC profile can also be obtained.

Figure 1.

An example of output pages of GC-Profile when the input is the sequence of chicken chromosome 28. (A) Coordinates, sizes and G + C contents of the segmented domains as an HTML table. (B) Number, coordinates, segmentation strength, segmentation times and segmented contig of the segmentation points as an HTML table. (C) The negative cumulative GC profile for chicken chromosome 28 marked with the segmentation points obtained. The lower plot shows the distributions of the G + C content and CpG islands along chicken chromosome 28. The G + C content is calculated for the domains segmented at t₀ = 300. Here, the halting parameter t calculated for each segmentation point is also referred to as the segmentation strength, which is defined based on the quadratic divergence instead of the Jensen–Shannon divergence.

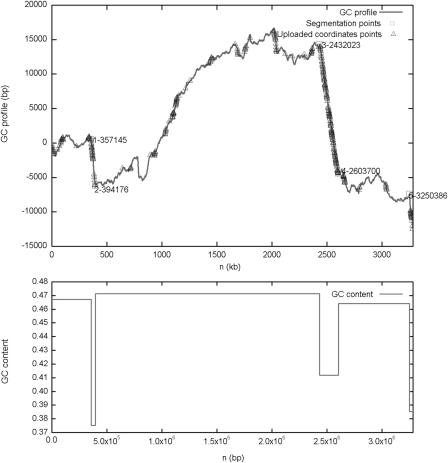
Figure 2.

The negative cumulative GC profile for the genome of V.vulnificus CMCP6 chromosome I marked with the segmentation points obtained. It shows that from 357 145 to 394 176 bp, 2 432 023 to 2 603 700 bp and 3 250 386 to 3 281 945 bp, there are three regions of low GC content, which are recognized as genomic islands. The segmentation points are obtained at t₀ = 100. Here, we also mapped the horizontally transferred genes from HGT-DB to the negative cumulative GC profile. It can be seen that the three regions contain clusters of horizontally transferred genes, which strongly suggests that these regions are horizontally transferred genomic islands.

APPLICATIONS OF GC-PROFILE TO THE ANALYSIS OF DNA SEQUENCES

The potential applications of GC-Profile are presented here and will be utilized to demonstrate how GC-Profile may be used and what kind of information GC-Profile can provide. Each application is demonstrated by a concrete example. Additional examples are accessible from the website http://tubic.tju.edu.cn/GC-Profile/.

Visualization of the isochore organization of eukaryotic genomes

The nuclear genomes of vertebrates are mosaics of isochores, very long stretches (>300 kb) of DNA that are fairly homogeneous in base composition [for reviews, see (16,17)]. The large-scale variation in base composition affects both coding and non-coding sequences and seems to reflect a fundamental level of genome organization (18). This isochore organization shows marked variation in a number of important biological properties, including gene density, chromosome bands, patterns of codon usage, gene length, replication timing, recombination rate and the distribution of transposable elements etc. For more details, see (16,17).

As an example, the isochore map of chicken chromosome 28 is shown (Figure 1). The draft chicken genome sequence, release galGal2, and the associated CpG island data were downloaded from http://genome.ucsc.edu/. To display the global G + C content distribution along the chromosome, gap size to be filtered was set to be 1% of the chromosome size. Applying the segmentation algorithm to the resulting contig, eighteen segmentation points were obtained at t₀ = 300 (Figure 1). The region from 2 021 042 (point 7) to 2 644 230 (point 8) bp was deemed as an isochore. The G + C content of this isochore is 37.08%, the lowest G + C content among the resulting regions. As shown in Figure 1C, this region is a desert region of CpG island distribution, which was calculated in 10 kb long, non-overlapping windows. It is also shown that the obtained segmentation points have clear biological implications. Note that the distribution of CpG islands is closely correlated to the segmented regions with distinct G + C content. It is worthwhile to point out that the segmentation points obtained here are exactly the boundaries of the related regions. For example, there is an abrupt decrease (increase) of the density of CpG islands at the first (second) boundary of the G + C-poorest region between 2 021 042 (point 7) and 2 644 230 (point 8) bp on chicken chromosome 28 (Figure 1C). Similar phenomena are observed in other G + C distinct regions. The cumulative GC profiles and the corresponding isochore coordinates for the latest release of human, mouse, rat and chicken genomes (hg17, mm6, rn3 and galGal2, respectively) at UCSC are also accessible from the website http://tubic.tju.edu.cn/GC-Profile/.

Identification of genomic islands in prokaryotic genomes

Horizontal gene transfer is recognized as a major force for microbial evolution, as it leads to ‘evolution in quantum leaps’ (19,20). Genomic islands are formerly mobile genetic elements that have been acquired by the core genomes via horizontal gene transfer (21,22). They often consist of DNA regions that differ from the core genome in their G + C content and codon usage (22). Depending on the functions they encode, genomic islands can be classified further as pathogenicity islands, metabolic islands, secretion islands, resistance islands and symbiosis islands (21–23).

Below we show the negative cumulative GC profile for the genome of Vibrio vulnificus CMCP6 chromosome I marked with the obtained segmentation points (Figure 2). The segmentation results show that from 357 145 to 394 176 bp, 2 432 023 to 2 603 700 bp and 3 250 386 to 3 281 945 bp, there are three regions of low GC content, which are recognized as genomic islands. These regions have been designed as VVGI-1, VVGI-2 and VVGI-3, respectively in (3). In Figure 2, the negative cumulative GC profile for the genomic islands is distinct from that of the rest of the genome, in that the genomic islands have relatively low GC content, as reflected by abrupt drops in the negative cumulative GC profile at the regions of the genomic islands identified. The abrupt drop in the negative cumulative GC profile indicates that there are clear boundaries between the genomic islands and the surrounding regions. In addition, these three regions have many conserved features of genomic islands. For example, VVGI-1 and VVGI-2 have integrase genes at the 5′ end. VVGI-3 has unusual GC content, codon usage and amino usage, and eight transposase genes. For more details, please refer to (3). Here, we also mapped the genes in horizontal gene transfer database (HGT-DB) (24) to the negative cumulative GC profile. It can be seen that the three regions contain clusters of horizontally transferred genes, which strongly suggests that these regions are horizontally transferred genomic islands.

CONCLUSION

In this article, we present a publicly available, interactive web-based platform, GC-Profile, which is dedicated to analyzing the compositional heterogeneity of DNA sequences. GC-Profile implements a new segmentation algorithm based on the quadratic divergence, and integrates a windowless method for the G + C content computation, known as the cumulative GC profile. The integration of cumulative GC profile with the coordinates of segmentation points leads to a clear graphical representation of the G + C content variation along a genome or chromosome and enables us to establish the relationships between the G + C content and other genomic features, such as distributions of genes and CpG islands. It shows that GC-Profile would be an appropriate starting point for analyzing the isochore structures of higher eukaryotic genomes, and an intuitive tool for identifying genomic islands in prokaryotic genomes. The advantage of the technique is that an investigator is able to study the variation of GC content in a perceivable and precise manner. The precise boundary coordinates obtained by the segmentation algorithm and the associated cumulative GC profile provides a useful platform to analyze a genome or chromosome.