PDB_Hydro: incorporating dipolar solvents with variable density in the Poisson–Boltzmann treatment of macromolecule electrostatics

Abstract

We describe a new way to calculate the electrostatic properties of macromolecules which eliminates the assumption of a constant dielectric value in the solvent region, resulting in a Generalized Poisson–Boltzmann–Langevin equation (GPBLE). We have implemented a web server (http://lorentz.immstr.pasteur.fr/pdb_hydro.php) that both numerically solves this equation and uses the resulting water density profiles to place water molecules at preferred sites of hydration. Surface atoms with high or low hydration preference can be easily displayed using a simple PyMol script, allowing for the tentative prediction of the dimerization interface in homodimeric proteins, or lipid binding regions in membrane proteins. The web site includes options that permit mutations in the sequence as well as reconstruction of missing side chain and/or main chain atoms. These tools are accessible independently from the electrostatics calculation, and can be used for other modeling purposes. We expect this web server to be useful to structural biologists, as the knowledge of solvent density should prove useful to get better fits at low resolution for X-ray diffraction data and to computational biologists, for whom these profiles could improve the calculation of interaction energies in water between ligands and receptors in docking simulations.

INTRODUCTION

Understanding the stability and function of biological macromolecules as well as their interaction with other ligands (effectors, substrates) requires as a prerequisite a quantitative evaluation of their interactions with the solvent. Indeed, being able to predict the solvation energy from just the coordinates of the molecule would be a tremendous advance in drug-design studies and many other issues in computational structural biology.

Current methods that compute solvation fall into two classes: those which represent the solvent explicitly, which are computationally intensive, and those that attempt to model the solvent as a continuous dielectric medium, i.e. implicit solvent models.

In this second class, the Poisson–Boltzmann equation (PBE) is widely used. It is usually solved numerically for solutes of arbitrary shapes using finite difference methods, as pioneered by Warwicker and Watson (1) and later developed by Honig and colleagues and incorporated in their popular Delphi package (2,3). Many programs that solve either the linearized version of PBE, or directly the non-linear PBE, with a variety of scientific computing techniques are now available [see ref. (4) for a recent review].

While it has been demonstrated that these packages give qualitatively correct values of the electric potential in a number of situations (5) (http://honiglab.cpmc.columbia.edu), it is still not entirely satisfying to have to use somewhat arbitrary values for the dielectric constant of the protein (around 2–4), which abruptly jumps to 80 at the interface between the protein and the solvent. This problem still attracts a lot of attention (6).

In this article we describe how a simple solvent description as an assembly of freely orienting dipoles can be readily incorporated into the Poisson–Boltzmann formalism. This is in effect a generalization of the Langevin Dipoles-Protein Dipoles (LDPD) model advocated by Warshel and colleagues (7–9), with the key additional feature that the dipoles are now allowed to have a variable density at each grid point around the solute. Also, it leads to a solvent with a variable dielectric constant that is self-consistently determined by the system.

There is a variety of situations where one would like to have access to the solvent density profile, starting from just the PDB atomic coordinates of the molecule (10). Experimentally, this would lead to better fits with low resolution diffraction data (11,12). Also, better electrostatics calculations would lead to better estimates of intrinsic pKas of buried ionisable groups (13), which are often part of catalytic sites. On the modeling side, this would obviously be useful both to compute solvation energies with much more accuracy than presently (14) and also in understanding the nature of the hydrophobic effect. For instance, in the van der Waals theory of capillarity, the free energy at the liquid–vapor water interface contains a term proportional to the integral of the squared gradient of the solvent density profile and this is currently being used to study the nature of the hydrophobic effect at different length scales (15).

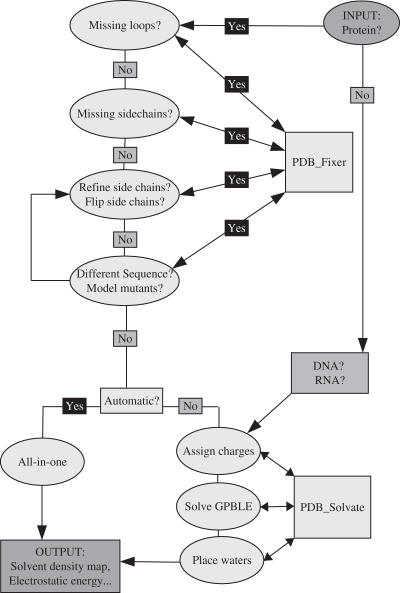
The following section describes the web server and its tools, and a flow chart of the different options is presented in Figure 1. The main focus is put on the new method used to solve for the electrostatics of the macromolecule. The result section briefly describes two applications, one for predicting putative dimerization region(s) on the surface of a globular protein, and the other for predicting regions for lipid binding in membrane proteins. The conclusion section provides a perspective and outlines future work.

Figure 1.

Flow chart of the different options in PDB_hydro.

MATERIALS AND METHODS

PDB fixer

As in other similar servers dealing with macromolecular electrostatics [PDB2PQR—ref. (16) (http://agave.wustl.edu/pdb2pqr), 2004; PCE—ref. (17)], we provide some tools to check the PDB file of interest before submitting it to a PBE solver. Indeed, some PDB files lack atoms, simply because the electron density was not defined for some exposed side chains or disordered loops. If the concerned residues are charged, it may be better to have even a crude estimate of their locations rather than nothing at all. We provide one option that detects missing side chains and builds the rotamer with the lowest van der Waals energy in the context of the (frozen) rest of the protein, for each missing side chain. Another option can detect missing loops, if the numbering of the residues appears to be discontinuous along the chain. The algorithm builds alanines using an idealized conformation of the peptide bond, as described in Hoffmann and Knapp (18). It can deal with interruptions of the main chain up to 21 residues long and then proceeds to generate variants of the conformation of the missing loop by using ‘window moves’. The algorithm was designed to allow for several loops to be built simultaneously. The user can choose the number of different conformations of the loop (typically 10), inspect them visually, and then choose to mutate them by either changing their amino acid type from Alanine to the desired sequence in the PDB file (frozen approximation), or use a more sophisticated algorithm where all the mutated side chains have their conformation optimized simultaneously using the Mean Field Optimization technique described by us earlier (19). This option, called ‘decorate’, can actually be used to do protein design and has been used in the past for such purposes (20). Its input is a PDB file and an alignment file (MSF format) containing the aligned old and new sequences.

The resulting PDB file can be refined to remove bumps coming from the use of rotamers, by minimizing the van der Waals energy of the sidechains using a conjugate gradient minimizer in dihedral angle space, where the needed energy derivatives are calculated according to Abe et al. (21).

Finally, there is an option to refine the network of hydrogen bonds in the PDB file, by allowing 180° flips of the last chi angles of Asn, Gln and His side chains, as amide O and NH2 atoms cannot really be distinguished in experimental electron density maps obtained by crystallographers. The resulting combinatorics can be explored by Monte Carlo (22) restricting the rotamers to the observed and flipped value of the last chi angle for Asn, Gln or His side chains only. However, here it is done with Mean Field Optimization techniques as in (19).

PDB solvate

Once the PDB file contains all side chain atoms, we assign partial charges and atomic radii to each atom of the molecule, according to CHARMM22 (similar to PDB2PQR for APBS); this also works for DNA as well as RNA molecules. For protein–nucleic acid complexes, the user must submit the files separately and then manually merge them. Alternatively, the user can also directly submit the PDB file to the Generalized Poisson-Boltzmann-Langevin equation (GPBLE) solver, with charges generated according to some other Molecular Mechanics package. In the second step, we solve the GPBLE using a multi-grid method (see below), resulting in a 3D map of the electrostatic potential that specifies the free ions density as well as the dipolar solvent density at each grid point. In the third step, this solvent density is used to place water molecules at preferred sites of hydration, according to a threshold that is calculated from the desired level of hydration (usually 0.4 g of bound H2O per g of protein).

To write the analog of PBE in the presence of dipoles p₀ at position r_i we use the fact that the corresponding charge density can be written p₀.grad δ(r − r_i) and then use lattice field theory to enforce self-avoidance of both free ions and dipoles (23). This is similar in spirit to (24), but differs in detail in the way steric clashes are prevented. The partition function Z of the system is evaluated using the saddle-point method (i.e. it is a Mean Field theory), from which all thermodynamic and physical quantities can be retrieved. Details will be given elsewhere (C. Azuara, H. Orland and M. Delarue, manuscript in preparation; (25)).

This results in the final free-energy functional F(Φ) of the form:

$$\begin{array}{l}\beta \mathcal{F}=-\frac{\beta \varepsilon }{8\pi }\int d\overrightarrow{r}{\left|\overrightarrow{\nabla }\Phi \left(\overrightarrow{r}\right)\right|}^2+\beta \int d\overrightarrow{r}{\rho }_{\text{fixed}}\Phi \left(\overrightarrow{r}\right)\\ -\frac{1}{a^3}\int d\overrightarrow{r}\text{ ln }(1+2{\lambda }_{\text{ion}}\text{cosh}\left[\beta ez\Phi \left(\overrightarrow{r}\right)\right]+{\lambda }_{\text{dip}}\frac{\text{sinh}\left[\beta p_{\text{0}}\right|\overrightarrow{\nabla }\Phi \left(\overrightarrow{r}\right)\left|\right]}{\beta p_{\text{0}}\left|\overrightarrow{\nabla }\Phi \right(\overrightarrow{r}\left)\right|})\end{array}$$

where ρ_fixed is the charge density of the solute, a is the size of the dipoles and the free ions, β = 1/k_BT, ɛ is the dielectric constant of the solute, e the charge of the electron, z the valence, p₀ the dipole moment of the solvent and Φ the electric potential; λ_ion and λ_dip are the fugacities of the free ions and dipoles, respectively, which are functions of their concentrations.

This free energy has to be minimized as a function of the electrostatic potential Φ, leading to a GPBLE. In the absence of dipolar species and at low βezΦ, one indeed recovers the linear PBE. The minimization can be performed in a number of ways, such as the relaxation method or the multi-grid method. We implemented both methods, checked that the results agreed, and then settled for the multi-grid method, which is much faster.

IMPLEMENTATION

The web site is organized in two main sections, namely PDB_fixer and PDB_solvate; each section has several options, which each contain a short description, an example, and a form to submit a job. A flow chart of the different steps is presented in Figure 1 and can be accessed from the menu of the web site. Two jobs can be run at the same time and the batch queue status of the server can be displayed at any moment. A number of related links are also provided, as well as a selection of reference articles. Once a job is submitted, the user is directed to a web page that is refreshed every 30 s for 5 min, after which the user is referred to a newly created directory, where the results will be available for 2 weeks. The user may or may not provide his/her email address to be notified of the end of the job.

For all the options of PDB_fixer, the output will consist of one or several PDB files.

For PDB_solvate it will contain several PDB files as well as formatted CNS-style (26) maps that can be visualized with standard molecular graphics programs, such as O (27) or PyMol (28) (http://pymol.sourceforge.net). The typical Solvate protocol involves three steps: assign partial charges (assuming that the PDB file is complete), solve the GPBLE using Multi-grid method and place water molecules according to the obtained solvent density map. All three steps can be performed in a single job called All-in-one. The PDB_solvate output PDB file contains information in the B-factor column that allows the coloring of the molecular surface with PyMol according to the burying of the surface atom upon addition of the water molecules.

The size of the grid is indirectly specified by the two following parameters that must be provided of the user: (i) the number of grid points in the simulation box along each direction, which must be of the form 2ⁿ +1 and (ii) the number of Bjerrum lengths between the border of the grid and the border of the molecule. L_B is the length at which the electrostatic interaction between 2 unit charges becomes comparable to thermal energy kT (l_B = 7 Å at 293 K); usually 2l_B is sufficient. The molecule is centered on the grid prior to any electrostatic calculation.

Other input parameters include the size of the ions (taken as the same as the size of the solvent dipoles), the strength of the dipoles (in Debye), as well as the concentration and valence of the free ions. It is important to realize that the system deals with two types of unrelated grids: one that enforces the finite size effect of the free ions and the dipoles, and one that is used to solve the non-linear GPBLE. In the future, we plan to implement a version of the program that can deal with different sizes for the free ions and the dipoles, or a mixture of dipoles of different concentrations and sizes.

The atomic radii are used to specify the excluded surface of the molecule, which can be of two types: the accessible surface (using the radius of 1.4 Å for the probe sphere) or the molecular surface, calculated on a grid (12) with a probe radius of 1 Å and a shrink radius of 1.1 Å.

RESULTS

For PDB_solvate, we give in Table 1 the CPU times needed for the GPBL solver to converge, for different numbers of grid points and different grid sizes. A comparison is given with the CPU times needed in the same configuration by the APBS software (29). Obviously, the solution of the GPBLE takes longer than the PBE, but it still remains reasonable while generating much more information, such as the solvent density map, the solvent dielectric constant map, the electric field, the angle between the dipole moment and the solute electric field as well as the angle between dipole neighbors.

Table 1.

CPU needed for the GPBLE solver in different grid conditions. Comparison with APBS

Grid size	Nb lB	Grid spacing (Å)		GPBLE		PBE (APBS)
			CPU time (s)	$\Delta G_{\text{sol}}^{\text{elec}}\left(\text{k}T\right)$	CPU time (s)	$\Delta G_{\text{sol}}^{\text{elec}}\left(\text{k}T\right)$
333	1	2.0	34.5	−4581.4	3.5	−3947.3
333	2	2.6	33.5	−5018.4	2.9	−3190.7
333	3	3.0	30.7	−4956.4	2.2	−2813.4
653	1	1.0	295.7	−3579.0	14.8	−3944.3
653	2	1.3	291.2	−3717.9	18.7	−3957.0
653	3	1.5	298.5	−3832.8	17.6	−3940.6
1293	1	0.5	4759.3	−3261.5	94.3	−4030.7
1293	2	0.65	4788.5	−3291.0	84.0	−3994.4
1293	3	0.75	4854.2	−3326.7	102.9	−3974.4

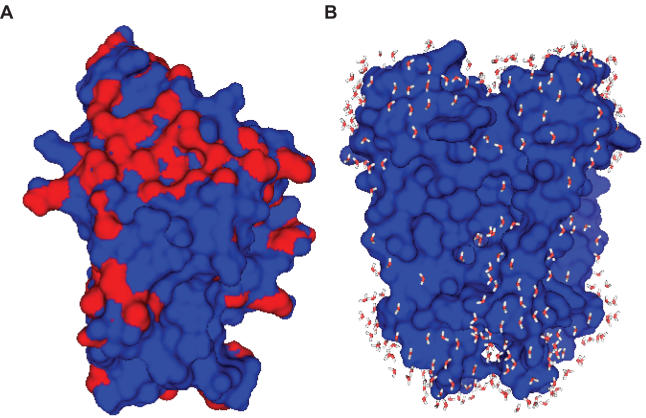
As an illustration of the usefulness of the method, we give two examples where the knowledge of the water density profile clearly correlates with known molecular properties. One is a homodimeric protein (4TMK) whose preferred sites of hydration clearly are excluded from the dimerization zone (Figure 2A). The other is the KcsA membrane protein, where again the lipid binding region is clearly highlighted in the colored surface output by the program and displayed using a simple PyMol script (Figure 2B). We have checked the generality of these results on a number of different homodimeric and membrane proteins, which will be reported elsewhere (C. Azuara, H. Orland and M. Delarue, unpublished data).

Figure 2.

(A) Colored molecular surface of thymidine kinase 4TMK (as a monomer) as a function of surface area buried upon addition of water molecules in the peaks of the solvent density map. The dimerization area appears as the largest poorly solvated (red) patch. Drawn with PyMol (27) (http://pymol.sourceforge.net). (B) KcsA membrane protein: molecular surface and added water molecules at preferred hydration sites. Drawn with PyMol (27) (http://pymol.sourceforge.net). [Supplementary Figure: Radial density profile of the solvent as a function of the surface atom type (see text)].

In addition to the dipole density map, we can calculate the radial solvent density profile, as a function of the nearest surface atom type (C, N or O). The resulting profiles (Supplementary Data) indeed show the expected behavior, with a higher hydration peak for N and O, compared to C atoms.

CONCLUSION AND FUTURE WORK

In the present state of the server, the user can calculate the electrostatic properties of a macromolecule (protein or a nucleic acid) using a new methodology which effectively merges the two existing PBE and LDPD methods. The solvent is accounted for by an assembly of non-overlapping orientable dipoles of variable density. The major advantage of the method is that it generates a solvent density map and a variable dielectic constant map of the solvent. All parameters of the theory are given their physical values. Already, this has proved useful for identifying hydrophobic patches on the surface of proteins.

A number of options and refinements of the method are currently under way; they include: (i) the possibility to have a pH-dependency of the solute charges (30), (ii) the possibility to include the effect of the flexibility of the solute molecule in a dielectric response described by Normal Modes, i.e. a variable dielectric constant inside the solute (31) and (iii) the possibility to include the polarisability of the solvent.

SUPPLEMENTARY DATA

Supplementary data are available at NAR online