Time-resolved optical measurements with spread spectrum excitation

Abstract

We propose a novel method for measuring time-dependent optical quantities. A train of excitation pulses modulated by a pseudorandom bit sequence is used as the light source, and a cross-correlation scheme is used to retrieve the impulse response. Simulation results of the temporal point-spread function of a diffusive wave are provided, as well as experimental results of a fluorescence decay profile. It is demonstrated that our new time-resolved technique can lead to high signal-to-noise ratios and short data acquisition times. A fluorescence-time-dependent suppression process was also been discovered.

Time-resolved techniques are important in optical instrumentation. Measurements of time-dependent transmittance, reflectance, and fluorescence in response to illumination by an impulse of light always contain rich information that can be used to retrieve the dynamics and other properties of the sample under investigation. Time-resolved photon-migration imaging and time-resolved fluorescence spectroscopy and imaging are good examples of such techniques.

Photon-migration imaging has been emerging as a potential clinical diagnostic modality.¹ Conventional time-resolved photon-migration imaging measures temporal point-spread functions (TPSFs), which can be used for quantitative reconstruction of distributions of scattering and absorption coefficients.² Accurate measurement of the rising edge of a TPSF, which is related to that quasi-straightforward propagating component, is desirable for improving spatial resolution.^3,4 Time-resolved fluorescence spectroscopy⁵ and imaging⁶ have been used in a wide range of research areas such as biosciences, chemistry, and clinical diagnosis. The fluorescence lifetime of a chromophore depends on its characteristic internal structure as well as on its physical and chemical environments. Discrimination of signals related to different fluorescence lifetimes has been exploited to suppress background autofluorescence, improve signal-to-noise ratio, achieve high sensitivity and signal specificity, and measure local environmental parameters such as pH, temperature, and ion concentrations. Fluorescence-lifetime imaging microscopy makes it possible to reveal the biomedical processes and reactions within a cell with high spatial resolution. Determination of fluorescence lifetime is generally made in the time domain, in which short excitation pulses are used.

Currently, the temporal profile of the response to an ultrashort light pulse can be measured with either a streak camera or a time-correlated single-photon counting (TCSPC) system. TCSPC is preferred because its dynamic range and temporal linearity are better than those of streak cameras. A few time-resolved systems for medical optical tomography were reported recently, all of which use the TCSPC technique.^7,8 Nonetheless, the principle of single-photon counting requires that no more than one photon be detected in each cycle. This restriction causes a big problem in data acquisition. The maximal count rate is limited by the repetition rate of laser pulses, the processing speed of electronic devices, and the time span of the impulse response. A typical count rate is 100,000 counts per second, which means that approximately 15–30 are required for acquisition of 10⁵–10⁶ photons for one temporal profile. In some applications, multiple detection channels are necessary to keep the overall data-acquisition time under control. For example, Schmidt et al. reported on a 32-channel time-resolved instrument that needs 10–20 min for a complete scan.⁸ It is worthy of mention that far more photon counts are needed for accurate measurement of the intensity of early-arriving photons.

We propose in this Letter a coded excitation and correlation detection mechanism that borrows ideas from spread-spectrum communications. It is well known that a spread spectrum communication system possesses many desirable properties, such as selective addressing capability, low error rate, and interference rejection.⁹ A broadband pseudorandom code has only a weak cross correlation with other codes and an autocorrelation function that is analogous to a delta function. Consequently, a receiving system can pick up the correct code sequence, addressing it from environmental noise and interference, and is able to distinguish the same sequence that arrives at different times from multiple paths. This property is utilized in our time-resolved optical system, in which photons detected at different time delays need to be resolved. Better signal-to-noise ratio, shorter data-acquisition time, and low system cost are the expected advantages of our new technique. Our computer simulations have demonstrated the feasibility of a time-resolved photon-migration imaging system based on spread spectrum excitation. We have also built a primitive time-resolved fluorometer and have conducted a series of experiments with it. The exponential decay profile of a long-lifetime dye was successfully retrieved.

The principle of our method is simple and straightforward. We denote by I(t) the time-dependent response of a sample to the excitation of an ultrashort pulse. A light source continuously modulated with a pseudorandom bit sequence is used to illuminate the sample. So the ac component in the detected signal is proportional to a convolution of the impulse response and the excitation:

$$R(t)=AI(t)*P(t),$$ (1)

where A is the modulation depth and P(t) is an N-bit-long pseudorandom bit sequence. P(t) is a maximal length sequence, which has a circular autocorrelation function similar to a delta function:

$$\begin{array}{l}g(\tau )=\langle p(t)p(t-\tau )\rangle \\ =\{\begin{array}{ll}1\hfill & \tau /T_0=0\hfill \\ -1/N\hfill & \tau /T_0=1,2,\dots ,N/2;,\hfill \\ \hfill & -1,-2,\dots ,\hspace{0.17em}-N/2\hfill \end{array}\end{array}$$ (2)

in which τ is the time delay and T₀ is the bit period. g(τ) increases linearly when τ is within [−T₀, 0] and decreases linearly in [0, T₀]. In regions out of [−T₀, T₀], the autocorrelation values are essentially zero when N is big enough. By correlating R(t) with P(t) we have

$$f(\tau )=\langle R(t)P(t-\tau )\rangle =I(\tau )*g(\tau ).$$ (3)

Equation (3) is valid when the time span of the TPSF is less than NT₀. If T₀ is small enough, f(τ) at a specific delay time τ is well approximated by I(τ). When T₀ becomes comparable to the time scale of I(τ), g(τ) acts as an equivalent temporal gating window. So the impulse response or its integral over a time window can be retrieved by the correlation method.

Time-resolved measurement of diffusive photon density waves by the spread spectrum approach was simulated on a computer. A simulated photon migration imaging system consisted virtually of a four-channel 12.5-Gbit/s pattern generator (MP1775A, Anritsu), a 10-Gbit/s 850-nm vertical-cavity surface-emitting laser transmitter (1780, New Focus), a 12-GHz receiver (1580-A, New Focus), a light-collecting device that effectively increased the detection aperture to 1 mm², and electronic components such as mixers, filters, and amplifiers. A 4095-bit long pseuodrandom bit sequence p(t) (T₀ = 100 ps) generated by the pattern generator was used to directly modulate the transmitter to generate an optical pulse sequence with a 1-mW peak-to-valley value. The optical fibers of the transmitter and the receiver were embedded in an infinite homogeneous turbid medium and were separated by 5 cm. The reduced scattering coefficient of the medium was 6 cm⁻¹, and the absorption coefficient was chosen to be 0.02 cm⁻¹. The ideal response of the receiver to a 1-nJ pulse from the transmitter was denoted V(t) and is proportional to the TPSF that can be computed with the diffusion equation. The receiver’s response to the pseudorandom normal sequence stimulation was given by

$$M(t)=AV(t)*[P(t)+n_s{R}_1(t)]+n_d{R}_2(t),$$ (4)

where A = 10⁻⁴ and where R₁(t) and R₂(t) were random sequences of normal distribution with a unit standard deviation. Noise levels n_s = 0.022 and n_d = 2 mV were derived from specifications of the transmitter and the receiver. The correlation can be performed by a mixer (e.g., ZMX-10G from Mini-Circuit) and a low-pass filter. The reconstructed V(t) is compared in Fig. 1 with the original curve. The noise level in the reconstructed temporal profile was ~6.13 × 10⁻⁵, or 3.2% of the peak value of V(t). Note that fewer than 41 photons could be detected by TCSPC within the same measurement time.

Fig. 1.

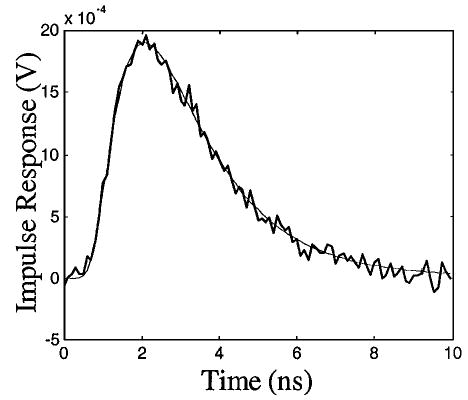
Impulse response representing the TPSF of a diffusive photon density wave. Thin curve, theoretical prediction; thick curve, reconstruction from noisy environments.

To validate our spread spectrum approach experimentally, we built a time-resolved fluoroscopy system and conducted experiments. The experimental system consists of an ultraviolet LED (NSHU550, Nichia America Corporation) whose output spectrum is centered at 375 nm and a photomultiplier tube (R928, Hamamatsu) that is used to detect fluorescent emissions. A personal computer is responsible for generating the same pseudorandom code as mentioned above, synchronizing input and output, and processing digital signals. A train of pseudorandom voltage signals superimposed upon a dc signal is generated from the analog output port of a multifunction data-acquisition card (PCI-MIO-16E-1, National Instruments) and then is power amplified by a current driver to feed the LED. The update rate for the bit sequence is 10⁵ bits/s, and the sequence is generated repeatedly. The coded excitation light is directed to a fluorescent sample through a light guide. The fluorescent photons are converted by the photomultiplier tube into electrical signals, which are amplified by a 40-dB amplifier before being digitized by the data-acquisition card. Digital cross correlation is performed on the computer to retrieve the impulse response, i.e., the temporal fluorescence decay profile. A solution of a kind of europium chelate (Quantum Dye, Research Organics) was used as the fluorescence sample. Quantum Dye has a long lifetime (more than 300 μs), which leads to moderate requirements for system-response speed. The specified excitation wavelength ranges from 360 to 390 nm, and the emission has a peak near 620 nm. An optical long-pass filter was used to separate the emission from the excitation.

An acquired decay profile is plotted in Fig. 2. Initially, the fluorescence intensity decays almost exponentially. However, the intensity crosses zero near ~700 μs and then remains negative for a few milliseconds. The best fit of profile I(t) with two exponential decay terms is given by

Fig. 2.

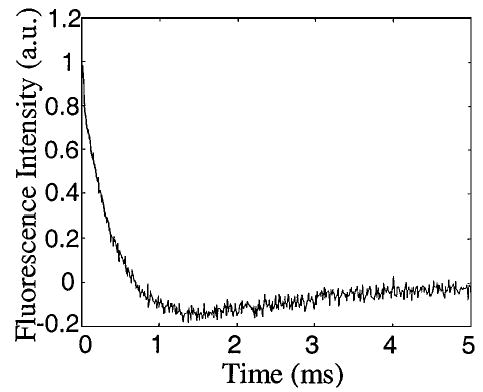
Florescence decay temporal profile of the solution of eropium chelate, Quantum Dye.

$$I(t)=1.33\hspace{0.17em}exp(-t/T_1)-0.389\hspace{0.17em}exp(-t/T_2),$$ (5)

in which T₁ = 424 μs and T₂ = 1745 μs. The second term on the right-hand side of Eq. (5) represents an interesting phenomenon, which we call time-dependent suppression. To the best of our knowledge, this time-dependent suppression process had not been discovered previously. A simple theoretical explanation of it is as follows: An exciting pulse will bring more molecules to higher energy levels and thus temporarily reduce the population of the ground state. Consequently, the excitation rate is suppressed before the system returns to prepulse status. From the additional time constant T₂, one can learn more about radiative and nonradiative transitions involved.

The temporal profile in Fig. 2 was an average over 500 repeated excitations, which took 20.5 s in total. The acquisition time can be reduced to ~4 s if a bit rate of 5 × 10⁵ bit/s is used. The standard deviation of the intensity is essentially independent of time and averages 0.022, ~2.3% of the intensity at the origin of time. Suppose that we measure a fluorescence process described by the first term on the right-hand side of Eq. (5) with an ideal TCSPC system and that the photon-counting rate is set to be 200 counts/s. If the probability that a photon is detected in each circle (5 ms) is 1, the relative statistical error at the origin of time can be estimated by

$$\text{err}=\sqrt{\frac{T_1}{C\mathrm{\Delta }}},$$ (6)

where C is the total number of photon counts and Δ = 10 μs is the temporal resolution. For example, we have err = 2.1% when C = 10⁵. In such a case the total data-acquisition time would be 500 s. Our method can reduce the data-acquisition time by more than tenfold, or significantly improve the signal-to-noise ratio if the same time is spent. Of course, no one will really use single-photon counting for such a slow process. However, the above comparison indicates the great potential of the spread spectrum approach in its future applications in faster optical processes, such as fluorescence decays of nanosecond lifetimes.

To conclude, we have proposed a spread spectrum approach to measuring time-dependent optical processes. Our simulation and experimental results have demonstrated that this new method can remarkably reduce data-acquisition time and (or) improve overall signal-to-noise ratio. In some situations, a much lower system cost can also be expected.