Statistical issues in multisite effectiveness trials: the case of brief strategic family therapy for adolescent drug abuse treatment

Abstract

The statistical development of the multisite Brief Strategic Family Therapy (BSFT) Trial of the National Institute on Drug Abuse’s Clinical Trials Network provides a useful, real example of how an effectiveness trial can differ from an efficacy trial. In particular, two design elements distinguish this effectiveness trial from an efficacy trial. First, because the goal of the trial is to show that the use of BSFT would be an improvement on current practice, it was decided to compare BSFT to treatment as usual at each location. This decision ensures that the trial has the most ecological validity to the participating community treatment providers. Second, the desire to generalize the results to general clinical practice dictates that variability (in effect) across community treatment providers be estimated using a random effects model. These two decisions jointly influence the sample size calculations. Allowing variation in treatment as usual, will increase the variability in effect sizes across sites and estimation of this variability as a random effect necessitates a larger sample size (both number of community treatment providers and participants per community treatment provider), than is the case for a fixed site effect estimate. Details of these effects and their implications for the statistical design are presented.

Introduction

The Brief Strategic Family Therapy (BSFT) Trial is a randomized multisite effectiveness study investigating whether the implementation of BSFT significantly decreases adolescent drug use and problem behaviors relative to current treatment practices within community treatment providers across the United States. This manuscript describes the effectiveness research rationale for the trial, including highlighting differences between efficacy trials and effectiveness trials and how these differences affect the planned statistical test of the hypothesis and associated sample size calculations.

National Institute on Drug Abuse’s Clinical Trials Network

The National Institute on Drug Abuse has established a Clinical Trials Network to facilitate improved drug abuse treatment within the United States by more quickly implementing, in real world community treatment agencies, new treatments that have been shown efficacious in research settings. The implementation of multisite effectiveness trials is the primary mechanism through which the Clinical Trials Network works toward this goal. For a treatment to be sponsored by the Clinical Trials Network, it must have already been shown to be efficacious in at least two efficacy trials. Effectiveness studies proposed within the Clinical Trials Network go through an intensive internal and external review process to ensure that an efficacious research treatment is feasible in clinical practice and that the intervention is indeed likely to be an improvement over current clinical practice. This review also ensures the methodological rigor of the trial. The BSFT trial represents the Clinical Trials Network’s first attempt to transfer complex psychotherapy from research to practice. This study is also somewhat unique in that it is one of the few studies that targets adolescent drug users.

Adolescent drug abuse treatment

Adolescent drug abuse continues to represent one of the most pressing public health issues in the United States. Although trends over the past decade indicate that individual drug use may vary slightly from year to year, US teenagers continue to use illicit drugs at a worrisomely stable rate [1,2]. For example, trends suggest that use of nearly every drug of abuse has remained relatively stable over the past decade, including marijuana, cocaine/crack, amphetamines, heroin, “club drugs”, and others [1]. This trend is paralleled by data indicating the availability of illicit substances. With respect to drug abuse, these trends are also evident in the number of youths mentioned in emergency room treatment for drug related issues [2].

Although population based surveys suggest that adolescent drug use continues at a stable rate, there is strong evidence that specific interventions can have a dramatic impact on adolescent drug use and related behavior problems. Broad reviews of the treatment outcome literature indicate that family interventions in general, and BSFT in particular, are effective with young drug abusers [3–5]. For example, the efficacy of BSFT in reducing adolescent drug abuse and related behavior problems has been shown in multiple studies (for review see [6,7]). Details of the clinical model are provided in the book Breakthroughs in Family Therapy with Behavior Problem Hispanic Youth [8] as well as in a brief treatment manual published by the National Institute on Drug Abuse [9].

Design of the BSFT Trial

The Brief Strategic Family Therapy For Adolescent Drug Abusers Trial (CTN-0014) is an effectiveness study in the Clinical Trials Network. This study randomly assigns 840 drug using adolescents and their families to Brief Strategic Family Therapy (BSFT) or treatment as usual at 14 community treatment sites. Participants will be assessed for drug use at baseline and monthly for 12 months post randomization follow up. Randomization takes place after baseline and just before the initiation of BSFT or treatment as usual.

To enhance generalizability, the study design includes both outpatient and residential treatment modalities. The two treatment modalities are expected to be different in two key ways. First, adolescents from residential settings are expected to be using drugs at a higher rate at baseline than adolescents from outpatient settings. Second, adolescents from residential settings will receive residential services (of varying lengths) between the intake/baseline assessment and randomization. A second baseline measurement of substance use will be administered after completion of standard residential services and immediately prior to randomization of adolescents in the postresidential sample.

This trial has multiple nesting factors and is best conceptualized using a multilevel model. Because BSFT is a family therapy intervention, the adolescent is nested within the family. Because this is a psychotherapeutic intervention in which a single therapist may work with multiple families, adolescents and families are nested within therapists. Finally therapists are nested within treatment sites and treatment sites are nested within modality. Because our primary aim is focused on the outcome of the adolescent, the first level of nesting (the family) does not create analytic challenges. In contrast, the latter levels of nesting – site and modality – are of great importance because the aim of the trial is to establish effectiveness.

The remainder of this manuscript is divided into four sections: presenting some differences between efficacy and effectiveness studies using BSFT as an example; using the primary hypothesis of the BSFT study to illustrate a statistical model that can be used for effectiveness trials; describing the power analysis and sample size calculations for this statistical model; and finally, briefly summarizing the issues presented herein and describing some areas for research to aid in the planning of future effectiveness trials.

Differences between efficacy and effectiveness trials

Level of control

An efficacy trial aims to document the effect of new treatment on participants randomized to that treatment within a tightly controlled environment. An effectiveness trial aims to show that an efficacious treatment can be effective in a broad array of participants and clinical settings [10]. A fundamental difference between effectiveness and efficacy trials is the amount of structure imposed on study design. Efficacy studies are highly structured with homogeneous study populations, standardized (and monitored) treatment, and standardized (and monitored) control condition. In BSFT, the decision was made to maintain full control and supervision of the experimental therapy. In doing so, the rationale was that the first step in establishing effectiveness is to compare the impact of the “purest” form of the efficacious intervention. This decision would be equivalent to implementing a standard dose of medication that had been demonstrated to be optimal in controlled trials. However, unlike many efficacy trials, the therapists that deliver BSFT will be chosen from those working at the community treatment provider. To prevent the possibility of choosing the “best” therapists to deliver BSFT, therapists are randomized to condition (see Inclusion/Exclusion, below). In large part, because of this randomization, the therapists are considered to be research subjects and they must sign informed consent before participating in any aspect of the study. Also, there is no guarantee that a therapist will be able to be trained to criteria in the delivery of BSFT. If a therapist cannot be trained to criteria she or he may be dropped from the study. Therapists who fall below acceptable performance criteria during the trial are required to undertake retraining and may not be permitted to work with new cases if retraining is not successful.

In contrast, conscious decisions were made to have as heterogeneous a population of participants as is available (participant exclusion criteria were minimized) and to allow the control condition at each participating site to consist of the unadulterated usual clinical practice at that site – treatment as usual. Every effort was made in the design of the study to avoid tampering with treatment as usual (e.g., there is no videotaping of treatment as usual).

Inclusion/exclusion

There are three levels of inclusion/exclusion criteria – sites, therapists and adolescents with their families. We have described elsewhere some of the most common challenges involved in transporting BSFT into real world clinical settings [11], including factors related to site characteristics. Here we focus solely on the inclusion/exclusion criteria. Participating sites must be willing to participate and have an adolescent drug abuse treatment facility with adequate participants to ensure at least 30 participants over 12 to 18 months. The treatment as usual in participating agencies must have planned intensity as great or greater than BSFT. To prevent inclusion of treatment too like BSFT in the control group, participating sites’ treatment as usual must not be a manualized family therapy. Nonmanualized family therapy approaches are permitted. In addition sites must be able to identify at least four therapists that meet the therapist inclusion requirements, to facilitate randomization and ensure that results are associated with treatment and not therapist effects. Postresidential sites have two additional requirements (see Treatment modality, below for more description of differences by modality). First, a postresidential site must have some form of postresidential aftercare (to serve as treatment as usual). Second, the agency must work with adolescents from the same geographic area to ensure that therapists will have participating families from a circumscribed catchment area.

Therapists will be randomized to either perform the treatment as usual for that particular site, or be trained and provide BSFT at the site. For this reason, therapists must be qualified to perform treatment as usual at the site, and in many cases will have been performing this treatment prior to involvement with the study. Similarly, because the therapist will be randomized to condition, therapists may not have been previously trained in BSFT. Finally, for the postresidential arm of the study, a therapist cannot have served as a participant’s primary therapist during residential treatment. Each therapist is interviewed and assessed for adequacy of 1) general interpersonal skills; 2) openness to learning new information and responding to feedback; 3) openness to recognizing the role of relationships in influencing behavior; and, 4) directness and clarity of communication. In addition each therapist is required to submit a videotape of therapy with a family. This tape is assessed to determine if the therapist has adequate ability to: 1) convey understanding, acceptance, and respect to all family members; 2) speak with families in a manner that is comfortable and familiar; 3) reflect family members’ comments without being challenging or critical; 4) obtain information from each family member; and, 5) stimulate dialogue between family members. These abilities are assessed using a standardized checklist. Once a pool of at least four therapists are identified at a site that meet these criteria therapists are stratified by academic training and clinical experience and then randomized to condition. Although the selection of the pool of therapists is far from random, randomization to condition ensures that therapists’ abilities are independent of condition assignment.

In contrast to the therapist inclusion/exclusion criteria, the inclusion/exclusion conditions for participants were chosen to maximize the heterogeneity of the potential pool of participants. Participants will be included if they are aged 12 to 17 inclusive and have used any amount of illicit drugs other than alcohol or tobacco in the 30 day period preceding the baseline assessment. Adolescents must currently live with (outpatient) or be expected to live with (residential) formal or informal “family”. Family is defined as any individuals who serve in the legal or traditional role of family members. Adolescents must reside in the same geographical area as the community treatment providers following discharge to permit logistically home based therapy. Adolescents will be excluded if they are to be released to a halfway house, institution, independent or assisted living facility, or temporary foster care because the purpose of this study is to determine the impact of BSFT in a family context. Adolescents with current/pending severe criminal offenses (e.g., murder, attempted murder, aggravated assault, sexual battery/assault) at the time of the initial baseline that may result in short or long term incarceration will be excluded to maximize their availability to the protocol. Finally to be included in the protocol, parents or legal guardians (and a primary caregiver, if different) must sign informed consent and adolescents must assent to be involved in this research protocol.

These inclusion/exclusion criteria should result in a sample with variability in the primary substance of abuse, level of abuse and family factors. These broad and inclusive criteria are consistent with the philosophy of effectiveness trials where the goal is to determine the impact of the experimental intervention on a range of participants that represent “real” community treatment provider patient population.

Experimental (BSFT) condition: standardization and monitoring

The experimental condition, BSFT therapy, will be standardized and monitored with the full rigor of an efficacy trial. Full training to criteria takes approximately six months and involves four three day workshops and weekly supervision of the therapist [9]. Following therapist certification in BSFT, therapists will implement BSFT with study participants. During implementation, therapists will continue to participate in weekly clinical supervision with an experienced BSFT supervisor via group conference calls. This ongoing supervision is an integral component of the therapy model. Whereas some have highlighted a lower level of control of the experimental therapy as a potential characteristic of effectiveness trial [12], supervision of the intervention has been included in all prior efficacy trials of BSFT. Moreover, there is some evidence that ongoing supervision is critically related to successful outcomes in prior effectiveness research with other family based interventions for adolescents with disruptive behavior problems [13] and may be a factor generally with interventions with adolescents [14]. The decision to include ongoing supervision as part of this study is consistent with the philosophy that the first step in determining effectiveness is to test the “purest” version of the intervention in the community. Subsequent research can focus on the sustainability of outcomes with varying levels of supervision.

Control condition: variable treatment as usual

There are some differences in the nomenclature of trials between medication trials and psychotherapy trials. In testing of a pharmacotherapeutic agent, an efficacy trial will frequently involve a placebo control condition. The analogous version of a psychotherapy trial would test the new psychotherapy relative to a time matched attention control [15]. In the case where an established treatment exists, the medication trial would test against the established medication, whereas the psychotherapy trial would test against a time matched effective psychotherapy. In any case, however, the control condition would be well defined and constant across locations if the trial were carried out at multiple locations.

One of the most important discussions in the evolution of this protocol was about what the nature of treatment as usual should be. The team of investigators considered the many benefits of having a standardized treatment as usual condition. For example, a standardized treatment as usual would reduce the number of participants and sites required. However, during deliberations it became clear that a standardized treatment as usual would increase internal validity, but not serve well the mission of the Clinical Trials Network. That is, the goal of improving, through research, the quality of treatment services in the nation. From this perspective, the most important research question that can be asked is “Is BSFT more effective than current practice?” Thus, because a primary aim of this trial is to test the effectiveness (rather than the efficacy) of BSFT in real world treatment settings it was decided to use treatment as usual at each location, as the control condition. Therefore, treatment as usual is expected to show natural variability from site to site. This decision allows for the test of whether implementation of BSFT would be an improvement over the population of treatments that are currently in use for adolescent substance abuse treatment. In contrast, if treatment as usual were standardized, it would be unlike the treatment in most community providers. In that case, were BSFT to be significantly more effective than the standardized treatment as usual, the findings would be of little relevance to participating providers.

It is important to note that this study will permit us to determine effect sizes within sites, thereby providing information about adolescent drug abuse treatment in general, as well as some information to individual programs. The individual programs involved in this trial, for example, will be able to make use of national findings by comparing the effect size for their site with the overall effect size for the national study. Provided BSFT is significantly more effective than treatment as usual across sites, a qualitative comparison of the local effect size to the national effect size may provide guidance to specific community providers. For community treatment providers who are not a part of the trial, the variability in effect size will give them a better picture of the uncertainty around their own potential success if they were to choose to adopt BSFT. Also, because of this variability in treatment as usual, community agencies will be provided with some guidance concerning the size of BSFT’s effect in agencies most like their own.

A second important concern that is ubiquitous in psychotherapy research is to determine whether or not a treatment’s relative efficacy is truly due to the specifics of that treatment, and not solely due to longer duration of treatment. This concern is what has driven the move to time matched alternative treatment in efficacy trials. To address this concern community treatment providers provided a detailed description of their current delivery of services. It was determined that in most cases the number of treatment sessions in treatment as usual services was as great or greater than that planned for BSFT. Thus, it was decided that an eligibility criteria for community treatment providers would include having at least the same intensity of treatment as BSFT.

Handling of site variance

There are three issues concerning the handling of site variance in this multisite randomized effectiveness trial. First, the differences among the sites will be modeled as a random effect to facilitate inference beyond the sites included in the trial. Second, the site by treatment interaction will be included and also estimated as a random effect (interactions of random and fixed effects are typically estimated as random effects). Third, because there are expected differences in the trajectory of drug abuse for adolescents who are treated in a residential setting and those treated in an out-patient program, this modality difference is treated as a stratification factor.

Site as a random effect

The objective of this trial is to ascertain if the use of BSFT for adolescent drug abuse would be an improvement over treatment as usual as practiced by community treatment providers. To address this hypothesis requires that global inference [16] be applied and the results generalized to the population of community treatment providers. This requires that both site and the site by treatment interaction be estimated as random effects. If, either of these terms is estimated as a fixed effect, only local inference is possible, and interpretation of the effects are specific to (or conditional on) the set of community treatment providers in the trial. The estimation of both site and the site by treatment interaction as a random effect allows a generalization of the results to other community treatment providers outside of the trial. It is generally not feasible or desirable to randomly select sites to participate in a trial. However, because we are not randomly sampling community treatment providers we have been careful to document the characteristics of the treatment providers who do participate. This information is important to establish generalizability of the results.

Site by treatment interaction

Estimating the site by treatment interaction as a random effect causes the variance of the treatment effect to increase [16,19] and the associated effect size to decrease. We are using site as a blocking factor. One important implication of this is that (in the balanced case) the denominator of the F statistic for the treatment effect is based on the sums of squares associated with the site by treatment interaction, rather than the error sums of squares as is the case when site is estimated as a fixed effect. This means that the degrees of freedom of the F statistics in the random case is based on the number of sites, rather than the number of participants as in the fixed effect case [17]. Thus, the sample size necessary to achieve a specified level of power is increased [18,19]. A related concern is that there is a minimum number of sites (frequently cited as five) that is necessary to achieve stable estimates of the variability of treatment effects across sites [20]. Even above this minimum number of sites, for some configurations of effect size and variability in effect size across sites and relatively low numbers of sites, increasing the number of participants within the few number of sites will never achieve a desired level of statistical power (i.e., the power curves as a function of number of participants per site for a fixed number of sites may asymptote at values considerably less than 100% power).

There are many site related factors that are potentially related to the level of site variability in the treatment effect. In a multilevel model, one way of increasing power may be to include a site level characteristic, such as mean years of therapist experience in the model. One potential method for increasing power is to include measures predicting this variability in the model. If such variables predict treatment differences at the site level, treatment by site variance would be decreased. This reduction in the size of the (residual) component of variance would lead to an increase in power. The drawback of this approach is that including covariates changes the interpretation of the results to be contingent on a particular value (default being the mean) of the covariates included. In addition, the number of covariates that can be included is limited by the number of sites in the study.

Treatment modality

The BSFT trial includes community treatment providers that provide adolescent drug abuse treatment in one of two modalities – residential services, in which the adolescent is physically living within the community treatment provider’s facility throughout the course of treatment, and outpatient services, in which the adolescent would live with his family, but attend the community treatment provider’s facilities during discrete treatment sessions. In most cases, adolescents selected for residential services are expected to be using drugs at a higher rate at baseline than adolescents from outpatient settings. For adolescents presenting to outpatient therapy, the adolescent will be randomized to BSFT or treatment as usual immediately after completion of baseline assessment; whereas, for adolescents presenting to residential treatment, the assignment to BSFT or treatment as usual would occur after residential services. The treatment as usual in this latter case is the aftercare program of the associated residential service. The baseline assessment for this latter group will occur within approximately two weeks of when the adolescent enters the residential facility. There will be an additional baseline assessment for participants within this modality after completion of residential services and immediately prior to randomization to BSFT or treatment as usual. Stratified randomization procedures will be implemented within site to ensure that adolescents in the two conditions are balanced with respect to ethnicity/race and substance abuse/dependence. There will be full stratification on modality of service in the analysis because each site will be either outpatient or post residential. In addition, because of the anticipated difference in baseline levels of drug use, analyses will estimate the growth curve of drug use, controlling for the individual’s level of baseline drug use – an analysis of covariance type of specification. The timing of follow up assessments for drug use will be monthly in both treatment modalities.

Statistical analysis

Objectives of analysis

The primary goal of this study is to examine the effectiveness of BSFT in the treatment of adolescent drug users. Specifically, it is hypothesized that:

BSFT will be significantly more effective than treatment as usual in reducing adolescent drug use, defined as the percentage of drug use days in 28 day periods.

The outcome variable for this hypothesis is the percentage of days within a 28 day period on which any drug is used. This variable will be constructed from a timeline follow back instrument and will be measured as the sum of the number of days with positive use in 28 day increments (there are 13 28 day periods in 364 days). If there is missing information on the timeline follow back within a 28 day period, the percentage will be calculated as the percentage of available days in that period, as long as not more than 14 days are missing.

The data analysis strategy exploits the nested structure of the data. Thus, in this protocol, assessments are nested within individuals, individuals are nested within community treatment providers, and community treatment providers are nested within modality (outpatient or residential treatment). The statistical model, as defined below, accommodates these different nesting factors. Because in models with many levels of nesting, it is not uncommon for some of the random effects associated with these levels to have close to zero variance, the trajectories will be initially estimated blind to the condition assignment. This will allow an estimate of both the random effects associated with each level of nesting and random effects associated with higher order polynomial trends in time. In addition, this will facilitate the examination and fitting of the residual error correlations overtime. If any of these are statistically not significantly different from zero, they will be dropped from the specification (i.e., set the variance or correlation parameter equal to zero), prior to testing of the hypotheses. For example, if a quadratic term in time is found to have significant variance over individuals, the quadratic term will be included in the hierarchical linear models [18], however, the model as presented below only shows the linear term of the growth model in an effort to keep the notational clutter to a minimum.

The primary hypothesis will be tested using hierarchical linear models [21] to estimate the growth curve of drug use postrandomization. The trajectory of change in drug use will be compared between BSFT and treatment as usual. Hierarchical linear models control for the nesting of both repeated observations within the same adolescent over time, the nesting of adolescents within a community treatment provider (CTP), and the nesting of CTP within treatment modality. These models further allow for a single test of the effect of the intervention across multiple times and sites (see planned post hoc tests, below). Hierarchical linear models permit flexible inclusion of adolescents who may have missed assessments, and allows for nonlinearity of the trajectory of change in the dependent measure. Finally, the hierarchical linear model allows us to consider treatment site as a random effect and to examine variability in treatment effects across sites. The treatment of site as a random effect allows statistical generalization to clinics outside of the study and is consistent with Clinical Trials Network’s mission of testing the general applicability of proven treatments in real world settings. This specification of the test actually compares the effectiveness of BSFT relative to the average effectiveness of treatment as usual in the sites in the protocol. The analysis will include as a covariate the length of residential treatment to control for the amount of residential treatment adolescents receive between the first baseline and randomization. In addition, the amount of change that occurs from the first to second baseline on control covariates will be included as covariates.

In hierarchical linear models the growth curve is conceptualized as separate equations for the intercept and slope, although both are estimated jointly. With the addition of treatment site as a random effect, this model is a three level hierarchical linear model. These three levels are associated with 1) time (within subject), 2) individual (between subjects) and 3) site. To facilitate interpretation of the growth curve, time will be centered on the four month postrandomization assessment (T4). The T4 assessment was chosen because this assessment corresponds to the anticipated termination of services for BSFT participants. Thus, the intercept may be interpreted as the difference between the two conditions immediately postintervention. If the expected ordinal nature of the outcome measure results in sufficient deviation from normality a Poisson link function will be used.

Level 1

The time path of percentage of days having used drugs in 28 day periods will be estimated and the growth trajectory will be parameterized to be a function of BSFT intervention status. Additional predictors will be the stratification variables specified in the urn randomization (ethnicity/race and substance abuse/dependence) and any baseline variables found to predict the occurrence of missing data. The growth curve analysis will include the times after baseline only, and baseline value of the dependent measure will be included as a covariate (i.e., an analysis of covariance parameterization). The presentation below, does not include the baseline value of drug use or these other additional covariates, to ease the exposition. As mentioned this is a three level model. Level 1 describes the trajectory over time for an individual participant:

$$y_{ijt}={\pi }_{ij0}+{\pi }_{ij1}\cdot a_{ijt}+{\varepsilon }_{ijt},$$

where y_ijt, a_ijt, and ɛ_ijt, are percentage of drug use days, time, and a random (or error) term, respectively, for person i, in CTP j, at observation occasion t. The variable a_ijt will be measured as time from assessment point 4 (T4), which occurs approximately four months post randomization. The variables π_ij0 and π_ij1 are the intercept and slope of drug use, respectively for person i, in community treatment provider j.

Level 2

The Level 2 model describes the individual intercept, π_ij0, and the individual slope term π_ij1 as a function of BSFT:

$${\pi }_{ij0}={\beta }_{0j0}+{\beta }_{1j0}BSFT+r_{ij0,}$$

$${\pi }_{ij1}={\beta }_{0j1}+{\beta }_{1j1}BSFT+r_{ij1.}$$

The BSFT variable is a 0–1 or dummy coded variable that is coded 1 if the participant is receiving BSFT, and 0 otherwise. Given this coding of the BSFT variables, β_0j0 and β_0j1 are the intercept and slope, respectively, for participants who are in the treatment as usual condition. The parameters, β_1j0 and β_1j1, are the increments to the intercept and slope of the treatment as usual participants, (β_0j0 and β_0j1, respectively), for participants receiving BSFT at treatment site j (i.e., intercept for BSFT = β_0j0 + β_1j0 and slope for BSFT = β_0j1 + β_1j1). Finally, r_ij0 and r_ij1 are person specific random terms for the intercept and slope.

Level 3

The Level 3 model incorporates the variability across treatment sites into the coefficients of the Level 2 model. Here, a dummy variable is used to allow the variability across treatment status to be a function of postresidential status:

$${\beta }_{0j0}={\gamma }_{000}+{\gamma }_{010}postResidential+u_{0j0},$$

$${\beta }_{1j0}={\gamma }_{100}+{\gamma }_{110}postResidential+u_{1j0},$$

$${\beta }_{0j1}={\gamma }_{001}+{\gamma }_{011}postResidential+u_{0j1},$$

$${\beta }_{1j1}={\gamma }_{101}+{\gamma }_{111}postResidential+u_{1j1}$$

At Level 3, the u terms are site specific error terms In the absence of covariates, γ₀₀₀ is the grand mean of Outpatient treatment as usual at T4 (immediately post intervention), γ₀₀₀ + γ₁₀₀ is the mean of Outpatient BSFT at T4 and γ₁₀₀ is the treatment effect of Outpatient BSFT at T4. Similarly, the mean of Postresidential treatment as usual at T4 is γ₀₀₀ + γ₀₁₀ and the mean of Postresidential BSFT at T4 γ₀₀₀ + γ₁₀₀ + γ₀₁₀ + γ₁₁₀, with the treatment effect of Postresidential BSFT at T4 being γ₁₀₀ + γ₁₁₀ Again, in the absence of covariates, γ₀₀₁ is the rate of change from T4 to T12 for Outpatient treatment as usual, γ₀₀₁ + γ₁₀₁ is the rate of change of Outpatient BSFT from T4 to T12 and γ₁₀₁ is the treatment effect of Outpatient BSFT on the rate of change from T4 to T12. Similarly, the rate of change of Postresidential treatment as usual from T4 to T12 is γ₀₀₁ + γ₀₁₁ and the rate of change from T4 to T12 of postresidential BSFT is γ₀₀₁ + γ₁₀₁ + γ₀₁₁ + γ₁₁₁ with the treatment effect of Postresidential BSFT on the rate of change (relative to Postresidential BSFT) being γ₁₀₁ + γ₁₁₁. Note that γ₁₁₀ is the difference in the effect of BSFT in Postresidential and Outpatient at T4, and γ₁₁₁ is the difference in the rate of change in drug use of BSFT participants in Postresidential and Outpatient modalities In the initial evaluation of this model, should any or all of the Postresidential coefficients, γ₀₁₀, γ₁₁₀, γ₀₁₁, andγ₁₁₁, not be significant, the model will be re-estimated excluding these coeffi cients, greatly simplifying the model.

Whereas the model to be tested is conceptualized in three distinct levels, it is actually estimated as one single equation with multiple fixed and random effects. Substituting in the various equations gives:

$$\begin{array}{l}{y}_{ijt}=[({\gamma }_{000}+{\gamma }_{010}Postresidential+u_{0j0})\\ +\hspace{0.17em}({\gamma }_{100}+{\gamma }_{110}Postresidential+u_{1j0})BSFT+r_{ij0}]\\ +[({\gamma }_{001}+{\gamma }_{011}Postresidential+u_{0j1})\\ +\hspace{0.17em}({\gamma }_{101}+{\gamma }_{111}Postresidential+u_{1j1})BSFT\\ +\hspace{0.17em}{r}_{ij1}]\cdot a_{ijt}+{\varepsilon }_{ijt}\end{array}$$

or,

$$\begin{array}{l}{y}_{ijt}=[({\gamma }_{000}+{\gamma }_{010}Postresidential+{\gamma }_{100}BSFT\\ +\hspace{0.17em}{\gamma }_{110}Postresidential*BSFT)\\ +\hspace{0.17em}({\gamma }_{001}{a}_{ijt}+{\gamma }_{011}Postresidential*a_{ijt}\\ +\hspace{0.17em}{\gamma }_{101}BSFT*a_{ijt}+{\gamma }_{111}Postresidential\\ *\hspace{0.17em}\text{BSFT\hspace{0.17em}}*{\text{a}}_{\text{ijt}})+({\varepsilon }_{\text{ijt}}+{\text{u}}_{\text{0j0}}+{\text{u}}_{\text{1j0}}*\text{BSFT}\\ +\hspace{0.17em}{u}_{0j1}*a_{ijt}+u_{1j1}*BSFT*a_{ijt}+r_{ij0}+r_{ij1}*a_{ijt})\end{array}$$

This model will be estimated using either SAS Proc Mixed (or Proc NLMixed if a nonlinear link function is necessary).

Test of hypothesis

In the absence of significant postresidential interactions with BSFT treatment (γ₁₁₀ = γ₁₁₁ = 0), the test of the hypothesis is a test of the significance on the coefficients on the BSFT term alone from the intercept equation, γ₀₀₀, and the term that includes BSFT interacted with a_ijt from the equation for the slope of the growth curve, γ₀₀₁. If γ₀₀₀ is significantly less than zero, then BSFT participants (on average across all the treatment sites) will have achieved lower drug use immediately post intervention than did the treatment as usual participants. If γ₀₀₁ is significantly less than zero, then BSFT participants (on average across all treatment sites) will have had a decrease in drug use relative to the treatment as usual participants from immediately post intervention to eight and 12 months post intervention. Conversely if γ₀₀₀ and γ₀₀₁ are significantly greater than zero, then BSFT participants will have, respectively, greater drug use immediately post intervention and greater increase in drug use relative to treatment as usual participants. To simplify the presentation and interpretation of results, planned contrasts will also test if there are differences between BSFT and treatment as usual at eight and 12 months.

In the case of a significant postresidential interaction with BSFT treatment, each of the modalities will be tested for effectiveness of BSFT separately, using a slightly different parameterization from above. In this parameterization, the intercept terms of each of the equations will be suppressed and separate coefficients for the effectiveness of BSFT for each modality will be estimated. Thus, the effectiveness of BSFT can be tested in a single model for both modalities. In addition, a planned post hoc analysis will test for the effectiveness of BSFT in separate analyses by modality with site parameterized as a fixed effect.

Advantages of statistical model

There are several advantages to this approach. First, in the test here, a_ijt is the time (in 28 day “months”) since four months postrandomization. Thus, assessments are not required to be at the same or at equally spaced intervals across individuals. Second, because randomization will occur toward the end of residential treatment (and just before postresidential services – BSFT or treatment as usual – are to begin), the model only includes data from the 2nd through 12th assessments and controls for the baseline amount of drug use. Thus, the comparison is of time postrandomization for both modalities. That is, both residential and outpatient participants will be aligned (on average) with respect to the time since randomization at follow up. This will facilitate post hoc comparisons of the effectiveness of BSFT across the two groups, outpatient and residential.

Note that as the model is parameterized, it allows for different trajectories of outcome by modality. Whereas differences in the effectiveness of BSFT will be tested by modality, it is possible for the trajectory of an outcome to differ by modality and for the effect of BSFT to be the same across these two modalities. This is shown in Figure 1. As shown, the trajectories and direction of change are indeed different by modality, however the effect of BSFT is the same – it reduces the amount of drug use relative to treatment as usual.

Figure 1.

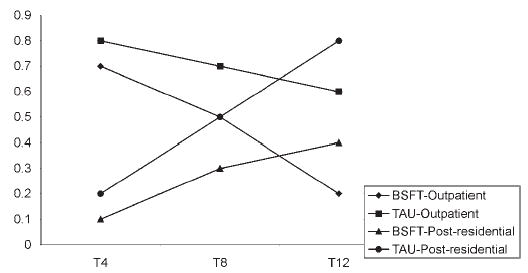
Drug use over follow-up.

This model does make several assumptions. First, that the underlying data are conditionally normal (a nonlinear link function is available, if necessary in Proc NLMixed). Second, the model also assumes that random effects are conditionally normal. The analysis results will be examined for the reasonableness of these assumptions. Should sufficient deviations from the normality assumptions be found, alternative, nonparametric estimation of random effects will be explored [22,23].

Sample size and statistical power

Prior research on BSFT has shown simple (standardized difference) effect sizes in the range of 0.56 to 0.68 for drug use, problem behaviors and family functioning. Power analysis for the planned hypotheses are based on the work of Raudenbush and Liu [18], which describe a model for use with a simple effect in a multisite clinical trial where the treatment site is treated as a random effect and there is variability in the effectsize across treatment sites. This model assumes equal numbers of participants at each site. To enhance the generalizability of findings, sites with smaller potential caseloads will not be excluded, thus, the number of participants per site will vary. In addition, if smaller samples are balanced with equal numbers of proportionately larger samples, it will be possible to examine these larger sites separately, in a post hoc analysis. Because variable site size is the limiting case for power, the case of variable numbers per site is presented.

In both cases the same methodology to estimate power is used; however, in the case of varying numbers per site, an adjusted n per site is utilized. Following the recommendations of Cohen [24], when there is variability in sample sizes across conditions, a harmonic mean of the individual sample sizes is computed. The harmonic mean weights the mean more to the smaller sample sizes. Once the harmonic mean is calculated then power estimation continues in the normal fashion. This is clearly an approximation, but should be sufficient for trial planning.

From examining multiple configurations, 14 sites with approximately 60 participants per site, on average, are proposed. This results in a total sample size of 840. If there are equal numbers of sites with 30, 60 and 90 participants, for example, the harmonic mean of the individual site sizes is 49 per site. Thus, there is an 11 subject per site penalty for allowing the sites to vary in size. [Note, there is equal power to uncover effects with 14 sites with 49 subjects each, as long as all sites had exactly 49 subjects; total sample = 686). With the proposed sample configuration (n = 60, J = 14, effective n = 49), there is nearly 90% power to uncover main effects of treatment in the range of effect sizes expected (0.4 to 0.6). Power to uncover significant modality effects on this main effect of treatment (a covariate explaining treatment variability) is over 80% for most effect sizes in the range 0.75–1.0. Note that the variability of treatment effects is the base for modality X treatment interactions. The following sections describe these calculations in more detail.

Main effect of treatment (treatment X time interaction)

Figure 2 (prepared using the OptDes software provided by Dr Steven Raudenbush) shows the expected power to uncover a significant overall treatment effect when there are 14 sites (J = 14), the average treatment effect varies from 0.4 to 0.6 (δ = 0.40, δ = 0.50, δ = 0.60), and the variability in this effect size is either small, moderate or large (σ_δ² = 0.05, 0.10, and 0.15; as coined by [18]). As can be seen in the graph, at the point of 49 subjects per site, there is over 90% power to uncover an average effect size in all combinations except for the smallest average effect size with the large variability in effect size (δ = 0.4, σ_δ² = 0.15), where the power is approximately 82%. Note that all 840 subjects are included in the power analysis because the analysis format will allow incorporation of all subjects randomized, regardless of the amount of follow up available on these subjects. With monthly follow up on the primary outcome, most participants will provide an estimate of change in drug use.

Figure 2.

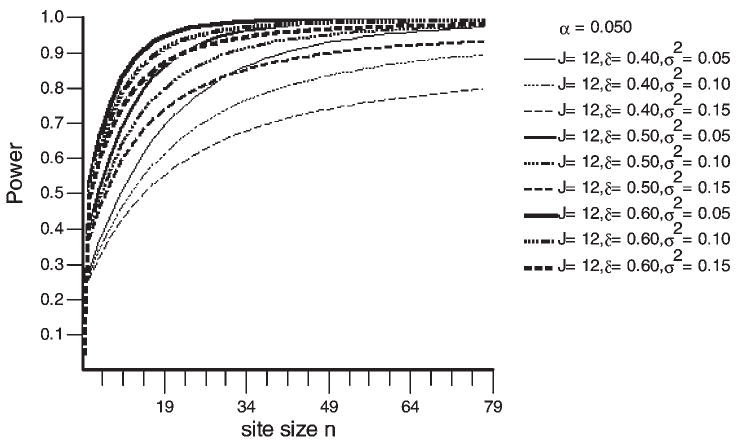
Power for main hypothesis.

As can be seen in Figure 2, site variability in effect sizes may have a substantial effect on power. If the power calculations above are compared with a simple repeated measures power analysis in which there is no variability in effect sizes across sites, there is over 80% power to uncover a considerably smaller standardized effect size. The program described in Hedecker, Gibbons and Waternaux [25] is used to calculate power in the case with no variability of effect size across sites. In this case, there is over 90% power to uncover a condition X time interaction with an effect size of 0.25 at the last time of assessment. This estimate assumes 10% attrition at each assessment, a linear growth curve and minimal residual correlation across time (P = 0.1). Power actually increases as the correlation of measures across time increases. It is not uncommon for measures such as those used to test the hypotheses in this trial to have correlations across time in the range of 0.2 to 0.4, so power may be better than described here. Clearly, if site variability is smaller than the estimates in the graph above, there is substantially more power. On the other hand, if site variability is higher than the estimates in the graph above, there is substantially less power.

Separate analysis by residential/outpatient status

The planned primary test of the difference in post-residential versus outpatient status, the effect size is measured as a standardized function of the variability in the effect size. Similarly, other planned post hoc analyses that explain the variability in effect size are expressed in this metric. Table 1 was created using the SAS program in the appendix of Raudenbush and Liu [18]. It shows the power associated with various effect sizes of the covariates. The primary covariate to be considered will be modality (postresidential/outpatient). Assuming that there is moderate variability in the effect of BSFT across sites [V(d) = 0.10 in Table 1], then there will be over 86% power to uncover an effect of modality that is 0.75 of a standard deviation in the effect size. If the mean effect of treatment is 0.5, this would imply that there is more than 86% power to uncover a significant difference by modality with an effect size in the less effective modality of 0.38 [ = 0.5–(0.75 × 0.32)/2] and an effect size in the more effective modality of 0.62 [=0.5 + (0.75 × 0.32)/2]. For the modality with the smaller effect size, power is considerably less than 80% when site variability is estimated using a random effect. However, when site variability is estimated as a fixed effect, there is over 80% to uncover a significant effect in a particular modality for any effect size that is equal to or greater than 0.20.

Table 1.

Power to uncover covariate effect on treatment effect

		Effect size of covariate effect
V(d)	SD(d)	0.75	0.80	1.00
0.05	0.22	0.94	0.97	0.99
0.10	0.32	0.86	0.90	0.98
0.15	0.39	0.76	0.81	0.95

Summary and suggestions for future research

BSFT is an effectiveness protocol within the Clinical Trials Network of the National Institutes on Drug Abuse. The BSFT study is conducted within the context of increased interest in effectiveness research across a number of disciplines. However, because there are little established or accepted criteria with regard to the differences between effectiveness and efficacy trials, the language used to describe and the procedures used to conduct this type of trial have not been standardized. Nonetheless, we believe that three aspects of the BSFT trial exemplify the mission of effectiveness trials and help to distinguish this research from prior BSFT efficacy trials. These aspects include: 1) a more heterogeneous study population, 2) the estimation of site effects and site by treatment interactions as random effects, and 3) the comparison of BSFT to the specific treatment as usual associated with each site. The cost of these design elements is a larger trial than would be required merely to establish efficacy. The benefits of these design elements are: 1) the ability to generalize the results to clinics outside of the trial sample with statistical credibility, and 2) increased ecological validity to individual clinic management. This type of design has the potential to have far greater impact on clinical practice because of the direct comparison of the new “experimental” treatment to multiple existing treatments (variable treatment as usual).

In planning this trial, several areas for future research were identified. First, there is a need for studies examining the strengths and weaknesses of different approaches for examining effectiveness across sites. Whereas the statistical literature is quite clear on implications of various approaches this is not reflected in the behavioral literature. In addition, because few multisite studies have been conducted in behavioral sciences, there is a dearth of published studies documenting the level of variability in treatment effects across sites. Second, there are very few algorithms or computer programs available for estimation of power with multiple random effects. Specifically, algorithms are needed for multilevel power calculations with non-normal and/or noncontinuous outcomes. Estimation of the power curves is already possible using simulation methodology [25]; however, more published reports that provide the full details of the estimated statistical model (i.e., estimates of all variance components associated with random effects) are needed to provide the context in which to perform these simulations. Publication of complete documentation of trial results and analyses of currently running behavioral effectiveness studies will facilitate future planning of these frequently complex protocols.