Heritability of fitness in a wild mammal population

Abstract

Classical population genetics theory predicts that selection should deplete heritable genetic variance for fitness. We show here that, consistent with this prediction, there was a negative correlation between the heritability of a trait and its association with fitness in a wild population of red deer (Cervus elaphus) and there was no evidence of significant heritability of total fitness. However, the decline in heritability was caused, at least in part, by increased levels of residual variance in longevity and, hence, in total fitness: in this population, longevity is known to be heavily influenced by environmental factors. Other life history traits that were not associated with longevity, such as average annual breeding success, had higher heritabilities. Coefficients of additive genetic variance differed markedly between traits, but highly skewed measures, such as male breeding success, generally had greater coefficients of variance than morphometric traits. Finally, there were significant maternal effects in a range of traits, particularly for females.

Fisher's fundamental theorem of natural selection predicts that the rate of change of mean fitness in a population should be equal to the additive genetic variance in fitness (1). By extension, in a population at equilibrium there should be no heritable variation for fitness, because alleles conferring fitness benefits should have increased in frequency until they reached fixation, whereas those associated with low fitness should have been reduced and eventually lost from the population. The theorem has been extrapolated further to suggest that the amount of additive genetic variance for a trait—and hence its heritability—should decrease with the trait's association with fitness (2, 3). In support of these expectations, in a review of 1,500 heritability estimates from Drosophila studies, Roff and Mousseau (4) report that “life history” traits such as fecundity and viability, subject to strong directional selection, have lower heritabilities than morphological and physiological traits, which presumably are under weaker selection. A second review of 1,120 heritability estimates from wild outbred populations of 75 species reached similar conclusions (5), but direct evidence of the relationship between total fitness and heritability in natural populations is scarce—presumably because of the considerable difficulty of estimating both measures in the wild. In one notable exception, Gustafsson (6) demonstrated that in collared flycatchers (Ficedula albicollis), there was a negative relationship between the heritability of a trait and its association with fitness.

Higher heritability in morphological than in life history traits may not, however, represent the depletion of genetic variation that results from selection. The heritability of a trait is defined as the proportion of the total phenotypic variance that can be ascribed to additive genetic variance (2). Its magnitude therefore partly depends on the relative contribution of nongenetic factors to the total variation, so traits that are influenced heavily by environmental factors will, by definition, show low heritabilities (7–9). For example, measures of total fitness in a multiparous organism will be associated with longevity, which is likely to be influenced heavily by environmental factors and stochastic variation, inevitably generating a low heritability. Furthermore, differing levels of nonadditive genetic variance will also affect heritability estimates (8). Levels of dominance and epistatic variance may vary consistently between traits (10, 11): for example, life history traits appear to exhibit higher levels of dominance variance than morphometric traits (12).

Where levels of other components of variance differ between traits, the coefficient of additive genetic variance (CV_A) may provide a more informative measure of additive genetic variation than the heritability (3, 7). The CV_A scales the component of additive genetic variance by the trait mean instead of by the total variance and so is not confounded by the magnitude of other variance components. Under either directional or stabilizing selection, levels of CV_A can be related directly to the response to selection, or “evolvability,” of a trait (7, 13). In contrast to the implications of Fisher's theorem, there is evidence that CV_A values are higher for life history traits than for morphological traits (7)—possibly because life history traits are likely to be affected by a larger number of loci and, thus, have higher mutational input. Furthermore, if they are influenced by numerous underlying metric traits for which there is ample additive genetic variation, it can be argued that they cannot have low genetic variation (9). Thus, although strong directional selection should deplete additive genetic variation, there may be several other processes maintaining genetic variation in life history traits (14).

In this paper, we compare the components of variance in three morphological and four life history traits (including lifetime breeding success) in a wild mammal population to assess whether or not the level of additive genetic variance in a trait reflects the strength of selection to which it is subject. We test the predictions of the corollary of Fisher's fundamental theorem, that there should be no additive genetic variance for total fitness, against the more recent suggestions (7) of substantial additive genetic variance in life history traits. We use data from an unmanaged population of red deer (Cervus elaphus) on the Isle of Rum, Scotland, which has been the subject of intensive, long-term study (15).

Studies of quantitative genetics in wild populations traditionally have used parent–offspring or sib regression analyses, which cannot simultaneously incorporate information from a variety of relationships of different degrees, such as offspring, parents, grandparents, full-sibs, and half-sibs. Recent developments in animal breeding science of analytical techniques based on restricted maximum-likelihood (REML) estimates and general mixed models (in particular, the “animal model”) use all pedigree information, making them considerably more powerful than traditional approaches (10). They invoke fewer assumptions, for example, about selection patterns or inbreeding, and do not require balanced data sets, making them more amenable to data from natural populations (refs. 16 and 17; J. M. Milner, S.B., J.M.P., and S. D. Albon, unpublished results). We describe here the partitioning of the total phenotypic variation in a trait into its additive genetic, maternal, and residual components using a REML-based analysis. We conduct separate analyses for males and females, because of marked differences between the sexes in the shape of trait distributions, in the selection pressures to which they are subject and, third, in the effects of environmental factors (e.g., refs. 15 and 18–20). For all traits, we compare the information imparted by estimates of heritability and the coefficients of variation.

Methods

Study Population.

All animals in the unmanaged red deer population in the North Block of the Isle of Rum, Inner Hebrides, Scotland, are individually recognizable and have been monitored intensively since 1971. Culling of the population ceased in 1973, resulting in an increase in the number of adult females but decrease in the number of adult males; since 1982, the population has remained relatively stable around a mean value of 162 females (± 16 SD) and 109 males (± 17 SD), representing an overall increase in adult deer of approximately 20%. Approximately 60% of calves were caught soon after birth, and a blood sample was taken for genetic analysis; other individuals were sampled post mortem or by immobilization. All sampled deer were genotyped at up to three locus-specific protein and nine microsatellite markers (21). Further details of the study area and population are given in refs. 15 and 18–20.

Pedigree Determination.

Because calves remain with their mothers for at least 1 year, maternity was determined from field observations for a total of 2,270 individuals (no conflicts with genetic data were encountered). Paternity was assigned for 840 of these using a combination of genetic and behavioral data. The fathers of 555 calves were identified from genetic data using a likelihood-based analysis program, cervus (21), which determines a criterion for paternity likelihood scores above which a given paternity will be correct in 80% of cases. Among the remaining calves, for which paternity could not be assigned from genetic data, 285 paternities were identified from behavioral data. A male was assigned paternity of a calf if the mother was seen to be in estrus while in his harem or if she was in his harem for at least 6 days of an 11-day window around the estimated conception date [calculated by backdating from the date of birth (15, 22)]. These behavioral criteria identify the correct father in approximately 70% of cases (23).

The study population consisted of 36 matrilines derived from adult females alive in 1971 and ranging in size from 6 to 149 individuals, with up to eight generations within a matriline over the study period. Offspring of individual males were distributed over several matrilines, creating an interconnected pedigree containing a total of 2,374 individuals. The variance component estimation procedure described below incorporates information from all available relationships in a pedigree, making it considerably more powerful than traditional, pairwise-regression analyses (10). Errors in paternity assignment inevitably will have reduced estimates of the covariance between relatives and, hence, of heritability, but because the number of maternal connections was almost three times the number of paternities, we assume that the effect was minimal.

Traits Studied.

We estimated the components of variance of the following 18 traits, for which means, SDs, and sample sizes are given in Table 1.

Table 1.

Means, SD, sample sizes (N), variance components, heritabilities (h²), and correlation with total fitness (r) for all traits considered

Trait	Mean	(SD)	N	VA (SE)	VM (SE)	VR (SE)	h2	(SE)	r
Life history traits
Females
Total fitness	2.91	(3.57)	360	0.000  (0.000)	1.037  (0.281)	5.388  (0.350)	0.000	(0.056)	1.000
Adult BS	5.18	(3.31)	202	0.000  (0.003)	1.499  (0.728)	7.283  (0.767)	0.000	(0.003)
Longevity	6.42	(5.93)	360	0.000  (0.000)	5.304  (1.337)	23.376  (1.530)	0.000	(0.054)	0.949
Adult longevity	11.52	(3.85)	202	0.001  (0.002)	0.739  (1.459)	12.388  (1.459)	0.000	(0.001)
Fecundity	75.82	(14.05)	161	95.185  (34.281)	10.489  (8.430)	100.839  (28.340)	0.461	(0.150)**	0.230
Age at first breeding	4.00	(0.76)	254	0.174  (0.075)	0.041  (0.041)	0.379  (0.068)	0.293	(0.120)*	0.324
Males
Total fitness	2.09	(5.57)	362	0.434  (0.681)	0.000  (0.000)	21.523  (1.262)	0.020	(0.060)	1.000
Adult BS	6.45	(8.25)	116	4.294  (3.922)	0.000  (0.004)	47.011  (5.867)	0.084	(0.076)
Longevity	3.14	(3.27)	362	0.060  (0.808)	1.565  (0.452)	7.765  (0.867)	0.006	(0.086)	0.614
Adult longevity	10.55	(2.54)	116	0.000  (0.003)	0.000  (0.004)	4.702  (0.445)	0.000	(0.001)
Maximum annual BS	3.70	(3.36)	93	0.784  (1.313)	0.000  (0.002)	7.408  (1.520)	0.096	(0.160)	0.828
Age at first breeding	6.24	(1.55)	121	0.480  (0.750)	0.000  (0.000)	1.986  (0.737)	0.194	(0.300)	0.303
Morphometric traits
Females
Birth weight, kg	6.38	(1.22)	609	0.371  (0.1087)	0.299  (0.067)	0.812  (0.084)	0.250	(0.071)**	0.160
Leg length, mm	186.49	(7.82)	120	18.684  (10.3672)	8.400  (6.629)	23.182  (9.828)	0.372	(0.168)*	0.206
Jaw length, mm	255.34	(8.42)	144	32.287  (15.3059)	2.742  (7.482)	26.620  (15.769)	0.524	(0.218)**	0.023
Males
Birth weight, kg	6.69	(1.24)	673	0.165  (0.0992)	0.414  (0.067)	0.911  (0.078)	0.112	(0.067)*	0.182
Leg length, mm	193.57	(7.73)	91	3.935  (9.3673)	0.102  (0.215)	50.720  (11.723)	0.072	(0.144)	0.426
Jaw length, mm	271.42	(7.88)	109	37.462  (7.2996)	9.024  (6.795)	15.812  (1.371)	0.601	(0.117)**	0.029

The total variance was partitioned into additive genetic variance (V_A), maternal effect variance (V_M), and residual variance (V_R). BS, breeding success; leg length, metatarsal length. *, P < 0.05; **, P < 0.01. 

Life History Traits.

(i) Total fitness.

An individual's total fitness was defined as the number of offspring it produced in its lifetime. For animals that survived to breeding age, this was given by the adult breeding success, defined below. Animals that died before breeding were assigned a fitness score of zero, so the measure represented an entire lifetime for every individual in the population. Although number of offspring may be only an approximation of total fitness in this age-structured population, it is the closest the data allow to a more exact measure (24).

(ii) Adult breeding success.

As well as total fitness, which was measured for all individuals in the population, we also considered adult breeding success, restricted to individuals who reached breeding age. The breeding success of females was defined as the total number of calves a female gave birth to in her lifetime. The breeding success of males was defined as the number of calves sired, using more relaxed criteria than for the pedigree determination and based only on behavioral data gathered during the mating season (the rut). Using the paternity assignment method described above would underestimate the breeding success of ungenotyped stags and would not make use of the data on the 819 calves whose paternities could not be resolved with sufficient resolution to be included in the pedigree. A male was assumed to be the father of a calf if its mother was seen to be in estrus while in his harem or if she was in his harem for longest during an 11-day window around her estimated conception date (15, 22). We justify this approach on the grounds that, even if more paternities are misassigned, estimates of breeding success calculated this way represent a male's prowess during each rut and are a reliable indicator of relative breeding success (22). Males who were seen rutting but who were not assigned any paternities were given a lifetime breeding success of zero. Considering males born since 1982 for whom there were adequate genetic data, the correlation between a male's total breeding success estimated this way and total breeding success estimated from genetic data (21) was 0.86 (n = 72).

(iii) Longevity.

Total longevity was the age in years at which an individual died. More than half of individuals died before reaching breeding age, so we also considered adult longevity, defined as longevity of 3 years or more.

(iv) Female fecundity.

Female fecundity (or average annual breeding success) was defined as the percentage of years of her breeding lifespan that a female produced a calf; this ranged from 50% to 100%. Only females that had reached at least 6 years of age were included in this measure to ensure that it represented several possible breeding attempts.

(v) Male maximum annual breeding success.

Because male breeding success varies with age, a male's maximum value in any 1 year was considered instead of an average measure. Only males that reached 7 years of age were included, because none reached their peak before this age.

(vi) Age at first breeding.

The age at which a female first gave birth to a calf or at which a male first sired a calf was analyzed for each sex.

Morphometric Traits.

(vii) Birth weight.

Calves were caught and weighed within 14 days of birth, and birth weight was estimated by back-calculating from the weight at capture, assuming a gain of 0.015 kg/hr since birth (15).

(viii and ix) Adult jaw and hind leg length.

Jaws and hind legs were removed at death, and the length, in millimeters, of the dry bone was measured. For jaws, this was the distance from the outer point of the fourth incisor socket to the posterior edge. For hind legs, the length of the metatarsus from proximal and distal metatarsal canal was measured. Only measures on adults (taken as 3 years or older) were used.

For traits i–v, analysis was restricted to individuals for whom complete life history data were available. This precluded any dying from unnatural causes, such as those being shot outside the study area or dying as a result of an accident. Only cohorts born before 1987 were considered, because data on more recent animals would be biased toward those dying young. The other traits were not restricted in this way.

Variance Component Analysis.

Variance components and heritability values were estimated using a multivariate restricted estimate maximum likelihood procedure (VCE; refs. 25 and 26). An “animal model” was fitted in which the phenotype of each individual was broken down into its components of additive genetic value and other random and fixed effects:

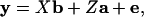where y was a vector of phenotypic values, b and a were vectors of fixed and random effects, e was a vector of residual values, and X and Z were the corresponding design matrices (16, 27).

For all traits, maternal identity was fitted as a random effect to prevent shared maternal environment being mistaken for shared genetic effects. Animals were removed from the data set in cases in which it was impossible to distinguish the two. This involved maternal half-sibships in which no paternities had been assigned and neither the mother nor any of the calves were related to any other individuals in the pedigree, and it resulted in the exclusion of 12 animals. Age was fitted as a fixed effect in the models of leg length and jaw length. Area was fitted as a fixed effect in all models: an individual was assigned to one of four areas in the study site (15) based on the average coordinates at which it had been seen in censuses throughout its life. The exception to this was female jaw length, for which VCE runs incorporating area as a fixed effect did not converge, and which, therefore, was analyzed without the area-fixed effect.

The total phenotypic variance (V_P) of a trait can be described as V_P = V_A + V_M + V_R, where V_A is the additive genetic variance, V_M is the maternal effect variance, and V_R is the residual variance, consisting of environmental effects, nonadditive genetic effects, and error variance (2). Because only 124 of the 2,374 (≈5%) individuals in the pedigree belonged to a full sibship, any dominance variance is unlikely to have affected estimates of additive variance. We did not attempt to assess the total contribution of nonadditive genetic variance to the residual variance because this would have required considerably more power in our pedigree information.

The narrow-sense heritability (2), or the resemblance between parent and offspring values, is defined by the ratio of the additive genetic variance to the total phenotype variance: h² = V_A/V_P. Similarly, the maternal effect was quantified as m = V_M/V_P. We also estimated the CV_A, for which the respective variance component was scaled by the trait mean (X̄) rather than the total variance: CV_A = 100 × 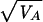/X̄. The coefficient of residual variance (CV_R) was calculated similarly. Estimates were taken from univariate runs, with analyses performed separately for males and females (see Introduction). When a maternal effect was not significantly different from zero, we reran the analysis without it. Because this did not have a significant effect on any of the estimates of heritability or CV_A for any of the traits, we present only the results with the maternal effect included.

Although the restricted estimate maximum-likelihood procedure assumes that residuals from a model of fixed and random effects follow a normal distribution, it is fairly robust to departures from normality: deviations from normality may affect optimality properties, but estimates remain unbiased (ref. 28; see also ref. 29). However, because traits i–iii and v were not distributed normally, we compared analyses of untransformed and log-transformed values. There were no significant or consistent differences between heritability estimates on either scale. Because coefficients of variance are meaningless for transformed data (7), we report here the analysis of the untransformed data.

Instead of simply defining a trait as “life history” or “morphometric” (e.g., as in ref. 4), we can quantify its association with total fitness—and hence the selection to which it is subject—by the correlation r between the trait and total fitness. Spearman rank correlations r_s between r and heritabilities or CV_A values were estimated separately for each sex and excluded adult longevity and adult breeding success because these were merely subsets of total longevity and total fitness. This gave seven data points for each test. For age at first breeding, which was negatively correlated with total fitness, r was multiplied by −1 so that it would scale positively with total fitness like the other life history traits.

The VCE program returns SEs for the variance components and heritability estimates, from which significance was assessed by t tests. SEs for the coefficients of variation were calculated by using the formula given in ref. 30 (p. 138). To assess the correlations' significance, we randomized the values for each trait and recalculated r_s a total of 50,000 times, with the significance P representing the proportion of r_s values with absolute magnitude greater than that of the observed value. All statistical tests were two-tailed.

Results

Heritabilities.

Estimates of heritability (h²) ranged from 0.000 for adult longevity in both sexes to 0.601 for male jaw length (see Table 1). Among the 12 life history traits considered, only female fecundity and female age at first breeding were significantly different from zero, although age at first breeding had a heritability of nearly 20% in males. In contrast, all three female morphometric traits and two of the three male morphometric traits had heritability estimates significantly greater than zero.

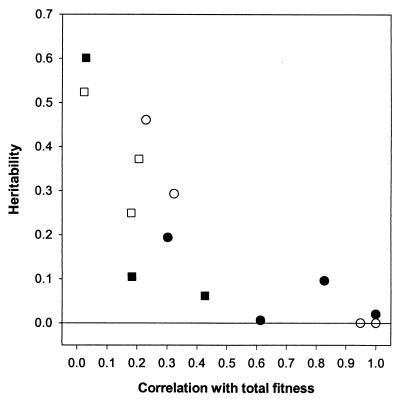
In each sex, there were significant negative correlations between h² of a trait and its correlation with total fitness, r, given in Table 1 (Spearman rank correlation: females, r_s = −0.758, n = 7, P = 0.044; males, r_s = −0.786, n = 7, P = 0.043). Fig. 1 shows the relationship between h² and r.

Figure 1.

Heritability estimates plotted against each trait's correlation with total fitness, r (r = 1.0 for total fitness). ○, Female life history traits; □, female morphometric traits; ●, male life history traits; ■, male morphometric traits.

Coefficients of Variance.

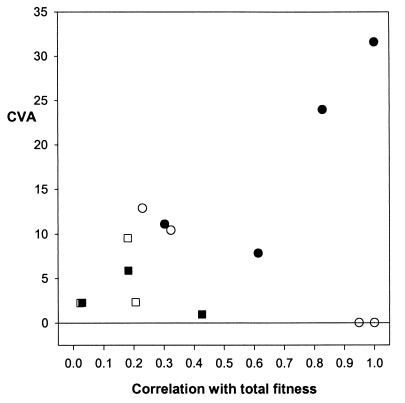
The coefficients of additive genetic variance ranged from 0.000 for longevity and female total fitness and 1.025 for male leg length to 32.11 for adult breeding success in males (see Table 2). Because life history traits had both the lowest and highest CV_A values, there was no suggestion of a consistent difference between life history traits and morphological traits. Fig. 2 shows CV_A plotted against the correlation with total fitness, r. The correlation between r and CV_A was negative for females (r_s = −0.396, n = 7, P = 0.353) and positive for males (r_s = 0.714, n = 7, P = 0.081), but not significant in either case.

Table 2.

Coefficients of CV_A, of residual variance (CV_R), and of maternal effect (m)

Trait	CVA	(SE)	CVR	(SE)	m	(SE)
Female trait
Total fitness	0.000	(0.000)	79.888	(4.492)	0.161	(0.041)**
Adult BS	0.000	(0.000)	52.115	(3.221)	0.171	(0.079)*
Longevity	0.000	(0.000)	75.284	(4.098)	0.185	(0.089)*
Adult longevity	0.275	(0.014)	30.562	(1.736)	0.056	(0.043)
Facundity	12.868	(0.729)	13.244	(0.751)	0.051	(0.095)
Age at first breeding	10.461	(0.467)	15.395	(0.699)	0.068	(0.068)
Birth weight	9.543	(0.276)	14.123	(0.413)	0.202	(0.042)**
Leg length	2.318	(0.151)	2.582	(0.168)	0.167	(0.102)
Jaw length	2.225	(0.133)	2.021	(0.121)	0.044	(0.120)
Male trait
Total fitness	31.583	(1.286)	222.437	(27.288)	0.000	(0.000)
Adult BS	32.113	(2.306)	106.253	(12.537)	0.000	(0.000)
Longevity	7.832	(0.293)	88.803	(5.298)	0.167	(0.045)**
Adult longevity	0.000	(0.000)	20.551	(1.298)	0.000	(0.000)
Maximum annual BS	23.936	(1.853)	73.583	(7.787)	0.000	(0.000)
Age at first breeding	11.098	(0.734)	22.588	(1.550)	0.000	(0.000)
Birth weight	5.888	(0.161)	14.265	(0.397)	0.280	(0.041)**
Leg length	1.025	(0.070)	3.679	(0.273)	0.002	(0.004)
Jaw length	2.255	(0.153)	1.465	(0.099)	0.145	(0.121)

BS, breeding success; leg length, metatarsal length. *, P < 0.05; **, P < 0.01. 

Figure 2.

CV_A plotted against each trait's correlation with total fitness, r. ○, Female life history traits; □, female morphometric traits; ●, male life history traits; ■, male morphometric traits.

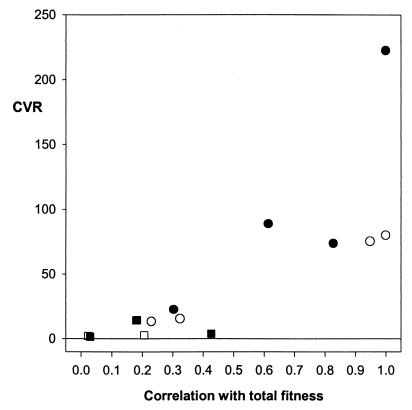
In contrast, the CV_R increased significantly with a trait's association with fitness (females, r_s = 0.893, n = 7, P = 0.007; males, r_s = 0.857, n = 7, P = 0.023); see Fig. 3.

Figure 3.

CV_R plotted against each trait's correlation with total fitness, r. ○, Female life history traits; □, female morphometric traits; ●, male life history traits; ■, male morphometric traits.

Maternal Effects.

There were significant maternal effects (m) on total fitness and adult breeding success in females (see Table 2). Mother's identity also had a significant effect on total longevity and birth weight in both sexes. None of the other traits showed significant maternal effects, and removal of maternal effects from the models in which they were not significant did not affect the estimates of additive genetic variance components.

Discussion

Fisher's fundamental theorem of selection predicts that the change in mean fitness resulting from selection should be equal to the additive genetic variance in fitness (1). The prediction itself requires fairly specialized conditions, but has a more widely applicable corollary: in a population at equilibrium unaffected by mutation or by changes in the environment, there should be no additive genetic variance of fitness (see ref. 31 and references therein). However, the input of mutational variance is a certainty, and, particularly in natural populations, environmental inconstancy is extremely likely. Knowledge of the relative effects of these processes on the heritability of fitness is therefore crucial for an understanding of natural selection and evolution (32); one particular manifestation is the problem that a lack of heritability of fitness poses for theories of mate choice and sexual selection (3, 32–35). In this population, heritability declined with the proportion of total fitness explained across a suite of traits. Estimates for the amount of additive genetic variance for fitness did not differ significantly from zero, whether fitness was measured as the breeding success across all individuals in the population or just for those who reached breeding age. Is this, as in ref. 6, empirical support for Fisher's fundamental theorem?

Total fitness in red deer is closely associated with longevity (here, r = 0.95 in females, r = 0.61 in males). The additive genetic variance in longevity was not significantly greater than zero either for adult or for total longevity in either sex, but longevity had a high component of residual variance. Because longevity was measured in years, the residual variance probably contained a proportion of measurement error introduced by the rounding procedure. However, there will also have been a very substantial environmental component of variance generated by the effects of climatic conditions and population density on mortality in this population (e.g., refs. 18, 20, and 36). The stochastic variation in a single event such as death will also be greater than a mean of repeated measures, such as fecundity, or a trait that has been influenced by stochastic effects over an entire growth period or entire breeding lifespan. Thus, it is not clear whether the lack of additive genetic variance for longevity and, hence, for total fitness is caused by depletion by selection or whether the data simply lack the statistical power to detect any heritable variation given the amount of environmental noise. As in the few other comparable studies (see references in ref. 32), the standard errors on our estimates incorporate a range of heritability values. However, if there is nonzero heritability for total fitness in this population, the value is likely to be low.

The life history traits that did not directly incorporate longevity generally possessed heritabilities equivalent to the morphological traits and higher than those for longevity or total fitness. Female fecundity showed the highest heritability of any life history trait, at 0.46, and in both sexes about a fifth of the total variance in age at first breeding was the result of additive genetic variance. Coefficients of additive genetic variance for these measures were also correspondingly higher. Interestingly, similar patterns emerge from reviews of the Drosophila literature, with longevity having a low coefficient of variance but other life history traits having higher values (3, 14). Substantial levels of genetic variation therefore are being maintained in life history traits despite the directional selection to which they are subject—possibly because they are determined by many loci (7, 35) or because of antagonistic pleiotropy (14).

In accordance with the predictions in ref. 9 and the results in ref. 7, heritability estimates were significantly negatively correlated with the CV_R in females (r_s = −0.923, n = 7, P = 0.007) and nearly significantly in males (r_s = −0.741, n = 7, P = 0.0712). The significant correlations between CV_R and r (see Results) further confirm that high residual variance must have been dampening the heritability estimates for traits closely associated with total fitness. This change in the levels of residual variation argues for use of the alternative measure of heritable genetic variation, the coefficient of additive genetic variance (7). Although there was no clear relationship between a trait's CV_A and its correlation with total fitness, the six highest CV_A values were for life history traits (Table 2). Lifetime breeding success and its components have highly skewed distributions (particularly in males), whereas the morphological traits showed more symmetrical distributions. In any strongly right-skewed distribution, the mean will be small relative to the variance, generating high coefficients of variance. If a trait is constrained never to be negative but has a relatively low mean, a high variance will necessarily generate a strong right skew and a higher coefficient of variance than for a trait with similar variance but less skew. Thus although the CV_A is clearly a suitable measure of the “evolvability” of a trait (7), it is vulnerable to the confounding effects of the scaling factor in comparisons of variance components in traits with different distributions.

Finally, our results illustrate the prevalence of maternal effects on a range of traits. Birth weight, total longevity, and female adult breeding success and total fitness all showed significant maternal effects. The maternal effect on longevity was presumably because more than half of mortality is of juveniles, who will have shared their mother's environment throughout their lifespan. The higher frequency of maternal effects in female than male life history traits suggests that they were the result of females sharing home ranges of differing quality with their mothers (15) rather than, for example, differences between individuals in levels of maternal expenditure. There is a similar prevalence of maternal effects on morphometric traits in Soay sheep (J. M. Milner, S.B., J.M.P., and S. D. Albon, unpublished results), another species in which females tend to remain in matrilineal groups whereas males range more widely. For those traits with significant maternal effects, omitting the maternal component of variance would have artificially inflated the estimates of additive genetic variance.

To our knowledge, this is only the second free-living population for which the variance components of fitness have been estimated, with the collared flycatcher population on Gotland, Sweden, being the first (6). Several studies have reported the existence of heritable variation in traits closely associated with fitness (see reviews in refs. 4, 5, 7, and 13), but the heritability of total fitness may differ markedly from the sum of its parts: for example, there may be negative genetic correlations between different fitness components. Furthermore, the majority of such studies of traits closely related to fitness have involved laboratory or captive populations (e.g., refs. 37 and 38). Despite their undoubted logistical advantages, laboratory studies may suffer several drawbacks. First, fitness is measured in an artificial and potentially novel environment. Second, a relatively constant environment is likely to inflate estimates of heritability relative to values for wild populations (e.g., ref. 39). A tendency for laboratory stocks to be more inbred than natural populations or to have experienced a bottleneck probably will have affected levels of variation—although the direction of this effect is debatable (e.g., ref. 40). Finally, mating patterns may have been artificially controlled, again with unpredictable effects on the genetic variation. A comparative review of field and laboratory estimates of heritability found no evidence of a consistent difference between the two (41), but it is possible that this was caused by the above factors counterbalancing each other. The lack of comparable data from wild populations highlights the need for more studies of the heritability of fitness under natural conditions. With the availability of molecular data with which to determine pedigrees and the flexibility offered by maximum-likelihood analyses and the animal model, such studies should be increasingly feasible.

Abbreviations

CV_A

coefficient of additive genetic variance

CV_R

coefficient of residual variance

VCE

variance component estimation procedure