Abstract
Background
Multilevel models were designed to analyze data generated from a nested structure (e.g., nurses within hospitals) because conventional linear regression models underestimate standard errors and, in turn, overestimate test statistics.
Objectives
To introduce 2 types of multilevel models, the random intercept model and the random coefficient model, to describe the correlation among observations within a cluster, and to demonstrate how to identify the superior model.
Method
The conceptual and mathematical bases for the 2 multilevel model types are presented. Intraclass correlation is defined and assessment of model fit is detailed. An empirical example is presented in which average work hours per week and burnout are analyzed using data from 4,320 staff nurses clustered in 19 hospitals.
Results
Average work hours were positively associated with nurse burnout. The multilevel models corrected the problem of underestimated standard errors in conventional linear regression models. Graphs displaying the hospital-level differences illustrated the 2 multilevel model types. Although the multilevel models corrected the underestimation of standard errors, the results did not differ substantively for the conventional or the 2 multilevel models. The intraclass correlation coefficient was .044, indicating that the extent of shared variance among nurses in a hospital was low. The random intercept model fit the data better than did the random coefficient model.
Conclusions
Multilevel models provide a more accurate and comprehensive description of relationships in clustered data than do conventional models, by correcting underestimated standard errors, by estimating components of variance at several levels, and by estimating cluster-specific intercepts and slopes.
Keywords: clustered data, hierarchical structure, multilevel models
Observations of data collected from a hierarchical structure can be correlated with one another. Examples of hierarchical data are (a)-nurses nested within hospitals and (b) repeated measurements of the same person. In these instances, nurses and repeated measurements are at Level 1 and hospitals and persons are at Level 2 (Kreft & De Leeuw, 1998). With clustered data, estimated standard errors in a conventional regression are smaller than actual standard errors due to failure to account for the correlated structure of observations. This underestimation of standard errors causes an important problem, the increase of a Type I error, which implies a higher possibility of concluding that obtained results are significant, even though they may not be so (Reise & Duan, 1999).
Hence, the incorporation of correlated responses is crucial to obtain accurate results in the analysis. Multilevel models were developed to correct the dependency of observations within a cluster. Multilevel models have been popular among researchers in social and behavioral sciences because most data are generated from hierarchical structures (Kreft & De Leeuw, 1998; Raudenbush & Bryk, 2002).
Compared to the above disciplines, few studies in nursing have attempted to fix problems originating from correlated observations. The nursing researchers who have used multilevel models have focused on the effects of nurse staffing and nursing unit characteristics on patients' and nurses' outcomes (Cho, Ketefian, Barkauskas, & Smith, 2003; Mark, Harless, McCue, & Xu, 2004; Mark, Salyer, & Wan, 2000, 2003; McGillis Hall et al., 2003). Although Wu (1995) introduced multilevel models and Cho (2003) addressed the importance of multilevel modeling in nursing outcomes research, they did not detail various types of multilevel models nor did their examples contrast conventional regression results with the results of multilevel models.
The purpose of this article is to explore in depth the concept and use of multilevel models. First, multilevel models are introduced and two types are explained: the random intercept model and the random coefficient model. Second, the intraclass correlation (i.e., the amount of dependency among observations) and the method of choosing the better model in the comparison of two models are described. These concepts and methods are illustrated in a multilevel analysis of nurse survey data with a clustered continuous outcome. Nurse burnout is regressed on nurses' average work hours per week. The results of the two multilevel models are compared with those of a conventional linear regression model. Finally, graphs are provided that illustrate the sophisticated statistical treatment of clustered data that multilevel models offer.
Types of Multilevel Models
The conventional linear regression in Equation 1 presumes all observations are independent.
| (1) |
where α is the intercept, β is the effect of the covariate xi, and ei is the error term. The independence of observations signifies that the error terms for observations are unrelated to one another. The error terms, ei, are also assumed to be normally distributed with the mean of 0 and the variance of σ2 (Moore & McCabe, 2003).
If the values of yi are correlated as a consequence of the clustering of observations at a second level, the error terms among observations become correlated because the error term represents omitted factors in a model or measurement error in a dependent variable. The correlation of the error terms in clustered data violates the assumption in a conventional linear regression (Allison, 1999a). When this assumption is violated, the conventional regression does not perform well in estimating standard errors of coefficients. The correlated responses yield smaller standard errors of coefficients. Consequently, there is a higher possibility of obtaining falsely significant results (Allison, 1999b). Thus, the application of a multilevel model is appropriate due to the fact that multilevel models take into consideration the correlated structure of observations in the estimation of standard errors.
Multilevel models are divided into the random intercept model and the random coefficient model, based on how to treat an intercept and covariates. The random intercept model only considers the intercept as a random component, whereas the random coefficient model treats covariates as well as the intercept as random variables. It is also possible to treat only covariates as random variables. By treating the intercept and covariates as random components, the variation and effects of clusters can be examined (Kreft & De Leeuw, 1998). Contrary to the multilevel models, the conventional linear regression model does not consider the plausibility of similarity among observations in a cluster, and simply postulates that all the error terms are not related to one another. Here, the random intercept model and the random coefficient model are presented with an example of one covariate in a two-level structure.
Two-Level Random Intercept Model
The random intercept model (Equation 2) is the simplest type of multilevel model. Only the intercept is allowed to differ across clusters.
| (2) |
where yij is the dependent variable for observation i in cluster j, α is the intercept, β is the effect of the covariate xij, uj is the Level-2 random effect, and eij is the Level-1 random effect.
Equation 2 can be expressed in two equations based on a hierarchical structure. When equations 3 and 4 are combined, Equation 2 is obtained:
| (3) |
| (4) |
Unlike Equation 1, the random intercept model has two components of the intercept in Equation 4. α is the average intercept across all observations and all clusters, and uj is the amount by which the intercept of cluster j deviates from the average α. In Equation 2, eij is the error term associated with observation i in cluster j and uj is the error term of all the observations in cluster j. Therefore, among all observations in the same cluster, the error term uj is the same, but the error term eij could be different. In the random intercept model, the intercept β0j can vary across clusters, but the coefficient β of the covariate xij does not differ across clusters. Consequently, the intercept across clusters could be different but the slope across clusters would be the same (Healy, 2001). The random intercept model can also be considered to have two parts, fixed effects and random effects. In Equation 2,“α + βxij” does not change, regardless of observations and clusters, but “uj + eij” could change according to clusters and observations. Because of these characteristics, the former and the latter can be called fixed effects and random effects, respectively (Kreft & De Leeuw, 1998).
The random effects at the cluster level, uj, are assumed to have the mean of 0 and the variance of σu2. Also, the random effect in cluster j should not be correlated with either the random effects at the observation level, eij, or the random effect of other clusters. The assumptions related to eij are the same as those in the conventional linear regression model (Hox, 2002).
Two-Level Random Coefficient Model
In the random coefficient model (Equation 5), the slope and the intercept are allowed to vary across clusters.
| (5) |
where yij is the dependent variable for observation i in cluster j, α is the intercept, b is the effect of the covariate of xij, vj is the amount by which the coefficient of cluster j deviates from the average b, uj is the Level-2 random effect, and eij is the Level-1 random effect.
The random coefficient model in Equation 5 is obtained from the following three equations, consisting of one equation at Level 1 and two equations at Level 2:
| (6) |
| (7) |
| (8) |
The random coefficient model in Equation 5 differs from the random intercept model (Equation 2) because this model has two components of the effect of the covariate in Equation 8. b can be interpreted as the average of the covariate effects across clusters, and vj is the amount of deviation from the average covariate effect, b, in cluster j. Hence, in the random coefficient model, each cluster can have a different intercept and slope. In Equation 5, all clusters have the same values for the part “α + bxij,” but each cluster could have different values for the part “vjxij + uj + eij.” Thus, like the random intercept model, the random coefficient model is separated into fixed and random elements (Kreft & De Leeuw, 1998).
The random effect of a covariate at the cluster level, vj, is assumed to have a mean of 0 and variance σv2. Also, covariance between the random effects uj and vj is possible. Except for the assumption regarding the term vj and the allowance of covariance between uj and vj, all other assumptions in the random coefficient model are same as those in the random intercept model (Guo & Zhao, 2000).
Just as the conventional linear regression model sometimes includes multiple covariates, the random coefficient model with multiple covariates is also feasible. In addition, it is possible to treat several covariates as random variables at the same time. This makes it plausible to investigate the effects of several covariates at Level 2. However, there is a trade-off in using additional covariates. With additional covariates, more assumptions must be fulfilled and more parameters should be estimated (Hox, 2002). The assumptions and parameter estimation require more complex computations and therefore it will take longer to obtain results.
Characteristics of Multilevel Models
Multilevel models have three features that differ from conventional linear regression models. First, as noted earlier, the use of conventional regression for clustered data results in the underestimation of standard errors, because this model does not consider the similarity of responses among observations within the same cluster. Smaller standard errors affect test statistics, which are more likely to be statistically significant. Multilevel models resolve this problem by including random components of cluster effects in the statistical model. The consideration of random effects at the cluster level in the multilevel model makes it possible to estimate correct standard errors. By dividing the total variance in the dependent variable into between-cluster and within-cluster parts, the variability of random effects across clusters and the importance of clusters can also be evaluated (Teachman & Crowder, 2002; Wu, 1995).
Second, both observation-level and cluster-level covariates can be included in multilevel models. Owing to this feature, cross-level interactions (i.e., the relationship between observation-level and cluster-level covariates) can be examined. A cross-level interaction is useful for research questions about whether cluster-level characteristics moderate individual-level relationships. For example, country-level characteristics such as gross national product might moderate the individual-level relationship between women's educational attainment and fertility (Guo & Zhao, 2000; Hox & Kreft, 1994; Teachman & Crowder, 2002).
Third, aggregation bias might occur in the conventional linear regression model, but can be eliminated in multilevel models. Aggregation bias implies that the results from aggregated variables analyzed at the cluster level may be different from those at the original observation level (Kreft & De Leeuw, 1998). Wu (1995) indicates that multilevel models separate the estimated effects in the covariates into different levels, which can be interpreted as individual-level effects (i.e., within a cluster) and cluster-level effects (i.e., across clusters), respectively.
Intraclass Correlation
Intraclass correlation refers to correlation among observations within a cluster. The intraclass correlation coefficient (ICC) measures this degree of correlation. An ICC can be determined from an intercept-only model (i.e., a multilevel model with no covariates):
| (9) |
| (10) |
| (11) |
By combining equations 9 and 10, Equation 11, the intercept-only model, is produced. The intercept-only model does not account for any variance in the dependent variable. It only separates the variances of the dependent variable into two parts; that is, the variance of clusters, σu2, and the variance of observations at Level 1, σe2. The ICC, written as the symbol “ρ,” can be computed on the basis of these two variance components (Equation 12). ρ ranges from 0 to 1.
| (12) |
If all the observations are independent of one another, the ICC equals 0. At the other extreme, if all the responses from observations in all clusters are exactly the same, the ICC equals 1. A nonzero ICC implies that the observations are not independent. If observations are highly correlated, the variance of observations at Level 1, σe2, becomes smaller. In turn, the denominator in Equation 12 becomes smaller, which means that ICC becomes larger (Hox, 2002).
The ICC is interpreted in four ways. First, the ICC represents the degree of common environments that observations share. The ICC would increase if observations in the same cluster were under more similar environments and, as a result, if the responses of observations became more alike. The second interpretation of the ICC is the proportion of total variance (i.e., cluster plus individual variance) that is attributed to the cluster level, which is self-explanatory from Equation 12. Therefore, as the relative variance of the clusters increases, the less likely you are to assume that the groups are similar. The third interpretation of the ICC is the degree of homogeneity of Level 1 within Level 2 (i.e., the quantity of similarity among observations at the cluster level). If observations were not correlated, they would not affect one another nor would they be similar at all (i.e., no homogeneity). The last interpretation of the ICC is the anticipated correlation between two observations that are randomly chosen from the same cluster (e.g., correlation of two nurses within the same hospital) (Hox, 2002) Kreft & De Leeuw, 1998).
Choosing the Best Model
Several multilevel models can be tested (e.g., a two-level random intercept model and a two-level random coefficient model) depending on the researcher's purposes. The estimation of more than a two-level model is also possible, and there is no restriction regarding the number of random covariates (Hox, 2002; Kreft & De Leeuw, 1998). The choice of a relevant model is an important step, and it should be based on the necessity of parsimony in a model. Parsimony means that models should be as simple as possible (Hox, 2002).
The loglikelihoods of the two models are compared to select the model that best fits the data, if one model is a special case of the other model (Hox, 2002). Healy (2001) explains that the likelihood in a model is “the probability of the observed data if the estimated values of the parameters in the model were the true values” (p.7). The likelihood is transformed into the logarithm of the likelihood, because the logarithm of the likelihood function is more convenient to deal with in the process of parameter estimates, rather than the likelihood function (Allison, 1999b). The loglikelihood is not usually of interest in itself, but it plays a pivotal role in choosing one model between two alternative models (Healy, 2001).
To compare the fit of two models, calculate a χ2 statistic as the positive difference of 2× their respective loglikelihoods. The positive difference of 2×loglikelihood has a χ2 distribution with degrees of freedom obtained from the difference of the number of parameters to be estimated in the two models. If the statistic is not statistically significant, this suggests that a more complicated model may not be necessary (Hox, 2002). For instance, if a random intercept model and a random coefficient model are compared and if the χ2 statistic is not significant, this means that a random intercept model, which contains fewer parameters, is acceptable. The comparison of loglikelihoods can also be used to investigate the significance of a series of random coefficient variables in selecting a better model between a model that contains these random variables and a model that does not.
Empirical Example
Sample
The data were obtained from New Zealand hospital staff nurses in an extension to an international study that investigated the effects of both nurse staffing and nursing practice environments on hospital patient outcomes in five countries (Aiken, Clarke, & Sloane, 2002). The sample was 4,320 staff nurses in 19 acute general public hospitals in New Zealand. The number of nurses in each hospital ranged from 28 to 547. Nurses answered questions about their current job, burnout, and job satisfaction.
Model for Testing
A continuous dependent variable from a two-level structure was used to explore the random intercept model and the random coefficient model. The model for the analysis was:
Random Intercept Model:
| (13) |
Random Coefficient Model:
| (14) |
Equation 13 is the random intercept model and Equation 14 is the random coefficient model. In Equation 13, only the intercept β0j could be different across clusters and the slope β was considered as fixed, whereas in Equation 14, both the intercept β0j and slope βj could be different at the second level. Nurse burnout was used as the dependent variable and measured using nine items of “emotional exhaustion,” a subscale of the Maslach Burnout Inventory. Each item score ranged from 0 to 6. The nurses' burnout score was calculated as the sum of the nine item scores, and could vary from 0 to 54. A higher score of emotional exhaustion indicated that the amount of burnout was more intense (Maslach, Jackson, & Leiter, 1996). The average work hours per week in the past year was used as the covariate.
Software
For the analysis in this study, the software STATA with Generalized Linear Latent and Mixed Models (GLLAMMs) was used (Rabe-Hesketh, Pickles, & Skrondal, 2001). Also, the software SAS with PROC NLMIXED and the software HLM are available for the analysis of the multilevel models (Hox, 2002; Wolfinger, n.d.).
Results
For all respondents, the mean burnout score was 21.9 (SD = 11.2), which corresponds to an average level of burnout on the basis of published norms for a sample of nurses and physicians (Maslach et al., 1996). Across hospitals, the mean burnout score ranged from 16.5 (SD = 12.2) to 25.9 (SD = 12.0). The mean for work hours per week was 34.0, with an SD of 10.2. Across hospitals, the mean work hours per week varied from 30.2 (SD = 9.0) to 35.7 (SD = 11.2).
Underestimation of Standard Errors in the Conventional Linear Regression Model
As stated earlier, standard errors from clustered data may be underestimated in a conventional linear regression model (Hox, 2002). As expected, the standard errors in the conventional linear regression model were smaller than or equal to those in the random intercept model and the random coefficient model, although the difference of standard errors between these models was small (Table 1).
TABLE I.
Parameter Estimates and Standard Errors in a Conventional Linear Regression Model and Multilevel Models
| Conventional Linear Regression Model |
Intercept-only Model |
Random Intercept Model |
Random Coefficient Model |
|||||
|---|---|---|---|---|---|---|---|---|
| Predictor | Coefficient | SE | Coefficient | SE | Coefficient | SE | Coefficient | SE |
| Fixed part | ||||||||
| Intercept | 16.40** | 0.602 | 21.39** | 0.250 | 16.40** | 0.626 | 16.28** | 0.802 |
| Work hours | 0.17** | 0.017 | 0.15** | 0.017 | 0.16** | 0.022 | ||
| Random part | ||||||||
| σe2 | 121.46** | 2.655 | 118.78** | 2.636 | 118.53** | 2.637 | ||
| σu2 | 5.64** | 1.315 | 4.02* | 1.157 | 4.23 | 3.728 | ||
| σv2 | 0.002 | 0.002 | ||||||
| σuv2 | −0.071 | 0.087 | ||||||
| Loglikelihood | −15514.78 | −15513.64 | ||||||
Note. σe2: Variance at the nurse level; σu2: Variance of the intercept at the hospital level; σv2: Variance of the coefficient of work hours (i.e., the slope of work hours) at the hospital level; σuv2: Covariance between the intercept and the coefficient at the hospital level; S.E.: Standard Error.
p < .001.
p < .0001.
Random Intercept Model
The random intercept model treated only the intercept as a random component and estimated the variance of the intercept at the hospital level. The coefficients of the intercept (i.e., the degree of burnout when work hours are 0) and the covariate (i.e., the average effect of work hours on the degree of burnout) at the nurse level were also assessed. The intercept was 16.4, which stood for the average burnout score for all nurses in all hospitals, when work hours were 0. The coefficient estimate of work hours was 0.15, which implied that with a 1-hour increase of work per week, the average nurse's burnout score increased by 0.15. The intercept and the slope of work hours were statistically significant (p < .0001).
Unlike the conventional linear regression model that had the variance at the nurse level only, the random intercept model had two variances of the intercept: variance at the nurse level and variance at the hospital level. The nurse-level and hospital-level variances were separately estimated as 118.78 and 4.02, respectively. Even though the variance of the intercept at the hospital level was fairly small compared with the variance at the nurse level, the hospital-level variance of the intercept was statistically significant (p < .001). This result signified that the amount of burnout was significantly different across hospitals when the value of work hours was 0. The intercepts of the conventional linear regression model and the random intercept model were interpreted differently. The intercept of 16.4 as a fixed variable in the conventional regression implied that all nurses in all hospitals had the same burnout score when work hours were 0, and this score is considered unchanging. However, the intercept of 16.4 as a random variable in the random intercept model meant that although the mean intercept in all nurses across all hospitals was 16.4, the intercept could differ in particular hospitals. Based on the value of the intercept and the variance at the hospital level, the 95% predicted interval that contained the intercepts in the hospitals was calculated from the formula (Hox, 2002). The 95% predicted interval of the intercept (i.e., burnout score when work hours per week is 0) across hospitals was from 12.4 to 20.4 in this example.
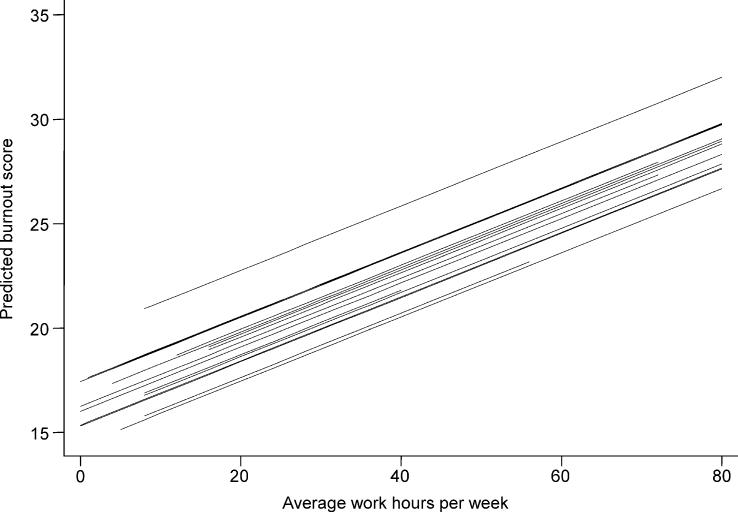
The existence of variance at the hospital level implied that the intercept could differ across hospitals. At the same time, the random intercept model did not allow the slope of work hours to vary across hospitals. Figure 1 illustrates the results of the random intercept model: the same slope of work hours, but different intercepts across hospitals. Each line represents the relationship between the average work hours per week and nurses' burnout in one hospital. All lines show that the number of work hours was positively associated with the amount of nurses' burnout, but the levels of burnout were not exactly the same when work hours were 0 (i.e., the intercept). The lines are parallel, which means that the slope, that is, the effect of the work hours on burn-out, is the same across hospitals.
FIGURE 1.
The random intercept model.
Random Coefficient Model
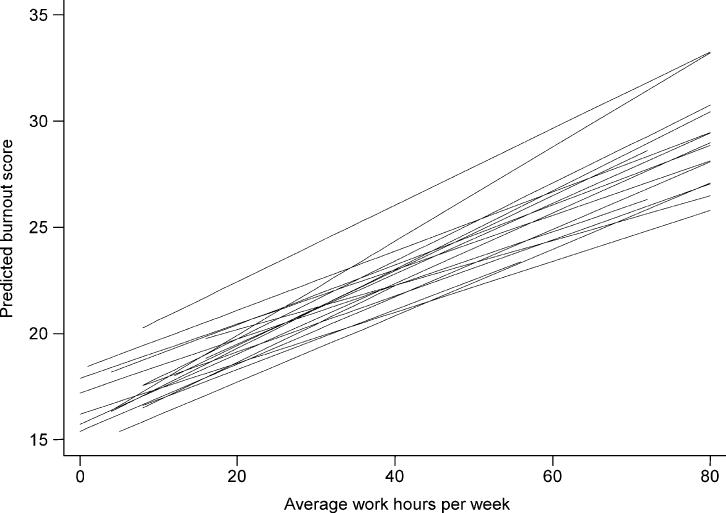
The parameter estimates of the intercept and the slope of work hours in the random coefficient model were almost the same as those in the random intercept model (Table 1). The difference between these models was that the random coefficient model allowed variability of the coefficient of the covariate at the hospital level (i.e., the effect of work hours on the degree of burnout at Level 2). The variability of work hours at the hospital level meant that the slope was no longer the same across hospitals. The variance of the slope of work hours at the hospital level was .002, and the covariance of the intercept and the slope was −0.071. This negative correlation would indicate that at the hospital level, higher values of baseline burnout (at theoretical zero for work hours) would be associated with a relatively smaller effect of work hours on burnout. However, the hospital-level random effects (i.e., the variability of the intercept and the slope of work hours and the covariance between them at the hospital level) were not statistically significant. This finding implied that the slope of work hours across hospitals did not differ notably. Figure 2 illustrates the results of the random coefficient model. Here, the slopes of the lines, representing the effect of work hours on burnout in each hospital, are not parallel and the intercepts differ across hospitals.
FIGURE 2.
The random coefficient model.
Intraclass Correlation and Likelihood Ratio Test
The intraclass correlation was calculated from the results of the interceptonly model in Table 1. The interceptonly model had no covariates. Hence, this model divided the variance of burnout into two components: nurse level and hospital level (Hox, 2002). The intraclass correlation based on these two variance components (see Equation 12) was 5.64/(121.46 + 5.64) = .044. Thus, the variance at the hospital level accounted for 4.4% of the total variance of burnout.
The likelihood ratio test was conducted to see whether the random intercept model or the random coefficient model better fit the data. The positive difference of 2× loglikelihood, 2.28, in two models followed a χ2 distribution with one degree of freedom. The p value of the test statistic was .13, which demonstrated that the simpler model, the random intercept model, fit the data better. This result also indicated that the different slopes of work hours across hospitals could be eliminated from the model.
Discussion
In this presentation, a model with one covariate was introduced to illustrate and to compare the results of the random intercept model versus the random coefficient model. The multilevel models demonstrated the correction of the underestimated standard errors in the conventional linear regression model. Standard errors in the conventional regression were not substantially underestimated, however, which happens when observations within clusters are not highly correlated. The small ICC of .044 in the example demonstrates the low degree of correlation among observations within a cluster. The comparison of the loglikelihood between the two models showed that the simpler model, the random intercept model, was more appropriate.
Although the ICC was quite low in the empirical example, it was consistent with existing literature. In a review of organizational research literature, James (1982) reported a median ICC of .12 for measures of organizational climate. A lower ICC for nurse burnout as compared with that for organizational climate would seem reasonable. Greater perceptual agreement would be expected within organizations about an organizational phenomenon such as climate than about an individual outcome such as burnout. Indeed, in a study of 632 nurses on 54 nursing units in four hospitals, Forbes and Taunton (1994) reported a substantially lower ICC of .003 at the hospital level and .04 at the nursing unit level for a different job outcome, job enjoyment. That study demonstrated hospital-level ICCs of .03 to .07 and nursing unit ICCs of .03 to .23 for three organizational phenomena: nurse manager structuring expectations, nurse manager consideration, and control over practice. These hospital versus nursing unit differences in the ICC reflect greater perceptual agreement at the workgroup level than at the institutional level. Data analyzed by Hughes and Anderson (1994) from 223 registered nurses, licensed vocational nurses, and nurses aides on a skilled nursing unit in each of 14 nursing homes yielded ICCs of .03 and .02, respectively, for two organizational phenomena: decentralization and participation in decision making. Thus, ICCs for both organizational and individual phenomena appear from the literature to be low in general.
When observations are more highly correlated, the difference of standard errors between the conventional regression model and the multilevel models becomes greater. In the empirical example, there was a minimal difference of standard errors between conventional and multilevel models, consistent with the low ICC. Moreover, the substantive findings (i.e., the effect of work hours on burnout) did not differ between models. In instances where the ICC is low, the use of methods that seek to address the underestimated error term may not be necessary.
The application of multilevel models for clustered data has attractive features: (a) the correction of underestimation of standard errors, (b) the examination of the cross-level interaction, (c) the elimination of concerns about aggregation bias, and (d) the estimation of the variability of coefficients at the cluster level. Moreover, it is feasible to choose the better model through the likelihood ratio test and to estimate the amount of intraclass correlation (Kreft & De Leeuw, 1998; Teachman & Crowder, 2002; Wu, 1995).
Even if multilevel models have the above strengths, they should be used only after prudent consideration of the following factors. First, the process of maximum likelihood, which determines parameter estimates in multilevel models, is computationally intense because iterations continue until the best parameters are determined (Hox, 2002). As the number of parameters to be estimated increases, it takes longer to obtain those estimates. This means that the random coefficient model is more computationally intense than the random intercept model (Wong & Mason, 1985). Second, when more parameters are estimated using the available data, precision might be lost because to estimate additional parameters, new assumptions regarding those parameters are needed (Raudenbush & Sampson, 1999). These two factors suggest how important it is to choose a parsimonious model for testing to yield efficiency and precision.
It is essential to take into account the contexts in which observations are collected because of the possibility of correlated responses among observations. Multilevel models can yield reliable results by reflecting a hierarchical structure, thereby correcting the underestimation of standard errors. These models can also unveil the importance of the hierarchical structure in the relationships between factors of interest. Therefore, the application of multilevel models should be considered in the analysis of clustered data.
Footnotes
This research was supported by a grant from the National Institute of Nursing Research (NR004513). The principal investigator is Linda H. Aiken, PhD, RN, FAAN, FRCN, Director of the Center for Health Outcomes and Policy Research at the University of Pennsylvania.
Contributor Information
Sunhee Park, a doctoral student, School of Nursing, University of Pennsylvania, Philadelphia..
Eileen T. Lake, Assistant Professor, School of Nursing, Secondary Faculty, Department of Sociology, University of Pennsylvania, Philadelphia..
References
- Aiken LH, Clarke SP, Sloane DM. Hospital staffing, organization, and quality of care: Cross-national findings. International Journal for Quality in Health Care. 2002;14(1):5–13. doi: 10.1093/intqhc/14.1.5. [DOI] [PubMed] [Google Scholar]
- Allison PD. Multiple regression: A primer. Pine Forge Press; Thousand Oaks, CA: 1999a. [Google Scholar]
- Allison PD. Logistic regression using the SAS system: Theory and application. SAS Institute; Cary, NC: 1999b. [Google Scholar]
- Cho SH. Using multilevel analysis in patient and organizational outcomes research. Nursing Research. 2003;52(1):61–65. doi: 10.1097/00006199-200301000-00010. [DOI] [PubMed] [Google Scholar]
- Cho SH, Ketefian S, Barkauskas VH, Smith DG. The effects of nurse staffing on adverse events, morbidity, mortality, and medical costs. Nursing Research. 2003;52(2):71–79. doi: 10.1097/00006199-200303000-00003. [DOI] [PubMed] [Google Scholar]
- Forbes S, Taunton RL. Reliability of aggregated organizational data: An evaluation of five empirical indices. Journal of Nursing Measurement. 1994;2(1):37–48. [PubMed] [Google Scholar]
- Guo G, Zhao H. Multilevel modeling for binary data. Annual Review of Sociology. 2000;26:441–462. [Google Scholar]
- Healy M. Multilevel data and their analysis. In: Leyland AH, Goldstein H, editors. Multilevel modeling of health statistics. Wiley; West Sussex: 2001. pp. 1–12. [Google Scholar]
- Hox J. Multilevel analysis: Techniques and applications. Lawrence Erlbaum; Mahwah, NJ: 2002. [Google Scholar]
- Hox JJ, Kreft IG. Multilevel analysis methods. Sociological Methods & Research. 1994;22(3):283–299. [Google Scholar]
- Hughes LC, Anderson RA. Issues regarding aggregation of data in nursing systems research. Journal of Nursing Measurement. 1994;2(1):79–101. [PubMed] [Google Scholar]
- James LR. Aggregation bias in estimates of perceptual agreement. Journal of Applied Psychology. 1982;67:219–229. [Google Scholar]
- Kreft I, De Leeuw J. Introducing multilevel modeling. Sage; Thousand Oaks, CA: 1998. [Google Scholar]
- Mark BA, Salyer J, Wan TT. Market, hospital, and nursing unit characteristics as predictors of nursing unit skill mix: A contextual analysis. Journal of Nursing Administration. 2000;30(11):552–560. doi: 10.1097/00005110-200011000-00011. [DOI] [PubMed] [Google Scholar]
- Mark BA, Salyer J, Wan TTH. Professional nursing practice: Impact on organizational and patient outcomes. Journal of Nursing Administration. 2003;33(4):224–234. doi: 10.1097/00005110-200304000-00008. [DOI] [PubMed] [Google Scholar]
- Mark BA, Harless DW, McCue M, Xu Y. A longitudinal examination of hospital registered nurse staffing and qualify of care. Health Services Research. 2004;39(2):279–300. doi: 10.1111/j.1475-6773.2004.00228.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maslach C, Jackson SE, Leiter MP. Maslach burnout inventory manual. 3rd Consulting Psychologists Press; Palo Alto, CA: 1996. [Google Scholar]
- McGillis Hall LM, Doran D, Baker GR, Pink GH, Sidani S, O'Brien-Pallas L, et al. Nurse staffing models as predictors of patient outcomes. Medical Care. 2003;41(9):1096–1109. doi: 10.1097/01.MLR.0000084180.07121.2B. [DOI] [PubMed] [Google Scholar]
- Moore DS, McCabe GP. Introduction to the practice of statistics. 4th Freeman & Co; New York: 2003. [Google Scholar]
- Rabe-Hesketh S, Pickles A, Skrondal A. http://www.gllamm.org/manual.pdf. GLLAMM manual: Technical report 2001/01. 2001 Retrieved December 27, 2003.
- Raudenbush SW, Bryk AS. Hierarchical linear models: Applications and data analysis methods. 2nd Sage; Thousand Oaks, CA: 2002. [Google Scholar]
- Raudenbush SW, Sampson RJ. Assessing direct and indirect effects in multilevel designs with latent variables. Sociological Methods. 1999;28(2):123–153. [Google Scholar]
- Reise SP, Duan N. Multilevel modeling and its application in counseling psychology research. The Counseling Psychologist. 1999;27(4):528–551. [Google Scholar]
- Teachman J, Crowder K. Multilevel models in family research: some conceptual and methodological issues. Journal of Marriage and Family. 2002;64:280–294. [Google Scholar]
- Wolfinger RD. http://support.sas.com/rnd/app/papers/nlmixedsugi.pdf. Fitting nonlinear mixed models with the new NLMIXED procedure. (n.d.) Retrieved October 10, 2004.
- Wong GY, Mason WM. The hierarchical logistic regression model for multilevel analysis. Journal of the American Statistical Association. 1985;80(391):513–524. [Google Scholar]
- Wu YW. Hierarchical linear models: A multilevel data analysis technique. Nursing Research. 1995;44(2):123–126. doi: 10.1097/00006199-199503000-00012. [DOI] [PubMed] [Google Scholar]