Abstract
Background. Muscles which cause glenohumeral external rotation possess varying ability for generating force and moment due to differences in muscle architecture, moment arm, and the interaction of these two factors. This study’s purpose was to determine a complete dataset of muscle-tendon parameters for predicting the moment generating capacity and force-length dependence for external rotation of infraspinatus, supraspinatus and teres minor muscles.
Methods. Muscle fascicle length, sarcomere length, pennation angle, and muscle volume were measured for sub-regions of infraspinatus and supraspinatus, and teres minor from 10 glenohumeral specimens. Tendon excursion was measured for glenohumeral rotation. From these parameter measurements, optimal fascicle length, physiological cross-sectional area, muscle force-length dependence, and maximum isometric moment generating capacity were calculated.
Findings. Substantial differences were found for optimal muscle length, physiologic cross-sectional area, and tendon length for the 10 specimens of this study. Muscle sub-region had a significant effect on the force-length relationship for infraspinatus (P < 0.001), but was not significant for supraspinatus (P = 0.49). For infraspinatus and supraspinatus, maximum isometric rotation moment capacity was greater at 10° versus 60° abduction (P < 0.001). Maximum isometric rotation moment capacity for the teres minor was greater at 10° versus 60° abduction (P < 0.01). Sub-regions demonstrated significant differences in isometric moment capacity (P < 0.001).
Interpretation. Functional capabilities of these muscles depend on muscle architecture and moment arm as well as their combined effects. The results allow for development of stochastic and deterministic models of glenohumeral external rotation strength which can be used for prediction of muscle forces and joint moments.
Keywords: Shoulder, External rotation, Muscle architecture
1. Introduction
Measurements which allow one to understand and model muscle force and moment generating capacity can be made directly on a muscle and the joint which it moves. Muscle physiological cross-sectional area (PCSA) is a relative description of maximum muscle force generating capacity. Similarly, optimal muscle length, muscle belly and fascicle lengths, and muscle-tendon excursion relative to joint angle determine a muscle’s force-length relationship.
Previous authors have measured muscle architecture (Amis et al., 1979; Bassett et al., 1990; Veeger et al., 1991, 1997) and moment arms (Otis et al., 1994; Kuechle et al., 1997, 2000; Hughes et al., 1998) at the shoulder. Due to parameter variability and covariance, it is advantageous to measure parameters in conjunction with one another, rather than to use parameters from different data-sets (Hoffer et al., 1989; Hoy et al., 1990; Loren et al., 1996). In addition, stochastic musculoskeletal models (Hughes and An, 1997; McLean et al., 2003; Valero-Cuevas et al., 2003; Davidson et al., 2004) require parameter distributions. Measuring all parameters on the same specimens will allow for determination of parameter covariance. However, only two studies conducted at the wrist (Loren et al., 1996), and at the elbow (Murray et al., 2000), have measured all parameters on the same specimens.
The hypothesis for this study was that glenohumeral external rotation muscles possess varying capacities to generate force and moment due to differences in muscle architecture, moment arm, and the interaction of these two factors. The purpose of this study was to determine a complete dataset of muscle-tendon parameters suitable for predicting the force generating capacity of sub-regions of infraspinatus, supraspinatus and teres minor muscles. Combining the information attained here with measured moment arms allows for determination of the moment generating capacity of these muscles.
2. Methods
Data required for describing the force generating capacity of supraspinatus, infraspinatus and teres minor were collected from 10 fresh frozen human cadaver humerusscapula extremities obtained from anatomical donations (Table 1). Moment arm data were also measured from the same specimens (Langenderfer et al., 2005).
Table 1.
Cadaver anthropometric parameters
| Specimen (gender) | Height (m) | Weight (kg) | Scapula length (AC-AI) (cm) | Humerus length (cm) |
|---|---|---|---|---|
| 1 (F) | 1.68 | 50.0 | 17.0 | 31.1 |
| 2 (F) | 1.63 | 61.4 | 15.6 | 27.4 |
| 3 (M) | 1.78 | 58.6 | 17.6 | 29.7 |
| 4 (M) | 1.75 | 97.7 | 21.7 | 35.8 |
| 5 (M) | 1.73 | 60.9 | 20.2 | 37.1 |
| 6 (M) | 1.96 | 122.7 | 20.7 | 36.7 |
| 7 (M) | 1.88 | 118.2 | 19.8 | 33.5 |
| 8 (M) | 1.57 | 100.0 | 20.5 | 36.4 |
| 9 (M) | 1.75 | 109.1 | 19.7 | 32.7 |
| 10 (F) | 1.68 | 77.3 | 18.6 | 30.9 |
The specimens were frozen at -20 °C for a period of approximately 2 weeks. Twenty-four hours prior to dissection specimens were thawed in a room temperature water bath. Specimens were prepared by blunt dissection of all muscles and tissue superficial to the rotator cuff. The entirety of infraspinatus, teres minor and supraspinatus were carefully elevated from origins and placed flat on a table. Tendon width at the musculotendinous junction, and muscle belly width at the widest point of supraspinatus and infraspinatus, was measured with a digital caliper. Tendon and muscle were then dissected into three and four equal width portions for the supraspinatus and infraspinatus, respectively. The teres minor was dissected as one unit. Each muscle sub-region was treated as an individual muscle for purposes of parameter measurement. Tendon length was measured with digital calipers as the distance from the insertion on the humeral head to the most distal location of muscle fascicles. Tendon thickness at the musculotendinous junction was also measured with calipers.
Parameter measurements were sequentially taken from each muscle-tendon unit immediately following dissection. Saline was used to prevent muscle dehydration during the protocol. Following dissection, supraspinatus and teres minor were manipulated into parallelepipedon shapes (An et al., 1981; Brand et al., 1981) for measurement of muscle belly length, muscle fascicle length, and pennation angle. The infraspinatus is of irregular shape, and therefore was positioned in a manner consistent with anatomy in order to make these measurements. Muscle belly length, and muscle fascicle length were measured with a digital caliper to the nearest millimeter. Muscle volume was measured via water immersion. Pennation angle was measured with a goniometer to the nearest degree. Muscles were placed in a solution of 20% neutral buffered formalin for 1 week for fixation.
After fixation, fascicles were dissected from the muscle interior, below the outer fascicle layer, using fine sharp dissection. Muscles were divided into proximal, middle and distal regions, and three fascicles were dissected from each region, respectively. This division ensured fascicles were obtained from all portions of the muscle. Fascicles were mounted on slides with Kaiser’s jelly and coverslipped. A custom built diffractometer was used to measure sarcomere lengths (Lieber et al., 1990; Murray et al., 2000; Delp et al., 2001). The wavelength, k, of the 5 mW helium-neon laser was 632.8 nm.
The width of the first order diffraction band was measured and the sarcomere length, lS, was calculated.
| (1) |
where L is the distance from the fascicle to the diffraction band, and y is the width of the first order band.
Five sarcomere measurements were taken from each fascicle for a total of 45 sarcomere lengths per muscle or muscle sub-region. This number of measurements was sufficient to achieve 80% power of detecting the mean sarcomere length (Langenderfer et al., 2004). In rare circumstances, 10 of 720 muscle fascicles, no diffraction pattern was observable. The fascicles which did not yield a diffraction pattern were only once present in the same muscle, and so the ability to measure mean sarcomere length for a given muscle was not appreciably affected.
Because diffraction pattern measurement is a subjective process, a pilot study was conducted to assess the interrater reliability (Portney and Watkins, 1993) of multiple raters measuring the same sarcomere diffraction pattern. All raters involved in the study independently measured the diffraction pattern of 20 muscle fascicles. The intraclass correlation for four raters measuring the same sarcomere length diffraction patterns was 0.99. All other measurements (muscle belly length, fascicle length, tendon length, and muscle volume) were performed by one rater.
Optimal fascicle lengths, lfo,were determined by normalizing the measured fascicle length, lf, by the ratio of optimal sarcomere length (2.8 lm) (Walker and Schrodt, 1974) to the mean measured sarcomere length
| (2) |
Optimal muscle length was estimated as measured muscle length normalized to an optimal sarcomere length of 2.8 lm. Muscle PCSA was determined as muscle volume divided by optimal fascicle length. Tendon cross-sectional area was determined as tendon width multiplied by tendon thickness.
To determine how muscle architecture and moment arm influence muscle function, the force-length relationship and maximum isometric moment generating capacity for each muscle sub-region was estimated (Loren et al., 1996; Murray et al., 2000). Force-length relationships were estimated for each muscle sub-region of each specimen for glenohumeral rotation for the position of 10° abduction. Tendon excursion as a function of joint angle was measured from 45° internal to 45° external rotation (Langenderfer et al., 2005)at10° and 60° abduction on the same 10 specimens. Neutral rotation was defined by aligning the rod aligned with the humeral epicondyles with the scapular plane. Inelastic tendon was assumed, and fascicle excursion as a function of joint angle, lf(θ) was calculated from tendon excursion, etθ, and pennation angle, a (Eq. (3)), where lf(0) and et(0) represent fascicle length and tendon excursion at neutral rotation, respectively.
| (3) |
Rigor was assumed to develop with the humerus in neutral rotation and 10° abduction. Consequently, the above equation yields the fascicle length measured on dissected muscles at the position of 10° external rotation. Muscle fascicle length then was normalized by the optimal muscle fascicle length determined via sarcomere measurements. Normalized muscle forces were calculated from normalized muscle fascicle lengths (Zajac, 1989).
Maximum isometric rotation moment capacity was estimated as the product of PCSA, the cosine of the pennation angle, and the maximum rotation moment arm at each of two positions, 10° abduction, and 60° abduction in the scapular plane. Maximum rotation moment arms were determined from the tendon excursion data described earlier. In this manner, maximum isometric rotation moment capacity is independent of muscle stress and has units of length cubed.
Independent one-way analysis of variance (ANOVA) models were used for each muscle, supraspinatus and infraspinatus, to determine if the muscle sub-regions were operating on different portions of the force-length relationship. Specifically, normalized fascicle length was determined at 15° increments from 45° internal to 45° external rotation for each sub-region of each specimen at 10° abduction. Two-way ANOVA models were used to test for the effect of abduction angle (10° and 60°), and muscle sub-region (four and three sub-regions, respectively) on maximum moment capacity of infraspinatus and supraspinatus. For teres minor a one-way ANOVA model was used to test for the effect of abduction angle on maximum moment capacity. In each case, specimen was a blocking variable to account for interspecimen variability. Statistical analysis was conducted with SYSTAT 10.2.
3. Results
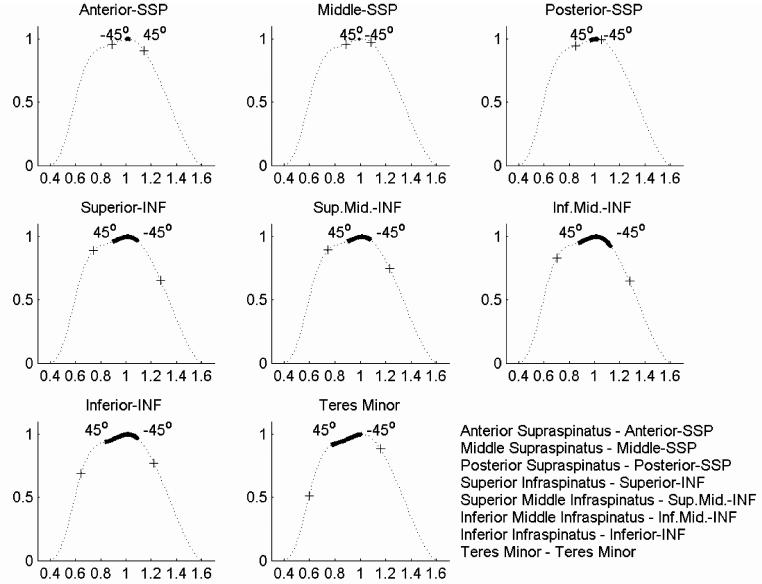
The muscles studied here demonstrated substantial differences in optimal muscle length, PCSA, and tendon length across the 10 specimens of this study (Table 2). The estimated force-length relationships for the eight muscle sub-regions were determined for the range of 45° internal to 45° external rotation with the humerus at 10° abduction relative to the scapula (Fig. 1). The supraspinatus operated through a smaller portion of its force-length relationship than infraspinatus or teres minor. The effect of muscle sub-region on the force-length relationship was significant for infraspinatus (P < 0.001), but was not significant for supraspinatus (P = 0.49).
Table 2.
Summarized muscletendon architecture parameters
| Tendon length (mm) | Tendon area (cm2) | PCSA (cm2) | Pennation angle (deg) (cm) | Muscle length (cm) | Fascicle length (cm) | Mean sarcomere length (μm) | Optimal fascicle length (cm) | Optimal muscle length (cm) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Anterior-SSP | 39.5 | (13.5) | 0.404 | (0.090) | 1.36 | (0.40) | 10 | (4.3) | 10.6 | (1.6) | 7.8 | (1.5) | 2.91 | (0.31) | 7.5 | (1.5) | 10.3 | (2.1) |
| Middle-SSP | 33.4 | (12.7) | 0.392 | (0.118) | 1.27 | (0.34) | 12 | (6.4) | 12.4 | (2.1) | 8.7 | (1.6) | 2.91 | (0.31) | 8.4 | (1.5) | 12.0 | (2.0) |
| Posterior-SSP | 30.4 | (9.7) | 0.344 | (0.073) | 0.97 | (0.40) | 11 | (3.5) | 11.8 | (1.8) | 8.7 | (1.3) | 2.95 | (0.29) | 8.3 | (1.3) | 11.2 | (1.9) |
| Superior-INF | 41.5 | (14.6) | 0.320 | (0.121) | 1.83 | (0.66) | 17 | (3.7) | 13.2 | (1.7) | 8.8 | (2.3) | 3.02 | (0.38) | 8.1 | (1.7) | 12.3 | (1.6) |
| Sup.Mid.-INF | 41.8 | (16.9) | 0.324 | (0.118) | 1.80 | (0.73) | 15 | (5.6) | 14.8 | (2.0) | 9.2 | (2.6) | 3.07 | (0.36) | 8.3 | (1.8) | 13.5 | (1.6) |
| Inf.Mid.-INF | 38.7 | (18.0) | 0.273 | (0.112) | 2.08 | (0.92) | 18 | (7.2) | 16.0 | (2.4) | 10.4 | (3.1) | 3.02 | (0.34) | 9.5 | (2.5) | 14.9 | (1.9) |
| Inferior-INF | 25.5 | (9.7) | 0.244 | (0.053) | 1.47 | (0.51) | 19 | (5.7) | 16.7 | (2.6) | 10.0 | (2.9) | 2.91 | (0.39) | 9.5 | (2.6) | 16.2 | (2.7) |
| Teres minor | 22.7 | (12.2) | 0.447 | (0.301) | 2.02 | (0.80) | 11 | (7.7) | 11.4 | (1.4) | 8.1 | (2.0) | 2.66 | (0.39) | 8.4 | (1.9) | 12.0 | (1.4) |
Mean (standard deviation).
Fig. 1.
Estimated operating ranges of the muscles measured in this study from -45° (internal) to 45° (external) rotation. Fascicle excursions calculated from tendon excursion and pennation angle were normalized by optimal sarcomere length calculated from measured sarcomere lengths and superimposed on the normalized force-length curves. The solid dark line is the mean length-tension dependence across the 10 specimens, (+) represents one standard deviation each direction.
Maximum moment generating capacity demonstrated variability across muscle sub-regions and between specimens (Fig. 2). Differences in maximum moment generating capacity reported for the 10° versus 60° abduction positions reflect differences in the moment arms only, and not differences in muscle force between these positions. For infraspinatus, maximum isometric rotation moment capacity was greater at 10° (mean: 4.40, SD 0.28 cm3) versus 60° abduction (mean 2.83, SD 0.28 cm3) (P < 0.001). Muscle sub-region had a significant effect (P < 0.001) on maximum isometric external rotation moment capacity of infraspinatus. Maximum moment capacity increased from superior (mean 3.37, SD 0.41 cm3), to superior-middle (mean 3.66, SD 0.41 cm3), to inferior-middle (mean 4.42, SD 0.41 cm3) infraspinatus sub-region, and then decreased for the inferior sub-region (mean 3.01, SD 0.41 cm3) (Fig. 2). Maximum isometric rotation moment capacity for the teres minor was significantly different (P < 0.01) at 10° (mean 4.71, SD 0.28 cm3) versus 60° abduction (mean 5.09, SD 0.28 cm3). For supraspinatus, muscle sub-region had a significant effect (P < 0.01) on maximum isometric external rotation moment capacity. Moment capacity was greatest for the middle sub-region (mean 1.53, SD 0.28 cm3) of supraspinatus as opposed to anterior (mean 1.12, SD 0.28 cm3) and posterior (mean 1.18, SD 0.28 cm3) sub-regions (Fig. 2). The moment capacity for sub-regions of supraspinatus at 10° abduction (1.65 ± 0.08 cm3) was greater than at 60° (mean 0.90, SD 0.28 cm3) (P < 0.001) (Fig. 2).
Fig. 2.
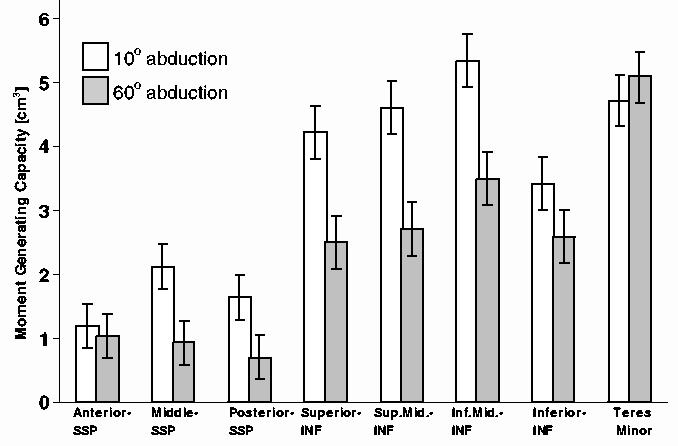
Maximum isometric rotation moment generating capacity (standard error) for sub-regions of infraspinatus, estimated as the product of PCSA, maximum moment arm, and cosine of pennation angle, at 10° and 60° abduction.
On average optimal fascicle length and optimal muscle length of infraspinatus increased from superior to superior-middle, to inferior-middle, to inferior regions (Table 2). Average optimal fascicle lengths were longer for the middle regions of supraspinatus (mean 8.4, SD 1.5 cm) as opposed to the anterior (mean 7.5, SD 1.5 cm) and posterior regions (mean 8.3, SD 1.3 cm2). PCSA of supraspinatus decreased on average from the anterior (mean 1.36, SD 0.40 cm2), to middle (mean 1.27, SD 0.34 cm2), to posterior regions (mean 0.97, SD 0.40 cm2).
4. Discussion
This study generated data for describing the muscle force and moment generating capacity of glenohumeral external rotators. These parameters can be used to develop computational models of the musculature crossing the glenohumeral joint. Additionally, the muscle force-length dependence and the moment generating ability of the muscles has been described. Substantial interspecimen variability exists in these relationships. The results emphasize that a description of the means by which a muscle actuates the musculoskeletal system requires a complete understanding of muscle moment arm, optimal fascicle length, muscle fascicle excursion as a function of joint angle and muscle PCSA.
This study is the first documentation of the force-length dependence in conjunction with moment generating capacity for the muscles considered here. The force-length relationships are not perfect, but are a step towards answering one of the most pressing current challenges of musculoskeletal modeling. In the future it would be interesting to compare the results determined here to in vivo measurements as have been described for other joints and muscles (Lieber et al., 1994; Lieber and Friden, 1997). A limitation is that we were only able to determine the relationships for the position of 10° abduction and not for the 60° abducted position. This limitation results from assumptions for estimating muscle length as a function of joint angle, and technical limitations for estimating and comparing tendon excursions for multiple abduction positions using the tendon excursion method. The assumptions in the determination of these relationships are that average sarcomere length is representative of all sarcomeres in a given sub-region, muscle fascicles measured on the freshly harvested muscles are for the position of 10° abduction and neutral rotation, and tendons were perfectly inelastic. Such assumptions are not perfect, but were necessary given the limitations of this study. The results obtained are a step towards understanding the interaction between muscletendon properties and moment arms on shoulder external rotation strength.
Like other studies (Murray et al., 2000), we found substantial variability in sarcomere lengths of the muscles measured here. Representing these sarcomere lengths by their mean value does not capture this variability; however, we divided the muscles into sub-regions in order to determine differences in force and moment generating capacity across the muscle width. However, sarcomere lengths did not vary substantially across sub-regions (Table 2). Rather, there was a given spread in sarcomere lengths (0.3-0.4 lm) with no systematic difference in sarcomere length across sub-regions.
We did not know the exact joint position at which subjects deceased. We harvested specimens from anatomical donations and the specimens were frozen, but specimens were not always perfectly at neutral rotation and 10° abduction. We did not measure fascicle or muscle lengths in situ, but rather made such measurements on muscles which were dissected from the specimens. For this reason lengths might not exactly correspond to the exact shoulder position of 10° abduction and neutral rotation. Consequently, the variability of length-tension relationships are likely larger than would be determined from an in vivo technique.
To determine fascicle excursions from tendon excursions we assumed that tendons were inelastic. Tendon elasticity results in maximum tendon strain of 3.3% (Zajac, 1989), and 1.99-3.68% (Loren and Lieber, 1995) at maximum isometric muscle force. The discrepancy in muscle strain has been found to be less than 3% when tendon was modeled as elastic versus inelastic. (Chang et al., 1999). For the muscles considered here which are operating near the peak of the length-tension relationship, a nominal muscle strain discrepancy of 3% introduces an error of less than 5% for muscle force. We believe this study provides reasonable approximations of fascicle length changes, and length-tension dependence during shoulder external rotation.
Another shortcoming of this study is that tendon width and thickness were measured with calipers, which is a contact based method. Non-contact methods provide a better measurement of these parameters (Woo et al., 1990; McGough et al., 1996). Another method for measuring tendon cross-sectional areas is volume immersion (Loren and Lieber, 1995; Langenderfer et al., 2004). However, tendon could not be transected and measured via immersion because the moment arm measurement technique required intact tendons.
In this study the force-length properties and the maximum isometric moment generating capacity of infraspinatus, supraspinatus, teres minor were determined. This study is the first attempt to describe the force-length dependence of these muscles. The data presented here allow for determination of more descriptive muscle representations. Deterministic and probabilistic models of shoulder external rotation strength which predict muscle forces for infraspinatus, teres minor and supraspinatus can be developed from the data presented here.
Table A.1.
Tendon length (mm) for each muscle sub-region and each specimen
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Anterior-SSP | 37 | 31 | 42 | 52 | 46 | 64 | 45 | 17 | 36 | 25 |
| Middle-SSP | 35 | 29 | 34 | 55 | 36 | 47 | 41 | 12 | 26 | 19 |
| Posterior-SSP | 30 | 31 | 33 | 46 | 41 | 32 | 35 | 14 | 24 | 18 |
| Superior-INF | 29 | 32 | 53 | 68 | 54 | 37 | 52 | 37 | 33 | 20 |
| Sup.Mid.-INF | 28 | 28 | 60 | 72 | 47 | 45 | 56 | 33 | 29 | 20 |
| Inf.Mid.-INF | 25 | 22 | 57 | 57 | 33 | 64 | 58 | 30 | 22 | 19 |
| Inferior-INF | 12 | 18 | 42 | 39 | 24 | 30 | 30 | 23 | 19 | 18 |
| Teres minor | 8 | 0 | 28 | 36 | 34 | 33 | 32 | 20 | 14 | 22 |
Table A.2.
Tendon area (cm2) for each muscle sub-region and each specimen
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Anterior-SSP | 0.28 | 0.36 | 0.28 | 0.52 | 0.45 | 0.45 | 0.55 | 0.40 | 0.40 | 0.36 |
| Middle-SSP | 0.33 | 0.54 | 0.21 | 0.52 | 0.36 | 0.57 | 0.44 | 0.30 | 0.30 | 0.36 |
| Posterior-SSP | 0.37 | 0.45 | 0.21 | 0.31 | 0.36 | 0.45 | 0.33 | 0.30 | 0.30 | 0.36 |
| Superior-INF | 0.09 | 0.56 | 0.30 | 0.35 | 0.35 | 0.24 | 0.40 | 0.35 | 0.32 | 0.24 |
| Sup.Mid.-INF | 0.13 | 0.56 | 0.30 | 0.28 | 0.35 | 0.24 | 0.40 | 0.42 | 0.32 | 0.24 |
| Inf.Mid.-INF | 0.14 | 0.48 | 0.20 | 0.28 | 0.35 | 0.12 | 0.40 | 0.28 | 0.24 | 0.24 |
| Inferior-INF | 0.14 | 0.32 | 0.20 | 0.21 | 0.28 | 0.24 | 0.30 | 0.28 | 0.24 | 0.23 |
| Teres minor | 0.31 | 0.00 | 0.24 | 0.40 | 0.32 | 0.75 | 0.90 | 0.88 | 0.22 | 0.45 |
Table A.3.
PCSA (cm2) for each muscle sub-region and each specimen
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Anterior-SSP | 1.09 | 1.51 | 1.36 | 1.44 | 1.23 | 2.28 | 1.39 | 1.32 | 0.68 | 1.30 |
| Middle-SSP | 1.02 | 1.37 | 0.79 | 1.21 | 1.37 | 1.86 | 1.62 | 1.50 | 0.81 | 1.16 |
| Posterior-SSP | 0.86 | 0.71 | 0.33 | 1.20 | 1.26 | 0.97 | 1.74 | 1.23 | 0.58 | 0.86 |
| Superior-INF | 0.88 | 2.03 | 1.18 | 1.78 | 1.73 | 2.14 | 3.15 | 2.46 | 1.24 | 1.72 |
| Sup.Mid.-INF | 1.24 | 1.48 | 1.15 | 1.37 | 2.09 | 1.91 | 3.49 | 2.44 | 1.19 | 1.62 |
| Inf.Mid.-INF | 1.31 | 1.94 | 1.44 | 2.02 | 1.63 | 2.16 | 4.25 | 3.04 | 1.24 | 1.78 |
| Inferior-INF | 0.72 | 1.76 | 1.15 | 1.64 | 1.01 | 1.26 | 2.00 | 2.47 | 1.42 | 1.29 |
| Teres minor | 1.40 | 1.85 | 0.84 | 2.01 | 1.95 | 2.81 | 3.08 | 3.31 | 1.43 | 1.55 |
Table A.4.
Pennation angle (deg) for each muscle sub-region and each specimen
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Anterior-SSP | 10 | 10 | 14 | 5 | 0 | 10 | 12 | 10 | 15 | 10 |
| Middle-SSP | 5 | 5 | 12 | 5 | 15 | 20 | 10 | 24 | 11 | 12 |
| Posterior-SSP | 5 | 5 | 11 | 14 | 14 | 10 | 14 | 14 | 10 | 10 |
| Superior-INF | 14 | 16 | 15 | 15 | 19 | 15 | 23 | 13 | 23 | 14 |
| Sup.Mid.-INF | 10 | 16 | 14 | 10 | 28 | 12 | 10 | 15 | 20 | 15 |
| Inf.Mid.-INF | 28 | 12 | 5 | 12 | 19 | 27 | 14 | 23 | 17 | 18 |
| Inferior-INF | 26 | 15 | 19 | 26 | 24 | 15 | 25 | 10 | 16 | 16 |
| Teres minor | 19 | 19 | 5 | 22 | 0 | 0 | 12 | 10 | 12 | 14 |
Table A.5.
Muscle length (cm) for each muscle sub-region and each specimen
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Anterior-SSP | 10.1 | 9.3 | 8.1 | 11.8 | 11.4 | 12.3 | 10.1 | 12.9 | 11.7 | 9.2 |
| Middle-SSP | 1.8 | 8.8 | 10.1 | 14.0 | 13.1 | 15.6 | 14.8 | 12.7 | 12.3 | 11.2 |
| Posterior-SSP | 10.5 | 11.3 | 9.0 | 11.7 | 12.7 | 14.4 | 14.4 | 12.2 | 12.1 | 9.3 |
| Superior-INF | 12.5 | 12.3 | 9.3 | 15.2 | 13.3 | 15.4 | 14.3 | 13.4 | 13.7 | 12.8 |
| Sup.Mid.-INF | 13.7 | 14.2 | 10.4 | 16.8 | 13.4 | 17.3 | 15.2 | 15.6 | 15.9 | 15.4 |
| Inf.Mid.-INF | 14.5 | 13.9 | 11.1 | 18.3 | 16.0 | 18.5 | 16.7 | 17.1 | 18.5 | 15.7 |
| Inferior-INF | 15.2 | 14.2 | 12.2 | 19.5 | 17.9 | 20.7 | 17.5 | 18.6 | 15.5 | 15.5 |
| Teres minor | 9.3 | 9.7 | 9.5 | 13.4 | 12.3 | 12.1 | 12.0 | 12.4 | 11.9 | 11.0 |
Table A.6.
Fascicle length (cm) for each muscle sub-region and each specimen
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Anterior-SSP | 5.8 | 6.0 | 7.4 | 9.7 | 8.3 | 10.7 | 7.3 | 7.4 | 7.4 | 8.0 |
| Middle-SSP | 7.7 | 7.6 | 8.0 | 11.1 | 8.7 | 10.4 | 11.3 | 7.8 | 8.1 | 6.6 |
| Posterior-SSP | 6.2 | 9.1 | 7.5 | 9.0 | 9.1 | 10.7 | 10.6 | 8.5 | 7.9 | 8.6 |
| Superior-INF | 5.6 | 6.5 | 8.8 | 13.1 | 9.4 | 8.5 | 10.5 | 7.5 | 6.8 | 11.0 |
| Sup.Mid.-INF | 5.9 | 8.1 | 9.1 | 12.1 | 7.5 | 12.9 | 12.0 | 8.2 | 5.6 | 10.5 |
| Inf.Mid.-INF | 4.3 | 9.5 | 8.2 | 13.8 | 12.1 | 13.3 | 11.3 | 11.4 | 6.8 | 12.9 |
| Inferior-INF | 4.0 | 9.5 | 10.6 | 11.1 | 10.1 | 11.7 | 10.5 | 13.0 | 5.8 | 12.7 |
| Teres minor | 3.4 | 7.4 | 7.5 | 7.2 | 10.0 | 9.9 | 10.4 | 7.6 | 8.4 | 8.8 |
Table A.7.
Mean sarcomere length (lm) for each muscle sub-region and each specimen
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Anterior-SSP | 3.03) | 2.59 | 2.89 | 2.71 | 2.52 | 3.23 | 3.02 | 2.56 | 3.14 | 3.42 |
| Middle-SSP | 2.75 | 2.73 | 2.70 | 2.92 | 2.53 | 3.18 | 3.21 | 2.56 | 3.07 | 3.48 |
| Posterior-SSP | 2.69 | 2.61 | 2.74 | 3.26 | 2.78 | 2.90 | 3.10 | 2.67 | 3.27 | 3.44 |
| Superior-INF | 2.26 | 2.94 | 2.67 | 3.20 | 2.84 | 3.28 | 3.36 | 2.83 | 3.31 | 3.54 |
| Sup.Mid.-INF | 2.30 | 3.02 | 2.80 | 3.27 | 2.69 | 3.35 | 3.25 | 3.19 | 3.33 | 3.47 |
| Inf.Mid.-INF | 2.37 | 3.08 | 2.73 | 3.24 | 2.75 | 3.32 | 3.12 | 2.78 | 3.35 | 3.41 |
| Inferior-INF | 2.16 | 3.06 | 2.45 | 3.15 | 2.65 | 3.17 | 3.13 | 2.70 | 3.26 | 3.38 |
| Teres minor | 1.93 | 2.79 | 2.12 | 2.95 | 2.33 | 3.00 | 3.03 | 2.81 | 2.73 | 2.95 |
Table A.8.
Optimal fascicle length (cm) for each muscle sub-region and each specimen
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Anterior-SSP | 5.4 | 6.5 | 7.2 | 10.0 | 9.2 | 9.3 | 6.8 | 8.1 | 6.6 | 6.5 |
| Middle-SSP | 7.9 | 7.8 | 8.3 | 10.6 | 9.6 | 9.2 | 9.9 | 8.5 | 7.4 | 5.3 |
| Posterior-SSP | 6.5 | 9.7 | 7.7 | 7.7 | 9.2 | 10.3 | 9.6 | 8.9 | 6.8 | 7.0 |
| Superior-INF | 7.0 | 6.2 | 9.2 | 11.5 | 9.3 | 7.3 | 8.7 | 7.4 | 5.8 | 8.7 |
| Sup.Mid.-INF | 7.2 | 7.5 | 9.1 | 10.4 | 7.8 | 10.8 | 10.3 | 7.2 | 4.7 | 8.5 |
| Inf.Mid.-INF | 5.1 | 8.6 | 8.4 | 11.9 | 12.3 | 11.2 | 10.1 | 11.5 | 5.7 | 10.6 |
| Inferior-INF | 5.2 | 8.7 | 12.1 | 9.9 | 10.7 | 10.3 | 9.4 | 13.5 | 5.0 | 10.5 |
| Teres minor | 4.9 | 7.4 | 9.9 | 6.8 | 12.0 | 9.2 | 9.6 | 7.6 | 8.6 | 8.4 |
Table A.9.
Optimal muscle length (cm) for each muscle sub-region and each specimen
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Anterior-SSP | 9.3 | 10.0 | 7.8 | 12.2 | 12.7 | 10.6 | 9.3 | 14.1 | 10.4 | 7.5 |
| Middle-SSP | 12.0 | 9.0 | 10.5 | 13.4 | 14.5 | 13.7 | 12.9 | 13.9 | 11.2 | 9.0 |
| Posterior-SSP | 10.9 | 12.1 | 9.2 | 10.0 | 12.8 | 13.9 | 13.0 | 12.8 | 10.4 | 7.6 |
| Superior-INF | 15.5 | 11.7 | 9.8 | 13.3 | 13.1 | 13.1 | 11.9 | 13.3 | 11.6 | 10.1 |
| Sup.Mid.-INF | 16.7 | 13.2 | 10.4 | 14.4 | 13.9 | 14.5 | 13.1 | 13.7 | 13.4 | 12.4 |
| Inf.Mid.-INF | 17.2 | 12.6 | 11.4 | 15.8 | 16.3 | 15.6 | 15.0 | 17.2 | 15.5 | 12.9 |
| Inferior-INF | 19.7 | 13.0 | 14.0 | 17.4 | 18.9 | 18.3 | 15.7 | 19.3 | 13.3 | 12.8 |
| Teres minor | 13.5 | 9.7 | 12.5 | 12.7 | 14.8 | 11.3 | 11.1 | 12.4 | 12.2 | 10.4 |
Table A.10.
Maximum external rotation moment arm (cm) at 10 abduction for each muscle sub-region and each specimen
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Anterior-SSP | 0.46 | 1.10 | 1.44 | 0.22 | 1.01 | 1.70 | 0.89 | 0.17 | 0.78 | 0.51 |
| Middle-SSP | 1.21 | 1.34 | 1.86 | 1.22 | 1.44 | 2.59 | 2.15 | 1.06 | 1.48 | 1.03 |
| Posterior-SSP | 1.42 | 1.40 | 2.05 | 1.60 | 1.08 | 1.84 | 1.63 | 1.16 | 1.45 | 0.80 |
| Superior-INF | 2.26 | 2.28 | 2.94 | 2.05 | 2.23 | 3.38 | 2.25 | 2.32 | 1.91 | 2.03 |
| Sup.Mid.-INF | 2.27 | 2.68 | 3.12 | 2.56 | 2.43 | 3.21 | 2.67 | 2.73 | 2.08 | 2.39 |
| Inf.Mid.-INF | 2.47 | 2.83 | 3.34 | 2.14 | 2.44 | 3.52 | 2.63 | 2.86 | 2.18 | 2.41 |
| Inferior-INF | 2.45 | 2.73 | 2.67 | 1.79 | 1.89 | 3.33 | 2.64 | 2.58 | 2.19 | 1.97 |
| Teres minor | 2.01 | 2.85 | 2.63 | 2.37 | 1.66 | 2.70 | 2.29 | 2.52 | 1.44 | 2.30 |
Table A.11.
Maximum external rotation moment arm (cm) at 60 abduction for each muscle sub-region and each specimen
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Anterior-SSP | 0.49 | 0.71 | 0.82 | 0.62 | 0.46 | 1.07 | 0.42 | 0.81 | 0.62 | 0.34 |
| Middle-SSP | 0.71 | 0.61 | 0.98 | 0.51 | 0.91 | 0.91 | 0.82 | 0.62 | 1.12 | 0.40 |
| Posterior-SSP | 0.91 | 0.89 | 0.97 | 0.62 | 0.75 | 0.82 | 1.16 | 0.72 | 0.62 | 0.68 |
| Superior-INF | 1.49 | 1.62 | 1.54 | 1.30 | 1.72 | 1.89 | 1.78 | 1.42 | 1.29 | 1.29 |
| Sup.Mid.-INF | 1.48 | 1.44 | 1.93 | 1.62 | 1.86 | 1.63 | 1.74 | 1.98 | 1.77 | 1.01 |
| Inf.Mid.-INF | 1.82 | 1.33 | 2.30 | 1.66 | 2.12 | 1.84 | 1.42 | 2.20 | 1.68 | 1.27 |
| Inferior-INF | 1.90 | 1.70 | 2.22 | 1.80 | 2.20 | 1.86 | 1.66 | 1.95 | 1.94 | 1.35 |
| Teres minor | 2.25 | 2.54 | 2.53 | 2.10 | 2.37 | 3.21 | 2.44 | 2.90 | 2.19 | 1.97 |
Acknowledgements
We thank Charles Roehm and Dennis Kayner for fabrication of instrumentation, Laurie Huston and Tom With-row for assistance with harvesting of specimens, and Matt Lungren for measurement of sarcomere lengths. This study was supported by grants from the Whitaker Foundation and the National Institutes of Health (AR048540).
References
- Amis AA, Dowson D, Wright V. Muscle strengths and musculo-skeletal geometry of the upper limb. Engineering in Medicine. 1979;8:41–48. [Google Scholar]
- An KN, Hui FC, Morrey BF, Linscheid RL, Chao EY. Muscles across the elbow joint: a biomechanical analysis. Journal of Biomechanics. 1981;14:659–669. doi: 10.1016/0021-9290(81)90048-8. [DOI] [PubMed] [Google Scholar]
- Bassett RW, Browne AO, Morrey BF, An KN. Glenohumeral muscle force and moment mechanics in a position of shoulder instability. Journal of Biomechanics. 1990;23:405–415. doi: 10.1016/0021-9290(90)90295-e. [DOI] [PubMed] [Google Scholar]
- Brand PW, Beach RB, Thompson DE. Relative tension and potential excursion of muscles in the forearm and hand. The Journal of Hand Surgery. 1981;6:209–219. doi: 10.1016/s0363-5023(81)80072-x. [DOI] [PubMed] [Google Scholar]
- Chang YW, Su FC, Wu HW, An KN. Optimum length of muscle contraction. Clinical Biomechanics. 1999;14:537–542. doi: 10.1016/s0268-0033(99)00014-5. [DOI] [PubMed] [Google Scholar]
- Davidson PL, Chalmers DJ, Wilson BD. Stochastic-rheological simulation of free-fall arm impact in children: application to playground injuries. Computer Methods in Biomechanics and Biomedical Engineering. 2004;7:63–71. doi: 10.1080/1025584042000206461. [DOI] [PubMed] [Google Scholar]
- Delp SL, Suryanarayanan S, Murray WM, Uhlir J, Triolo RJ. Architecture of the rectus abdominus, quadratus lumborum and erector spinae. Journal of Biomechanics. 2001;34:371–375. doi: 10.1016/s0021-9290(00)00202-5. [DOI] [PubMed] [Google Scholar]
- Hoffer JA, Caputi AA, Pose IE, Griffiths RI. Roles of muscle activity and load on the relationship between muscle spindle length and whole muscle length in the freely walking cat. Progress in Brain Research. 1989;80:75–85. doi: 10.1016/s0079-6123(08)62201-3. [DOI] [PubMed] [Google Scholar]
- Hoy MG, Zajac FE, Gordon ME. A musculoskeletal model of the human lower extremity: the effect of muscle, tendon, and moment arm on the moment-angle relationship of musculotendon actuators at the hip, knee, and ankle. Journal of Biomechanics. 1990;23:157–169. doi: 10.1016/0021-9290(90)90349-8. [DOI] [PubMed] [Google Scholar]
- Hughes RE, An K-N. Monte Carlo simulation of a planar shoulder model. Medical & Biological Engineering &Computing. 1997;35:544–548. doi: 10.1007/BF02525538. [DOI] [PubMed] [Google Scholar]
- Hughes RE, Niebur G, Liu J, An K-N. Comparison of two methods for computing abduction moment arms of the rotator cuff. Journal of Biomechanics. 1998;31:157–160. doi: 10.1016/s0021-9290(97)00113-9. [DOI] [PubMed] [Google Scholar]
- Kuechle DK, Newman SR, Itoi E, Morrey BF, An K-N. Shoulder muscle moment arms during horizontal flexion and elevation. Journal of Shoulder and Elbow Surgery. 1997;6:429–439. doi: 10.1016/s1058-2746(97)70049-1. [DOI] [PubMed] [Google Scholar]
- Kuechle DK, Newman SR, Itoi E, Niebur GL, Morrey BF, An K-N. The relevance of the moment arm of shoulder muscles with respect to axial rotation of the glenohumeral joint in four positions. Clinical Biomechanics. 2000;15:322–329. doi: 10.1016/s0268-0033(99)00081-9. [DOI] [PubMed] [Google Scholar]
- Langenderfer J, Jerabek SA, Thangamani VB, Kuhn JE, Hughes RE. Musculoskeletal parameters of muscles crossing the shoulder and elbow and the effect of sarcomere length sample size on estimation of optimal muscle length. Clinical Biomechanics. 2004;19:664–670. doi: 10.1016/j.clinbiomech.2004.04.009. [DOI] [PubMed] [Google Scholar]
- Langenderfer JE, Patthanacharoenphon C, Hughes RE, Carpenter JE. Variability of glenohumeral external rotator muscle moment arms. Proceedings, XX Congress of the International Society of Biomechanics and 29th Annual Meeting of the American Society of Biomechanics, Cleveland, OH.2005. [Google Scholar]
- Lieber RL, Friden J. Intraoperative measurement and biomechanical modeling of the flexor carpi ulnaris-to-extensor carpi radialis longus tendon transfer. Journal of Biomechanical Engineering. 1997;119:386–391. doi: 10.1115/1.2798283. [DOI] [PubMed] [Google Scholar]
- Lieber RL, Fazeli BM, Botte MJ. Architecture of selected wrist flexor and extensor muscles. The Journal of Hand Surgery. 1990;15A:244–250. doi: 10.1016/0363-5023(90)90103-x. [DOI] [PubMed] [Google Scholar]
- Lieber RL, Loren GJ, Friden J. In vivo measurement of human wrist extensor muscle sarcomere length changes. Journal of Neurophysiology. 1994;71:874–881. doi: 10.1152/jn.1994.71.3.874. [DOI] [PubMed] [Google Scholar]
- Loren GJ, Lieber RL. Tendon biomechanical properties enhance human wrist muscle specialization. Journal of Biomechanics. 1995;28:791–799. doi: 10.1016/0021-9290(94)00137-s. [DOI] [PubMed] [Google Scholar]
- Loren GJ, Shoemaker SD, Burkholder TJ, Jacobson MD, Friden J, Lieber RL. Human wrist motors: biomechanical design and application to tendon transfers. Journal of Biomechanics. 1996;29:331–342. doi: 10.1016/0021-9290(95)00055-0. [DOI] [PubMed] [Google Scholar]
- McGough RL, Debski RE, Taskiran E, Fu FH, Woo SL-Y. Mechanical properties of the long head of the biceps tendon. Knee Surgery, Sports Traumatology, Arthroscopy. 1996;3:226–229. doi: 10.1007/BF01466622. [DOI] [PubMed] [Google Scholar]
- McLean SG, Su A, van den Bogert AJ. Development and validation of a 3-D model to predict knee loading during dynamic movement. Journal of Biomechanical Engineering. 2003;125:864–874. doi: 10.1115/1.1634282. [DOI] [PubMed] [Google Scholar]
- Murray WM, Buchanan TS, Delp SL. The isometric functional capacity of muscles that cross the elbow. Journal of Biomechanics. 2000;33:943–952. doi: 10.1016/s0021-9290(00)00051-8. [DOI] [PubMed] [Google Scholar]
- Otis JC, Jiang C-C, Wickiewicz TL, Peterson MGE, Warren RF, Santner TJ. Changes in the moment arms of the rotator cuff and deltoid muscles with abduction and rotation. The Journal of Bone and Joint Surgery. 1994;76-A:667–676. doi: 10.2106/00004623-199405000-00007. [DOI] [PubMed] [Google Scholar]
- Portney LG, Watkins MP. Foundations of Clinical Research: Applications to Practice. Appleton &Lange; Norwalk, CT: 1993. Statistical measures of reliability; pp. 511–516. [Google Scholar]
- Valero-Cuevas FJ, Johanson ME, Towles JD. Towards a realistic biomechanical model of the thumb: the choice of kinematic description may be more critical than the solution method or the variability/uncertainty in musculoskeletal parameters. Journal of Biomechanics. 2003;36:1019–1030. doi: 10.1016/s0021-9290(03)00061-7. [DOI] [PubMed] [Google Scholar]
- Veeger HEJ, van Der Helm FCT, Van Der Woude LHV, Pronk GM, Rozendal RH. Inertia and muscle contraction parameters for musculoskeletal modeling of the shoulder mechanism. Journal of Biomechanics. 1991;24:615–629. doi: 10.1016/0021-9290(91)90294-w. [DOI] [PubMed] [Google Scholar]
- Veeger HEJ, Yu B, An K-N, Rozendal RH. Parameters for modeling the upper extremity. Journal of Biomechanics. 1997;30:647–652. doi: 10.1016/s0021-9290(97)00011-0. [DOI] [PubMed] [Google Scholar]
- Walker SM, Schrodt R. I segment lengths and thin filament periods in skeletal muscle fibers of the rhesus monkey and the human. Anatomical Record. 1974;178:63–82. doi: 10.1002/ar.1091780107. [DOI] [PubMed] [Google Scholar]
- Woo SLY, Danto MI, Ohland KJ, Lee TQ, Newton PO. The use of a laser micrometer system to determine the cross-sectional shape and area of ligaments: a comparative study with two existing methods. Journal of Biomechanical Engineering. 1990;112:426–431. doi: 10.1115/1.2891206. [DOI] [PubMed] [Google Scholar]
- Zajac FE. Muscle and tendon: properties, models, scaling, and application to biomechanics and motor control. Critical Reviews in Biomedical Engineering. 1989;17:359–411. [PubMed] [Google Scholar]