Direct evidence for local oscillatory current sources and intracortical phase gradients in turtle visual cortex

Abstract

Visual stimuli induce oscillations in the membrane potential of neurons in cortices of several species. In turtle, these oscillations take the form of linear and circular traveling waves. Such waves may be a consequence of a pacemaker that emits periodic pulses of excitation that propagate across a network of excitable neuronal tissue or may result from continuous and possibly reconfigurable phase shifts along a network with multiple weakly coupled neuronal oscillators. As a means to resolve the origin of wave propagation in turtle visual cortex, we performed simultaneous measurements of the local field potential at a series of depths throughout this cortex. Measurements along a single radial penetration revealed the presence of broadband current sources, with a center frequency near 20 Hz (γ band), that were activated by visual stimulation. The spectral coherence between sources at two well-separated loci along a rostral–caudal axis revealed the presence of systematic timing differences between localized cortical oscillators. These multiple oscillating current sources and their timing differences in a tangential plane are interpreted as the neuronal activity that underlies the wave motion revealed in previous imaging studies. The present data provide direct evidence for the inference from imaging of bidirectional wave motion that the stimulus-induced electrical waves in turtle visual cortex correspond to phase shifts in a network of coupled neuronal oscillators.

Stimulus-induced oscillations are a hallmark of neuronal dynamics in many sensory systems (1). In the visual system of mammals, stimulus-induced oscillations occur along the entire visual as well as visual–motor system (2, 3). Further, the magnitude and spatial extent of these oscillations are modulated by the visual stimulus (4, 5). Theoretical studies on networks of neuronal oscillators (6, 7) and on physical systems with short-range interactions (8, 9) demonstrate that traveling electrical waves, i.e., nonzero time or phase differences between neuronal oscillators, are an emergent property of systems with spatially restricted connectivity. Examples that bear out these predictions are found in the central olfactory organs of some species, in which electrical oscillations are part of traveling electrical waves (10–12). The pattern of connections between neighboring regions in visual cortex would also be expected to lead to traveling electrical waves. Unexpectedly, in mammalian visual cortex traveling waves of electrical activity are usually not reported, i.e., the stimulus-induced electrical activity is coherent with zero-phase shift.

The visual area of turtle dorsal cortex exhibits electrical oscillations in response to natural visual stimuli (13, 14), similar to those in mammalian visual areas. The oscillations in turtle cortex occur with spectral peaks in the 15–25 Hz range, typically 20 Hz, and persist throughout many seconds of visual stimulation. In contrast to the apparent absence of visually induced traveling electrical waves in mammalian visual systems, such waves have been seen in turtle visual cortex. In particular, imaging experiments on cortex stained with a voltage-sensitive dye revealed oscillatory electrical waves that appear to propagate across the dorsal cortex in response to visual stimuli (15). The spatial pattern corresponds primarily to linear traveling waves that move along a caudal–rostral axis, parallel to the border between the D1 and D2 areas of dorsal cortex, along with brief epochs of circular traveling waves. The basis or origin of the timing differences in neuronal activity that lead to these waves was not addressed in previous studies.

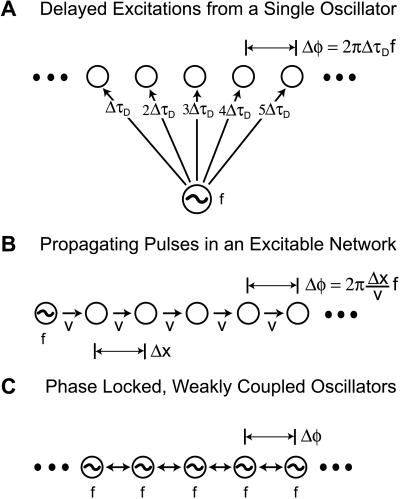
Wave motion may nominally appear from one of three mechanisms: (i) Apparent wave motion may originate as a consequence of a common pacemaker that directly excites neighboring regions of cortex through a progression of time delays (Fig. 1A). In this case, the wave motion is fictive, much like the lights on the marquee of a theater. An example is the wave of current discharge along the length of the electric eel (16). (ii) Wave motion may originate from a single oscillatory pacemaker region that periodically launches pulses. These pulses actively propagate along cortex. In this case, wave motion depends on the transmission of excitation between neurons (Fig. 1B). These waves appear in the nerve net of coelenterates, where one pacemaker at a time governs the initiation of waves (17) and in disinhibited slices (18, 19) and the developing retina (20, 21), where the waves are not necessarily periodic. (iii) Wave motion may originate as stable differences in phase among a network of oscillators that interact via weak predominantly short-range connections (Fig. 1C). Phase locking occurs among oscillators with sufficiently small differences in their intrinsic frequency (9). Such waves occur in the spinal swim circuit of the lamprey (22) and in the central olfactory lobe of the invertebrate Limax (11), where it has been shown that small isolated fractions of the lobe behave as independent oscillators, and that larger isolated segments produce traveling waves (23, 24).

Figure 1.

Cartoon of different models for the appearance of phase or timing differences tangential along cortex. Open circles indicate excitable, not necessarily oscillatory, tissue, whereas circles with ≈ indicate local oscillators. For simplicity, only one-dimensional models are shown. Note that phase differences, Δφ, and timing differences, Δτ are related here by Δφ = 2π Δτf, where f is the frequency of the oscillation. (A) A model where the wave motion is apparent and results from a single oscillator that drives adjacent regions of cortex through increasing time delays of Δτ_D. (B) A model where the wave motion originates from the transmission of pulses along a network of cortical neurons. In this example, a single oscillator launches the pulses. The propagation speed is denoted by v, and the distance between spatial loci is denoted by Δx, so that the time delay between loci is Δx/v. (C) A model where the wave motion originates as stable differences in phase among a network of oscillators that interact via weak short-range connections (shown here as only nearest-neighbor connections). The values of the phase shifts depend on details of the neuronal activation and interactions.

The data from previous imaging experiments show that the direction of propagation in a part of turtle dorsal cortex changes with the progression from linear to circular waves. Such a change in relative timing across cortex is unlikely to be accomplished by a hardwired common pacemaker (Fig. 1A) or an active wave with a single pacemaker (Fig. 1B), but is compatible with changes in timing in a network of interacting oscillators (Fig. 1C). Here we test the hypothesis that the visual cortex of turtle consists of localized oscillators, with timing or phase differences between them at different loci. We assay for localized rhythmic current sources or sinks as a function of depth along radial axes through cortex, i.e., normal to the cortical surface, and we further assay for timing differences between pairs of rhythmic current sources or sinks in the tangential plane.

We used multisite Si-based radial multielectrode arrays to simultaneously measure the local field potential (LFP) at a set of depths throughout visual cortex. These probes are miniature knife blades with isolated iridium pads along one face, which form a linear array of electrodes. The measured LFPs were used to compute the current source density (CSD) along the radial anatomical direction. Each change in sign of the CSD as a function of depth denotes a change in the local divergence of current flow along the radial direction and corresponds to the presence of oscillatory current sources or sinks. In contrast, a CSD that maintains constant sign as a function of depth is indicative of a region that is driven solely by an oscillator located far from the radial penetration, i.e., far on the scale of the thickness of the cortex. Thus, CSD analysis provides a means to determine whether the oscillations in electrical activity are driven by local oscillators as opposed to oscillatory input from a distant generator. Our approach is similar to that used to characterize thalamocortical spindles in cortex (25, 26). Furthermore, we used two Si-based arrays to identify current sources and sinks in neighboring radii and to determine the timing or phase differences between tangentially separated sources or sinks of oscillatory current.

Methods

Preparation.

Our data sets were obtained from 15 pond turtles, Pseudemys scripta, of mixed sex and with 15–20 cm carapace, purchased from Kons Scientific (Germantown, WI), and maintained locally. The semiisolated brain preparation described by Vasilescu (27) was used. In brief, under anesthesia by cold narcosis the head was isolated and cranial nerves IV through XII were cut to eliminate nociceptive input but leave vision and pupillary accommodation intact. Both common carotids were catheterized and the head continuously perfused with a blood substitute that consisted of 9.6 mM NaCl, 2.6 mM KCl, 4.0 mM CaCl₂, 2.0 mM MgCl₂, 32 mM NaHCO₃, 10 mM dextrose, and 1.5% (wt/vol) 60–90 kDa dextran and maintained at pH 7.4 with 5% (vol/vol) CO₂ in O₂. All procedures were approved by an Institutional Animal Care and Use Committee.

Stimulus.

The “step” stimulus for the surface-mapping experiments was a diffuse green light (28). The “looming” stimulus (29) for the measurements of depth profiles of LFP with Si-based arrays was a 13-cm-diameter white ball illuminated by diffuse white light (intensity approximately 10⁻⁶ W/cm²). The ball moved along a radial axis from the eye along a computer-controlled slide (MCS X30; Cyber Research, Branford, CT) at a speed of 3.8 cm/s from an initial position 27 cm from the eye to a final position, after 4 s, 8 cm away. The loom leads to a prolonged persistent oscillation in dorsal cortex (14). The effect of the looming stimulus on the accommodation of the eye, a qualitative indicator of the health of the preparation, was measured by selectively illuminating the pupil with infrared (910 nm) light and video recording the pupil during the loom. We extracted from the video record changes in area of the pupil, which are proportional to changes in the focal length of the lens as the animal accommodates in focus.

Anatomy.

The border between the D1 and D2 areas of dorsal cortex was determined for animals used in the surface potential measurements. The locations of the surface array were photographed at the time of the measurements. Further, the exposed surface of the turtle cortex was labeled with pin holes near the epicenter of the response, and these were further photographed; these marks served as fiducials to relate the location of the D1/D2 border relative to the locations of the array wires. The brain was subsequently sectioned at 30 μm and stained with cresyl violet. The D1/D2 border was defined by differences in cell packing and the width of the subcellular layer (30). The thickness of the cortex measured from the pia mater to the underlying ventricle is approximately 550 μm throughout D1 and widens to approximately 700 μm in D2 (30).

Electrophysiology.

Single measurements of the LFP were made with a tungsten electrode (WE300325A; Microprobe, Garden Grove, CA) that was positioned in 100-μm steps of depth to determine the radial profile of the LFP in successive measurements. Surface potentials were measured with a comb-like array of 16 silver-wire electrodes (50 μm diameter) that were polished at the tip and spaced at 300-μm intervals in contact with the pia mater. The Ag wires were held in a fixture so that the tips formed a line tangential to the cortical surface.

Potentials throughout the depth of the cortex were obtained simultaneously with a Si-based multielectrode array (16-CHAN-3) supplied by the Center for Neural Communication Technology (31) at the University of Michigan (Ann Arbor, MI). They consisted of an in-line radial array of 20 μm by 20 μm electrode contacts separated by 100 μm and plated with Ir. The utility of this array with turtle as well as mammalian cortex has been previously demonstrated (32, 33). In the present work, we recorded only from the deeper eight electrodes of each array; these span 700 μm from surface to depth. Before use, the Ir surfaces were electrically cleaned (±2-V square wave at 1 Hz for 10 cycles in 1 M KCl) and then “activated” (±0.7-V square wave at 1 Hz for 100 cycles in 1 M KCl) with a potentiostat. The final impedance of each electrode was 2 to 4 MΩ at 10 Hz, and each Si-based array could be used repeatedly.

Each electrode or electrode array was positioned radially with a piezoelectric drive (IW-700; Burleigh Instruments, Fishers, NY). The signal from each electrode, as well as a reference signal from an unrelated region of cortex, was impedance buffered with an N-channel field effect transistor (J201; Vishay Siliconix, Santa Clara, CA) in a common-source configuration that was placed close to the electrode. The buffered signals were differentially amplified (INA101; Burr Brown, Tucson, AZ) at a gain of 100, bandpass filtered (0.1-Hz single-pole high pass) (300-Hz 4-pole Bessel low pass; Frequency Devices, Haverhill, MA), further amplified with a gain between 32 and 128, and digitized at 1 kHz.

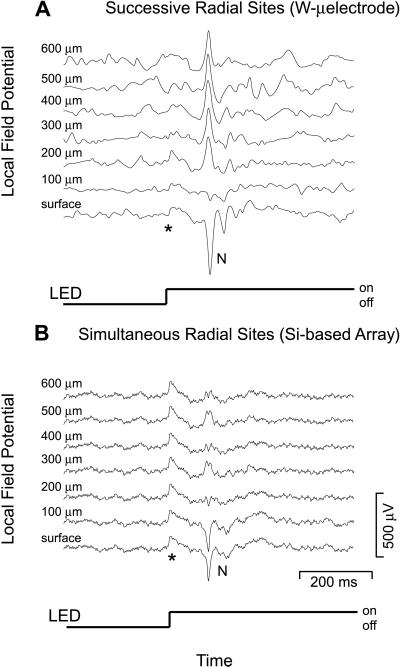
Compared with a conventional microwire electrode, the Si-based multisite electrode arrays have a large cross-section and, by construction, measure the potential at sites away from the tip of the array and only on one face of the array. As a means to test the sensitivity of the Si-based array, we compared signals recorded with the array to those from a nearby tungsten microwire. A transient cortical response was initiated by a step of light. We measured the LFP from a microwire placed sequentially at different depths, along with the LFP found from simultaneous measurements from the Si-based array inserted approximately 0.5 mm away from the microwire. We observed a substantially higher signal-to-noise ratio with the microwire (Fig. 2). Nonetheless, the major features observed with the microwire, particularly the transient surface potential (“N” in Fig. 2), are seen with the Si-based array. This implies that each electrode on the array makes a reliable measurement, and that damage to brain tissue from the array does not compromise our simultaneous measurements of local current flow.

Figure 2.

Comparison between the responses of successive tungsten (W) microelectrode loci vs. the Si-based multielectrode array. The amplitude and time scales are the same for both sets of records. (A) The single-trial local field potential at a series of successive depths, spaced 100 μm apart, observed in response to a step of illumination from a green light-emitting diode (LED), with a center wavelength of 569 nm, delivered through a diffuser to the contralateral eye. The intensity at the eye was approximately 10⁻⁵ W/cm². Each record represents an individual trial. Note the initial negative-going spike (N). The positive step at the onset of stimulation ✶ is an electronic artifact. (B) Simultaneous single-trial measurement of the local field potential from successive depths, obtained with the Si-based array, in response to a step of illumination.

Analysis.

The voltage signals measured along each Si-based array, denoted V_i^k(z, t) where the subscript i labels lateral location, and the superscript k labels the trial, were used to calculate the discrete second spatial derivative of the potential with respect to depth along the radial axis, denoted ẑ. This derived signal, −Δ²V(z, t)/Δz², is minus the ẑ component of the Laplacian of the LFP and is referred to as the CSD. It is estimated as:

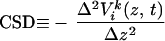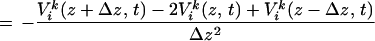where Δz = 100 μm. Changes in the sign of −Δ²V(z, t)/Δz² as a function of depth are interpreted as a change between a current source and sink (34); note that sources and sinks alternate in time for an oscillating current. The interpretation of this measure as an indicator of sources or sinks rests on numerous assumptions: (i) The dominant current flow is along a radial axis through cortex, consistent with the radial orientation of neurons in cortex. (ii) The conductivity of cortex, on the approximately 100-μm scale of our measurements, varies only weakly in value. (iii) There is a significant degree of temporal synchrony between current flow in neighboring neurons.

The spectral coherence is a complex-valued function of frequency, whose magnitude is a normalized measure of the covariation between each of the spectral components of two-time series and whose phase corresponds to the timing difference between each spectral component in the two-time series. The coherence across pairs of spatial components of the CSD (not the LFP) was calculated with a multitaper method (35). This method allowed us to achieve reliable estimates in single trials; typically, we estimated spectra in a 1-s sliding window with a bandwidth of 3 Hz. The sample variance of the average spectrum (averaged over all trials) was computed as a jackknife estimate. Details of these procedures in the context of neuronal data have been described (36). We principally concentrated on coherence of the 20-Hz band.

Results

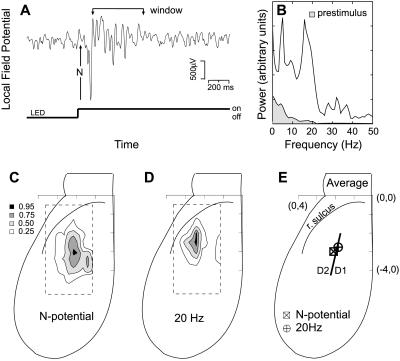
The locus of neuronal activity was determined from maps of the electrical response measured at the surface of cortex in response to a step of diffuse light. Data were taken over a 2.5- by 4.5-mm region with 0.25-mm resolution. We consider first the results for a single animal. The stimulus-evoked electrical signal consisted of a large negative peak (“N-potential” in Fig. 3A), which corresponds to depolarization of the superficial lamina (15), followed by a 0.5- to 1-s period of oscillating electrical activity. The oscillatory component, quantified in a 0.5-s window (“window” in Fig. 3A), was typically dominated by a spectral peak near 20 Hz (Fig. 3B); the lower frequency peak is not specific to visual stimuli (14). We mapped both the spatial localization of the amplitude of the N-potential (Fig. 3C) and the power in a spectral band centered at 20 Hz (4-Hz half-bandwidth) (Fig. 3D). The spatial distribution for the N-potential was typically broader than that for the 20-Hz oscillations (see Fig. 3 C and D). The two epicenters of the evoked responses were charted relative to the anatomical boundary between areas D1 and D2 of dorsal cortex (Methods). On average (n = 6 animals), the epicenters lie within 300 μm of each other and the boundary (Fig. 3E).§

Figure 3.

Spatial localization of the visually induced electrical response. The stimulus was a step of illumination from a green light-emitting diode (LED; parameters as in legend to Fig. 2). (A) Example of the surface potential in response to a single step. Note the initial negative-going spike (N-potential) and the subsequent fast oscillations that persist for up to 1 s. The epoch marked “window” corresponds to a 0.5-s poststimulus interval. (B) Power spectra of the “window” epoch in A. Note the stimulus-induced peak near 20 Hz, as well as the increased power at lower frequencies compared with a 0.5-s prestimulus window. The bandwidth of the spectral estimate (full width at half-maximal amplitude) was 4 Hz. (C) The locus of amplitudes of the N-potential. The gray-scale contours correspond to fractions of the maximal response. The spatial coordinate system originates at the medial line and the rostral edge of cortex. (D) The locus of response for the 20-Hz oscillatory band. (E) The trial-averaged centroids for the N-potential and 20-Hz oscillation band are shown relative the anatomical border between dorsal regions D1 and D2 (line); n = 6 animals.

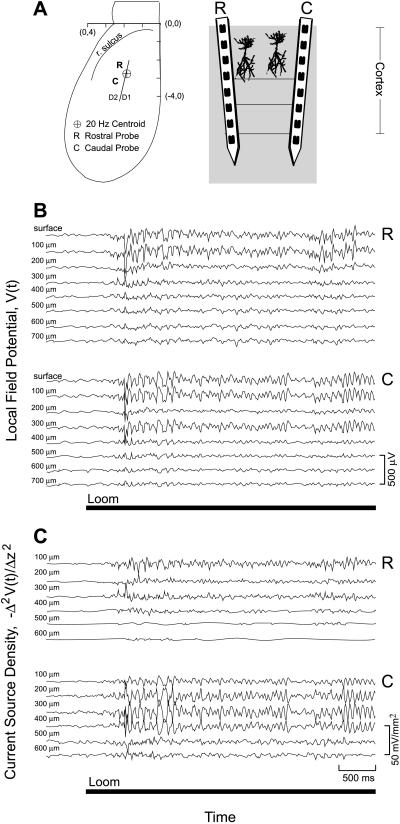
The phase of the oscillatory electrical activity is not time locked to the onset of the visual stimulus (13); thus, measurements of the LFP at different depths must be performed simultaneously as a means to identify sources or sinks of the oscillatory current. To accomplish this, we used pairs of Si-based arrays that were inserted radially into area D2, close to the epicenter of the response and along a line parallel to the rostral–caudal axis (Fig. 4A). The separation of the pair was 1.0 mm. We observed robust LFPs throughout the depth of visual cortex in response to the looming stimulus (Fig. 4B). The onset of heightened LFP activity began with a variable delay after the ball started to move. The CSD was computed from the measured potentials (Methods). Visual inspection shows that the oscillating part of the CSD changes in sign as a function of depth below the pia matter (Fig. 4C). Typically, the CSD exhibited two changes in sign (e.g., array “R” in Fig. 4C), consistent with current flow from proximal and basal dendrites to somata (and vice versa). In two records with exceptionally high signal-to-noise ratio (e.g., array “C” in Fig. 4C), a third change in sign in deeper layers was observed. These data demonstrate the presence of local sources of oscillatory current in visual cortex.

Figure 4.

Single-trial simultaneous depth profiles of the local field potential, V(t), and the current source density, −Δ²V(z, t)/Δz², in response to a looming ball. (A) (Left) Schematic of the location of the two Si-based arrays in dorsal-area D2, one caudal (C) and one rostral (R) relative to the centroid of the 20-Hz response (Fig. 2E). (Right) Schematic of the Si-based multielectrode arrays through the depth of cortex. (B) Single-trial measurement of the local field potentials at the two locations in A. The 4-s period of the loom is indicated by the thick bar. (C) The current source density, calculated from the data in B. Note that the lower two rostral traces and the lower three caudal traces have been multiplied by a factor of 2.

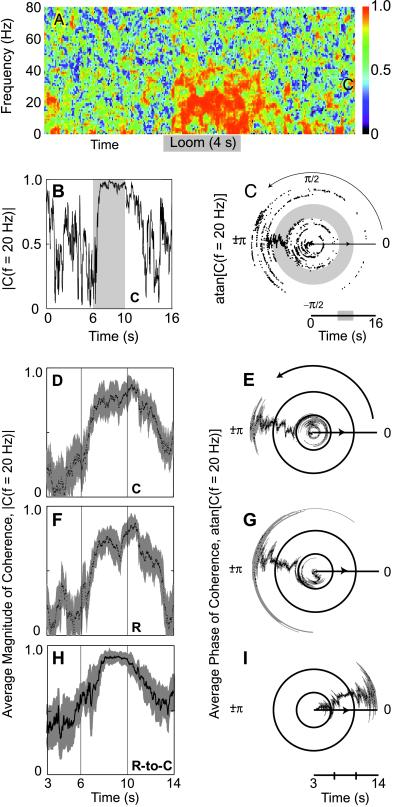
The correlations in the CSD between different depths of cortex were quantified in terms of the spectral coherence calculated for a sliding window as a function of time. For the data of Fig. 4C (100 μm and 200 μm channels in array “C”), we observed that the magnitude of the coherence was negligible at all but the lowest frequencies before the onset of the stimulus (Fig. 5A). However, during the duration of the loom there was significant coherence in a roughly 10- to 30-Hz band that subsequently decayed after the loom stopped (Fig. 5A).¶ The time dependence of the coherence in a band centered at 20 Hz can be seen clearly in a line plot. We observed that the magnitude of the coherence fluctuates rapidly before the onset of the loom and is likely to be insignificant, whereas the coherence remains steady near a value of 1 during the loom and is likely to be highly significant (Fig. 5B). Similarly, the phase of the coherence fluctuates rapidly before and subsequent to the loom but is essentially locked at a value near π radians during the loom (Fig. 5C). The value of π radians is consistent with a reversal of current flow between oscillators at these two laminae in cortex. The multiple trial average response for both arrays shows that the phase difference of π radians is robust (Fig. 5 D–G). In general, shifts at or near π radians were observed across laminae in all successful penetrations within the centroid of the 20-Hz response (Fig. 2E) (n = 10 sites distributed among 6 animals).

Figure 5.

Spectral coherence of the current source density between intra- and interradial locations. (A) The magnitude of the coherence between the upper source/sink pairs of the caudal of two Si-based arrays (100 μm and 200 μm in Fig. 4C) calculated from single-trial data as a function of frequency and time. The temporal window was 1 s and the bandwidth was 4 Hz. (B and C). Detailed view of the coherence calculation in A for the 20-Hz band. Shown is the magnitude, |C(f)|, and phase, arctangent [Im(C(f))/Re(C(f))], for f = 20 Hz. The gray band indicates the period of the looming stimulus. Note the high coherence during stimulation and the phase shift of near π radians between source/sink pairs. (D and E) The trial-averaged (n = 16) magnitude and phase of the coherence for the upper source/sink pairs of the caudally located array. The black line is the mean response, and the gray bands define the standard deviation. (F and G) The trial-averaged magnitude and phase of the coherence for the upper source/sink pairs of the rostral array. (H and I) The trial-averaged magnitude and phase of the coherence between the uppermost sources of the rostral and caudal arrays. Note the significant phase shift of +0.53 radians.

The relative phase difference between well-separated (1-mm) cortical regions was assayed through simultaneous records of current sources and sinks across the two Si-based arrays (Fig. 4A). For the data of Fig. 5, we observe significant coherence across the upper oscillatory sources or sinks in the frequency band centered at 20 Hz (Fig. 5H). The phase difference was +0.5 radians (Fig. 5I). The same phase shift was observed between the next lower sources or sinks, consistent with the reversal in sign of the CSD with depth (Fig. 5 E and G). The positive sign of the observed shift indicates that the oscillatory activity at the rostrally located array leads the caudal one. In general, we observed a shift of +0.4 ± 0.2 radians (mean ± SD) (n = 4 animals with dual array measurements). These shifts are direct evidence for wave motion along visual cortex.

Discussion

We have shown that visual stimulation leads to coherent oscillations among multiple pairs of current sources and sinks that lie along radii in depth in the visual cortex of turtles (Fig. 4). The coherent oscillations extend laterally over an area of cortex roughly 1 by 2 mm (Fig. 3D). Their epicenter lies near the anatomical border between areas D1 and D2 of dorsal cortex (Fig. 3E). We further showed that current sources in separate radii have a phase shift along a rostral–caudal axis that parallels the D1/D2 border; the same axis corresponds to the net orientation of the axons that mediate horizontal connections in dorsal cortex (38). The presence of local current sources and lateral phase shifts among these sources implies that the oscillatory waves of electrical activity in visual cortex (15) are generated by sources intrinsic to cortex (Fig. 1C), as opposed to being driven solely by a fixed external pacemaker (Fig. 1A) or a single local pacemaker (Fig. 1B). This conclusion is further supported by the appearance of waves that propagate in opposite directions across the same region of cortex during different epochs of time (15).

The phase gradients observed here, 0.4 radians/mm, are similar to the gradients seen across the epicenter of the response by optical imaging of the average membrane potential near the surface of cortex [arrow in Fig. 3e of Prechtl et al. (15)] and are a factor of 3 to 4 smaller than the largest gradient (15). The propagation speed of the wave through the epicenter may be estimated from the phase gradient as 2π f (Δφ/Δx)⁻¹ = 0.2 to 0.4 mm/ms. This speed is similar to the speed of horizontal propagation of subthreshold depolarization in visual cortex of monkey, 0.2 mm/ms, as inferred from optical imaging measurements (39). The speed is further similar to that for the spread of subthreshold depolarization in visual cortex of cat, 0.1 mm/ms, as inferred from intracellular measurements with cat (40). Note that the similarity in speeds does not imply that signal propagation in the mammalian preparations follows the same mechanism as that for wave motion in turtle cortex.

The mammalian cortex exhibits a multiplicity of rhythms that are modulated by the state of the animal (1). Some of these rhythms appear as linear waves that propagate across cortex (41–45), although the electrophysiological nature of these waves remains unknown. A paradoxical case is that of sleep spindles in neocortex (46). Current source-density measurements have shown that neocortex contains local sources or sinks for these oscillators (25), and direct stimulation of cortex leads to slowly propagating spindle waves (47). Yet in vivo measurements across cortex and thalamus find no evidence for traveling waves (47). A potentially similar paradox exists for the “40-Hz” oscillations associated with visual stimulation (2, 4, 5, 48). Perhaps data from simultaneous CSD measurements at multiple loci (Fig. 5) will resolve whether these oscillations are driven by an oscillatory pacemaker through uniform delays (Fig. 1A but with Δτ_D = 0) or are caused by coupled oscillators with synchronous activity (Fig. 1C with Δφ = 0).

The computational role of the phase gradient is an open issue. It is noteworthy that the gradient in turtle cortex is sufficiently small to make it unlikely that more than one region shares the same phase. In other words, the total shift across visual cortex does not exceed 2π radians (50 ms at 20 Hz) (15). Thus the oscillatory component of the membrane potential of neurons in different radii has an unambiguous phase, as opposed, for example, to the case where the shifts exceed 2π. Gradients with unambiguous phase provide a unique label that may be used to segment (49) or categorize (50, 51) the visual scene in the temporal domain.

Abbreviations

CSD

current source density

LFP

local field potential