Skip to main content
PMC home page
Plant Physiology logoLink to Plant Physiology
. 2002 Apr;128(4):1323–1331. doi: 10.1104/pp.010616

Rate of Dehydration and Cumulative Desiccation Stress Interacted to Modulate Desiccation Tolerance of Recalcitrant Cocoa and Ginkgo Embryonic Tissues1

Yongheng Liang 1, Wendell Q Sun 1,2,*
PMCID: PMC154260  PMID: 11950981

Abstract

Rate of dehydration greatly affects desiccation tolerance of recalcitrant seeds. This effect is presumably related to two different stress vectors: direct mechanical or physical stress because of the loss of water and physicochemical damage of tissues as a result of metabolic alterations during drying. The present study proposed a new theoretic approach to represent these two types of stresses and investigated how seed tissues responded differently to two stress vectors, using the models of isolated cocoa (Theobroma cacao) and ginkgo (Ginkgo biloba) embryonic tissues dehydrated under various drying conditions. This approach used the differential change in axis water potential (ΔΨ/Δt) to quantify rate of dehydration and the intensity of direct physical stress experienced by embryonic tissues during desiccation. Physicochemical effect of drying was expressed by cumulative desiccation stress [∫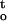Inline graphicf(ψ,t)], a function of both the rate and time of dehydration. Rapid dehydration increased the sensitivity of embryonic tissues to desiccation as indicated by high critical water contents, below which desiccation damage occurred. Cumulative desiccation stress increased sharply under slow drying conditions, which was also detrimental to embryonic tissues. This quantitative analysis of the stress-time-response relationship helps to understand the physiological basis for the existence of an optimal dehydration rate, with which maximum desiccation tolerance could be achieved. The established numerical analysis model will prove valuable for the design of experiments that aim to elucidate biochemical and physiological mechanisms of desiccation tolerance.

Drying rate affects desiccation tolerance or sensitivity of recalcitrant seed tissues significantly. Fast drying has been reported to allow the tissues of several recalcitrant seeds to achieve greater desiccation tolerance (Farrant et al., 1985, 1993; Normah et al., 1986; Berjak et al., 1990, 1992, 1993; Fu et al., 1990; Pammenter et al., 1991, 1999; Pritchard, 1991; Berjak and Pammenter, 1997; Kioko et al., 1998; Pritchard and Manger, 1998). Under slow drying conditions, seed tissues have to spend a longer period of time at intermediate water contents, at which aqueous-based deleterious processes occur. Thus, fast drying may minimize such deleterious effects associated with the dehydration of the metabolically active tissues (Pammenter et al., 1991; Côme and Corbineau, 1996; Berjak and Pammenter, 1997; Pritchard and Manger, 1998). Pammenter and Berjak (1999) reviewed drying rate effect on desiccation tolerance of recalcitrant seeds, and proposed that different deleterious mechanisms were probably involved in desiccation damage under different conditions. Liang and Sun (2000) recently found that there was an optimal drying rate for cocoa (Theobroma cacao) embryonic axes, and that both faster and slower drying were detrimental to achieve maximum desiccation tolerance. It was hypothesized that different stress vectors (e.g. physical and physicochemical effect) might interact to modulate desiccation tolerance or sensitivity of recalcitrant seeds (Liang and Sun, 2000).

A number of parameters such as water content, water activity, and water potential were used to describe water status in studies of seed desiccation tolerance (Roberts and Ellis, 1989; Vertucci and Roos, 1990, 1993; Pritchard 1991; Tompsett and Pritchard, 1993, 1998; Vertucci et al., 1994, 1995). Quantitative responses of plant seeds to water stress and temperature are commonly studied, using the hydrothermal time model that was proposed by Gummerson (1986). This empirical model has been further developed by the Bradford group (Bradford, 1990, 1995, 1996, 1997; Bradford and Somasco, 1994), and is presented by the following equation:

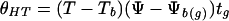graphic file with name M2.gif 1

where θHT is the hydrothermal time (megapascals-degree-days); T and Ψ are temperature and water potential of the environment, respectively; Tb and Ψb(g) are theoretic base temperature and base water potential, respectively; and tg is the time of response. Whereas the hydrothermal time model fits well the population-based experimental data under many conditions, it has been found that the underlying assumption of the model is not satisfied (Kebreab and Murdoch, 1999, 2000). A mathematical model based on thermodynamic considerations was suggested by Li et al. (1991), which used the activation energy as a measure of plant response to water stress. The activation energy model investigates plant responses at combinations of a series of water stress conditions and temperatures, and is able to identify the relative sensitivity of physiological and biochemical parameters to water stress. However, these two approaches cannot be used to study the effect of drying rate on desiccation tolerance of vegetative tissues and recalcitrant seeds. Neither the hydrothermal time model nor the activation energy model addresses the question of different stress vectors related to desiccation, and can be used to assess cumulative stress (time function) under desiccation conditions where water potential of plant tissue decreases steadily. The present study proposes a novel thermodynamic approach to carry out a quantitative analysis on the stress-time-response relationship. The response of plant tissues to desiccation is related to the thermodynamic status of tissue water, rather than to the actual water content. Thermodynamic parameters are directly related to numerous biophysical and physiological events that contribute to desiccation stress.

Water status of plant tissue can be measured by its chemical potential. The chemical potential of water (μw) in a system is described by:

graphic file with name M3.gif 2

where μ*w is the chemical potential of pure water at ideal reference conditions, R is the gas constant, T is absolute temperature, aw is water activity, 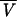Inline graphicw is the partial molar volume of water, P is the hydrostatic pressure in excess of atmospheric pressure, and mwgh is the gravitational term. The change in chemical potential of cellular water is a direct measure of desiccation stress. According to Equation 2, the difference in chemical potential of cellular water between two hydration states, A and B, can be described by:

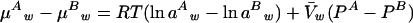graphic file with name M5.gif 3

The level of desiccation stress is, therefore, proportional to changes in osmotic potential and hydrostatic pressure in cells. In the present study, isolated recalcitrant cocoa and ginkgo (Ginkgo biloba) embryonic tissues were used as models for such a quantitative analysis of the stress-time-response relationship. The change of water potential during drying, ΔΨ/Δt, was used to express the instant rate of dehydration and to quantify the degree of desiccation stress. The integration of its time function [∫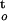Inline graphicf(ψ,t)] , represents the cumulative desiccation stress.

RESULTS

Change of Axis Water Potential under Controlled Desiccation Conditions

By applying the Ohm's law, water loss from embryonic axes can be described by the following equation:

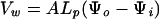graphic file with name M7.gif 4

where Vw, A, and Lp are the rate of water loss (m3 s−1), surface area (m2), and hydraulic conductivity (m s−1 pa−1), respectively, of axes. Ψo and Ψi are water potentials of drying air and axes, respectively. Under the controlled desiccation conditions used in the present study (i.e. constant relative humidity and temperature), the rate of water loss from axes depends mainly on changes in axis hydraulic conductivity and water potential during desiccation. Figure 1 shows changes in axis water content and water potential at relative humidities of 33%, 88%, and 94%. As reported previously (Li and Sun, 1999; Liang and Sun, 2000), water loss from axes followed a simple exponential function, until axes achieved the apparent equilibrium with drying air. The rate constant of water loss (β) was quantified through the following equation:

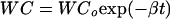graphic file with name M8.gif 5

where WCo is the initial water content, and t is time of drying.

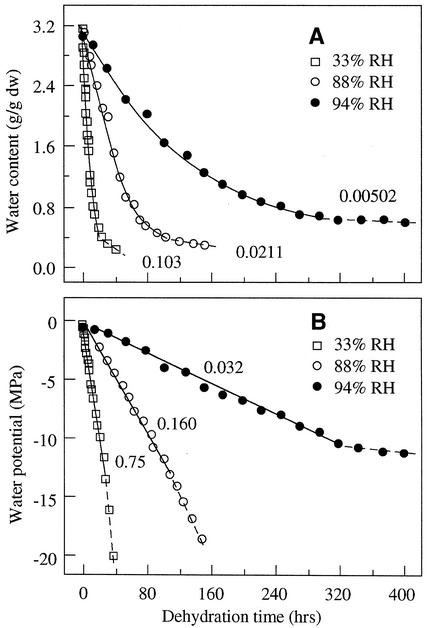
Figure 1.

Figure 1

Open in a new tab

Changes in water content (A) and water potential (B) in cocoa embryonic axes under three constant relative humidities at 16°C. Data points of the first drying phase in Figure 1A were fitted with an exponential function (solid lines), and the rate constant of water loss was shown near each drying curve. The decrease in water potential in Figure 1B followed a linear function during the first phase of drying, and the slope of the linear plots, ΔΨ/Δt, was rate of dehydration that measures desiccation stress intensity during drying. Note the change of the slope in Figure 1B at water potential around −12 to −15 MPa. Water in axis tissues at water potential below −12 to −15 MPa is osmotically inactive water and is held by matric and molecular forces. Similar results were obtained with axes dried at 25°C.

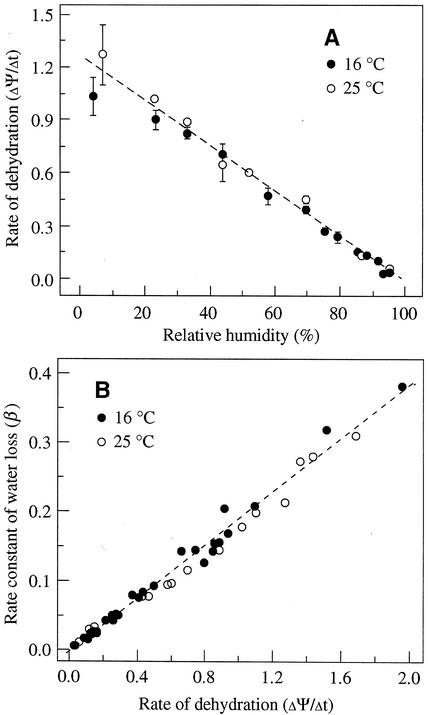
Water potential was measured by the equilibrium dehydration method through the desorption isotherm. Water potential decreased during dehydration. The decrease of water potential followed the zero-order kinetics at the first stage. The negative value of the slope (ΔΨ/Δt) of the first drying phase was used to express as rate of dehydration (Fig. 1B). Rate of dehydration (ΔΨ/Δt) decreased steadily as relative humidity increased (Fig. 2A). Figure 2B shows the linear relationship between rate of dehydration and rate constant of water loss during dehydration under various drying conditions at 16°C and 25°C.

Figure 2.

Figure 2

Open in a new tab

A, Rate of dehydration (ΔΨ/Δt) of cocoa embryonic axes under different humidity and temperature conditions. Vertical bars indicate ± sd under the same relative humidity. Bars smaller than the symbols were not shown. B, The relationship between rate constant of water loss (β) and rate of dehydration (ΔΨ/Δt).

Effect of Rate of Dehydration on Desiccation Tolerance

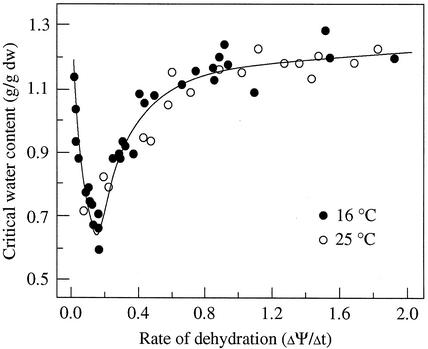
Desiccation tolerance of embryonic tissues was expressed with the critical water content, below which axis germination decreased significantly and electrolyte leakage increased greatly. The effect of rate of dehydration (ΔΨ/Δt) on desiccation tolerance of cocoa axes is shown in Figure 3. As rate of dehydration decreased, the critical water content decreased gradually at first, but then increased rapidly when rate of dehydration was very slow. An optimal rate of dehydration was observed at about 0.15 MPa h−1, which achieved the lowest critical water content about 0.6 g water g−1 dry weight in cocoa embryonic axes. A maximum desiccation tolerance level was previously reported at similar water content (Liang and Sun, 2000).

Figure 3.

Figure 3

Open in a new tab

The relationship between rate of dehydration and desiccation tolerance of cocoa embryonic axes. The methods used to determine critical water content was described elsewhere (Sun and Leopold, 1993; Li and Sun, 1999; Liang and Sun, 2000).

Evaluation of Cumulative Desiccation Stress

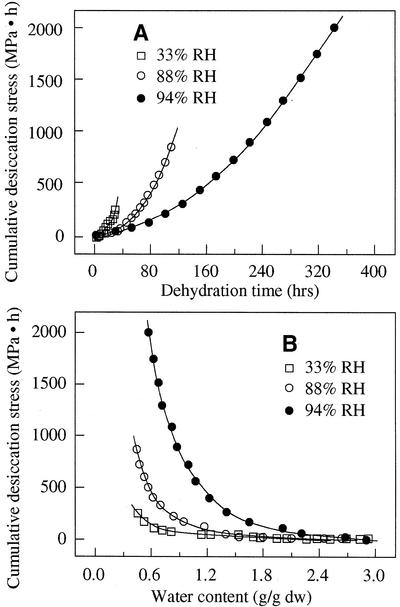
The effect of desiccation time on desiccation tolerance was evaluated using cumulative desiccation stress during drying. Cumulative desiccation stress of axes was quantified through the integration of the water potential/time function during dehydration [i.e. calculating the value of ∫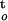Inline graphicf(ψ,t); Fig. 4]. Figure 5 shows the cumulative desiccation stress of axes during dehydration at relative humidities of 33%, 88%, and 94%. The level of cumulative desiccation stress depended on a number of factors, such as relative humidity, dehydration time, and final water content in axes. Under the rapid drying condition at low relative humidity (e.g. 33%), cumulative desiccation stress increased faster than under slow drying conditions (Fig. 5A). However, under the slow drying condition at high relative humidity (e.g. 94%), cumulative desiccation stress would be remarkably high as dehydration continued because dehydration time to achieve the same lower water content increased exponentially as rate of dehydration decreased (Fig. 5B). Therefore, axes that were dried to the same water content experienced greater cumulative desiccation stress under a slow dehydration condition than under a rapid drying condition (Fig. 5B). In other words, slow drying must impose much greater cumulative physiological stress.

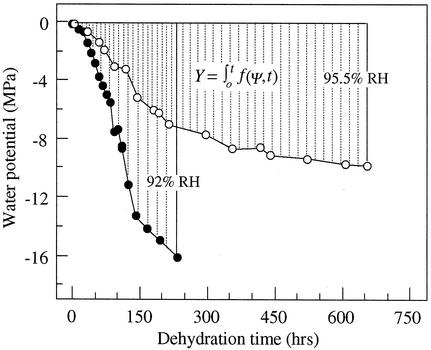
Figure 4.

Figure 4

Open in a new tab

Integration of water potential-time functions for cocoa embryonic axes dried under different humidity and temperature conditions. The integral, ∫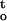Inline graphicf(ψ,t), expresses cumulative desiccation stress for embryonic axes dried for a period of time t, during which water potential of embryonic axes decreased from 0 to Ψ.

Figure 5.

Figure 5

Open in a new tab

Cumulative desiccation stress ∫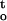Inline graphicf(ψ,t), of cocoa embryonic axes as the function of drying time (A) and residual water content (B) under three relative humidities at 16°C. Cumulative desiccation stress was calculated by integrating the water potential-time function, as shown in Figure 4.

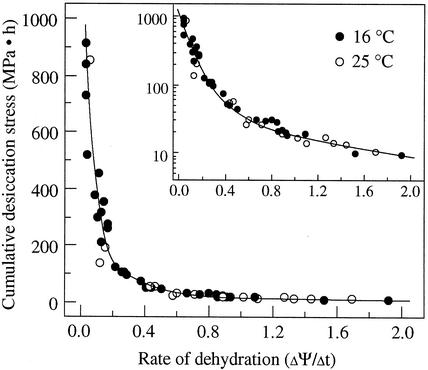
Figure 6 shows the level of cumulative desiccation stress when axes were dried to the respective critical water content at different rates of dehydration. Cumulative desiccation stress increased gradually as the rate of dehydration decreased from 2.0 to 0.3 MPa h−1. However, cumulative desiccation stress increased drastically when the rate of dehydration was lower than 0.2 MPa h−1.

Figure 6.

Figure 6

Open in a new tab

Cumulative desiccation stress [∫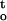Inline graphicf(ψ,t)] , of cocoa embryonic axes that were dried to the respective critical water content under different rate of dehydration at 16°C and 25°C. Inset, Cumulative desiccation stress were plotted on a logarithmic scale.

Effect of Cumulative Desiccation Stress on Desiccation Tolerance

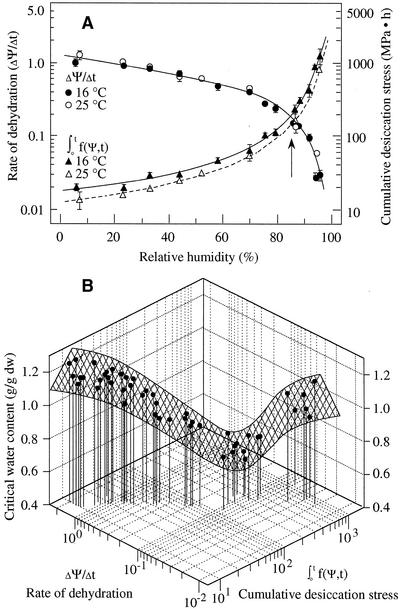
A multiple correlation/regression analysis on the relationship between desiccation tolerance, rate of dehydration (ΔΨ/Δt), and cumulative desiccation stress [∫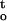Inline graphicf(ψ,t)] , was taken to examine the response of embryonic axes to two different types of stress vectors (i.e. direct mechanical or physical stress, and cumulative physicochemical stress). Figure 7A shows changes in ΔΨ/Δt (MPa h−1) and ∫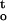Inline graphicf(ψ,t) (MPa · h) for axes that were dehydrated at different relative humidities and temperatures. The results indicate that mechanical or physical stress would decrease with increasing relative humidity, whereas cumulative desiccation stress would increase. Cumulative desiccation stress of axes dried at 25°C was less than that at 16°C because axes dried slightly faster at the higher temperature under the same relative humidity. The ΔΨ/Δt and ∫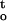Inline graphicf(ψ,t) were two interrelated parameters during desiccation. Desiccation tolerance of embryonic axes varied under different drying conditions (Fig. 3), and both ΔΨ/Δt and ∫Inline graphicf(ψ,t) were highly correlated with the critical water content of cocoa embryonic axes. Regression analysis shows that changes in ΔΨ/Δt and ∫Inline graphicf(ψ,t) accounted for 85% of the variation in desiccation tolerance for embryonic axes dried under different conditions (Table I). The maximum desiccation tolerance achieved with relative humidity of approximately 88% corresponded to a minimal value of combined desiccation stresses in embryonic axes (Fig. 7, A and B).

Figure 7.

Figure 7

Open in a new tab

A, Rate of dehydration (ΔΨ/Δt) and cumulative desiccation stress ∫Inline graphicf(ψ,t), of cocoa embryonic axes dried under various relative humidities at 16°C and 25°C. B, The influences of ΔΨ/Δt and ∫Inline graphicf(ψ,t) on desiccation tolerance of embryonic axes. The three-dimensional surface was drawn with fitted regression equation (see Table I). The maximum desiccation tolerance of embryonic axes (the valley of the three-dimensional surface) corresponded to relative humidity around approximately 88%, as indicated by the arrow in Figure 7A.

Table I.

Regression equations between the critical water content (CWC) of desiccation tolerance, rate of dehydration (ΔΨ/Δt), and cumulative desiccation stress ∫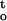Inline graphicf(ψ,t), for cocoa and ginkgo embryonic tissues

Species Regression Equation P Value R2
Cocoa CWC = 2.38 − 0.904log(ΔΨ/Δt) − 0.980log, ∫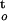Inline graphicf(ψ,t) <0.001 0.849
Ginkgo CWC = 0.091 − 0.45log(ΔΨ/Δt) − 0.000642, ∫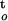Inline graphicf(ψ,t) <0.001 0.641
Open in a new tab

Modulation of Desiccation Tolerance of Ginkgo Embryos by Drying Rate

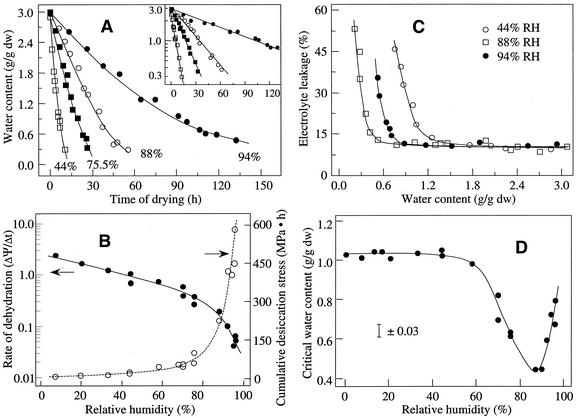
Cocoa is a tropical recalcitrant species. To make a more general conclusion, we have performed a similar quantitative analysis on the stress-time-response relationship for desiccation tolerance of temperate ginkgo embryos. Rate of dehydration, cumulative desiccation stress, and critical water content of ginkgo embryos under various relative humidities are shown in Figure 8. The result of correlation/regression analysis is presented in Table I. Changes in ΔΨ/Δt and ∫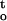Inline graphicf(ψ,t) accounted for 64% of the variation in desiccation tolerance for ginkgo embryos dried under different conditions, and the maximum desiccation tolerance at 88% relative humidity again corresponded to a minimal value of combined desiccation stresses in embryos.

Figure 8.

Figure 8

Open in a new tab

(A) Changes of water content in ginkgo embryos during desiccation at relative humidity 44%, 75.5%, 88%, and 94% at 16°C. Inset shows the first order plot for the calculation of rate constant of water loss. B, Rate of dehydration (ΔΨ/Δt) and cumulative desiccation stress ∫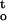Inline graphicf(ψ,t), of ginkgo embryos that were dried under different relative humidities. C, Representative plots between electrolyte leakage and water content shows the optimal drying condition at relative humidity 88%. D, Desiccation tolerance of ginkgo embryos that were dried under different relative humidities.

DISCUSSION

Effects of drying rate on desiccation tolerance of recalcitrant seeds are widely reported (Pammenter and Berjak, 1999). However, the mechanism by which drying rate affects desiccation tolerance has not been fully understood, and needs to be examined within a theoretic framework of physical and physicochemical stresses. Many studies reported that fast drying allowed recalcitrant seed tissues to survive to lower water (Farrant et al., 1985; Normah et al., 1986; Berjak et al., 1990, 1992, 1993; Pammenter et al., 1991, 1998, 1999; Pritchard, 1991; Berjak and Pammenter, 1997; Potts and Lumpkin, 1997; Kioko et al., 1998; Pritchard and Manger, 1998). The improvement in desiccation tolerance under fast drying conditions was generally attributed to the fact that recalcitrant seed tissues spent less time at the partially dried state. Under slow drying conditions, seed tissues spent a longer period of time at intermediate water contents, at which deleterious processes occur. Thus, fast drying was expected to minimize such deleterious processes (Pammenter and Berjak, 1999). However, this concept was called into question by our recent study, which discovered the existence of an optimal drying rate for cocoa embryonic axes (Liang and Sun, 2000). Both faster drying and slower drying were detrimental, and increased the sensitivity of embryonic axes to desiccation (Fig. 3). Identical result was also obtained with temperate ginkgo embryos (Fig. 8). The existence of an optimal drying rate suggested that desiccation damage could be minimized by studying the mechanism by which the drying rate affects desiccation tolerance of recalcitrant seed tissues. The present study have quantitatively examined the stress-time-response relationship for cocoa and ginkgo embryonic tissues during desiccation.

Desiccation damage to recalcitrant seed was a functional of two interrelated parameters: the rate and duration of dehydration. Embryonic tissues may be viewed as a viscoelastic system, and the mechanical or physical stress upon desiccation is proportional to rate of dehydration expressed by the negative value of the slope (ΔΨ/Δt) of the water potential/drying time plot (Figs. 1B and 2A). The effect of drying time was supposedly related to cumulative damages because of physicochemical effect or metabolic alterations upon desiccation. Although a direct quantification of cumulative physicochemical or metabolic stresses during desiccation proves to be difficult, such cumulative desiccation stress can be indirectly assessed, using a theoretic approach, through the integration of the tissue water potential/time function [i.e. ∫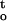Inline graphicf(ψ,t) during dehydration (Figs. 4–6 and 8). The response of recalcitrant cocoa and ginkgo embryonic tissues to the rate of dehydration was complex. Embryonic tissues were more sensitive to desiccation at both high and low rates of dehydration. Maximum desiccation tolerance was achieved with an optimal rate of dehydration at approximately 0.15 MPa h−1 for both species (Figs. 3 and 8). Desiccation tolerance of embryonic tissues under different conditions was highly correlated with the rate of dehydration (ΔΨ/Δt) and cumulative desiccation stress ∫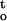Inline graphicf(ψ,t) , at both 16°C and 25°C (Figs. 7, 8, and Table I). These data suggest that different stress vectors interact to modulate desiccation tolerance or sensitivity of recalcitrant seeds. The interaction between dehydration rate and duration would affect physical and physicochemical processes that are associated with desiccation damage and desiccation tolerance. Different deleterious mechanisms were likely involved in desiccation damage under different dehydration conditions.

Cumulative desiccation stress was calculated by integrating the function ∫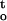Inline graphicf(ψ,t) from time zero to time t when seed tissues were dried to the critical water content. Cocoa and ginkgo embryonic tissues were fully hydrated before drying and water potential was 0 MPa at t = 0. Physicochemical stress would not start at water potential immediately below zero, but at water potential below a given threshold value (Sun and Liang, 2001). Such theoretic threshold water potential is unknown. Specific studies on enzyme function (Darbyshire and Steer, 1973) and plant growth (Kaufmann, 1968) under water stress reported significant metabolic disruptions and growth alterations when water potential decreased to −0.2 MPa (Kaufmann, 1968; Darbyshire and Steer, 1973). Therefore, it is conceivable that the onset of physicochemical stress during desiccation of recalcitrant seeds must occur at water potential higher than −0.2 MPa in plant tissues. Seed tissues can tolerate further desiccation without significant cellular damages or the loss of viability because of the presence of protective mechanisms (Sun and Liang, 2001). Because the critical water potential for cocoa and ginkgo embryonic tissues varied from −8 to −15 MPa under different drying conditions (Figs. 3, 8, and 9), the value of cumulative desiccation stress would not differ whether the function ∫Inline graphicf(ψ,t) was integrated from time zero (i.e. Ψ = 0 MPa) or from a given time t when Ψ decreased to the onset point of physico-chemical stress.

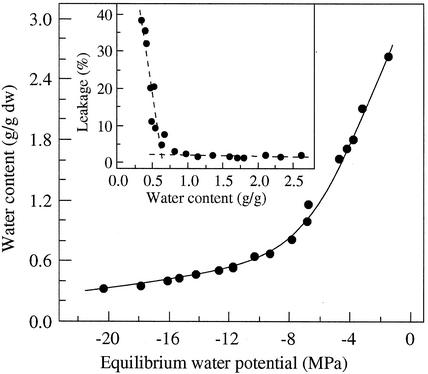
Figure 9.

Figure 9

Open in a new tab

Desorption isotherm of cocoa embryonic axes at 25°C. Axes were equilibrated over a series of water potential solutions at 25°C. Water content of axes were determined after the equilibrium was reached. Inset, Desiccation damage in axes after 9-d equilibrium as determined by electrolyte leakage method.

Physiological aging occurs in hydrated seed tissues and contributes to the gradual loss of seed viability during storage (Pammenter and Berjak, 1999). Desiccation tolerance of recalcitrant seeds and rehydrated orthodox seeds also decreases with storage time (Farrant et al., 1985, 1986; Sun et al., 1997; Tompsett and Pritchard, 1998), suggesting a possible association between physiological aging and the decrease of seed desiccation tolerance. Cumulative physicochemical effect of nonlethal water stress would undoubtedly enhance physiological aging. At the physicochemical level, the effect of nonlethal water stress on desiccation tolerance of recalcitrant seed tissues cannot be separated from its effect on physiological aging. Major biochemical deteriorations in physiological aging are quite similar to those observed in recalcitrant seeds upon desiccation (Li and Sun, 1999; Pammenter and Berjak, 1999).

In conclusion, the present study has quantitatively examined, using a theoretic thermodynamic approach, the effect of mechanical or physical stress and cumulative physicochemical stress on desiccation tolerance of cocoa embryonic axes under different dehydration conditions. These two stress vectors interacted to modulate desiccation tolerance or sensitivity of cocoa axes. High critical water contents under rapid drying conditions appeared to be mainly because of greater mechanical or physical stress, whereas high critical water content under very slow drying conditions was likely associated with the enormous increase in cumulative physicochemical stress that is coupled with metabolic alteration and damages in axes. These data provided valuable insight about the physiological basis of the optimal drying rate that promotes the maximum desiccation tolerance. Our analysis model on the basis of thermodynamic considerations will prove useful for the design of experiments that aim to elucidate biochemical and physiological mechanisms of desiccation tolerance.

MATERIALS AND METHODS

Plant Materials

Mature fruits of cocoa (Theobroma cacao) were harvested from a Malaysian plantation. Fruits were stored at 16°C temporarily, and normally used within 1 week. Under this storage condition, recalcitrant cocoa seeds (in the fruit) can be easily stored for more than 2 months without significant loss of seed viability and vigor (Li and Sun, 1999; Liang and Sun, 2000). Embryonic axes were excised from fresh fruits, and washed thoroughly in distilled water for 2 h before dehydration treatments.

Ginkgo (Ginkgo biloba) seeds (nuts) were collected from China and shipped to Singapore via courier services. Nuts were stored at 16°C and normally used within 2 months. Ginkgo seeds can be easily stored for more than 6 months under this condition. Uniform, middle-sized embryos (i.e. 1.0–1.2 cm long, average fresh weight of 30 mg) were chosen for experimental use. The dehydration treatment and determination of water potential for ginkgo embryos were similar to that for cocoa axes. We only described the experimental methods in details for cocoa embryonic axes in this paper.

Controlled Dehydration of Embryonic Axes

Samples of embryonic axes were dried in closed GA-7 culture vessels, where relative humidity conditions were maintained with salt solutions as described previously (Liang and Sun, 2000). Relative humidities used to achieve different drying rates varied from 6% to 97%, with accuracy of 0.3% at 25°C). Roughly 20 embryonic axes were dried over salt solution in each culture vessel, and 15 to 17 samples (vessels) were prepared for each relative humidity. Samples were regularly taken for the measurement of water content and for the assessment of desiccation damage. Water content of embryonic axes was gravimetrically determined after drying at 103°C for 24 h, and was expressed in grams water per grams dry weight. Desiccation damage was determined using the electrolyte leakage method and germination test (Sun and Leopold, 1993; Liang and Sun, 2000; Sun and Liang, 2001). Experiments were normally repeated two to four times for each relative humidity.

Determination of Axis Water Potential during Drying

Water potential in embryonic axes was derived from water content according to sorption isotherms (Sun and Gouk, 1999). Samples of approximately 20 embryonic axes were equilibrated over a series of salt solutions with water potential ranging from −22 to −1.3 MPa in closed containers at 16°C ± 0.5°C and 25°C ± 1.0°C. Upon equilibrium, water contents of axis samples were determined gravimetrically. Figure 9 shows the relationship between water potential and the equilibrium water content of cocoa embryonic axes at 25°C. Similar data for cocoa axes at 16°C and ginkgo embryos at 16°C was obtained (not shown). Derived mathematical relationships between water content and water potential were used to calculate water potential of embryonic axes during drying. This method was preferred to several commonly used instrumental techniques because the later techniques were either not suitable for low moisture systems or did not allow rapid monitoring of water potential change in embryonic axes during drying. Psychrometric and hydrometric methods is suitable only for plant tissues of high water contents, and the nominal range of measurement is limited from 0 to −6.0 MPa for those two methods. Most recalcitrant seed tissues can survive far below −6.0 MPa. Even if the Richards thermocouple is to be used, it extends only to −25 MPa and the accuracy decreases to −0.1 MPa at −10 MPa (Decagon Devices Inc., Pullman, WA), corresponding to a relative humidity of approximately 84% at 25°C only. At low water content, the equilibrium may take several hours to achieve. Methods for the determination of plant tissue water potential were reviewed by Sun and Gouk (1999). The mathematical analysis of sorption data was performed using the macro functions developed by the author (W.Q.S.) and inserted into the software “Igor” (WaveMetrics, Lake Oswego, OR). Marco programs are available free of charge from the author.

Footnotes

1

This work was supported by the National University of Singapore (research grant nos. R–154–000–032–112 and R–154–000–074–112 to W.Q.S.).

Article, publication date, and citation information can be found at www.plantphysiol.org/cgi/doi/10.1104/pp.010616.

LITERATURE CITED

  1. Berjak P, Farrant JM, Mycock DJ, Pammenter NW. Recalcitrant (homoiohydrous) seeds: the enigma of their desiccation sensitivity. Seed Sci Technol. 1990;18:297–310. [Google Scholar]
  2. Berjak P, Pammenter NW. Progress in the understanding and manipulation of desiccation-sensitive (recalcitrant) seeds. In: Ellis RH, Black M, Murdoch AJ, Hong TD, editors. Basic and Applied Aspects of Seed Biology. Dordrecht, The Netherlands: Kluwer Academic Publishers; 1997. pp. 689–703. [Google Scholar]
  3. Berjak P, Pammenter NW, Vertucci CW. Homoiohydrous (recalcitrant) seeds: development status, desiccation sensitivity and the state of water in axes of Landolphia kirkii Dyer. Planta. 1992;186:249–261. doi: 10.1007/BF00196255. [DOI] [PubMed] [Google Scholar]
  4. Berjak P, Vertucci CW, Pammenter NW. Effect of developmental status and dehydration rate on characteristics of water and desiccation-sensitivity in recalcitrant seeds of Camellia sinensis. Seed Sci Res. 1993;3:155–166. [Google Scholar]
  5. Bradford KJ. A water relation analysis of seed germination rates. Plant Physiol. 1990;94:840–849. doi: 10.1104/pp.94.2.840. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bradford KJ. Water relations in seed germination. In: Kigel J, Galili G, editors. Seed Development and Germination. New York: Marcel Dekker, Inc.; 1995. pp. 351–396. [Google Scholar]
  7. Bradford KJ. Population-based models describing seed dormancy behavior: implications for experimental design and interpretation. In: Lang GA, editor. Plant Dormancy: Physiology, Biochemistry and Molecular Biology. Wallingford, UK: CAB International; 1996. pp. 313–39. [Google Scholar]
  8. Bradford KJ. The hydrotime concept in seed germination and dormancy. In: Ellis RH, Black M, Murdoch AJ, Hong TD, editors. Basic and Applied Aspects of Seed Biology. Dordrecht, The Netherlands: Kluwer Academic Publishers; 1997. pp. 349–360. [Google Scholar]
  9. Bradford KJ, Somasco OA. Water relations of lettuce seed thermoinhibition: I. Priming and endosperm effects on base water potential. Seed Sci Res. 1994;4:1–10. [Google Scholar]
  10. Côme D, Corbineau E. Metabolic damage related to desiccation sensitivity. In: Quédraogo A-S, Poulsen K, Stubsgaard F, editors. Intermediate/Recalcitrant Tropical Forest Tree Seeds. International Plant Genetic Resources Institute, Rome. 1996. pp. 83–97. [Google Scholar]
  11. Darbyshire D, Steer BT. Dehydration of macromolecules: I. Effects of dehydration-rehydration on indoleacetic acid oxidase, ribonucleas, ribulose diphosphate carboxylase and aldolase. Aust J Biol Sci. 1973;26:591–604. [Google Scholar]
  12. Farrant JM, Berjak P, Pammenter NW. The effect of drying rate on viability retention of recalcitrant propagules of Avicennia marina. S Afr J Bot. 1985;51:432–438. [Google Scholar]
  13. Farrant JM, Berjak P, Pammenter NW. Studies on the development of the desiccation-sensitive (recalcitrant) seeds of Avicennia marina (Forssk.) Vierh: the acquisition of germinability and response to storage and dehydration. Ann Bot. 1993;71:405–410. [Google Scholar]
  14. Farrant JM, Pammenter NW, Berjak P. The increasing desiccation sensitivity of recalcitrant Avicennia marina seed with storage time. Physiol Plant. 1986;67:291–298. [Google Scholar]
  15. Fu JR, Zhang BZ, Wang XP, Qiao YZ, Huang XL. Physiological studies on desiccation, wet storage and cryopreservation of recalcitrant seeds of three fruit species and their excised embryonic axes. Seed Sci Technol. 1990;18:743–754. [Google Scholar]
  16. Gummerson RJ. The effect of constant temperatures and osmotic potentials on the germination of sugar beet. J Exp Bot. 1986;37:729–741. [Google Scholar]
  17. Kaufmann MR. Water relations of pine seedlings in relation to root and shoot growth. Plant Physiol. 1968;43:281–288. doi: 10.1104/pp.43.2.281. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Kebreab E, Murdoch AJ. Modelling the effect of water stress and temperature on germination rate of Orobanche aegyptiaca seeds. J Exp Bot. 1999;50:655–664. [Google Scholar]
  19. Kebreab E, Murdoch AJ. The effect of water stress on the temperature range for germination of Orobanche aegyptiaca seeds. Seed Sci Res. 2000;10:127–133. [Google Scholar]
  20. Kioko J, Berjak P, Pammenter NW, Watt PM, Wesley-Smith J. Desiccation and cryopreservation of embryonic axes of Trichilia dregeana Sond. Cryo-Lett. 1998;19:15–26. [Google Scholar]
  21. Li CR, Sun WQ. Desiccation sensitivity and activities of free radical-scavenging enzymes in recalcitrant Theobroma cacao seeds. Seed Sci Res. 1999;9:209–217. [Google Scholar]
  22. Li X, Feng Y, Boersma L. Activation energy as a measure of plant response to temperature and water stresses. Ann Bot. 1991;68:151–157. [Google Scholar]
  23. Liang YH, Sun WQ. Desiccation tolerance of recalcitrant Theobroma cacao embryonic axes: the optimal drying rate and its physiological basis. J Exp Bot. 2000;51:1911–1919. doi: 10.1093/jexbot/51.352.1911. [DOI] [PubMed] [Google Scholar]
  24. Normah MN, Chin HF, Hor YL. Desiccation and cryopreservation of embryonic axes of Hevea brasiliensis Muell-Arg. Pertanika. 1986;9:299–303. [Google Scholar]
  25. Pammenter NW, Berjak P. A review of recalcitrant seed physiology in relation to desiccation-tolerance mechanisms. Seed Sci Res. 1999;9:13–37. [Google Scholar]
  26. Pammenter NW, Berjak P, Walters C. The effect of drying rate, and processes leading to viability loss in recalcitrant seeds. In: Marzalina M, Khoo KC, Jayanti N, Tsan FY, Krishnapillay B, editors. Recalcitrant Seeds (Proceedings of International Union of Forest Research Organizations Seed Symposium 1998). Kuala Lumpur: Forest Research Institute Malaysia; 1999. pp. 14–24. [Google Scholar]
  27. Pammenter NW, Greggains V, Kioko JI, Wesley-Smith J, Berjak P, Finch-Savage WE. Effects of differential drying rates on viability retention of recalcitrant seeds of Ekebergia capensis. Seed Sci Res. 1998;8:463–471. [Google Scholar]
  28. Pammenter NW, Vertucci CW, Berjak P. Homeohydrous (recalcitrant) seeds: dehydration, the state of water and viability characteristics in Landolphia kirkii. Plant Physiol. 1991;96:1093–1098. doi: 10.1104/pp.96.4.1093. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Potts SE, Lumpkin TA. Cryopreservation of Wasabia spp. seeds. Cryo-Lett. 1997;18:185–190. [Google Scholar]
  30. Pritchard HW. Water potential and embryonic axis viability in recalcitrant seeds of Quercus rubra. Ann Bot. 1991;67:43–49. [Google Scholar]
  31. Pritchard HW, Manger KR. A calorimetric perspective on cumulative water stress during preservation procedures with recalcitrant seeds of Quercus robur L. Cryo-Lett. 1998;19(S):23–30. [Google Scholar]
  32. Roberts EH, Ellis RH. Water and seed survival. Ann Bot. 1989;63:39–52. [Google Scholar]
  33. Sun WQ, Gouk SS. Preferred parameters and methods for studying moisture content of recalcitrant seeds. In: Marzalina M, Khoo KC, Jayanti N, Tsan FY, Krishnapillay B, editors. Recalcitrant Seeds (Proceedings of International Union of Forest Research Organizations Seed Symposium). Kuala Lumpur: Forest Research Institute Malaysia; 1999. pp. 404–430. [Google Scholar]
  34. Sun WQ, Koh DCK, Ong CM. Correlation of modified water sorption properties with the decline of storage stability of osmotically primed seeds of Vigna radiata (L.) Wilczek. Seed Sci Res. 1997;7:391–397. [Google Scholar]
  35. Sun WQ, Leopold AC. Acquisition of desiccation tolerance in soybeans. Physiol Plant. 1993;87:403–409. [Google Scholar]
  36. Sun WQ, Liang YH. Discrete levels of desiccation sensitivity in various seeds as determined by the equilibrium dehydration method. Seed Sci Res. 2001;11:317–323. [Google Scholar]
  37. Tompsett PB, Pritchard HW. Water status changes during development in relation to the germination and desiccation tolerance of Aesculus hippocastanum L. seed. Ann Bot. 1993;71:107–116. [Google Scholar]
  38. Tompsett PB, Pritchard HW. The effect of chilling and moisture status on the germination, desiccation tolerance and longevity of Aesculus hippocastanum L. seed. Ann Bot. 1998;82:249–261. [Google Scholar]
  39. Vertucci CW, Crane J, Porter RA, Oelke EA. Physical properties of water in Zizania embryos in relation to maturity, water content and temperature. Seed Sci Res. 1994;4:211–224. [Google Scholar]
  40. Vertucci CW, Crane J, Porter RA, Oelke EA. Survival of Zizania embryos in relation to water content, temperature and maturity status. Seed Sci Res. 1995;5:31–40. [Google Scholar]
  41. Vertucci CW, Roos EE. Theoretic basis of protocols for seed storage. Plant Physiol. 1990;94:1019–1023. doi: 10.1104/pp.94.3.1019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Vertucci CW, Roos EE. Theoretic basis of protocols for seed storage: II. The influence of temperature on optimal moisture levels. Seed Sci Res. 1993;3:201–213. [Google Scholar]

Articles from Plant Physiology are provided here courtesy of Oxford University Press

RESOURCES