Observation of the cascaded atomic-to-global length scales driving protein motion

Abstract

Model studies of the ligand photodissociation process of carboxymyoglobin have been conducted by using amplified few-cycle laser pulses short enough in duration (<10 fs) to capture the phase of the induced nuclear motions. The reaction-driven modes are observed directly in real time and depict the pathway by which energy liberated in the localized reaction site is efficiently channeled to functionally relevant mesoscale motions of the protein.

Principles of chemistry and biology merge at the active or receptor sites of proteins. The initial reaction forces that are harnessed in biological processes are subjected to atomic-length scale fluctuations that ultimately must manifest their effect over the mesoscale dimensions of the biological complex. In one extreme, the system is subject to quantum effects, and in the other limit there are enough degrees of freedom that a continuum or classical description is appropriate. Nature seamlessly bridges the quantum and classical limits of force transduction. Exactly how biological systems transcend the quantum to continuum limits of mechanics is an open issue. Given the enormous number of superfluous degrees of freedom in biological molecules, there must exist efficient pathways by which conformational potential energy is transmitted from a localized chemical reaction site to the relevant functional degrees of freedom. The process by which this energy channeling occurs is one of the central mysteries in understanding biomechanics. Here we observe the photodissociation process of carboxymyoglobin (MbCO) using visible, few-cycle-duration light pulses to probe very fast nuclear motions in this system. The phase and amplitude of the reaction-driven modes give direct insight into the pathway by which initially localized reaction forces become spatially distributed and ultimately couple to the protein's functionally relevant motions.

Myoglobin serves as a model system for the tertiary protein motions that form the basis for the molecular cooperativity exhibited by hemoglobin in the transport of oxygen. In the oxymyoglobin tertiary structure, the iron porphyrin plane defining the oxygen-binding site is planar. The deoxymyoglobin (deoxyMb) tertiary structure (pentavalent iron) is distinctly different. The iron is displaced 0.3 Å to the proximal side from the plane, the heme porphyrin puckers slightly, and there are long-range correlated motions of the surrounding globin (1–3). The most pronounced motion involves the E-F helix, in closest contact with the iron through the proximal histidine, and defines the primary allosteric motions controlling molecular cooperativity. The force for this motion is thought to be derived from the iron out-of-plane displacement and heme puckering: the so-called heme-doming coordinate. This before-and-after picture defines a transition-state process in which the initially localized reaction forces of the Fe—ligand (O₂) bond seem to act normal to the heme plane and ultimately displace the E-F helix and associated helices. How do these initially localized reaction forces extend their effect over the requisite length scales? The initial events of bond dissociation, for example, must involve fluctuations on the angstrom-length scale yet couple out to mesoscale dimensions to affect protein interactions.

To explore the issue discussed above, it is essential to be able to probe the fastest, most localized nuclear motions coupled to the Fe—ligand reaction coordinate. To this end, a laser source has been developed based on noncollinear optical parametric amplification (4) in combination with a deformable mirror-adaptive optic approach to generate tunable optical pulses of <10 fs on target (5). MbCO was chosen for these studies over oxymyoglobin because the quantum yield for photodissociation of the Fe—CO bond is unity, and complications from ligand recombination are eliminated (6, 7). This feature turned out to be particularly important in extending the time base to improve the accuracy in the frequency resolution of the observed vibrational coherences. Equally important, the ligand photodissociation is known to occur on very fast time scales. Within a time-domain experiment, in order for nuclear modulations of the optical response to be associated with the photoinduced reaction coordinate the reaction process must occur on time scales comparable or faster than the period of the particular nuclear mode. Previous studies have reported that Fe—ligand photodissociation occurs within 50 fs (8), although evidence for longer-lived electronic metastable states (300–400 fs) along the relaxation pathway to the ground deoxyMb product state (7–13) has made consensus on the exact dynamics of the bond-breaking event and relaxation pathway open to debate. Recent femtosecond coherent spectroscopy studies of FeNO and MbCO (6, 7, 14, 15) using 40-fs pulses have suggested that this reaction is capable of impulsively driving modes. The observed nuclear coherences within this interpretation place the bond-breaking event to occur on the 100-fs time scale or faster (6), in accordance with the early estimates. By using very short pulses (<10 fs), the present study has access to all relevant reaction modes and enough frequency resolution for the high-frequency modes to remove the ambiguity in identifying reaction-driven modes.

Methods

For these very fast time-resolution studies, we used the broadband (>70-nm) output of a noncollinear optical parametric amplifier pumped by an amplified short-pulse (≈150 fs) Ti:Sapphire-based laser system as described (5). This system produces sub-10-fs visible pulses at 1 kHz with an average power of 5–7 mW. In these experiments, typically the pump-pulse energy was 0.5 μJ, and the probe energy was 0.1 μJ, with a beam diameter of 200 μm. The optical parametric amplifier was tuned for absorption in the Q band of myoglobin with the spectrum centered at 525 nm. This high time resolution enables the detailed observation of the transition of the molecule from ligated MbCO to deligated deoxyMb + CO. By exciting in the Q band, vibrational information may be discerned that is distinct from that obtained through Soret-band excitation (16, 17). In the work presented in this article, we have spectrally resolved the probe within a 2-nm bandwidth at 538 nm. A probe wavelength dependence was conducted between 520 and 540 nm, and the signal dependence was found to be wavelength-independent in this range. The best signal-to-noise ratio was found for probe wavelengths centered at 538 nm and enabled a full analysis of the time traces out to 7 ps for highest accuracy to the observed frequency modulation. In general, pulses of this duration should resolve these oscillations with energies as high as 1,500 cm⁻¹, and high-frequency oscillations are observed in experiments with both myoglobin and rhodamine 6G. To further confirm the short-pulse nature of the experiment, pump-probe cross correlations at the sample position were measured to be 7–8 fs. High pulse quality is also important. This pulse duration is within 30% of the transform limit for the spectral profiles of these pulses. The specific form of the phase profile of the pulses was determined by spectral analysis (5) and a χ⁽³⁾ frequency-resolved gating method. There are small residual phase differences on the spectral wings of the pulse from the transform limit that lead to a small shoulder on the pulse profile. The shoulder is only 10% in amplitude relative to the most intense part of the pulse and is not significant with respect to the inferred relative amplitudes of the driven nuclear modes.

Horse-heart myoglobin and cytochrome c (cyt c) were purchased from Sigma–Aldrich, dissolved in 0.2 M Tris buffer (pH 7.0), and used as described (18, 19). The final sample concentrations gave an OD₅₃₀ of 1. The deoxyMb and cyt c samples were flushed with nitrogen gas overnight and reduced with a 2-fold excess of sodium dithionite solution. MbCO samples were flushed with CO gas for 2 h and then reduced in the same fashion. The MbCO samples were then kept under a CO environment throughout the experiment, whereas a nitrogen environment was used for the deoxyMb and ferrous cyt c samples. The integrity of each sample was verified via its UV-visible spectrum. A peristaltic pump flowed the sample through a gas-tight cell at a fast enough rate to ensure a new sample for each laser shot. The optical path length of the cell was 100 μm to reduce pulse broadening in the sample.

Results and Discussion

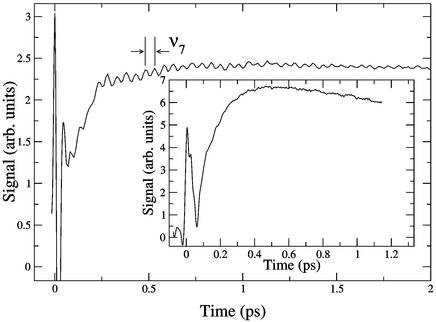
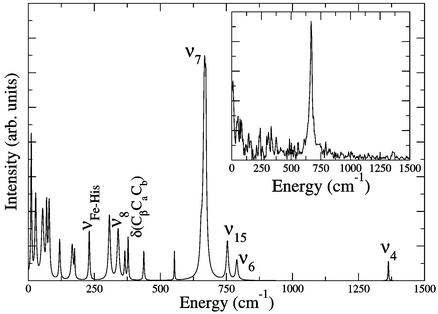
A plot of typical raw pump-probe data are shown in Fig. 1. The time response of the protein shows an initially large, fast-changing signal near t = 0 that is due to electronic polarization effects in the sample. The most important information is subsequent to this feature, where very pronounced oscillations in the data are observed. This signal modulation is due to the excitation of vibrational modes of the heme porphyrin that is the absorption center for the light pulse. The identity of the nuclear motions can be determined from the frequency of the oscillations and comparison to previous isotope studies (20) used to assign the modes of this system. These results are shown in Fig. 2, where linear predictive singular value decomposition (LPSVD) (6, 14, 21, 22) is used to fit the data. As seen in Fig. 1, there is one very pronounced feature that is clearly captured by the Fourier transform of the raw data shown in Fig. 2 Inset for comparison to the LPSVD fit. Although some noise peaks remain after the LPSVD analysis, many signal peaks correspond to peaks observed in equilibrium resonance Raman spectra of deoxyMb (20, 23). The most strongly excited mode observed in this experiment is the symmetric in-plane heme-breathing mode, designated ν₇. There are two possible explanations for this observed vibrational modulation of the signal. The vibrational mode may be excited either by a resonance Raman process (field-driven) involving the ground state of the nascent molecule or during the displacements along the photoinduced reaction coordinate (reaction-driven) and reflects a product state. These two mechanisms have been discussed at length in this context (6, 7). Here the use of MbCO in these studies is important, because it was possible to extend the time scans up to 7 ps without complications from geminate recombination of the ligand. The accuracy of the frequency resolution is only limited by the lifetime of the excited mode and signal-to-noise considerations. Equilibrium resonance Raman spectra place the mode at 678 cm⁻¹ in MbCO, whereas the LPSVD analysis of the time trace indicates that this mode is significantly red-shifted to 667 ± 4 cm⁻¹ in excellent agreement with the observed frequency for excited deoxyMb (24). This difference in frequency supports the assignment of the observed ν₇ mode to reaction-driven nuclear motion in deligated myoglobin not resonance Raman pump-excited ground-state motion of MbCO. This result is supported further by the lack of observed ν₇ oscillations in deoxyMb under identical conditions.

Figure 1.

Raw MbCO data detected at 538 nm (2-nm detection bandwidth). There is an obvious principle oscillation with a period of 50 fs clearly visible in the data. (Inset) Cyt c data detected at 523 nm. No vibrational coherences are observed over the same wavelength range spanning the Q band for the protein.

Figure 2.

The spectrum of the LPSVD fit to the background-subtracted MbCO data showing strong oscillations at the ring-breathing mode ν₇. (Inset) Fourier transform of the MbCO data.

As an additional control, studies of cyt c, another heme protein, with a methionine ligand instead of CO were conducted. Cyt c has very similar optical properties to MbCO and also demonstrates a high quantum yield for photodissociation (≥80%) of the methionine group (18). The Fe—Met bond energy is lower than the MbCO bond (Fe—CO) (17), and this difference should manifest itself as a phase shift and/or change in modulation amplitude for a reaction-driven process. As shown in Fig. 1 Inset, negligible oscillation of ν₇ is observed for cyt c and thus supports the assignment to a reaction-driven mode. To elaborate further, this difference in amplitude modulation can be understood by considering the time scales for the bond dissociation and motion onto the pentavalent iron-product surface in the two cases. To observe coherent oscillations under pulsed-excitation conditions, the perturbation to a system of oscillators must interact with the system for a time period of duration less than the fundamental period of the vibration. The smaller reaction force (Fe—ligand bond energy) and much larger mass of the methionine group of cyt c in relation to the CO of MbCO translates into much slower motion along the dissociative pathway. Although optical excitation projects the system onto a repulsive or dissociative excited state, the initial inertial motion of the ligand is governed by the ground-state potential. By using a half-period of the Fe—ligand as a gauge of the relative motion of the ligand along the reaction pathway (65-fs period for Fe—CO and 97-fs period for Fe—Met; ref. 17), it should take approximately twice as long for the system to sample the pentavalent Fe-product state in cyt c as it would for MbCO, and thus the development of the reaction forces is too slow to impulsively drive the ν₇ mode. This discussion focuses on the differences in the Fe-ligation coordinate. The time evolution of the excited states onto the pentavalent product surface is also determined by the degree of nuclear wave function overlap or Franck–Condon factors that determine the transition probability between the two electronic manifolds. It is possible that structurally dependent differences in Franck–Condon factors effectively slow the rate of crossing in cyt c relative to MbCO as well. In either case, the conclusion is the same. The slower photodissociation process in cyt c is too slow to impulsively drive ν₇. Had the excitation mechanism involved a field-driven process, we should have observed comparable modulation of the signal at the known frequency of the ν₇ of cyt c. We note in passing that the frequency of the corresponding ν₇ mode in the pentavalent state of photoexcited cyt c is not well defined, but studies of model compounds place the frequency in the 680- to 722-cm⁻¹ range (25), i.e., similar to deoxyMb. The main point is that the absence of vibrational modulation in the case of the cyt c control study supports the assignment of the vibrational coherences of MbCO to reaction-driven processes as suggested previously (6, 7, 14).

The ring antisymmetric breathing mode, designated ν₄, is also observed in MbCO data at 1,363 cm⁻¹, as shown in Fig. 2, and is also significantly red-shifted from the equilibrium value in MbCO (1,373 cm⁻¹) to the deoxyMb value, 1,355 cm⁻¹ (17, 23). Recently, elegant studies of IR emission from MbCO single crystals under pulsed-excitation conditions also observed high-frequency modes close to ν₄ (although not ν₇, because frequencies <900 cm⁻¹ were too strongly attenuated by medium absorption) and suggested that it may be a reaction-driven process (26). By fully resolving the frequency shift, this assignment can now be made. The impulsive excitation of the ν₄ mode, albeit with much smaller amplitude than ν₇, indicates that the Fe—CO bond dissociation and reaction forces develop on time scales <25 fs, as a refinement to previous estimates. Very fast bond dissociation is consistent with recent work demonstrating the appearance of the reaction-driven Fe—His mode with no apparent phase delay (6). It should be noted that the observation of both ν₄ and ν₇ modes illustrates that the actual transition state for the Fe—ligand reaction coordinate involves a component of nuclear motion in the plane of the heme consistent with the displacements found in ν₄ and ν₇ oscillations. In retrospect, this observation should not be too surprising. The deformation of the porphyrin ring with heme doming to the fully relaxed deoxyMb structure involves displacements as large as 0.1 Å (1) of the heavy atoms bonded to the iron. In order for the iron to move out of plane, the modes ν₄ and ν₇ also must be displaced in the process. During the reactive crossing, the system is displaced further from equilibrium, and the heme-doming coordinate would involve a superposition of modes in this nonstationary state that define this motion. Because the system is displaced further from equilibrium than average thermal fluctuations, the anharmonic coupling between these modes will be greater than that which could be inferred from studies of equilibrium structures.

To investigate the connection between in-plane oscillations of the postligation heme and ultimate channeling to global protein-conformation changes, we have examined the temporal dependence of the phase of the reaction-driven modes. This information is derived from the instantaneous frequency (IF) of ν₇ by applying a Gaussian filter to the portion of the Fourier spectrum corresponding to ν₇, inverse Fourier-transforming the filtered data to obtain a time trace [TT(t)] with time-dependent phase f(t) and real amplitude A(t),

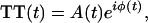1

and calculating the IF (t) defined as (27)

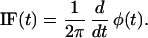2

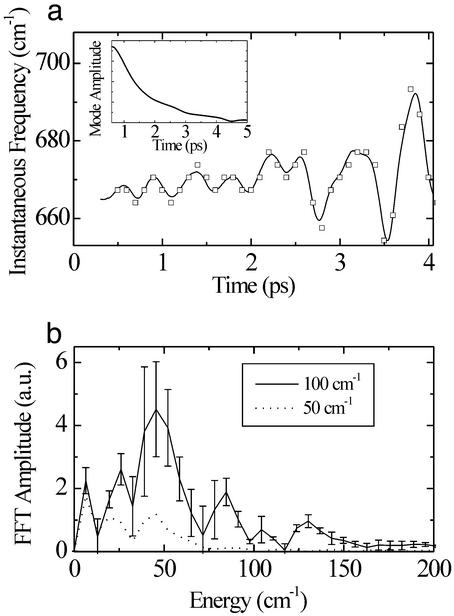
The time-dependent frequency of time-domain data has also been examined through the use of a sliding Fourier window technique (28, 29). Although an IF analysis provides similar information to the sliding-window technique, it is not inherently limited in resolution. It should be noted that frequency modulation of a given mode results in side bands in conventional frequency-domain measurements, but these side bands are generally too small to be observed above background (28). Most important, such studies are incapable of accessing information on nuclear motions that are far from equilibrium, where anharmonic coupling between modes is more pronounced, and of direct relevance to chemical reactions. The sensitivity of vibrational coherence spectroscopy toward this information is shown in Fig. 3, where ν₇ is found to have strong oscillations in the IF over ≈4 ps after photodissociation. A Fourier transform of the IF is shown in Fig. 1 Inset. Although the width of the Fourier spectrum of the IF will not exceed the width of the window used to filter the time-domain data, the peak frequencies do not depend significantly on the filter location or width as shown by comparing filter bandwidths of 50 and 100 cm⁻¹. For the 100-cm⁻¹ window, this plot shows oscillations around 25, 48, 84, and 134 cm⁻¹, with the higher frequency peaks (≥50 cm⁻¹) possibly corresponding to a fundamental oscillation and overtones that are consistent with measurements over longer time domains and discussion of anharmonic coupling between these modes (6, 14, 15). The resolution of the frequency modulation is fundamentally limited by the signal-to-noise ratio of the experiment and the decay time of the ν₇ mode (Fig. 3a Inset). This feature limits the reliable time base to ≈4 ps as shown and introduces the largest relative uncertainty to the lowest frequency modulations after conducting the Fourier transform from the time domain to the frequency domain. An error analysis was conducted by determining the accuracy limits of the IF analysis with respect to the signal-to-noise ratio of the time-domain scan. The error bars are shown in the figure for the various peaks to explicitly show the degree of confidence in the spectral positions. It is possible for mode-beating to modulate the IF, and the 84-cm⁻¹ peak may be due to mode-beating of ν₇ with another consistently observed mode at 753 cm⁻¹. However, no other modes with the corresponding frequency spacing exist within the bandwidth of the 50 cm⁻¹ (full-width at half-maximum) filter, according to resonance Raman spectra of MbCO and LPSVD fits of the raw time data (20, 30). Therefore, the peaks at 25 and 48 cm⁻¹ are the result of modulation of the ν₇ mode frequency. These energies match peaks measured in Raman and longer-time pump-probe measurements of MbCO; and generally, the doming mode and lower frequency, longer-range motions involving the isopropyl side chains are assigned to these peaks (6, 14, 31). The lowest frequency modulation is very near resonance, with recent observations of anisotropic displacements of the surrounding globin after ligand dissociation (32, 33) and frequency components derived from a modal analysis of the protein structure (34, 35). The coupling between the high-frequency modes and the more extended modes involving the entire heme moiety provide a conduit for transducing the reaction forces to the correct length scale to drive functionally relevant protein motions. The exact degree of coupling between the heme porphyrin moiety and the surrounding protein is difficult to determine within the present signal-to-noise limitations. More systematic studies of the dependence on the surrounding protein on this low frequency part of the frequency modulation are needed along with the prerequisite improvement in sensitivity. This part of the spectrum, however, is very congested and mode-specific coupling related to the details of the protein structure will likely be difficult to discern. Within the present context, the observation of frequency modulation of the ν₇ mode, coincident with the heme-doming and lower frequencies, directly depicts the mode–mode coupling and the projection of reaction forces over longer length scales of motion.

Figure 3.

(a) The IF generated with a 100-cm⁻¹ filtering window (solid line). The results of the sliding window analysis are shown by the square points in the graph for comparison. The y value of each point is the peak frequency of the Fourier transform of a 200-fs full-width half-maximum Gaussian window centered at the time value of the point. (Inset) Decay in the mode amplitude. (b) Fourier transform of the IF when the IF was generated with 100- and 50-cm⁻¹ windows.

Conclusions

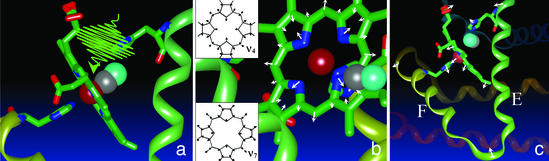
The picture that is emerging is that heme proteins represent a strongly coupled network of nuclear resonances as shown schematically in Fig. 4. The high-frequency in-plane motions (ν₄, ν₇) are coupled to out-of-plane motions along the heme normal that are related to the heme doming. Motion along this latter coordinate is generally considered to be responsible for driving functionally relevant protein motions on a global scale. The observed coupling between these different types of motions illustrates that the transition state for ligand dissociation is more complex than simple displacement of the iron out of the heme plane. This nonstationary state is better represented as a superposition of different modes that involve various degrees of displacement during the motion of the iron out of plane. One may consider the instantaneous focus of the reaction to involve electron redistribution between the iron and the ligand at some critical point in the nuclear configuration phase space; however, the subsequent motions in response to this force would be a superposition of modes that rapidly spatially redistribute this initially localized event. In the present case of photoinduced dissociation, the initial rate of passage to the deoxyMb electronic surface is fast enough to cast out the reaction-driven motions involving the in-plane (ν₄, ν₇) modes. These displacements in turn are coupled to motions along the doming coordinate (40–50 cm⁻¹) and subsequently to spatially extended modes (centered at 25 cm⁻¹) involving the entire heme porphyrin moiety embedded in the protein matrix. These modes are far from their equilibrium or relaxed nuclear configurations as evidenced by the mode mixing and are able to couple to the spatially extended modes of the surrounding globin. For example, the oxy- to deoxy-protein structural changes likewise can be described as a superposition of collective modes involving segmental fluctuations of the E-F and other key helices that lie within the range of 5–25 cm⁻¹ (36, 37). These more-global protein motions are near resonance with the lowest frequency motions at the heme-binding site and should strongly couple, as suggested by the lowest frequency modulation of the ν₇ mode. In this manner, the reaction forces at the binding site become channeled very efficiently into the spatially extended motions central to protein functions.

Figure 4.

Energy channeling in MbCO. (a) A photon breaks the ligand bond. (b) The Fe—CO bond breaks, and the repulsive iron motion couples to the ring-breathing modes, exciting the modes. (Insets) Details of the ν₇ and ν₄ modes (38). (c) The displacement of the breathing modes is part of a superposition of modes that enable the iron to move out of plane and the heme to dome (motions are exaggerated). The doming motion is then coupled to lower-frequency skeletal modes and ultimately to mesoscale motions of the E and F helices (protein motions depicted after ref. 1). These panels schematically show the reaction-driven modes and cascade to different length scales of motion along the reaction coordinate.

Abbreviations

MbCO

carboxymyoglobin

deoxyMb

deoxymyoglobin

cyt c

cytochrome c

LPSVD

linear predictive singular value decomposition

IF

instantaneous frequency