The role of side-chain interactions in the early steps of aggregation: Molecular dynamics simulations of an amyloid-forming peptide from the yeast prion Sup35

Abstract

Understanding the early steps of aggregation at atomic detail might be crucial for the rational design of therapeutics preventing diseases associated with amyloid deposits. In this paper, aggregation of the heptapeptide GNNQQNY, from the N-terminal prion-determining domain of the yeast protein Sup35, was studied by 20 molecular dynamics runs for a total simulation time of 20 μs. The simulations generate in-register parallel packing of GNNQQNY β-strands that is consistent with x-ray diffraction and Fourier transform infrared data. The statistically preferred aggregation pathway does not correspond to a purely downhill profile of the energy surface because of the presence of enthalpic barriers that originate from out-of-register interactions. The parallel β-sheet arrangement is favored over the antiparallel because of side-chain contacts; in particular, stacking interactions of the tyrosine rings and hydrogen bonds between amide groups. No ordered aggregation was found in control simulations with the mutant sequence SQNGNQQRG in accord with experimental data and the strong sequence dependence of aggregation.

Amyloid fibrils are highly ordered protein aggregates associated with severe human disorders including Alzheimer's disease, type II diabetes, systemic amyloidosis, and transmissible spongiform encephalopathies (1, 2). The soluble precursors of the amyloidogenic proteins do not share any sequence homology or common fold. However, x-ray diffraction data indicate a cross-β structure for all amyloid fibrils (3, 4). These findings suggest that key steps in the aggregation process may be common to all amyloidogenic proteins. Despite the medical relevance of amyloidosis, many important questions about the formation of ordered aggregates remain unanswered. What energetic contributions stabilize the species formed early in the aggregation process? In particular, what is the role of side-chain interactions and what are the most favorable side-chain arrangements? How sensitive is amyloid formation to small changes in the amino acid sequence?

There have been several lattice studies on aggregation in proteins. These simplified models have allowed for the investigation of the relevance of aggregation on the folding process (5) and how interaction potentials affect the properties of aggregation-prone proteins (6). Harrison et al. (7) have shown that less stable proteins have a greater chance of assuming alternative native states as multimers. Molecular dynamics (MD) simulations of aggregation have been performed by using a three-bead backbone and a single-bead side-chain model (8). Although this simplified model has allowed the simulation of the competition between folding and aggregation for two four-helix bundles, it is probably not possible to extract detailed information on energetics and sequence dependence. Recently, MD simulations of atomic models of amyloidogenic peptides have been performed with an implicit treatment of the solvent (9) and explicit water molecules (10, 11). In the former, the role of complex environments on the stabilization of intermolecular hydrogen bonds was investigated (9). The simulations of oligomers of Alzheimer's amyloid peptides in explicit water indicate that Aβ_16–22 aggregates with an antiparallel β-sheet orientation in agreement with solid state NMR data and that Aβ_16–35 cannot form linear parallel β-sheets because of unfavorable polar contacts (11).

The heptapeptide GNNQQNY from the yeast prion Sup35 (residues 7–13) displays the same amyloid properties as full-length Sup35, including cooperative kinetics of aggregation, fibril formation, binding of the dye Congo red, and the cross-β x-ray diffraction pattern (12). The experimental evidence on GNNQQNY indicates that the amyloid-forming nucleus of a protein might consist of only a short segment of the entire chain. Furthermore, it has recently been shown that cytotoxicity is more pronounced for the early aggregates than for highly organized fibrillar structures (13). In this report, the free-energy surface of the very early steps of aggregation and the role of cross-strand side-chain interactions are investigated by implicit solvent (14) MD simulations of a trimer of the heptapeptide GNNQQNY. A set of mutant peptides are also simulated to explore the sensitivity to amino acid sequence.

Materials and Methods

Model.

The MD simulations and part of the analysis of the trajectories were performed with the charmm program (15). The peptide was modeled by the CHARMM PARAM19 force field, i.e., by explicitly considering all heavy atoms and the hydrogen atoms bound to nitrogen or oxygen atoms (15). An implicit model based on the solvent-accessible surface was used to describe the main effects of the aqueous solvent on the solute (14). The charmm param19 default cutoffs for long-range interactions were used, i.e., a shift function (15) was used with a cutoff at 7.5 Å for both the electrostatic and van der Waals terms. This cutoff length was chosen to be consistent with the parameterization of the force field and implicit solvation model. The model is not biased toward any particular secondary structure type. In fact, exactly the same force field and implicit solvent model have been used recently in MD simulations of folding of structured peptides (α-helices and β-sheets) ranging in size from 15 to 31 residues (16, 17, 18) and small proteins of about 60 residues (19, 20). Despite the lack of friction due to the absence of explicit water molecules, the implicit solvent model yields a separation of time scales consistent with experimental data: helices fold in ≈1 ns (21) [≈100 ns experimentally (22)], β-hairpins fold in ≈10 ns (21) [≈1 μs (22)], and triple-stranded β-sheets fold in ≈100 ns (23) [≈10 μs (24)].

Simulations.

All simulations were performed with three replicas starting from random conformations, positions, and orientations. In the initial random positions there was no intermolecular contact, i.e., the peptides were separated in space. The temperature was kept close to 330 K by weak coupling to an external bath with a coupling constant of 5 ps. A temperature of 330 K was chosen to get a statistically significant number of aggregation and disaggregation events in the time scale of the simulations. The MMFP option (25) of charmm was used to prevent the peptides from leaving a sphere of 150-Å diameter. The SHAKE algorithm (26) was used to fix the length of the covalent bonds involving hydrogen atoms, allowing an integration time step of 2 fs. The nonbonded interactions were updated every 10 dynamics steps and coordinate frames were saved every 20 ps for a total of 50,000 conformations per μs. A 1-μs run requires ≈20 days on a 1.4-GHz Athlon processor.

Progress Variables.

The conformations sampled at 330 K were used to define the aggregation contacts between in-register and out-of-register strands. Backbone and side-chain contacts were considered to be present if the C_α atoms were within 5.5 Å and the center of mass of the side chains was within 6.0 Å.

Normalized Frequency.

The normalized frequency of forming IP2 aggregates is given by

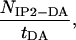1

where N_IP2-DA is the number of transitions between the disordered aggregates DA and the double stranded in-register aggregate IP2, and t_DA is the time during which the three peptides do not form ordered aggregates, i.e., Q_a ≤ 0.2 and Q_p ≤ 0.2.

Results and Discussion

Strategy to Simulate Aggregation.

Because the major goal of this report is to study the early steps of aggregation, MD simulations were performed with three peptide replicas. Although it is not known experimentally whether three peptides form a stable “nucleus,” the small number of replicas kept the complexity of the system and the CPU requirements low. Simulations were started from random conformations, positions, and orientations of the three replicas and carried out for 1 or 2 μs at 330 K (Table 1).

Table 1.

Simulations performed

Peptide sequence	No. of simulations	Length, μs	No. of IP3* aggregation events	No. of IA3† aggregation events
GNNQQNY	20	1	25 (14.9)‡	7 (3.1)
GNNQQNA	3	2	5 (2.9)	5 (3.1)
GNNQQNG	3	2	6 (3.6)	7 (2.8)
GNNQQN	2	2	2 (1.3)	3 (1.0)
GNNQQNNG	3	1	1 (6.5)	4 (11.0)
SQNGNQQRG	3	2	0	0
SENGNQQRG	3	1	0	0

Each trajectory simulates three replicas of a given sequence. 

^*Three-stranded parallel in-register aggregates. 

^† Three-stranded antiparallel in-register aggregates. 

^‡ The average time (ns) the replicas remained aggregated in IP3 and IA3 is given in parentheses. 

Aggregation Events.

In 20 simulations, the three replicas of the GNNQQNY heptapeptides formed 25 times an in-register parallel β-sheet (IP3), irrespective of the starting conformation of the peptides and their relative position and orientation (Fig. 1). The observed parallel packing of the β-strands is consistent with x-ray diffraction and Fourier transform infrared (FTIR) data (12). Yet, it is important to note that the experimental data supporting a parallel arrangement are not conclusive and in particular FTIR can be misleading on this point. Furthermore, the structure in the microcrystals is not necessarily the same as that in the amyloid fibrils. The average spacing between the β-strands in IP3 is 4.90 ± 0.12 Å (4.55 ± 0.14 Å after minimization). The in-register parallel β-sheet organization juxtaposes the polar residues asparagine and glutamine of neighboring peptide chains, as well as the aromatic rings of the tyrosines. This configuration enables the formation of, on average, 10 hydrogen bonds. The IP3 conformations sampled by MD are consistent with the suggestion of Balbirnie et al. (12) that a large number of side-chain hydrogen bonds contribute to the high density and stability observed for microcrystals of the GNNQQNY heptapeptides.

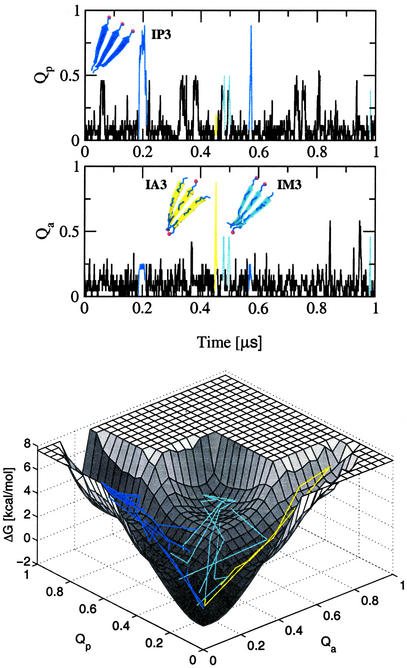
Figure 1.

(Upper) Time dependence of the fraction of in-register parallel contacts Q_p and in-register antiparallel contacts Q_a for one trajectory of the GNNQQNY peptide. Aggregation events to IP3, IM3, and IA3 are shown in blue, cyan, and yellow, respectively. (Lower) Projection of the aggregation events onto the free-energy surface (for the construction of the free-energy surface, see the text and the caption of Fig. 2).

The three replicas also formed seven times an in-register antiparallel (IA3) and 42 times an in-register mixed parallel–antiparallel (IM3) β-sheet during the 20 μs of simulation time (Fig. 1). These two types of in-register aggregates have a reduced kinetic stability compared with IP3. The latter is stable for an average of 14.9 ns, whereas IM3 and IA3 disaggregate, on average, after 8.0 and 3.1 ns, respectively. The antiparallel alignment of the strands forbids, partially in IM3 and completely in IA3, the interactions between the aromatic rings of the tyrosines. Moreover, the average number of side-chain hydrogen bonds is reduced to seven and five in IM3 and IA3, respectively. These findings are in agreement with theoretical results indicating that cross-strand interactions between side chains are required for the formation of stable β-sheets (27). The average distance between the antiparallel strands is 4.85 ± 0.15 Å (4.55 ± 0.38 Å after minimization), which is similar to the average observed for the parallel aggregate.

A total of 257 partial aggregation events to an in-register parallel (IP2) and 142 to an in-register antiparallel double-stranded β-sheet (IA2) occurred. The third strand did either not interact with the two-stranded aggregate or was forming out-of-register interactions with it. Hence, not only in-register but also out-of-register aggregates were observed in the simulations. A mixed β-sheet consisting of two parallel in-register strands and a third antiparallel one that is displaced by one residue (OM3) constitutes a special subgroup of IP2. OM3 is the only long-lived out-of-register aggregate. Thirty-nine aggregation events to OM3 were observed. With an average disaggregation time of 9.3 ns, its kinetic stability is even slightly higher than that of IM3. All other types of out-of-register aggregates with a displacement of more than one residue in any chain were short-lived and dissolved quickly. Moreover, a cluster analysis showed that IP3, IM3, and OM3 are the only highly populated three-stranded aggregates.

Several runs with control peptides (for a total of 28 μs) were performed to test the reliability of the simulation protocol (Table 1). Experimental studies on the nonapeptide, SQNGNQQRG (Sup35 residues 17–25 with the Gln/Arg mutation at position 24), showed solubility in vivo and in vitro and no formation of amyloid fibrils (12). Three 2-μs runs of SQNGNQQRG carried out with the same temperature and simulation protocols used for GNNQQNY did not show the formation of any stable in-register aggregates. Only three times did the SQNGNQQRG replicas aggregate into short-lived, parallel out-of-register β-sheets. These simulation results indicates that the force field and solvation model are not biased toward the formation of ordered aggregates. It is known that amino acid substitutions with charged residues can prevent fibril formation (28). The Arg at the C terminus might even prevent the early steps of in-register aggregation of SQNGNQQRG. On the other hand, Balbirnie et al. (12) have reported the in vitro formation of unbranched fibrils for the charged nonapeptide GNNQQNYQR. To investigate other possible reasons for the lack of ordered aggregates of SQNGNQQRG, an analysis of the out-of-register aggregates was performed. It was found that the φ-dihedrals of the central glycines fluctuate on average 74°, which is much more than the average of 22° for the other nonterminal residues. These torsional fluctuations lead to the disruption of backbone hydrogen bonds and, finally, disaggregation. The high torsional mobility of the central glycine might also contribute to the prevention of full in-register aggregation even when the N-terminal residues are correctly adjusted. To further investigate whether the lack of aggregation events in the SQNGNQQRG runs is a consequence of the central glycine or charge repulsion, three additional 1-μs simulations were performed with the mutant peptide SENGNQQRG. Although the replacement of the first Gln by a Glu in SENGNQQRG should favor the antiparallel β-sheet by the Glu–Arg side-chain interactions, no in-register aggregates were observed (Table 1). Hence, the simulation results indicate that the flexibility of Gly disfavors the formation of ordered aggregates.

Energy Surfaces.

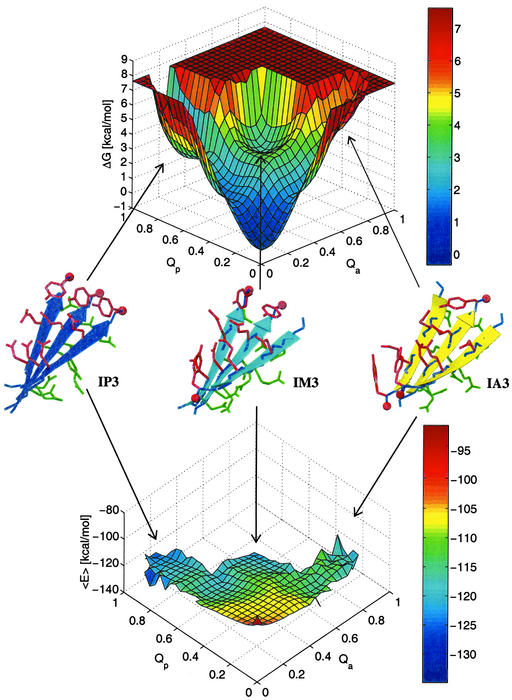
For a system in thermodynamic equilibrium, the difference in free energy in going from a state A to a state B is proportional to the natural logarithm of the quotient of the probability of finding the system in state A divided by the probability of state B. The sampling of several transitions between disordered and ordered aggregates indicates that the simulations are close to equilibrium. Moreover, the free-energy surfaces constructed from two independent sets of 10 simulations have the same shape and show a low average error (see caption of Fig. 2). The free-energy surface has three distinctive minima at IP3, IM3, and the disordered aggregates, which in this projection includes the soluble state, i.e., conformations with one or all isolated replicas (Fig. 2 Upper). IP3 (Q_p ≥ 0.75) is more stable than IM3 and has a free-energy difference of 2.8 kcal/mol from the disordered aggregates (Q_p ≤ 0.2 and Q_a ≤ 0.2), whereas the one between IM3 (Q_p ≥ 0.4 and Q_a ≥ 0.4) and the disordered aggregates is 3.3 kcal/mol. IP3 is also more stable than the out-of-register aggregate OM3, which collocates with IP2 (Q_p ≈ 0.5 and Q_a ≤ 0.2) on the energy surfaces. The free-energy difference of OM3 from the disordered aggregates was calculated from its population probability and is 3.1 kcal/mol.

Figure 2.

Free energy (ΔG, Upper) and average effective energy (〈E〉, Lower) surface at 330 K as a function of the fraction of in-register parallel, Q_p, and in-register antiparallel, Q_a, contacts. A total of 10⁶ conformations sampled during the 20 simulations at 330 K were used. 〈E〉 was evaluated by averaging the effective energy values of the conformations within a bin without minimizing them. ΔG was computed as −k_BT ln(N_n,m/N_0,0), where N_n,m denotes the number of conformations with n parallel and m antiparallel contacts. The error in ΔG is estimated by separating the 20 simulations into two sets of 10 simulations each. The average error of 〈E〉 is 1.2 kcal/mol, and the average error of ΔG is 0.2 kcal/mol. Representative conformations of IP3, IM3, and IA3 sampled along the MD trajectories are shown in blue, cyan, and yellow, respectively.

The average effective energy 〈E〉 (sum of intrapeptide, interpeptide, and solvation energy) as a function of the fraction of in-register parallel, Q_p, and in-register antiparallel contacts, Q_a, shows an overall downhill landscape (Fig. 2 Lower). The three minima on this surface correspond to IP3, IM3, and IA3, with a most pronounced minimum for IP3. The effective energy does not include the configurational entropy of the peptide, which consists of conformational and vibrational entropy contributions (29). Hence, the free-energy minimum of the disordered aggregates originates from an entropic advantage because the effective energy is very unfavorable. On the first view, the barriers between the disordered and ordered aggregates also seem to have only an entropical origin because the average effective energy appears rather smooth. However, a closer look reveals two barriers on the effective energy surface, one at Q_p = 0.7 and Q_a ≤ 0.2 and the other at Q_p ≤ 0.2 and Q_a = 0.7. The preceding regions (Q_p ≈ 0.5, Q_a ≤ 0.2 and Q_p ≤ 0.2, Q_a ≈ 0.5) correspond to IP2 and IA2, respectively. As described above, IP2 and IA2 appear either alone or with a third strand that is not in register. The latter conformations have a lower effective energy than the former because of the supplementary interactions with the chain out of register. However, these interactions have to be broken to reach an aggregate with all three strands perfectly aligned. Indeed, this was observed in 21 of the 25 aggregation events of IP3. In 19 of the 21, two strands first aggregated in register followed by the third one, which was displaced by two or more residues. After 0.7 ns, on average, the out-of-register strand detached and rearranged in register. In the two remaining cases, the out-of-register strand was displaced by only one residue, i.e., OM3 was formed before the in-register aggregation. Hence, an enthalpic barrier has to be crossed when an assembly with out-of-register contacts converts to a fully in-register aggregate. These results are in contrast to a purely downhill surface observed for 20-residue peptides that fold to a three-stranded antiparallel β-sheet (16, 17). The absence of a connection between the three peptide replicas results in a larger number of different low-energy states and an effective energy surface that is more rough than for a three-stranded β-sheet peptide.

Backbone and side-chain interactions contribute to the enthalpic barriers as seen in Fig. 3. However, the contribution of the backbone interactions is more pronounced, because most out-of-register strands mainly form backbone contacts. It is interesting to note that the backbone hydrogen bonds slightly favor the antiparallel arrangement (Fig. 3 Left), in agreement with previous energy-minimization studies (30). On the other hand, the interactions between side chains clearly favor the parallel aggregate by about −6.5 kcal/mol (Fig. 3 Right). Recently, it has been proposed that the π stacking between aromatic residues might contribute significantly to the thermodynamic stability of amyloid structures (31). In agreement with this suggestion, the most favorable energetic contribution to the stability of IP3 originates from the Tyr–Tyr interactions (Table 2). The interaction energies of the tyrosines are significantly lower than the minimal stacking energy of −6.6 kcal/mol, recently calculated for an optimal Tyr–Tyr alignment (32). However, in the calculation of the minimal stacking energy the tyrosines were modeled by p-cresol, whose ring centroids could adopt a distance of 3.7 Å in the optimal stacking configuration. In the simulations at 330 K, by contrast, the average distance between the ring centroids is 5.2 Å in IP3. Nonetheless, the stacking interactions between the aromatic rings of tyrosine, as well as the higher number of hydrogen bonds between the side chains of polar residues, result in a clear preference of the parallel over the antiparallel aggregation of GNNQQNY. This behavior seems strongly related to the asymmetry in the sequence. One may therefore wonder whether a palindromic sequence prefers to form antiparallel aggregates. To test this hypothesis, three 1-μs simulations were carried out for the palindromic sequence GNNQQNNG. The three replicas of this peptide aggregated four times in the antiparallel and only once in the parallel arrangement (Table 1). These results indicate that backbone hydrogen bonds seem to turn the balance in favor of an antiparallel in-register aggregate if side-chain interactions are equally favorable in IP3 and IA3, as is the case for palindromic sequences.

Figure 3.

Sum of van der Waals and electrostatic energies for the atoms in the backbone (Left) and in the side chains (Right) as a function of the fraction of in-register parallel, Q_p, and in-register antiparallel, Q_a, contacts. For clarity reasons, this plot has been rotated by 180° around a vertical axis with respect to Fig. 2.

Table 2.

Side-chain interaction energies in the IP3 conformation of GNNQQNY

Interacting pairs	Eelec*	EvdW†	Etot‡
Tyr–Tyr	0.0	−2.3	−2.3
Asn–Asn	−1.3	−0.8	−2.1
Gln–Gln	−0.5	−1.0	−1.5
Gln–Tyr	−0.5	−0.6	−1.1
Gln–Asn	−0.4	−0.5	−0.9

All energies are in kcal/mol. 

^*Electrostatic contribution to the interaction energy. 

^† van der Waals contribution to the interaction energy. 

^‡ Total interaction energy. 

Influence of Tyrosine on the Early Aggregation Events.

Alanine substitution experiments on short fragments of the islet amyloid polypeptide (IAPP) and amyloid β peptide (Aβ) showed that the aromatic residue Phe is crucial for their aggregation propensity (28, 33). It was proposed that interactions between aromatic residues might not only make a strong contribution to the thermodynamic stability of the amyloid structures but also provide order and directionality in the self-assembly. This hypothesis is investigated here by MD simulations of three mutants of the GNNQQNY peptide, which have no tyrosine (Table 1). If there is directionality in the self-assembly process, the peptides lacking the aromatic residue are expected to form in-register aggregates less frequently. The normalized frequencies to form IP2 (see Materials and Methods) are 18.5 ± 5.5 per μs for the wild-type peptide and 23.3 ± 8.9 per μs, 21.6 ± 4.4 per μs, and 15.9 ± 2.9 per μs for the GNNQQNA, GNNQQNG, and GNNQQN-mutant, respectively. The similarity in the frequencies to form IP2 aggregates indicates that the aromatic residue tyrosine does not provide more order to the aggregation process. On the contrary, GNNQQNA and GNNQQNG form IP2 aggregates slightly more often. However, the IP2 assemblies of the wild-type sequence are kinetically more stable than those of the mutants. The IP2 aggregate of the GNNQQNY peptide is stable for, on average, 3.2 ns, whereas the IP2 aggregate of the mutants disassociates already after 1.4 ns. The slower disaggregation of the wild-type peptide allowed that 9.7% of the 257 IP2 aggregates were elongated into IP3 by docking the third stand in register. This occurred for only 5.7% of the 226 IP2 aggregates formed in the mutant simulations.

Overall, the simulation results indicate that an aromatic residue does not give directionality to the self-assembly process but stabilizes the parallel aggregates. This increased stability gives the free strand more time to assemble in register. The aggregation process can formally be represented by the addition reaction (34)

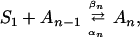2

where S₁ is an isolated peptide, A_n (n > 1) is the aggregate containing n peptides, and α_n and β_n are the disaggregation and aggregation rate constants, respectively. The critical nucleus of aggregation is reached when the aggregation and disaggregation rates are the same. In the simulations presented here, the initial aggregation rate constants, β₂, are similar for the peptides with and without an aromatic residue. By contrast, the disaggregation constants, α₂, are lower for the former. Although no predictions can be made for late rate constants (n > 3), the results suggest that, for a given monomer concentration, the peptides with a tyrosine reach the nucleus faster than the sequences lacking a tyrosine. Overall, the findings are consistent with the experimentally observed key role of aromatic residues in amyloid formation of peptides.

Conclusions

The present study shows that it is possible to simulate with an atomic model the early steps of aggregation of an amyloid-forming peptide. The simulations give insights into the energetics of the early assemblies and the strong sequence dependence of aggregation. Backbone hydrogen bonds favor the antiparallel β-sheet packing but side-chain hydrogen bonds and aromatic stacking stabilize the in-register parallel aggregate. Simulations with peptides lacking the tyrosine indicate that aromatic residues lower the disaggregation rate of parallel assemblies. The dependence of aggregation and disaggregation rates on the sequence might be an essential factor determining the time scale on which peptides reach the critical aggregation nucleus. Investigating other elements that influence nucleation is of major interest. Further studies of the dependence of aggregation kinetics on aromatic residues, charged residues (35), and peptide length by MD simulations might help to understand the nucleation of amyloidogenic peptides.

Abbreviation

MD

molecular dynamics