Abstract
We examine a hypothesized relationship between two descriptions of community structure: the niche-overlap dendrogram that describes the ecological similarities of species and the pattern of relative abundances. Specifically, we examine the way in which this relationship follows from the niche hierarchy model, whose fundamental assumption is a direct connection between abundances and underlying hierarchical community organization. We test three important, although correlated, predictions of the niche hierarchy model and show that they are upheld in a set of 11 communities (encompassing fishes, amphibians, lizards, and birds) where both abundances and dendrograms were reported. First, species that are highly nested in the dendrogram are on average less abundant than species from branches less subdivided. Second, and more significantly, more equitable community abundances are associated with more evenly branched dendrogram structures, whereas less equitable abundances are associated with less even dendrograms. This relationship shows that abundance patterns can give insight into less visible aspects of community organization. Third, one can recover the distribution of proportional abundances seen in assemblages containing two species by treating each branch point in the dendrogram as a two-species case. This reconstruction cannot be achieved if abundances and the dendrogram are unrelated and suggests a method for hierarchically decomposing systems. To our knowledge, this is the first test of a species abundance model based on nontrivial predictions as to the origins and causes of abundance patterns, and not simply on the goodness-of-fit of distributions.
A fundamental idea behind the study of patterns of species abundance is the presumed connection between species abundances and the functional ways in which communities are organized. Functional organization refers to how species are related to one another, as competitors or members of a web of interactions. The hypothesis that readily available data on relative abundances give insight into these less visible aspects of functional organization is not new (1, 2). For example, it is commonly observed that disturbed biotas are dominated by very few species and have a very different form of organization than their undisturbed and more diverse counterparts (3–5). Despite the importance of this fundamental connection for dialogues about conservation and biodiversity (6), and the century of effort that has gone into gathering data on species abundances, our understanding of these deeper aspects of community structure, and of how they connect to species abundances, remains poor.
Recent developments in models of species abundance have focused on the incorporation of species' dynamics (7) or on the use of spatially explicit individual-based models that include basic physiological processes (8). All of these models rely exclusively on the goodness-of-fit between theoretical and observed distributions for verification. A very interesting recent example is the approach by Hubbell (6), which is based on the basic processes of birth, death, migration, and speciation. It generates a class of flexible multinomial distributions whose various free parameters can be tuned to match some characteristics of recent data sets (i.e., lognormal distributions with a negative skew). Gross fits of theoretical distributions to data can be helpful as a first step in model validation; however, they are often not unique (especially when more free parameters are allowed), and nearly all are post hoc. A central aspect of Hubbell's neutral theory (and indeed of statistical ensemble arguments as a genre) is that all species are regarded as equivalent: all individuals of the community have the same probability of speciating, migrating, and dying. It is a beguilingly simple null hypothesis for the absence of biological uniqueness and structure. Although it can be tuned to fit the negatively skewed lognormal, it does not reproduce the ubiquitous canonical lognormal observed by Preston (9).
To our knowledge, the only species abundance model that actually “predicted” negatively skewed lognormal abundance distributions and reproduced the canonical lognormal was the niche hierarchy model (10, 11). This model requires individual species variation by asserting that species abundances are connected to the unique functional ways in which communities are organized (1–4, 12, 13). This structure can be summarized by dendrograms of niche overlap. A community that is organized along a gradient of increasing niche similarity can be sequentially broken down into a nested hierarchy of smaller and more tightly related species groups. Aside from heuristic convenience, there is evidence from the formal topological structure of food webs that tree-like dendrograms are natural descriptions of many communities (14, 15).
The niche hierarchy model (11) posits a direct correspondence between this particular conception of community structure and species abundance. A physical metaphor for transforming dendrograms into abundances is sequential breakage. We explore this connection and report new evidence that demonstrates the empirical correspondence between species abundance patterns and the structure of niche-overlap dendrograms (11, 14). Our findings have special relevance to the neutral hypothesis, because they cannot be accounted for by existing statistical models disregarding variation in species traits. Moreover, they are based on nontrivial model predictions and not simply on the goodness-of-fit of observed versus theoretical abundance distributions.
The Niche Hierarchy Model
One of the most familiar models or metaphors aimed at shedding light on observed patterns of species abundances is MacArthur's “broken stick” (1). He imagined a homogeneous resource axis (“the stick”) simultaneously broken at random into several pieces. Each species' abundance is reckoned to be directly proportional to the size of its piece. This depiction of apportionment with respect to a single resource axis is the defining assumption in essentially all so-called resource apportionment models (13, 16, 17).
By contrast, such homogeneity is not required in the niche hierarchy model, where the breakages are sequential (11). To illustrate, one can imagine a community of birds where the first split at the base of the dendrogram divides the community into those birds that forage primarily on the ground versus those that forage in trees. Of those that forage in trees, this group can be further split into those that forage along the trunk versus those that forage in branches. The trunk feeders may be further split into those that eat one type of surface grub versus those that eat another subbark grub, and so on. The branch dwellers may in turn be divided by yet other ecologically important differences until the dendrogram is eventually resolved to the level of individual species. Accordingly, a species' abundance can be thought of as a product of multiplicative factors (niche interfaces) that nest hierarchically and sequentially to constrain the final abundance. The splits in the dendrogram are thought of as describing different niche interfaces (11). The sequence of interfaces generates a sequence of multipliers that determine relative abundances.
This is a “niche-ordering model” rather than simply a model of resource apportionment. The mechanism of sequential breakage is simply a physical metaphor for mapping from the underlying dendrogram to abundances. It is a quantitative guide that yields testable predictions about abundances and their relationship to the dendrogram. The ordering is the sequence of multipliers corresponding to branch points in the dendrogram whose product describes the nested constraints that determine abundances. This multiplicative “niche-ordering rule” has been referred to as the “splitting or breakage sequence” (11).
A dendrogram provides a “partial ordering” of species insofar as the resource base is heterogeneous (14). The more homogenous and low dimensional the resource base, the more unevenly branched the dendrogram, leading ultimately to a perfect ordering (Fig. 1b). For example, if only one factor is at work in structuring the community, then one can always produce a perfect ordering of species: no two species are exactly alike, and they can be ranked in perfect order with regard to the factor. By contrast, a partial ordering describes a case where distant parts of a dendrogram belonging to different branches may describe a splitting sequence that involves different constraining factors (e.g., different resources or niche interfaces) and thus are not directly comparable. When species cannot be ordered along one axis with respect to each other, we have a partial ordering. This metaphorical splitting process, or niche-ordering model, expresses the idea that communities do indeed ultimately assemble themselves by such processes. Or, to put it another way, insofar as communities can be said to evolve (remembering always that Darwinian evolution acts on individuals, not populations, much less communities), this “niche splitting” process is a plausible one. By the same token, environmental disturbance or changes in interactions among populations (resulting, for instance, from invasions) can, over time, change both dendrograms and abundances, although in correlated ways.
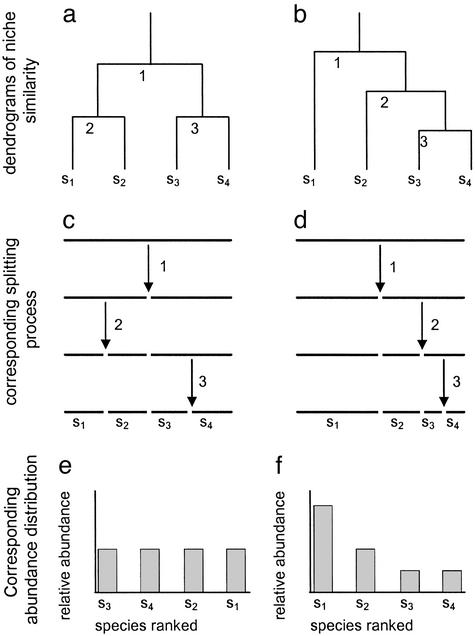
Figure 1.
Two dendrograms depicting the organization of a hypothetical four species (s1 to s4) community. (a) A symmetrical branching structure; (b) an asymmetric one. The sequential splitting process (a physical metaphor for the nested ordering of niche interfaces) is shown in c and d for the dendrograms a and b, respectively. Numbers correspond to the bifurcations in the dendrograms, with 1 being the root (lowest similarity). The corresponding abundance distributions are given in e and f. Note that the abundances in f that follow from an asymmetrical branching structure b are less equitable than in e, where the underlying dendrogram a was more evenly branched.
Two decisions need be made for this model to generate relative abundances. The first decision concerns the so-called binary apportionment rule. This is essentially the probability density function of fractional splits (multipliers) for the two-species case. It is the rule that determines how binary breakages are made at each step: uniformly randomly or otherwise. Because each breakage will produce two fractions of size x and 1 − x, this distribution is symmetric on (0, 1). Consequently, the interval (0.5, 1) is sufficient to describe it (11). This rule was determined empirically from known two-species cases, and the distribution for the more abundant member of the pair was found to be roughly triangular on the interval 0.5 to 1 with a mode between 0.6 and 0.8. Thus on average, the dominant species is roughly three times as abundant as the other member of the pair (see figures 4 and 5 in ref. 11).
The second decision concerns the niche-ordering rule or breakage sequence. This is where the connection to the dendrogram begins. The splitting sequence determines which fragment will be chosen to be further split. For example, in Tokeshi's (13) dominance decay model, the largest fragment is always chosen to be further split. In contrast, the ordering rule of the niche hierarchy model is set by the dendrogram, without reference to the size of the fragments. Each branch point in the dendrogram defines a separate split between two species or two groups of species (Fig. 1). Each species' abundance is determined by a sequence of multiplicative split factors (x or 1 − x, where 0 < x < 1 comes from the binary apportionment rule) tracing from the root to the terminal branch.
In the original exposition (11), a fixed ratio of 0.75, was adopted for the apportionment rule, and the splitting sequence was random with successive fragments to be split chosen independently of its size. This earlier deterministic rule was used as a surrogate (the spatial average) for the triangular distribution, the latter being the depiction of a random binary tree, which is the “minimal” assumption when the shape of the dendrogram of niche overlap is unknown. This was the case for the data sets examined at that time (11). It is interesting to observe that the application of the above two decisions or rules yields distributions of species abundance that closely resemble the canonical lognormal distribution of Preston (9). The model thus provides a minimal biological explanation (with no post hoc fitting) for a distribution known successfully to describe many empirical abundance data (13), including an explanation for why the species area exponent has a value of z ≈ 1/4 (S ≈ cAz) (18). Nearly a decade later, it was found that for large data sets, the model generates lognormal distributions with a characteristic negative skewness, thereby allowing Nee, Harvey, and May (10) to accurately predict the excess of rare species that they observed in the British bird census data. This earlier work is not discussed by Hubbell (6), who suggests the neutral theory is the only one that generates such skewed distributions.
Although the niche hierarchy model can reproduce several features seen in nature, these tests are based on goodness-of-fit between observed and theoretical distributions. Goodness-of-fit tests are certainly a valuable initial approach to test a model (19), but they are far from definitive. Almost always, many alternative models can be produced that yield similar fits. Such tests alone cannot provide any guarantee that the model is correct, or even interesting, and this problem is not new in the field of species abundance models (20). An additional step in the validation of a model is to test its assumptions and further implications (if there are any). This is possible here, because the model generates several nontrivial predictions concerning the link between species abundances in a community and the operating dendrogram of niche similarity. We now suggest several ways to test it that we think provide new insight into species abundance patterns.
Methods and Results
Data Sets.
The sole criterion in selecting studies to include in the tests was that they contain both a dendrogram and an abundance list. These are hard to find together. We found 11 such studies from the literature, involving fishes, amphibians, lizards, and bird communities (Table 1). Note that these studies are essentially limited to communities that are taxonomically homogeneous. We believe a degree of homogeneity is required insofar as the members of these communities must be linked by some sequential or nested chain of commonality. We do not expect to find any obvious relationship when the assemblage is excessively heterogeneous, so that there is no fundamental common root, i.e., when the underlying resource (niche) space is unconnected (11). In the data sets, abundances are measured by population biomasses, that is, by density or total abundance times body weight, except for the lizards and amphibians, for which information on body mass was lacking. For simplicity, we shall call these “abundances.” Whether to use abundance, biomass, or energy is potentially problematic (21). It is, however, not a sensitive issue here, because the relationship between body weight and energy consumption is only mildly nonlinear (22), and because it has been found that energy and abundance partitioning appear to be nearly equivalent processes (21, 23–26). Finally, we note that in no case did the construction of the dendrograms ever involve the use of abundances as a discrimination criterion, in which case the hypothesized relationship would be tautological. Yet there are likely to be relationships between body size and some factors used to construct the dendrogram and between body size and population abundance (27, 28). Nonetheless, we see no general way in which such a degree of interdependence between the dendrogram and abundance could spuriously generate our observations.
Table 1.
Catalogue of the 11 data sets that provide both species abundances and a dendrogram of niche similarity
| Fig. 3 graph | Taxonomic group and study site | Ecological descriptors | Similarity or distance index | Clustering method | Ref. |
|---|---|---|---|---|---|
| a | Fishes, Rio Manso, Brazil | Ecomorphology (15) | Pearson r | Ward | 42 |
| b | Amphibians, tropical forests, Mt. Kupe, Cameroon | Morphology (2) and microhabitat use (28) | Gower similarity | UPGMA | 43, 44 |
| c | Lizards, tropical forests, Mt. Kupe, Cameroon | Morphology (1) and microhabitat use (18) | Gower similarity | UPGMA | 43, 44 |
| d–g | Birds, four types of Ponderosa pine forest, U.S. | Activity, foraging methods and sites (7) | Euclidean distance | UPGMA | 45 |
| h | Birds, Hubbard Brook forest, U.S. | Foraging methods (27) | Euclidean distance | Complete link | 46, 47 |
| i | Birds, mixed forest, Australia | Foraging methods (25) | Euclidean distance | Complete link | 48 |
| j | Warblers, Himalayan slopes, Pakistan | Morphology (6) and foraging methods (4) | Gower similarity | UPGMA | 44, 49 |
| k | Waterfowl, Finland | Feeding methods (17) | Percentage similarity | UPGMA | 50 |
Numbers in parentheses indicate the number of descriptors retained in the studies. Letters a to k refer to the graphs in Fig. 3.
(i) Test of the Niche-Ordering Rule (Sequential Niche Fragmentation).
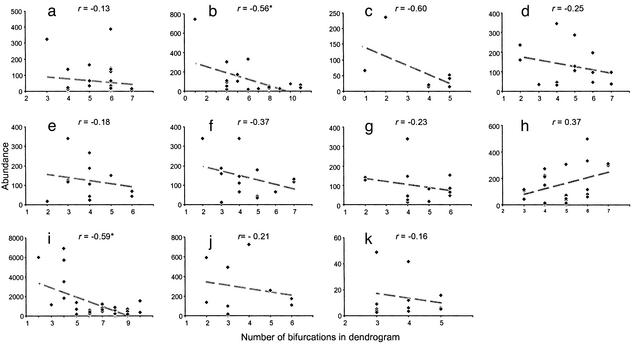
According to the niche hierarchy model, a species whose niche is highly nested in a dendrogram will have a corresponding “niche fragment” that has been subdivided many times. This niche fragment should be smaller on average than one that has fewer subdivisions. Thus we should expect, on average and with individual exceptions, to find an inverse relationship between the abundance of a species and its position in a dendrogram (as measured by the number of bifurcations to this species; see Fig. 2). This relationship would be unambiguous if the fractions were always halved, but given the probabilistic divisions, it can occasionally happen that fractions divided many times are sometimes the largest. In short, we should not expect an inverse relationship to hold in all cases, nor should we expect a statistically significant relationship in communities with very few species. A workable way to test the presumed link between abundances and dendrograms is to gather data from a variety of different communities and perform a simple metaanalysis as follows. Compute the Pearson correlation between abundances and the number of bifurcations for each community in the ensemble. Then compute the binomial probability of obtaining the observed number of negative correlations, under the null hypothesis that negative and positive values are equally likely. Although few of the individual correlations are significant (Fig. 3), as expected, we find a predominance of negative relationships between abundance and number of bifurcations in the niche overlap dendrogram. Only one correlation is positive, which yields a significant binomial probability of 0.012 for the ensemble.
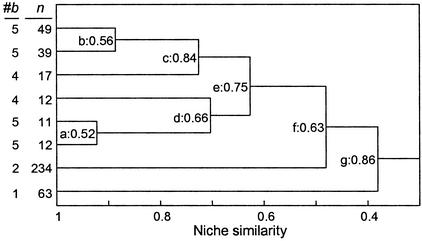
Figure 2.
Dendrogram of niche similarity for the lizards inhabiting the tropical forests of Mt. Kupe, Cameroon. n, abundance; #b, number of bifurcations from the root to a terminal node. (a–g) Bifurcations and the corresponding fractional abundance; for bifurcation c, fractional abundance = max (49 + 39,17)/(49 + 39 + 17). See Fig. 3c for the relationship between n and #b. (Top to bottom) Species are C. montium, Chameleo pfefferi, Leptosiaphos sp.A, Cnemaspis koehleri, L. sp.B, L. sp.C, R. spectrum, and Chameleo quadricornis.
Figure 3.
Relationship between species abundance and the number of bifurcations in the dendrogram of niche overlap. See Table 1 for summary. Pearson's correlations are given; * denotes an individual P value significant at the 0.01 level. All correlations are negative except for h. The binomial null hypothesis for the ensemble is rejected with a probability of 0.012. There is a significant negative correlation between a species' abundance and how highly nested it is in the dendrogram, suggesting that species with many niche interfaces are generally less abundant than those with fewer.
(ii) Test of Evenness–Shape Correlation.
Here we test the predicted positive correspondence between equitability in abundances and symmetry in the shape of the dendrogram. We measure evenness in abundances by the probability of interspecific encounter (29), an unbiased estimator. The symmetry of the dendrogram was measured by the shape statistic ρ derived by Siegel and Sugihara (30):
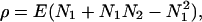 |
with N1 the number of edges (branches) from terminal node ν1 to the nearest common ancestor of terminal nodes ν1 and ν2 (e.g., in Fig. 2, for ν1 = Chameleo montium and ν2 = Rampholeon spectrum, N1 = 4 and N2 = 1). This index was then normalized by the range between the minimum and maximum value of ρ for the given number of species; this standardized index (ρst) equals 0 for perfect ordering as in Fig. 1b and 1 for the most symmetric dendrogram as in Fig. 1a.
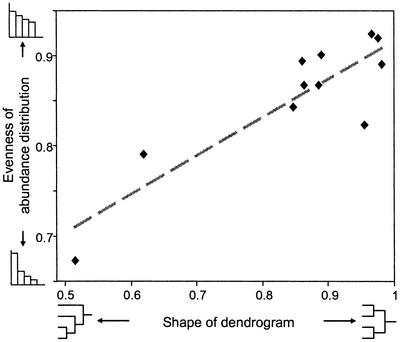
Fig. 4 presents the relationship between the shape of the dendrogram and the evenness of the abundance distribution. As predicted, communities with asymmetrical dendrograms have abundance distributions more uneven than those exhibiting symmetrical structure. The observed relationship between the shape of the dendrogram (ρst) and evenness (probability of interspecific encounter) yields a correlation coefficient r = 0.88, with P < 0.001. This relationship remains significant after controlling for the effect of species richness (S) on evenness (partial r = 0.82, P = 0.004). In sum, predictions of the niche hierarchy model due to niche ordering (sequential niche fragmentation) are upheld. Abundances can give insight into less visible aspects of community organization.
Figure 4.
Relationship between the shape of the dendrogram and the evenness of the abundance distribution for the 11 studies of Table 1. As predicted by the niche hierarchy model, asymmetric dendrograms have lower evenness than symmetric ones (Pearson correlation r = 0.88, P < 0.001). Thus abundances can give insight into less visible aspects of community organization.
(iii) Recovering the Binary Apportionment Rule.
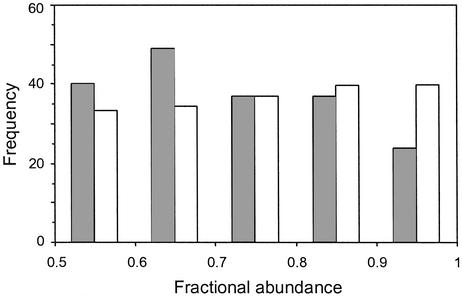
Sugihara (11) looked at assemblages containing two closely related species. These data revealed a triangular frequency distribution that was consistent with random breakages involving multiple factors where the dominant species gets the larger share of each factor. As noted earlier (11), the latter assumption is not likely to be valid for assemblages containing many species: there will be breakages where the species that gets the larger fraction on some dimensions will get the smaller fraction on other dimensions. The resulting binary apportionment distribution will be expected to have a mode shifted to the left (e.g., right-skewed triangular). If indeed there is a correspondence between the dendrogram and associated abundances, one should be able to recover this binary breakage rule by working backwards from the dendrogram as follows. Treat each bifurcation point of a dendrogram as an aggregated two-species case. For each branch point, add up the abundances of all species in each limb and compute the fractional abundance of the greater limb (see Fig. 2 for a worked example). The frequency distribution of these fractions regenerates the binary apportionment rule. The distribution of fractional abundances for the 11 studies pooled is shown in Fig. 5. As expected, it is right-skewed triangular with a mode in the interval 0.6–0.7. Similar-shaped distributions with a mode in the interval 0.6–0.7 are obtained for terminal and deeper branches; however, the significance of this distribution for deep branches is questionable, because sample size decreases as a power of 2 with each deeper split. It seems plausible that these deeper splits may have a more uniform or random distribution.
Figure 5.
Binary apportionment rule: frequency distribution of pair-wise fractional abundances of all bifurcations of the 11 data sets. Shaded bars, observed distributions; open bars, null distribution obtained by randomly shuffling the observed abundances in the observed dendrograms. Observed distributions differ significantly from their randomized counterpart (P = 0.005).
To determine the statistical significance of this result, we use a conservative permutation test, where the known set of abundances is randomly shuffled in the known dendrogram. For each permutation, we compute the binary apportionment rule (see Fig. 5), which is repeated for 2,000 permutations to yield the expected null distribution for a given community. Because the number of species in an examined community is often too small to allow for a meaningful computation of χ2, we pool the fractional abundances of all communities to generate the ensemble observed frequency distribution. The permuted distribution was similarly obtained by pooling the simulations for all communities. This exercise shows that the derived breakage distribution in Fig. 5 differs significantly from distributions obtained by reshuffling the abundances in the known dendrograms (randomization test, P = 0.005).
Interestingly, the binary apportionment rule derived here (Fig. 5) is right-skewed triangular with a mode close to 0.66, whereas a mode at 0.75 was found for replicate two-species assemblages (11). As noted by Siegel and Sugihara (30), a triangular distribution with a mode at 0.75 does not generate canonical lognormal distributions as closely as does a skewed-triangular distribution with a mode at 0.66 [in fact, there is a broad family of distributions that will generate canonicity (30)]. This discussion is interesting but somewhat peripheral in the present context. What is important to keep in mind concerning our empirically deduced apportionment rule is that it cannot be generated by randomly shuffling the observed abundances in the dendrogram. Moreover, the shape of this distribution may shed light on hidden aspects of resource sharing (see figure 5 in ref. 11).
Discussion
Our study demonstrates a link between two classical notions of community organization: species abundance and dendrograms of niche similarity. By linking community organization and dendrograms of niche similarity, the niche hierarchy model provides a framework for understanding the effects of ecological factors on abundance distributions.
In this vein, one may ask what the extremes in dendrogram branching patterns (symmetrical versus asymmetrical) may represent? One can expect to find an asymmetric branching pattern where a single ecological factor dominates and a more even branching pattern where multiple factors are important (14). For example, if colonization precedence is the single dominating variable structuring a community, then it is possible to generate a perfect ordering among the species corresponding to who gets there first. On the other hand, if other independent ecological factors come into play, then it may no longer be possible to generate a perfect ordering for the community. The result would be a more evenly branched portrait of niche relationships. The model thus predicts that the abundance distributions of communities influenced by a single strong and dominating ecological factor will be disequitable (similar to the geometric series), whereas those governed by multiple unrelated factors will have more equitable distributions (like the lognormal or the broken stick). This prediction is clearly amenable to experimental tests (31). Ruth Patrick's nutrient enrichment studies involving diatoms (2) and the Rothamstead Parkgrass experiments are among the best-documented examples of a decrease in evenness in species abundance distribution after a perturbation (32, 33). However, it is unknown in either case whether dendrograms of niche similarity became more asymmetric with this shift toward uneven abundances. This is fertile ground for future study.
We believe that the generality and interest of these findings is reinforced by the diversity of communities where they are found; however, as always, more data would be welcome. In this regard, we see the standardization of methods as being an important consideration for future work. Finding the correct niche overlap dendrogram is important for practical and methodological reasons. It is well known that different clustering methods can yield dendrograms of different shapes (34). In this regard, we advocate the use of “intermediate” methods such as Ward's minimal variance, UnweightedPair Group Method with Arithmetic Mean (UPGMA), or intermediate linkage as being preferable to those distorting the Euclidean space, such as the complete linkage or the single linkage method. A more difficult aspect is the choice of adequate ecological descriptors of the species to compute niche overlap (35). One wants the relevant dendrogram operating at a given time. Although it is customary to regard communities as being organized around trophic resources, there is nothing in the niche hierarchy argument that excludes any other factor. Thus, “enemy free space” may be an important factor structuring the community (36). The factors may be transient, with a different dendrogram early in succession than later. It is this abstract space that the model assumes is sequentially partitioned. Space itself is often used as a surrogate for limiting resources (6). In this vein, habitat itself could be split (37), and microhabitat use is a widespread descriptor of the niche (38, 39). In sum, the choice of an adequate set of descriptors is not trivial and may affect the perceived organization of the community. In an ideal world, all of these problems call for standardization in future metaanalysis.
Finally, it is worth noting that this model has empirical connections with topological regularities found in food webs, namely the excess of interval food webs (40), the prevalence of rigid circuits in niche overlap graphs (38), and the topological unholiness of simplicial niche space (14). These regularities support the formal mathematical result that underlying tree structures (hierarchies) follow naturally from the overlying topology (14). Moreover, they give rise to a simple necessary and sufficient assembly rule: new species entering the community tend to compete predominantly within single guilds (15, 41). As an example, with a bird community composed of two feeding guilds, one of seed eaters and one of insectivores, a newcomer would in general be less likely to enter if it consumes both kinds of food. This simple rule generates hierarchical structures that can be captured by dendrograms of niche similarity, which in turn provide the recipes for sequentially decomposing communities into simpler parts.
We note that this model is not limited to producing canonical lognormal distributions (11). It can produce a wide range of distributions depending on the underlying organization of the community. In Hubbell's terminology, the niche-ordering paradigm places this model in the “niche-assembly” camp (6). By contrast, Hubbell's neutral theory (6) takes the “dispersal-assembly” perspective. Although the mechanisms in niche ordering and dispersal may appear different and are potentially operating on very different time scales, the models are not mutually exclusive. It is possible that the most constructive view is to see real communities as being constrained by both niche-ordering and dispersal-assembly dynamics, with each providing a model that caricatures the governing forces. Nonetheless, the power of any model is measured by the insight it provides and the richness of the predictions it makes (with minimal parameter tuning), and these predictions should be verifiable.
Acknowledgments
We thank A. Davison, P. Harvey, C. Hsieh, J. Lawton, S. Levin, B. Maurer, and anonymous referees for help and comments. This research was supported by grants from the Office of Naval Research and a Fellowship from Merton College (to G.S.), the Swiss National Science Foundation, and partly by the Novartis Foundation and National Center of Competence in Research Plant Survival (to L.-F.B.), and the Leverhulme Trust (to R.M.M.).
Abbreviation
- UPGMA
Unweighted Pair Group Method with Arithmetic Mean
References
- 1.MacArthur R H. Proc Natl Acad Sci USA. 1957;43:293–295. doi: 10.1073/pnas.43.3.293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Patrick R. Am Nat. 1968;102:173–183. [Google Scholar]
- 3.Tilman D. Monogr Popul Biol. 1982;17:1–296. [PubMed] [Google Scholar]
- 4.Wilson S D, Tilman D. Oecologia. 1991;88:61–71. doi: 10.1007/BF00328404. [DOI] [PubMed] [Google Scholar]
- 5.May R M. In: Ecology and Evolution of Communities. Cody M L, Diamond J M, editors. Cambridge, MA: Belknap/Harvard Univ. Press; 1975. pp. 81–120. [Google Scholar]
- 6.Hubbell S P. The Unified Neutral Theory of Biodiversity and Biogeography. Princeton, Oxford: Princeton Univ. Press; 2001. [Google Scholar]
- 7.Diserud O H, Engen S. Am Nat. 2000;155:497–511. doi: 10.1086/303339. [DOI] [PubMed] [Google Scholar]
- 8.Pachepsky E, Crawford J W, Brown J L, Squire G. Nature. 2001;410:923–926. doi: 10.1038/35073563. [DOI] [PubMed] [Google Scholar]
- 9.Preston F W. Ecology. 1962;43:185–215. [Google Scholar]
- 10.Nee S, Harvey P H, May R M. Proc R Soc Lond Ser B. 1991;243:161–163. [Google Scholar]
- 11.Sugihara G. Am Nat. 1980;116:770–787. doi: 10.1086/283669. [DOI] [PubMed] [Google Scholar]
- 12.Fisher R A, Corbet A S, Williams C B. J Anim Ecol. 1943;12:42–59. [Google Scholar]
- 13.Tokeshi M. Adv Ecol Res. 1993;24:111–186. [Google Scholar]
- 14.Sugihara G. Ph.D. thesis. Princeton, NJ: Princeton Univ.; 1982. [Google Scholar]
- 15.Sugihara G. In: Population Biology. Proceedings of Symposia in Applied Mathematics. Levin S A, editor. Vol. 30. Providence, RI: Am. Math. Soc.; 1984. pp. 83–101. [Google Scholar]
- 16.Motomura I. Zool Mag (Tokyo) 1932;44:379–383. [Google Scholar]
- 17.Southwood T R E. Philos Trans R Soc London Ser B. 1996;351:1113–1129. [Google Scholar]
- 18.Sugihara G. Am Nat. 1981;117:790–793. [Google Scholar]
- 19.Bersier L F, Sugihara G. J Anim Ecol. 1997;66:769–774. [Google Scholar]
- 20.Cohen J E. Am Nat. 1968;102:165–172. [Google Scholar]
- 21.Harvey P H, Godfray H C J. Am Nat. 1987;129:318–320. [Google Scholar]
- 22.Brown J H, Marquet P A, Taper M L. Am Nat. 1993;142:573–584. doi: 10.1086/285558. [DOI] [PubMed] [Google Scholar]
- 23.Sugihara G. Am Nat. 1989;133:458–463. [Google Scholar]
- 24.Pagel M D, Harvey P H, Godfray H C J. Am Nat. 1991;138:836–850. [Google Scholar]
- 25.Taper M L, Marquet P A. Am Nat. 1996;147:1072–1086. [Google Scholar]
- 26.Cyr H. In: Scaling in Biology. Brown J H, West G B, editors. Oxford, U.K.: Oxford Univ. Press; 2000. pp. 267–295. [Google Scholar]
- 27.Nee S, Read A F, Greenwood J J D, Harvey P H. Nature. 1991;351:312–313. [Google Scholar]
- 28.Blackburn T M, Gates S, Lawton J H, Greenwood J J D. Philos Trans R Soc London Ser B. 1994;343:135–144. [Google Scholar]
- 29.Hurlbert S H. Ecology. 1971;52:577–586. doi: 10.2307/1934145. [DOI] [PubMed] [Google Scholar]
- 30.Siegel A S, Sugihara G. J Appl Probab. 1983;20:158–164. [Google Scholar]
- 31.Cowie P R, Widdicombe S, Austen M C. Mar Biol. 2000;136:485–495. [Google Scholar]
- 32.Kempton R A. Biometrics. 1979;35:307–321. [Google Scholar]
- 33.May R M. In: Theoretical Ecology; Principles and Applications. May R M, editor. Sunderland, MA: Sinauer Associates; 1981. pp. 197–227. [Google Scholar]
- 34.Legendre L, Legendre P. Numerical Ecology. Amsterdam: Elsevier; 1983. [Google Scholar]
- 35.Colwell R K, Futuyma D J. Ecology. 1971;52:567–576. doi: 10.2307/1934144. [DOI] [PubMed] [Google Scholar]
- 36.Jeffries M J, Lawton J H. Biol J Linn Soc. 1984;23:269–286. [Google Scholar]
- 37.Kolasa J. Ecology. 1989;70:36–47. [Google Scholar]
- 38.Inger R F, Colwell R K. Ecol Monogr. 1977;47:229–253. [Google Scholar]
- 39.Jones M, Mandelik Y, Dayan T. Ecology. 2001;82:2164–2176. [Google Scholar]
- 40.Cohen J E. Food Webs and Niche Space. Princeton, NJ: Princeton Univ. Press; 1978. [Google Scholar]
- 41.Sugihara G. In: Proceedings of an International Symposium Held in Kyoto, November 10–15, 1985. Teramoto E, Yamaguchi M, editors. Berlin: Springer; 1987. pp. 53–59. [Google Scholar]
- 42.Beaumord A C. Master's thesis. Rio de Janeiro, Brazil: Universidade Federal; 1991. [Google Scholar]
- 43.Hofer U, Bersier L F, Borcard D. Ecology. 1999;80:976–988. [Google Scholar]
- 44.Hofer U. Ph.D. thesis. Neuchâtel, Switzerland: Université de Neuchâtel; 2000. [Google Scholar]
- 45.Szaro R C, Balda R P. Studies in Avian Biology. Vol. 3. Allen, Lawrence, KS: Cooper Ornithological Society; 1979. Bird Community Dynamics in a Ponderosa Pine Forest. [Google Scholar]
- 46.Holmes R T, Bonney R E, Pacala S W. Ecology. 1979;60:512–520. [Google Scholar]
- 47.Holmes R T, Sherry T W, Sturges F W. Ecol Monogr. 1986;56:201–220. [Google Scholar]
- 48.Holmes R T, Recher H F. Condor. 1986;88:427–439. [Google Scholar]
- 49.Price T. J Anim Ecol. 1991;60:643–664. [Google Scholar]
- 50.Poysa H. Oikos. 1983;40:295–307. [Google Scholar]