A sensitive, versatile microfluidic assay for bacterial chemotaxis

Abstract

We have developed a microfluidic assay for bacterial chemotaxis in which a gradient of chemoeffectors is established inside a microchannel via diffusion between parallel streams of liquid in laminar flow. The random motility and chemotactic responses to l-aspartate, l-serine, l-leucine, and Ni²⁺ of WT and chemotactic-mutant strains of Escherichia coli were measured. Migration of the cells was quantified by counting the cells accumulating in each of 22 outlet ports. The sensitivity of the assay is attested to by the significant response of WT cells to 3.2 nM l-aspartate, a concentration three orders of magnitude lower than the detection limit in the standard capillary assay. The response to repellents was as robust and easily recorded as the attractant response. A surprising discovery was that l-leucine is sensed by Tar as an attractant at low concentrations and by Tsr as a repellent at higher concentrations. This assay offers superior performance and convenience relative to the existing assays to measure bacterial tactic responses, and it is flexible enough to be used in a wide range of different applications.

Bacteria swim by rotating semirigid helical filaments using bidirectional, ion-driven rotary motors. In Escherichia coli, the left-handed helical flagellar filaments form a bundle when the motors turn counterclockwise (viewed down the filament toward the cell), and the cell swims in a gently curved path known as a run. When a flagellar motor switches to clockwise rotation, the bundle is disrupted, and the cell undergoes a rapid change in swimming direction known as a tumble. An E. coli cell thus performs a 3D random walk in which runs of a few seconds alternate with tumbles on the order of a tenth of a second.

When a cell moves toward higher concentrations of attractant or lower concentrations of repellent, clockwise flagellar rotation and, hence, tumbling are suppressed. The random walk is thereby biased so that the cell migrates up an attractant gradient or down a repellent gradient. Gradients are sensed as temporal changes in concentration by comparing the instantaneous concentration with the concentration the cell experienced a few seconds earlier. Ligands are sensed by one of five membrane-spanning receptors, and temporal comparisons involve an adaptation process in which occupied receptors are covalently methylated, on a time scale of seconds, to reset their sensitivity and signaling capacity. The receptors are: Tar (taxis toward aspartate and away from certain repellents), Tsr (taxis toward serine and away from certain repellents), Tap (taxis toward di- and tripeptides), Trg (taxis toward ribose and galactose), and Aer (aerotaxis). Motility and chemotaxis are reviewed in refs. 1 and 2, respectively.

Modern studies on bacterial chemotaxis began in the 1960s with the work of Julius Adler (3, 4), which showed that bacteria use specific receptors to recognize chemicals. Intensive research since then has made chemotaxis in E. coli the behavior best understood at the molecular level. Four methods are commonly used to analyze the behavior: swarm plates, capillary assays, temporal stimulation of tethered cells, and automated tracking of swimming cells. Each method leaves something to be desired. An assay is needed that provides equally high sensitivity to attractants and repellents and that can be run in minutes. Here, we describe a sensitive, versatile, convenient, and biologically relevant assay that exploits microfluidic technology (5, 6).

Materials and Methods

Strains and Plasmids.

The strains and plasmids used in this study are listed in Table 1.

Table 1.

Strains and plasmids

	Genotype	Reference
Strains
RP437	thr(Am)1, leuB6, his-4, metF(Am)159, eda-50, rpsL1356, thi-1, ara-14, mtl-1, xyl-5, tonA31, tsx-78, lacY1, F−	7
MM509	RP437 eda+ Δ(tar-tap)5201	8
SW10	RP437 thr+ Δtsr7021	This study
VB13	RP437 eda+ thr+ Δtsr7021 Δ(tar-tap)5201 trg∷Tn10	9
MM5000	Rp437 eda+ ΔmotAB	10
RP3098	RP437 Δ(flhA-flhD)	11
Plasmids
pBAD18	araC paraBAD bla (Ampr)	12
pBJC100	pBAD18 with gfp cloned behind paraBAD	13

Materials.

Ampicillin, EDTA, l-aspartic acid, l-serine, l-leucine, l-arabinose, l-methionine, NiSO₄, and sodium d-lactate were purchased from Aldrich. Alexa Fluor 594 was bought from Molecular Probes. Tryptone was obtained from VWR Scientific. HTTP Isopore (0.4 μm pore diameter) membrane filters were purchased from Millipore.

Fabrication of Microfluidic Devices.

Microfluidic devices were manufactured by using soft lithographic techniques as described (14, 15). Briefly, glass masters with the features shown in Fig. 1 were fabricated by etching soda lime glass coated with a lithographically patterned photoresist (S1813, Shipley, Houston) and used to make molds of polydimethylsiloxane (PDMS; Dow-Corning Sylgard Silicone Elastomer-184, Krayden, Marlborough, MA). Holes, which served as inlets and outlets, were reamed through the top of the PDMS molds by using syringe needles. A planar borosilicate coverslip was brought into conformal contact with the PDMS after oxygen plasma treatment for 15 s (plasma cleaner PDC-32G, Harrick Scientific, Ossining, NY).

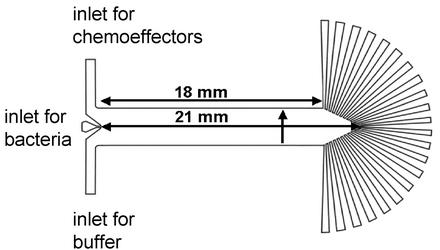
Figure 1.

Device for microfluidic chemotaxis assays. The main channel is 18 mm long at the edge and 21 mm long in the center. Its height is 8 μm. The bacterial inlet is 151 μm wide, each buffer inlet is 1.51 mm wide, and the total width of the channel is 3.18 mm. The width of each outlet port at its junction with the main channel is 200 μm. The vertical arrow indicates the direction of increasing chemoeffector concentration across the channel.

Gradient profiles of the devices were probed by injection of an Alexa Fluor 594 dye and a 5(6)-carboxyfluorescein dye into the two reagent inlets separately while a suspension of bacteria with an OD₅₄₀ of 0.7 (3–4 × 10⁸ cells per ml) was infused into the middle inlet. Dye concentrations were determined from the fluorescence intensities of both dyes recorded across the channel by using a charge-coupled device camera mounted on top of an inverted fluorescence microscope (TE 2000, Nikon).

Monitoring Chemotaxis in the Microfluidic Device.

Single colonies from E. coli strains RP437, SW10, MM509, VB13, MM5000, and RP3098 containing plasmid pBJC100 were grown overnight in tryptone broth (TB; 10 g/liter tryptone, 8 g/liter NaCl, and 50 μg/ml ampicillin) at 32°C. To induce expression of GFP, 50 μl of the overnight culture was added to 5 ml of TB containing arabinose at a final concentration of 0.002% (wt/vol) and grown at 32°C with agitation to an OD₅₄₀ of 0.7. The cultures were drawn through HTTP filters (0.4 μm pore size) and washed three times with equal volumes of chemotaxis buffer (10 mM physiological buffered saline, pH 7.0, containing 0.1 mM EDTA, 0.01 mM l-methionine, and 10 mM d-lactate). The bacteria were resuspended in 1 ml of chemotaxis buffer and kept at room temperature until use.

Chemoeffectors and buffer, respectively, were injected through the two reagent ports by using 500-μl Hamilton syringes. The resuspended bacteria were introduced through the middle port from a 50-μl syringe. The size of the middle inlet was 10 times smaller than the outer inlets, which kept the flow velocity approximately equal through each inlet. Syringes were controlled with a Harvard Apparatus PHD 2000 syringe pump modified with a 100:1 gear reducer designed for continuous pumping at an extremely low volume of flow (<1 nl/min). A total flow rate of 314 nl/min was maintained in the main channel during experimental runs without significantly disturbing the flow pattern. Ten minutes after pumping began, 120 time-lapse images were taken at regions immediately upstream from the outlets by using a ×10 objective with 200-ms exposures and 1-s intervals between each picture. A computer program (J. M. B. Manson, personal communication) was used to automatically count the bacteria that passed through the imaged region. After 35 min, bacteria stuck to the floor and wall of each outlet port were counted in photographic images taken at ×100 magnification.

Results

Rationale for a Microfluidic Chemotaxis Assay.

Fluids moving in micrometer-scale channels have properties that often do not exist on the macroscopic scale. For example, flow inside a microchannel is laminar, with Reynolds' numbers of 1 or less. Thus, when two liquid streams flow next to each other, the only mixing that occurs is by molecular diffusion (16, 17). This property has been used to create defined gradients of chemoeffectors sensed by neutrophils (18) or neurons (19). The microfluidic assay described below uses this property as its central operating principle (Fig. 1).

The device contains three inlets (left side of Fig. 1). Chemoeffector solutions are introduced through the upper inlet, buffer through the lower. A concentration gradient develops perpendicular to the direction of flow. The slope of the gradient, monitored with fluorescent dyes, was six times as steep immediately downstream of the inlets as it was in the region immediately upstream of the outlets.

A third, narrower inlet between these two streams is used to inject E. coli cells (rods 2–4 μm long by 0.7 μm in diameter). The cells encounter the evolving chemical gradient as they move downstream. The gradient changes along the length of the channel, but it remains constant at any given point. At the far end (right side of Fig. 1) each cell enters one of 22 outlets according to the direction and extent of its migration normal to the direction of flow.

The velocity of bulk fluid flow down the channel is the average flow rate divided by the cross-sectional area, or (0.000314 cm³/min)/(0.0008 cm × 0.318 cm) = 1.23 cm/min. The time to reach the end of the channel is the length of the channel divided by the bulk flow rate, or 2.1 cm/1.23 cm/min = 1.71 min. If a cell moves with the bulk flow, it should take 1.71 min (102 s) to transit the device.

Cells were visualized by inducing synthesis of GFP from the plasmid pBJC100 (Table 1) with 0.002% (wt/vol) arabinose during growth. All of the cell counts presented here were obtained by using a fluorescence microscope to count the GFP-labeled cells that accumulated within each outlet port through nonspecific sticking to its floor and walls. We have since developed a computer-tabulation method that records the number of cells moving past any point from the inlet to the outlet. The program produces a histogram in which the number of cells in bins of any desired size is plotted versus cross-sectional position in the channel. Direct comparison of the two methods indicates that they yield the same distribution of cells if the images analyzed by the computer are taken just upstream of the outlets (data not shown).

Behavior of Cells in the Absence of Gradients.

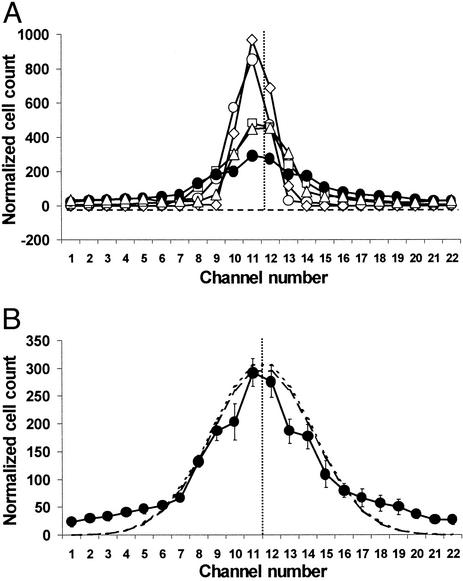
Fig. 2 shows the distributions of cells for five strains tested in the absence of chemotactic gradients: WT, an aspartate-blind Δ(tar-tap) mutant, a receptorless mutant deleted for all transducers except aer, a nonmotile but flagellated ΔmotAB mutant, and a strain lacking all flagellar and chemotaxis gene products. Based on qualitative microscopic examination, the fraction of motile cells and their swimming speeds were similar before and after passage through the device, indicating that cells that did not stick permanently within the channel suffered no substantial loss of motility during their journey.

Figure 2.

Distribution of cells in the absence of gradients. Cells were grown as described. Cells of motile strains swam vigorously at the time of harvesting. (A) Washed cells in chemotaxis buffer were introduced into the microfluidic device and counted as described. The number of cells counted in each outlet port is given. The total number of cells was normalized to the mean number (2,105) of cells counted during seven runs with the WT strain. WT cells (●), aspartate-blind cells (▵), receptorless cells (□), flagellated, nonmotile cells (◊), and nonflagellated cells (○). The horizontal line with short dashes shows the no-cell baseline, and the vertical dotted line marks the middle of the device, corresponding to outlet 11.5. (B) The distribution of WT cells (from A), with error bars. In seven trials the standard error in the counts for well populated channels was <10%. The standard error across all outlets was ≈20%. The line with long dashes represents the best-fit Gaussian curve (σ = 3.6) for WT cells, and the line with short dashes represents the curve calculated for the case of diffusion from an extended source of limited extent (20). Note that there is little difference between the latter and the normal curve.

Nonflagellated cells took an average of 101 ± 17 s (n = 6, longest 124 s, shortest 84 s) to travel the 2.1 cm from the inlet to outlets 11 and 12, the same time required for bulk liquid flow (102 s). Nonmotile cells with flagella and WT motile cells had transit times of 155 ± 33 s (n = 24) and 152 ± 31 s (n = 21), respectively. The variation in transit times may be caused by unequal braking effects on individual cells based on the time they spend transiently stuck to the floor or ceiling of the channel. Cells with flagella, whether motile or not, take ≈50% longer to move down the channel, consistent with their having more contact with the surfaces.

The nonmotile and nonflagellated cells were both distributed tightly, although the distribution for the nonflagellated cells had wider tails. The distributions for the receptorless, aspartate-blind, and serine-blind strains were of intermediate breadth, and that of the WT strain was the widest. The receptorless cells do not spread rapidly because they swim in gentle curves that loop back on themselves. Dispersal of aspartate-blind and serine-blind cells may be low relative to WT cells because of a run/tumble ratio less conducive to random dispersal.

The distribution of the WT cells was not Gaussian; more cells remained in the middle of the channel than predicted for a normal distribution, and the tails were more extended. At least three factors could contribute to this departure from the ideal case. First, the cells were injected in a stream 151 μm wide; their distribution must therefore be calculated as diffusion from an extended source of limited extent (20). Second, by the time they arrived at the end of the channel, some of the cells reached the side walls of the channel and thus did not behave as if they were dispersing into an infinite space. Finally, individual cells swim at different speeds and have different run/tumble biases (21). Reconstruction modeling demonstrates that a mixture of normally distributed populations with different variances does not generate a Gaussian distribution (M. Longnecker, personal communication).

With these caveats in mind, we empirically determined a best-fit Gaussian curve for the WT cells. The standard deviation was ±3.6 channel widths, or ±0.52 mm (±3.6/22 × 3.18 mm). Fig. 2B compares this normal curve with the distribution of WT cells and also shows the curve calculated for diffusion from an extended source of limited extent by using σ = 3.6. It differs little from the normal curve because the bacterial inlet is relatively narrow and the time needed for the bacteria to traverse the channel is relatively long (≈150 s).

Responses to Attractants and Repellents.

The Tar receptor mediates attractant responses to l-aspartate and repellent responses to Ni²⁺. The distributions of WT cells at three different concentrations of aspartate and Ni²⁺ are shown in Fig. 3 A and B, respectively. Even 3.2 nM l-aspartate was sufficient to skew the distribution toward the side of the channel on which it was introduced. This bias was larger at 10 nM and still greater at 1 mM. With Ni²⁺ no response was noted at 10 μM, but a strong bias away from 1 mM Ni²⁺ was observed. Cells did not move as far when the input Ni²⁺ concentration was increased to 10 mM. We presume that 10 mM Ni²⁺ inhibited motility, because at 32 mM Ni²⁺ (data not shown) the cells remained in a tight distribution at the center of the channel, indistinguishable from that shown by nonmotile cells (Fig. 2).

Figure 3.

Responses of WT cells to attractant and repellent. (A) Normalized cell counts were determined as in Fig. 2 for: 3.2 nM l-aspartate (▵), 10 nM l-aspartate (□), and 1 mM l-aspartate (◊). (B) Normalized cell counts for: 10 μM Ni²⁺ (▵), 1 mM Ni²⁺ (□), and 10 mM Ni²⁺ (◊). The curve with long dashes shows the normal distribution in the presence of buffer (Fig. 2B). The vertical line with short dashes marks the middle of the device.

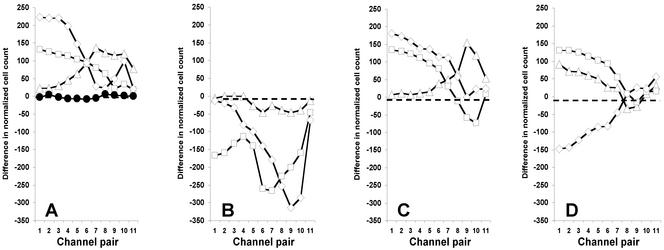
Asymmetry of Cell Distribution Patterns.

The cell counts in Fig. 3 give a qualitative feel for the responses to aspartate and Ni²⁺, but we desired a clearer representation of the asymmetry of the distributions. Also, the nonmotile or nonresponsive cells could obscure the response. We thus performed a difference calculation by subtracting the cell count for the rightmost channel (no. 22) from that for the leftmost channel (no. 1), the count for channel 21 from that for channel 2, etc., for responses of WT cells to l-aspartate (Fig. 4A), Ni²⁺ (Fig. 4B), l-serine (Fig. 4C), and l-leucine (Fig. 4D). These plots show the sign and magnitude of the cell migration patterns. The flat line at 0 for the difference plots of cells in buffer (Fig. 4A) shows that this treatment cancels out the contributions of nonmotile and nonresponsive cells.

Figure 4.

Differential response of WT cells to attractant and repellent. Difference calculations are described in the text. (A) Difference in normalized cell counts in the presence of l-aspartate: buffer only (●), 3.2 nM (▵), 10 nM (□), and 1 mM (◊). (B) Difference in normalized cell count for WT cells in the presence of Ni²⁺: 10 μM (▵), 1 mM (□), and 10 mM (◊). (C) Difference in normalized cell count for WT cells in the presence of l-serine: 1 μM (▵), 1 mM (□), and 10 mM (◊). (D) Difference in normalized cell count in the presence of l-leucine: 1 μM (▵), 100 μM (□), and 10 mM (◊).

Calculation of Partition and Migration Coefficients.

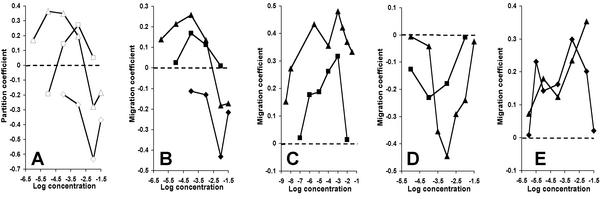
The difference curves in Fig. 4 were used to determine what fraction of the cells moved to one side of the chamber. Because cell counts were normalized for each assay, we simply added the differences in cell number (Fig. 4) and divided by the total number of cells. This calculation yields a number between 1 and −1 that we call the chemotaxis partition coefficient (CPC). A CPC of 1 indicates that all cells go to the side on which an attractant was introduced, and a CPC of −1 indicates that all cells go to the side of the channel away from that on which a repellent was introduced. A value of 0 indicates no net response. Fig. 5A presents a plot of CPC values for l-leucine at all concentrations tested.

Figure 5.

CPC and CMC values for WT and mutant cells. WT cells (▴), serine-blind cells (■), and aspartate-blind cells (⧫). (A) CPC with l-leucine. (B) CMC with l-leucine. (C) CMC with l-aspartate. (D) CMC with Ni²⁺. (E) CMC with l-serine.

One parameter not taken into account in the CPC is how far the cells migrate from the middle of the channel. Also, the random noise of the signal is greatest near the middle of the channel, yet all difference calculations are given equal weight. To avoid these shortcomings, we performed another calculation in which the difference counts are weighted by the fractional distance of the channels from the center. For example, the difference count for the channel 1-22 pair is multiplied by 10.5/10.5 = 1.00, the difference count for the channel 2-21 pair is multiplied by 9.5/10.5 = 0.905, etc. The sum of these values was divided by the total normalized cell count. This calculation again yields a number between 1 and −1 that we call the chemotactic migration coefficient (CMC). A CMC of 1 indicates that all cells go to channel 1 (strongest attractant response), a value of −1 indicates that all cells go to channel 22 (strongest repellent response), and a value of 0 indicates no net response. CMC values for WT cells at all tested concentrations of l-leucine, l-aspartate, Ni²⁺, and l-serine are shown in Fig. 5 B–E.

Behavior of Chemoreceptor Mutants.

A biphasic response to l-leucine (attractant at low concentrations, repellent at high concentrations) was clear when the data were expressed as CPC or CMC values. To determine the basis of this phenomenon, we compared the responses of WT cells to l-leucine with those of serine-blind, aspartate-blind, and receptorless cells. We also tested these cells with l-aspartate, l-serine, and Ni²⁺. The CPC and CMC values are given in Fig. 5. The receptorless cells produced a tight, symmetrical distribution in each case (data not shown). Cells of the serine-blind mutant did not respond to l-serine (CPC and CMC values <0.01), and cells of the aspartate-blind mutant did not respond to l-aspartate or Ni²⁺.

The aspartate-blind and serine-blind mutants generally yielded lower CPC values and still lower CMC values than did WT cells with the compounds to which they could respond. This result is consistent with the lower random motility of the mutant cells (Fig. 2). Finally, the CPC and CMC values of the mutants showed that the response of WT cells to l-leucine is biphasic because leucine is sensed at low concentrations by Tar as an attractant and at higher concentrations by Tsr as a repellent.

Discussion

The classic method for measuring chemotaxis is the capillary assay developed by Pfeffer in the late 19th century and standardized by Adler (22) 30 years ago. The assay is simple, the results are remarkably reproducible, and the gradients generated by diffusion of a capillary have been mathematically characterized (23, 24). However, the concentration gradient in the capillary assay becomes shallower over time until it finally disappears, and the relatively low numbers of cells that are exposed to a detectable concentration gradient limit its sensitivity.

In the microfluidic assay, the bacteria are injected into the steepest part of the gradient. The gradient they encounter changes as flow proceeds downstream, but the chemoeffector concentration at each position along the channel remains at steady state because the solutions are constantly replenished in the laminar-flow environment. Thus, each bacterium that follows a similar path experiences identical concentration patterns. The microfluidic assay also has the advantage that a high signal-to-noise ratio is achieved, because every cell is counted, including those that swim toward higher or lower concentrations and those that do not migrate at all. The capillary assay is binary; cells either swim into the capillary or do not. Finally, because the distribution of cells can be analyzed by video recording at any position along the microfluidic channel, the assay can be used to determine the speed with which the cells migrate in gradients.

The advantage of the microfluidic assay is greatest at low (e.g., nanomolar) attractant concentrations or with repellents. In the capillary assay, only a small subset of the population of cells in the “pond” is exposed to a detectable gradient if the capillary contains nanomolar levels of chemoeffector. The lowest concentrations of the potent attractants l-aspartate and l-serine that generate a statistically significant response with E. coli are ≈1 μM (22). In contrast, we can detect responses with initial aspartate concentrations as low as 3.2 nM (Fig. 3).

The repellent-in-pond assay for negative chemotaxis is insensitive (9, 25) because only a few bacteria are exposed to gradients that they can detect. Repellents also diffuse into the capillary to nullify the gradient. The geometry of the microfluidic assay suggests that responses to repellents should be as robust as those to attractants, a prediction that holds true for l-leucine and Ni²⁺.

Other assays for bacterial chemotaxis exist. The swarm-plate assay (3, 4), which applies only to metabolizable attractants, yields primarily qualitative, yes-or-no answers. The tethered cell assay (26) requires time-consuming observation of videotapes or often unreliable motion analysis and does not measure responses to gradients. Temporal assays of swimming cells (27) share most of the limitations of the tethered cell assay.

Among the more specialized assays, the automated cell tracker (28) provided the first detailed information about the behavior of individual swimming cells. However, it can follow only one cell at a time, and it requires highly sophisticated data recording equipment. Other assays include observation of cells in osmotically stabilized spatial gradients (29), in arrays of glass capillaries (30), and in a stopped-flow diffusion chamber (SFDC) (31). Recently, the bacterial transport coefficients measured with the capillary and SFDC assays have been compared quantitatively (32). Using E. coli strain AW405 at 24°C, a good correspondence was found for the bacterial transport coefficients for the attractant α-methylaspartate over the range of 0.01 to 1 mM. These two assays and single-cell tracking also yielded similar random motility coefficients (see below). We will calibrate our method to these assays, using the analogs α-methylaspartate and α-aminoisobutyric acid to avoid any complications caused by metabolism of aspartate and serine, once we automate our data analysis and solve the problem with sticking cells. However, the microfluidic assay in its current form already provides quantitative and reproducible data, and it outperforms the capillary assay for quantifying repellent responses.

Our assays were done at room temperature, but temperature can be controlled by running coolant through tubes embedded in the polydimethylsiloxane polymer (33). The device and protocol can readily be modified to monitor aerotaxis, thermotaxis, phototaxis, or magnetotaxis, and any sufficiently small swimming microorganism can be examined, even nonculturable bacteria in environmental samples. Depending on the counting procedure adopted, an assay can be run in as little as 10 min, and a number of devices can be serviced in parallel by a single pump. The device should also be usable to select or enrich for mutants that are defective in a tactic response or that respond to novel compounds, or to monitor competition between strains with seemingly equal chemotactic capabilities.

Our device may also be useful for characterizing random motility in bacteria. For example, we can calculate the random motility constant μ_o (32) of WT cells from the standard deviation (σ) of the best-fit normal curve in Fig. 2 by using the equation σ = (2 μ_ot)^1/2 (34). Thus, μ_o = σ²/2t, where t is the transit time for cells through the channel. Substituting 0.052 cm for σ and 152 s for t yields μ_o = 8.9 × 10⁻⁶ cm²/s. This value falls directly in the middle of the 100-fold range of values of μ_o (1–100 × 10⁻⁶ cm²/s; see table 2 in ref. 32) determined in various ways for different E. coli strains over the past 35 years.

The preliminary experiments reported here simply demonstrate a proof of concept. However, some biological insights were gained. First, we found that WT cells disperse better than cells lacking one or both of the major receptors Tar and Tsr (Fig. 2). Second, the low concentration of l-aspartate (3.2 nM at the inlet) that generated a significant migration of RP437 WT cells was impressive (Figs. 3A, 4A, and 5C). Finally, the discovery that l-leucine acts as an attractant sensed by Tar and as a repellent sensed by Tsr (Fig. 5 A and B) surprised us. Although these results may possess only modest significance, they herald a series of new insights awaiting discovery.

Abbreviations

CPC

chemotaxis partition coefficient

CMC

chemotactic migration coefficient