Modular organization of internal models of tools in the human cerebellum

Abstract

Human capabilities in dexterously manipulating many different tools suggest modular neural organization at functional levels, but anatomical modularity underlying the capabilities has yet to be demonstrated. Although modularity in phylogenetically older parts of the cerebellum is well known, comparable modularity in the lateral cerebellum for cognitive functions remains unknown. We investigated these issues by functional MRI (fMRI) based on our previous findings of a cerebellar internal model of a tool. After subjects intensively learned to manipulate two novel tools (the rotated mouse whose cursor appeared at a rotated position, and the velocity mouse whose cursor velocity was proportional to the mouse position), they could easily switch between the two. The lateral and posterior cerebellar activities for the two different tools were spatially segregated, and their overlaps were <10%, even at low statistical thresholds. Activities of the rotated mouse were more anterior and lateral than the velocity mouse activities. These results were consistent with predictions by the MOdular Selection And Identification Controller (MOSAIC) model that multiple internal models compete to partition sensory-motor experiences and their outputs are linearly combined for a particular context.

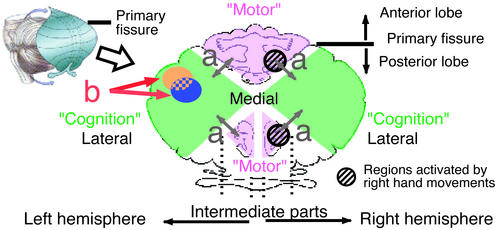
Structural and functional modularity is an important key to understanding brain and mind mechanisms. Much is known about the modular architecture in the primary cerebral cortex. Somatotopic organization in the sensory-motor cortices is a well known modular feature (1). Regarding the cerebellum, Snider and Eldred (2) recorded surface potentials evoked by peripheral stimuli and presented somatotopic maps in cats and monkeys, where one map lay in the anterior lobe and the other lay in the intermediate parts of the posterior lobe (Fig. 1). Recently, by using functional MRI (fMRI), Grodd et al. (3) investigated activation patterns in the human cerebellum during motor tasks and found two homunculoid representations similar to those found by Snider and Eldred (2). These somatotopic maps show modularity on a relatively large scale. Functional modularity on a fine scale has also been studied in these regions. Regarding parallel fiber inputs, somatotopic maps have been identified in the cerebellar cortex, but the map is fractured, that is, each small area of body surface is represented multiple times by spatially separated clusters of cells (4, 5). Microzones, as long as several centimeters along the longitudinal axis of the cerebellar folia and as wide as 0.2 mm, have been identified for climbing fiber inputs as functional units (6).

Figure 1.

Flattened view of cerebellar surface illustrating that anterior lobe and intermediate parts of posterior lobe are related to “motor and somatosensory functions,” whereas lateral posterior cerebellum is related to “cognitive functions.” (a) Arrows indicate difference between “motor” and “cognition” found in previous neuroimaging studies. (b) Arrows indicate modularity within lateral posterior cerebellum for two different cognitive functions. Illustrations were modified from refs. 39 and 40.

The above cerebellar modularity has been demonstrated only for motor and somatosensory functions. In the past decade, a growing number of studies revealed that the cerebellum contributes to higher cognitive functions. One of the first examples during a clearly cognitive task came from studies of language processing and reported activation in the right lateral cerebellum (7, 8). Since then, other studies (for reviews, see refs. 9 and 10) have also pointed to cerebellar involvement in cognitive tasks such as working memory (11), problem solving (12, 13), and visual attention (14). Many studies (11, 14, 15) demonstrated that cognitive and motor (somatosensory) processing independently activate distinct cerebellar regions: the former activates the lateral part of the posterior lobe, and the latter activates the anterior lobe and the intermediate parts of the posterior lobe, where the homunculoid representations lie (Fig. 1a, arrows). Although this dichotomy is not deterministic, convergent evidence in functional imaging studies suggests that the lateral part of the posterior lobe is closely related to the cognitive functions.

Regarding cognitive functions in the lateral cerebellum, studies performing metaanalysis of published data suggested that there is anatomical distribution of activity related to different tasks (10, 16). However, it has not been resolved whether each area might uniquely contribute to a distinct cognitive function. Hence, modularity has yet to be experimentally demonstrated for the “cognitive” cerebellum (Fig. 1b, arrows).

Recent computational models such as MOdular Selection And Identification Controller (MOSAIC) (17–20) suggest that multiple internal models reside in the cerebellum. Internal models are neural mechanisms that can mimic the input–output properties of motor apparatuses or their inverses (21–23). This motor control theory can be extended to a cognitive domain, i.e., use of tools, by simply extending the object of internal model learning from motor apparatuses (objects of motor control) to a general object in the external world. In our previous study, we found that an internal model for a novel tool is acquired in the cerebellar cortex while human subjects learn to use the tool (24). Here, we investigate modularity and multiplicity of internal models in cerebellar cortex after subjects learn to switch between two different novel tools.

Methods

Subjects.

Seven neurologically normal subjects (21–32 years of age; five females and two males) participated in the experiments. All subjects were right-handed except for one left-handed participant (25). Informed written consent was obtained from each participant. The protocol was approved by the ethics committees of Communications Research Laboratory and Advanced Telecommunications Research Institute.

Tasks.

All subjects, including the one left-handed subject, manipulated a computer mouse with the right hand to track a randomly moving target on a screen with a cursor (a tracking task). By changing the transformation, i.e., from mouse movement to cursor movement, we generated two novel tools: the rotated mouse and the velocity mouse. The relationship between the cursor position and the mouse position was

for the rotated mouse, where (x_c, y_c) denotes the cursor's screen coordinates (visual angle, °), and (x_m, y_m) denotes the mouse/hand coordinates (centimeters). In contrast, the cursor's velocity (ẋ_c, ẏ_c) (°/second) was determined by the mouse position for the velocity mouse:

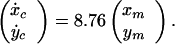A projector controlled by a personal computer displayed the target and the cursor. A small white square target was presented on a dark background. The x and y components of the target path were each sums of sinusoids whose amplitude and frequency were randomly determined. The subjects moved a small crosshair cursor on the screen with the mouse.

The subjects were given detailed verbal instructions about the transformation. The color of the cursor (red, violet, or green) and text presented on the screen (“rotate,” “velocity,” or “normal”) indicated the current tool.

Training Sessions.

Seven subjects performed 18 training sessions before fMRI scanning. The sessions were divided into 2 days (14 sessions on Day 1). The tasks were performed outside of the MRI scanner, but the subjects lay as in the scanner. In each session, the subjects performed the tracking task by using the two novel mice and a normal mouse, six times each in blocks of 43.2 s. The order of the mice (1. rotated 2. normal 3. velocity or 1. velocity 2. normal 3. rotated) was counterbalanced between sessions. The subjects had a rest period in every fourth block, which also lasted 43.2 s. Therefore, a training session lasted 17.28 min [ = 43.2 s × 6 repetitions × (three tools + rest)].

Scanning Sessions.

All subjects underwent four fMRI scanning sessions after the training sessions. Each session comprised 16 alternating blocks (one block, 43.2 s) of test and baseline periods and lasted 11 min and 31 s (= 43.2 s × eight repetitions × two tools). In two of the four sessions, the subjects manipulated the rotated mouse during the test periods and the normal mouse during the baseline periods (“rotated session”). In the other two sessions, the subjects manipulated the velocity mouse during the test periods and the normal mouse during the baseline periods (“velocity session”). The session order was counterbalanced between subjects. By increasing the target velocity during the baseline periods, the errors during the baseline periods were matched to those during the test periods according to the methods explained below (see Equalization of Tracking Error). Five of the seven subjects performed the supplementary scanning experiment in which they manipulated the three kinds of mice in a single session. Each session was the same as the training session except that the error was equalized (see below).

Equalization of Tracking Error.

In our previous study (24), two types of activity related to the learning were observed in the cerebellum. One reflected the error signals guiding the learning acquisition of the internal models, and the other reflected an acquired internal model. The former activity was very strong and distributed over the cerebellum and also blurred the latter activity. Following a procedure used in the previous study, tracking error during manipulation of one mouse was equalized to another by using a linear relationship between a tracking error and a target velocity. This procedure allowed us to distinguish internal model activity for the novel tools from activity reflecting the error signal.

Before the functional imaging, the subjects performed the tracking task by using each mouse (the normal, the rotated, or the velocity mouse) at various target velocities for 15 min. A linear relationship was derived by the least-squares method. In the first scanning experiment, the target velocity was increased in the baseline period by using this relationship, so that the baseline error was equal to the mean error in the preceding test period. In the supplementary experiment, the order of the tools was 1. rotated 2. normal 3. velocity or 1. velocity 2. normal 3. rotated, and the errors for the second and third tools were matched to the mean error for the first tool. The details of this method are described in ref. 24.

MRI Acquisition.

MRI scanners (1.5 T) were used to obtain blood oxygen level-dependent contrast functional images. Images weighted with the apparent transverse relaxation time were obtained with an echo-planar imaging sequence (repetition time, 5.4 s; echo time, 66 ms; flip angle, 90°; field of view, 256 × 256 mm; matrix size, 64 × 64). Twenty-two axial slices (thickness, 4 mm) encompassing the cerebellum were selected. One hundred twenty-eight or 192 functional images were scanned for each slice during one session in the first or the supplementary experiment, respectively. High-resolution anatomical images were obtained for these slices with a T₁ weighted sequence.

Analysis of Behavior Data.

The cursor and the target positions were sampled at 60 Hz. Mouse positions were reconstructed from the cursor positions afterward. Each subject's performance was measured by the tracking errors, i.e., the average distance between the cursor and the target. The distance between the cursor and the target at each sampling point was accumulated over 5.4 s (position tracking error). The mouse velocity or the target velocity was also accumulated over 5.4 s, and this was used as an explanatory variable in the regression analysis of the brain activity.

MRI Analysis.

Motion artifacts were removed by using automated image registration (http://bishopw.loni.ucla.edu/AIR3). We used SPM99 (www.fil.ion.ucl.ac.uk/spm) for further analysis. The functional images of each subject's cerebellum were transformed to the Montreal Neurological Institute's (MNI; Montreal, Canada) reference brain. The data were spatially smoothed with a Gaussian kernel with an 8-mm full width at half maximum (FWHM). The voxel time series were temporally smoothed with a Gaussian filter (FWHM of 4 s).

A Model for Simple Subtraction Analysis.

For the comparison between each novel mouse and the normal mouse, condition-specific effects were estimated with a linear model:

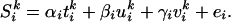Here, S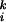 denotes the fMRI signal at the ith voxel in the kth scan. t, u, and v were explanatory variables representing the type of mouse used (t, rotation, u, velocity; and v, normal). Each was a step function assigned 1 if the scan corresponded to its mouse type and 0 otherwise. e is a residual error. Session-specific effects were also modeled as effects of no interest. Activations related to the rotated mouse and the velocity mouse were specified by statistical comparisons of the estimated parameters (α > γ for rotation and β > γ for velocity) by using t statistics (Statistical Parametric Mapping{t}).

A Model for Multiple Regression Analysis.

We also conducted a multiple regression analysis including explanatory variables corresponding to various behavioral factors. The linear model was:

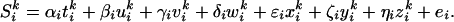As described above, the first three variables were step functions of the mouse type. w represented switching of a mouse and was assigned 1 in the scan immediately after the mouse type changed and 0 otherwise. x, y, and z were the mouse velocity, tracking error, and target velocity, respectively. They were recorded during the scans and averaged over a scan interval (5.4 s). Mouse velocity is related to mouse and/or hand movements, and the target velocity is related to visual motion information and attention. Activations related to the rotation and the velocity mice were specified by the statistical comparisons: α > γ and β > γ. Activations related to the last four variables were specified by finding regions where the estimated parameters (δ, ɛ, ζ, and η) were significantly larger than zero.

We used the effective degree of freedom adjusted for analysis of fMRI (26). In assessing statistical significance, we made a correction for multiple comparisons based on the theory of random Gaussian fields. This correction was made for the entire volume of the cerebellum.

Results

Behavioral Results During Training Sessions.

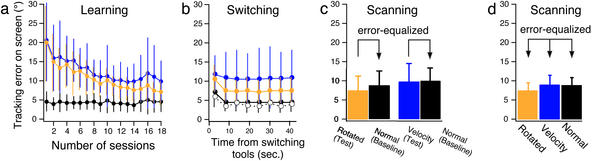
For the rotated and velocity mice, the tracking errors decreased significantly as the number of sessions increased (Fig. 2a, orange or blue line), suggesting that learning occurred. A repeated-measures ANOVA on the errors indicated a significant effect of sessions for the rotated mouse [F(17, 102) = 21.32, P < 0.0001] and for the velocity mouse [(F(17, 102) = 14.90, P < 0.0001]. In contrast, for the normal mouse, the errors were small and constant (black line). There was no significant effect of sessions for the normal mouse [F(17, 102) = 0.53].

Figure 2.

(a) Tracking errors (across-subjects, mean ± SD) when subjects manipulate rotated mouse (orange line), velocity mouse (blue line), and normal mouse (black line) in training sessions. (b) Time course of errors (across-subjects, mean ± SD) in last five training sessions aligned on switching of tools. Broken line with open circles indicates time course obtained from a control experiment, in which the cursor position was reset to center but the tool did not change and was always the normal mouse. (c) Tracking errors (across-subjects, mean + SD) when cerebellar activity was scanned in the first experiment. Error during manipulation of rotated mouse or velocity mouse was matched by changing target velocity during manipulation of normal mouse (baseline). Baseline error matched to rotated mouse was significantly larger than corresponding test error [F(1, 6) = 15.52, P < 0.01]. There was no significant difference in errors between velocity mouse and corresponding baseline [F(1, 6) = 0.45]. (d) Tracking errors (across-subjects, mean + SD) in the first and the supplementary scanning experiments. There was no significant difference between any pair of mean values according to Tukey's honestly significant difference method (at P < 0.05 level).

The tracking errors aligned on the switching of the tools (Fig. 2b), averaged over the subjects and the last five sessions, were almost constant after the switching, indicating that the subjects rapidly switched internal models appropriate for the different tools. Although a repeated-measures ANOVA on the errors indicated a significant effect of the time after the switching for the rotated mouse [F(7, 42) = 17.45, P < 0.0001] and the normal mouse [F(7, 42) = 20.24, P < 0.0001], only the error during the first 5.4 s after the switching was significantly larger than the other errors (at the P < 0.05 level by Tukey's honestly significant difference method). The transient error increase was most probably induced by reset of the cursor position to the center of the screen when a tool changed. We conducted a control experiment where the cursor was reset to the center but the tool did not change and found a very similar time course of the error (the broken line with open circles in Fig. 2b). The behavioral data strongly suggest that internal models are acquired as separate functional modules.

Comparison of Activation Patterns Between Each Novel Mouse and the Normal Mouse.

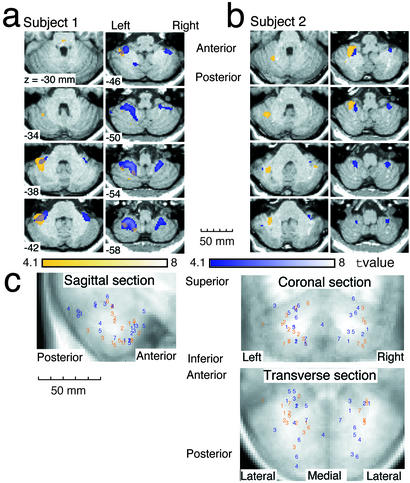
The colored regions in Fig. 3a (subject 1) and Fig. 3b (subject 2) indicate regions significantly more activated during the test periods than the baseline periods [t (236) > 4.1, fixed effect model, P < 0.05 corrected]. The orange and blue regions indicate activity for the rotated mouse and the velocity mouse, respectively. Fig. 3c shows the four local maxima with the highest activity for each subject [t maps; t (236) > 3.1, P < 0.001 not corrected] derived from a comparison of the test periods with the baseline periods for all subjects. Here, the colors indicate the tools (orange = rotated, blue = velocity), and the numbers indicate subjects. The rotated mouse activations tend to be located more anteriorly and laterally than the velocity mouse activations. A multivariate ANOVA on the 3D positions of the local maxima (anterior–posterior, inferior–superior, and lateral–medial) revealed this significant positional difference [F(2, 41) = 3.54, P < 0.05]. Significant increase in activity in the test periods cannot be attributed to the tracking error, the mouse/hand movements, the visual target velocity, attention, or effort, because the magnitudes of these factors in the baseline periods were larger than those in the test periods as described below.

Figure 3.

(a and b) Cerebellar activity of two typical subjects in transverse sections. Colored regions were significantly more activated in test periods than in baseline periods (P < 0.05 corrected for multiple comparisons in the cerebellum). Orange and blue regions were activated in rotated and velocity sessions, respectively. Overlap between orange and blue was activated in both sessions. Numbers in bottom left corners of images indicate superior–inferior (z) positions in Montreal Neurological Institute's coordinates (see Methods). (c) Distributions of four local maxima with highest activity (P < 0.001 not corrected) for each subject. Orange and blue numbers indicate maxima in rotated sessions and velocity sessions, respectively. Positions of maxima and normalized anatomical images are projected onto transverse, coronal and sagittal sections. Numbers correspond to different subjects.

Fig. 2c shows the tracking errors averaged across the subjects. In the rotated session, the baseline error was significantly larger than the test error [F(1, 6) = 15.52, P < 0.01], whereas in the velocity session, there was no significant difference between the test and the baseline errors [F(1, 6) = 0.45]. These results suggest that the above activation revealed by the test minus the baseline contrast does not reflect error signals.

To check whether the activation was evoked by behavioral factors other than the error, we investigated the kinematics (velocity and acceleration) of the cursor and the mouse/hand movements (see also Supporting Text and Table 2, which are published as supporting information on the PNAS web site, www.pnas.org). In any comparison between the test and baseline periods, the velocity and acceleration in the baseline periods were significantly larger than those in the test periods [F(1, 6) > 63.7, P < 0.0002; about 1.5-fold for velocity and 2-fold for acceleration]. Because the force is proportional to the acceleration, dynamic factors in the baseline periods are also expected to be larger than those in the test periods. The target velocity and acceleration are closely related to visual motion and eye movements. They were large in the baseline periods in comparison to those in the test periods [F(1, 6) > 22.4, P < 0.003], suggesting that the magnitudes of the visual motion and eye movements were larger in the baseline periods. All of the subjects reported that they needed more effort and attention in the baseline periods than in the test periods because of the increased target velocity. Thus, the activation increase in the test periods cannot be attributed to the mouse/hand movements, the visual motion, the eye movements, attention, or effort. The most plausible explanation is that the activity increase in the test periods reflects the acquired internal model for the novel tools.

Table 1 shows a summary of activation. The activated volume was measured in each subject's activity map and then averaged. The overlapping region is only 2.1% of the total activated volume by using a moderate threshold (P < 0.05 corrected) and 6.3% even at a considerably lower threshold (P < 0.001 uncorrected). The sizes of the orange (57.5%) and blue (40.4%) regions are comparable at the moderate threshold. The different tools evoked activities in distinct locations with small overlap, demonstrating the modularity and multiplicity of internal models for tools.

Table 1.

Percentage of activated volume to total activated volume (%) and absolute activated volume (cm³, in parentheses) averaged over all subjects

Region*	Color codes in Figs. 3 and 4	R-(R ∩ V) orange	V-(R ∩ V) blue	R ∩ V overlap
Threshold	P < 0.001 corrected (t > 5.0)	75.7 (6.36)	24.1 (2.03)	0.2 (0.02)
	P < 0.05 corrected (t > 4.1)	57.5 (9.22)	40.4 (6.46)	2.1 (0.34)
	P < 0.001 uncorrected (t > 3.1)	45.4 (13.82)	48.3 (14.70)	6.3 (1.9)

^*R-(R ∩ V) or V-(R ∩ V) was activated only when subjects manipulated rotated mouse or velocity mouse, respectively. R ∩ V was activated when subjects manipulated either rotated mouse or velocity mouse. 

We also measured activated volume (P < 0.05 corrected) in the left and the right sides of the cerebellum for each subject. The averaged volume was 5.76 cm³ in the left side and 3.79 cm³ in the right side for the rotated mouse, whereas it was 3.24 and 3.56 cm³ for the velocity mouse. Activation was bilateral in general, but a preference for the left side was observed in the rotated-mouse activity.

Results of Multiple Regression Analysis.

As described above, the activation increase in the test periods cannot be attributed to behavioral factors (i.e., tracking error, mouse/hand movements, visual motion, eye movements, attention, or effort). However, we have to justify our assumption that the difference in activation patterns obtained from the simple subtraction analyses solely reflects the regional differences in the internal models. This is because the error-equalization procedure inevitably increases the magnitudes of the behavioral factors in the baseline periods, and the level of this increase depends on the tracking error during use of the novel mice. Use of the normal mouse at different levels of these factors may change the baseline activation patterns and may affect the results of the subtraction analysis.

Because it is impossible to simultaneously equalize every aspect of a subject's behavior, we decided to conduct an additional analysis by using a multiple regression technique to remove possible factors that may affect the cerebellar activity, i.e., tool switching, hand/mouse movements, tracking error, visual motion, and eye movements (see Methods). Using a linear model of brain activity including these factors and the type of mouse as explanatory variables, we can estimate the unadulterated effect associated with the use of each mouse. Large variability and a large data set are necessary for a reliable multiple regression analysis. Thus, we conducted a supplementary experiment with a different design from the previous one (see Methods) and then combined the data from the previous and the supplementary experiments.

There was no significant difference in the tracking error among the mice, as shown in Fig. 2d (at P < 0.05 level by Tukey's honestly significant difference method), because the tracking errors for the three kinds of mice were equalized by changing the target velocity.

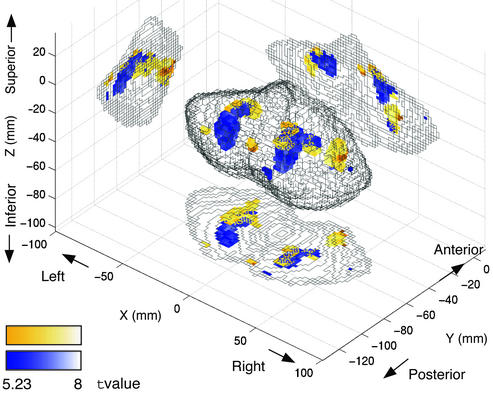
To specify the activation related to use of the novel tools, by using t statistics, we compared the parameters estimated for the above explanatory variables corresponding to mouse type. The orange (or the blue) regions in Fig. 4 indicate voxels where the parameter for the rotated mouse (or the velocity mouse) was significantly larger than the parameter for the normal mouse [t(7,113) > 5.23, fixed effect model, P < 0.001 corrected; see also Movies 1–8, which are published as supporting information on the PNAS web site]. The relative locations of the two tools averaged across subjects (i.e., anterior and lateral for rotated mouse) were very similar to those in Fig. 3 for individual subjects.

Figure 4.

Regions related to manipulation of the novel tools as revealed by multiple regression analysis. Regions are shown in superior–posterior–lateral view (Center), lateral view from right side (Left), superior view (Bottom), and posterior (Right) view. Orange and blue colors indicate regions where activation was more highly and positively correlated with manipulation of rotated or velocity mouse, respectively, than manipulation of normal mouse. Statistical thresholds are P < 0.001 corrected.

Activations related to the other explanatory variables were specified by finding regions where the estimated parameters were significantly larger than zero (the same threshold as above). Activations correlated with tool switching were in bilateral superior parts of the cerebellum (anterior lobule). The peaks of switching activation in Montreal Neurological Institute's space (x, y, z, respectively) and their t values were (−22, −82, −18; t = 15.16) in the left hemisphere and (28, −74, −18; t = 10.92) in the right hemisphere. Activations correlated with the mouse average velocity, that is, directly correlated with movement control, were in the anterior lobule (24, −54, −28; t = 13.52) and the biventer lobule (24, −60, −56; t = 7.52) ipsilateral to the hand that was used. This is consistent with the previous study (3) indicating somatotopic organization for sensory-motor functions. Only weak activity related to the tracking error was observed in the lateral parts of the cerebellum at low thresholds (P < 0.05 not corrected; −50, −68, −26; t = 1.66), because the tracking error was constant by experimental design (Fig. 2d). Activity related to the average target velocity (visual motion information and eye movements) did not reach significant levels in the cerebellum even with a low threshold.

The error-equalization procedure increased magnitudes of hand/mouse movements and other behavioral factors in the baseline periods and may have affected the activation patterns in the previous analysis. However, the multiple regression analysis of the combined data from the previous and supplementary experiments demonstrated similar activation patterns to the previous analysis even when several possible factors were taken into account. These results together demonstrate that somewhat common cerebellar areas are allocated for each tool across all subjects, although there exist large interindividual differences at exact locations (Fig. 3c).

Discussion

Integration of Multiple Internal Models.

The MOSAIC theory (17) proposes that multiple pairs of controllers (inverse internal models) and predictors (forward internal models) are tightly coupled as functional units. They contribute to the selection of appropriate modules for the current behavioral situation. The key feature is a “responsibility signal” calculated for each module. The forward model generates a prediction of the outcome of the motor commands being issued. The prediction is confirmed by the sensory consequences. The smaller the prediction error, the more likely that the pair of forward and inverse models must have been appropriate for the current situation, and hence the higher the module's responsibility. The responsibility signals determine the degree of each module's contribution to the total output from the cerebellum. Because each responsibility signal is an analog value, the linear combination of multiple modules' outputs is possible. By modulating and combining the output, an enormous repertoire of behaviors can be generated even if the number of modules is limited (20). Many situations that we encounter may be derived from a combination of previously experienced situations, that is, the same modules may be activated in different situations.

Our results were consistent with the theory in two points. First, activation related to a specific novel tool was observed in multiple regions (Figs. 3 and 4), which suggests that multiple modules are combined to cope with the tool. Second, small but significant common regions were activated by different tools (Table 1). This suggests that the internal models acquired in these regions represent common properties with the novel mice. It is not likely that they were related to the hand movements or the normal mouse because they were found by subtraction of the activation for the normal mouse from the activation for the novel mouse.

Number of Microzones Contributing to Internal Models of the Novel Tools.

Each forward or inverse model may correspond to a microzone from a neurophysiological viewpoint. Using two different methods, we estimated the number of microzones that constitute internal models of the novel mice. In the first simple method, we estimated the activated microzones based on the ratio of the activated volume to the cerebellar volume and the numbers of microzones contained in the human cerebellum. According to Table 1, the mean activated volume is 9.22 cm³ for the rotated mouse only and 6.46 cm³ for the velocity mouse only at the medium threshold (P < 0.05 corrected). Human cerebellar volume of healthy adults is about 130 cm³ (27), which contains 5,000–10,000 microzones (28). Thus, the estimated numbers are 355–709 (= 5,000 or 10,000 × 9.22/130) for the rotated mouse and 298–497 (= 5,000 or 10,000 × 6.46/130) for the velocity mouse. This estimation gives the upper bounds, because we assume that microzones are densely packed into fMRI voxels and neglects any blurring effects by the spatial smoothing filter used in the analysis.

The other, more reasonable, method is based on the anatomical size of the microzone and considers how a microzone's activity was blurred by our imaging resolution and the smoothing filter. The size of the microzone along the cerebellar folia ranges between 5 and 12 mm in humans (3), with a width of 0.2 mm (6) and a cortical thickness of 1 mm (29). Accounting for our imaging resolution (4-mm isotropic voxels), one microzone activates three voxels (length × width × thickness: 3 × 1 × 1 voxels). Because we spatially smoothed the image with a Gaussian filter having an 8-mm full width at half maximum, the activity could spread maximally over the adjacent 14 voxels. As mentioned above, the mean activated volume was 9.22 cm³ for the rotated mouse and 6.46 cm³ for the velocity mouse at the medium threshold. The volumes of 3 and 17 voxels are 0.192 cm³ and 1.088 cm³. We estimated the number of microzones by dividing the activated volume by the volume corresponding to one microzone, i.e., 9 (= 9.22/1.088) − 48 (= 9.22/0.192) for the rotated mouse, and 6 (= 6.46/1.088) − 34 (= 6.46/0.192) for the velocity mouse.

This estimation assumes that microzones related to a similar function are sparsely distributed. If these microzones are densely packed in each voxel, the estimated number of microzones increases. However, it is unlikely that neighboring microzones behave similarly, which is against the definition of a microzone (i.e., different climbing fiber inputs and hence different functions). Although there is a large variability in the estimated numbers, a small portion of all microzones (about 10% at maximum) is related to each novel mouse.

Multiple Internal Models for Cognitive Functions.

For the following reasons, we believe that internal models acquired in the current experiment are for cognitive functions rather than basic sensory-motor transformations. First, the acquired internal models in these experiments are expected to represent the relationship between the cursor movement and the “mouse” movement rather than the “hand” movement. This is because our previous behavioral study (30) found that the learning effects in this task are not specific to the hand, that is, the effects acquired during practice by using one hand can be easily carried over to performance by using the other hand. Second, the bilateral activity may indicate that activated regions acquire internal models for cognitive functions independent of the ipsilateral correspondence between the motor apparatus and the cerebellum (e.g., refs. 11, 13–15, 31). Regarding the rotated-mouse activation, a preference for the left side, i.e., contralateral to the performing hand, was observed and agrees with activity related to cognitive spatial operations (e.g., maze learning, ref. 15).

Anatomical and physiological studies in monkeys demonstrated connectivity between the lateral cerebellum and the frontal and parietal cortices (32–34). Our previous study (35) investigated the entire brain activity when human subjects learned to use the rotated mouse. We revealed that functional connectivity between the loci of the lateral cerebellum examined in this study and the ventral premotor cortex (especially the right homologue of Broca's area) increased after sufficient learning. These cerebral regions could provide inputs and read outputs from the internal models acquired in the cerebellum. For example, mirror neurons in the ventral premotor cortex (36) may have input–output relationships with internal models and may represent the desired state of action.

Many functional imaging studies using a variety of paradigms with pictures and words have reported tool-related regions (for a review, see ref. 37): the medial fusiform gyrus activated by form of tools, the left posterior middle temporal gyrus representing visual motion related to tool use, and the ventral premotor regions representing tool-use-associated action. The concept of tool is complex, and semantic memory of tools consists of information stored in these distributed networks. Current study suggests that the cerebellum also contributes to the representation of tool by storing information about the input–output property of each tool. We confirmed this by showing differences in cerebellar activation patterns between common tools such as a hammer and a knife (38).

Although trends common to all subjects could be identified in the spatial distributions of the rotated mouse modules (anterior–lateral) and the velocity mouse modules (posterior–medial) (Fig. 4), their precise locations differed among the subjects (Fig. 3c). This may indicate that locations of internal models for cognitive functions are not innately determined. This characteristic in the lateral posterior “cognitive” cerebellum contrasts strikingly with the low variability of somatotopic organization in the “motor” cerebellum (3), the anterior lobe, and the intermediate parts of the posterior lobe. The somatotopic organization directly correlated with physical systems that are common to humans, whereas the functional modules in higher cognition may differ among individuals with different cultural and conventional backgrounds.

We demonstrated anatomical modularity in the cognitive cerebellum with multiple internal models for different tools. Although the MOSAIC theory was originally proposed in studies of motor control, our results suggest that the computational architectures proposed by the theory may be common to the “cognitive” and “motor” cerebellum.

Abbreviation

fMRI

functional MRI