Symmetry breaking in individual plasmonic nanoparticles

Abstract

The plasmon resonances of a concentric metallic nanoshell arise from the hybridization of primitive plasmon modes of the same angular momentum on its inner and outer surfaces. For a nanoshell with an offset core, the reduction in symmetry relaxes these selection rules, allowing for an admixture of dipolar components in all plasmon modes of the particle. This metallodielectric nanostructure with reduced symmetry exhibits a core offset-dependent multipeaked spectrum, seen in single-particle spectroscopic measurements, and exhibits significantly larger local-field enhancements on its external surface than the equivalent concentric spherical nanostructure.

The optical properties of metallic nanostructures are a topic of considerable scientific and technological importance. The optical properties of a metallic nanoparticle are determined by its plasmon resonances, which are strongly dependent on particle geometry. The structural tunability of plasmon resonances has been one of the reasons for the growing interest in a rapidly expanding array of nanoparticle geometries, such as nanorods (1, 2), nanorings (3), nanocubes (4, 5), triangular nanoprisms (6–8), nanoshells (9), and branched nanocrystals (10, 11). The resonant excitation of plasmons can lead to large local enhancements of the incident electromagnetic field at the nanoparticle surface, resulting in dramatically large enhancements of the cross section for nonlinear optical spectroscopies such as surface-enhanced Raman scattering (12–16). The structural dependence of both the local-field and far-field optical properties of nanoparticles across the visible and near-infrared (NIR) spectral regions has enabled their use in a wide range of biomedical applications, an area of increasing importance and societal impact (17–21).

Metallic nanoshells, composed of a spherical dielectric core surrounded by a concentric metal shell, support plasmon resonances whose energies are determined sensitively by inner core and outer shell dimensions (9). This geometric dependence arises from the hybridization between cavity plasmons supported by the inner surface of the shell and the sphere plasmons of the outer surface (22, 23). This interaction results in the formation of two hybridized plasmons, a low-energy symmetric or “bonding” plasmon and a high-energy antisymmetric or “antibonding” plasmon mode. The bonding plasmon interacts strongly with an incident optical field, whereas the antibonding plasmon mode interacts only weakly with the incident light and can be further damped by the interband transitions in the metal (24). For a spherically symmetric nanoshell, where the center of the inner shell surface is coincident with the center of the outer shell surface, plasmon hybridization only occurs between cavity and sphere plasmon states of the same angular momentum, denoted by multipolar index l (Δl = 0). In the dipole, or electrostatic limit, only the l = 1 dipolar bonding plasmon is excited by an incident optical plane wave (25). However, when the center of the inner shell surface is displaced with respect to the center of the outer shell surface, cavity and sphere plasmons of all multipolar indices mix and contribute to the bonding and antibonding plasmon modes of the “nanoegg” geometry with reduced symmetry. As a consequence, all plasmon modes of this structure can be optically excited, even in the dipole limit.

Here we present an experimental investigation and theoretical analysis of the effect of the symmetry breaking on the plasmon modes of this metallodielectric nanostructure. As the offset between the center of the inner and outer shell surfaces is increased, the optical spectrum broadens and includes additional peaks adjacent to the original dipolar plasmon resonance. Reduced-symmetry nanoegg structures were fabricated experimentally based on the anisotropic deposition of additional metallic Au onto previously fabricated silica–Au concentric nanoshells. The experimentally obtained optical spectra of the individual nanostructures clearly show this characteristic offset-dependent multipeaked spectrum. Calculations of the local electromagnetic field reveal that reduction of symmetry is accompanied by large electromagnetic field enhancements on the surface of the nanostructure, significantly larger than those obtainable for the concentric nanoparticle case.

Results and Discussions

The plasmon hybridization method can be used to describe the plasmonic properties of this structure under reduced symmetry (22, 23). The conduction electrons are considered to be a charged, incompressible liquid of uniform density on top of a rigid, positive charge representing the ion cores. The ion cores are treated within the jellium approximation, so the positive background charge is assumed to be uniformly distributed within the particle’s boundaries. Plasmon modes are self-sustained deformations of the electron liquid. Because the liquid is incompressible, the only electromagnetic effect associated with such deformations is the appearance of surface charges (26, 27).

A nanoshell with a dielectric core of radius a displaced a distance D from the center of an outer shell of radius b can be denoted (a, b, D) and is schematically illustrated as an extension of the spherically symmetric nanoshell geometry in Fig. 1A Inset. The conduction electron density in the shell is assumed to be uniform n₀ corresponding to a bulk plasmon frequency

For simplicity, in Fig. 1, we assume a vacuum core and neglect the polarizability of the positive background of the metal. The deformation field can be expressed as a gradient of a scalar potential η (23), which takes the form:

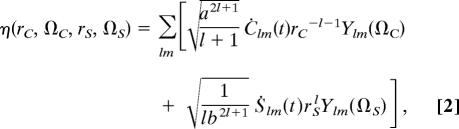where (r_C, Ω_C) are spherical coordinates centered in the cavity, and (r_S, Ω_S) are spherical coordinates with an origin at the center of the spherical outer shell. The quantities of C_lm and S_lm are the amplitudes of the primitive cavity and sphere plasmons, respectively. For finite offset D, the spherical harmonics centered on the two different origins are no longer orthogonal for different l, resulting in interactions between the cavity and sphere modes in a manner analogous to the coupling between the individual nanoparticle plasmons of a nanoparticle dimer or in periodic structures of metallic nanoparticles in close proximity (28–30) As in the case of nanoparticle dimers, the azimuthal index m remains conserved.

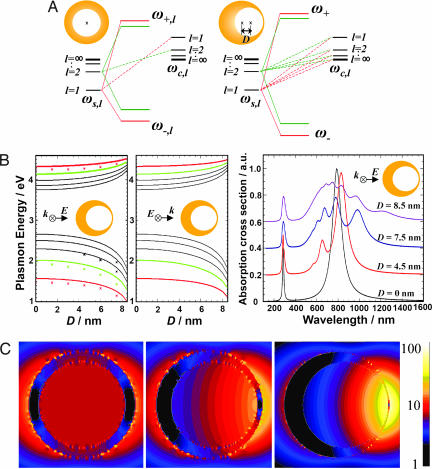
Fig. 1.

Electromagnetic properties of nanoshells with a nonconcentric core. (A) Schematic of plasmon hybridization in a nanoshell (Left) and a nonconcentric nanoshell, or nanoegg (Right). (B) (Left) Calculated l = 1–5 plasmon energies as function of core offset D for parallel polarization (solid line, plasmon hybridization; dots, FDTD). (Center) Perpendicular polarization. (Right) Theoretical absorption spectra as a function of offset D obtained by the plasmon hybridization method, for an [r₁, r₂] = 39, 48 nm Au nanoshell with vacuum core. (C) Near-field plots of [r₁, r₂] = 39, 48 nm Au nanoshells with different offset cores (silica) and an empirically based dielectric function for Au. (Left) D = 0 nm at λ = 641 nm. (Center) D = 4.5 nm at λ = 663 nm. (Right) D = 7.5 nm at λ = 743 nm. Maximum field enhancements |E|/|E₀| are 13.2 (Left), 25.2 (Center), and 60.3 (Right). The incident field is horizontally polarized.

The Lagrangian for this system can be constructed directly from η. The structure of the resulting eigenvalue problem is illustrated in Fig. 1A. The cavity plasmons have energies

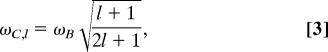and the sphere plasmons have energies

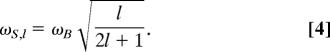Fig. 1A Left shows the resulting plasmon modes for a spherically symmetric nanoshell. The interaction is diagonal in multipolar index lm, where both bonding and antibonding nanoshell plasmon modes are formed for each lm. The plasmon energies depend on multipolar index l but not on the azimuthal index m, which labels the 2l + 1 possible orientations of the plasmon modes. For finite offset D (Fig. 1A Right), an interaction exists between all cavity and sphere modes of the same m. This interaction leads to stronger hybridization and an admixture of all primitive cavity and sphere plasmons in the plasmon modes of the reduced-symmetry nanostructure. For simplicity, we will refer to these reduced symmetry nanoparticle plasmon modes by multipolar index l, corresponding to the spherical or zero offset case, although for finite offset the plasmon modes contain an admixture of plasmons of all l for a given m. For the nonconcentric nanoshell, the coupling of the cavity and sphere plasmons depends on azimuthal m, but the resulting plasmon energy spectrum is only weakly dependent on orientation. In Fig. 1B Left and Center, we show the shifts in the plasmon modes deriving from the nanoshell l = 1–5 bonding and antibonding plasmon modes as a function of increasing offset D, for the two orthogonal polarizations of incident light excitation. The figure shows a strong redshift of the bonding and blueshift of the antibonding plasmon modes with increasing D. Here we also see that the plasmon modes for the two principal polarization axes evolve with increasing offset in an extremely similar fashion. In Fig. 1B Left, we have also plotted the plasmon resonances obtained by a peak extraction from the extinction spectra calculated by using the finite difference time domain (FDTD) method. The FDTD method is a powerful numerical approach that has recently been shown to be highly useful in the study of the electromagnetic properties of metallic nanostructures of almost arbitrary complexity (31–36). The FDTD simulations show geometry-dependent plasmon energy shifts, which are in good agreement with the conceptually simpler and more intuitive picture provided by the plasmon hybridization approach. In Fig. 1B Right, we show the theoretical optical absorption spectra for various offset values D for an incident polarization direction corresponding to Fig. 1B Left. As D increases, the l = 1 mode is redshifted, and the higher l modes, now dipole active, contribute additional peaks to the spectrum, increasing in complexity with increasing D. In Fig. 1C, we show the electric field enhancements calculated using the FDTD method for nanoeggs with a silica core with the metallic shell modeled using the empirically obtained dielectric function for Au (37). The calculation shows very large field intensity enhancements, of magnitudes comparable with those attainable in nanoparticle dimer junctions (35) and fabricated bowtie nanoantennas (38). However, in contrast to those geometries, here the region of maximum field enhancement is located on the open, exterior surface of an individual nanostructure and not within a narrow confined gap or junction.

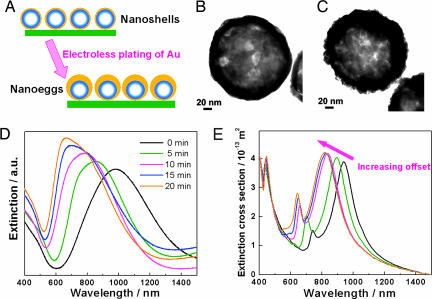
Nanoshells with an offset core can be experimentally fabricated by using an anisotropic electroless plating technique (Fig. 2A). Concentric Au nanoshells were fabricated following a reported method using silica nanospheres as the core (9) and were immobilized onto poly(4-vinylpyridine) (PVP)-functionalized glass substrates as a dispersed monolayer of isolated nanoshells (39). The nanoshell films were subsequently immersed in an aqueous solution containing appropriate amounts of HAuCl₄ and K₂CO₃, where the addition of formaldehyde then initiated the electroless plating of Au onto the nanoparticle surfaces. The films were subsequently removed from the plating solution, rinsed, and dried. As a result, all of the nanoeggs fabricated in this manner have the same orientation on the glass slides, with the point of contact with the glass substrate corresponding to the minimum in shell thickness for each nanoparticle. Increasing the time duration of the plating process results in an increase in the effective core offset of each nanoegg particle. Fig. 2 B and C shows typical transmission electron microcopy (TEM) images of a concentric nanoshell with homogenous shell thickness of 9 nm and a nanoegg with a core offset of 10 nm, respectively. In Fig. 2D, we show the evolution of the extinction spectra of the oriented nanoegg films as a function of electroless plating time. These measurements were performed on nanoegg films by using normal incidence, unpolarized light. The spectral envelope of the plasmonic features shifts to shorter wavelengths as the electroless plating time increases. This trend is in good agreement with FDTD calculations (Fig. 2E), which also show a spectral peak blueshift with increasing core offset, for the same orientation of core offset with respect to incident light. In these ensemble measurements, the plasmon peaks are significantly and asymmetrically broadened in comparison with the calculated spectra, because of the distribution in sizes and offsets in the fabricated nanostructures.

Fig. 2.

Synthesis of nanoshells with a nonconcentric core. (A) Schematic of nanoegg fabrication. Monolayers of silica–Au core–shell nanoparticles were first immobilized on PVP-functionalized glass slides. The nanoshells used in this set of experiments are 94 ± 9 nm in core radius and 9 ± 1 nm in shell thickness. By controlling the reaction time, the offset extent can be controlled. Longer reaction time results in the formation of nanoeggs with larger offset cores. (B and C) TEM images of a nanoshell (B) and nanoegg (C). (D) Experimentally measured evolution of extinction spectra of oriented monolayer nanoegg film during metallization with unpolarized optical excitation at normal incidence. (E) Calculated normal incidence extinction spectra (FDTD) of reduced symmetry nanoparticles as a function of increasing offset. In this set of calculations, the nanoeggs have a silica core of 94 nm in radius. The thinnest part of the shell is 9 nm, and the thickest part of the shell is 9 nm for concentric nanoshell and varied to be 15, 21, 27, and 33 nm for nanoeggs.

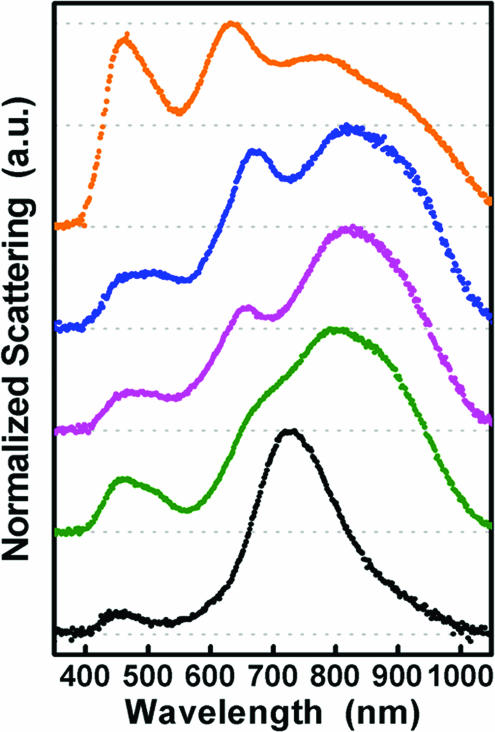
To further investigate the evolution of the plasmon energies of these reduced symmetry nanostructures, we performed dark-field spectroscopic measurements on isolated, individual, randomly oriented nanoeggs in reflection mode. A sequence of single particle spectra is shown in Fig. 3. The lowest spectrum is that of a single nanoshell, accompanied by representative spectra of reduced symmetry nanoparticles, each displaced vertically for clarity. The sequence of spectra shown with increasing vertical displacement corresponds to that of increasing offset D. The nanoshell bonding plasmon is seen at 730 nm and is accompanied by a much smaller broad peak at nominally 450 nm corresponding to the antibonding plasmon. For reduced symmetry nanoparticles, we see the onset and development of multipeaked spectra of increasing complexity, accompanied by an overall redshift of the spectral envelope. Additionally, the antibonding plasmon peak becomes broader and eventually quite large, of similar magnitude as the accompanying lower energy modes in the nanoparticle spectrum. The peak positions and lineshapes vary significantly as the core offset changes. These single-particle spectra bear a striking qualitative resemblance to the theoretically calculated spectra shown in Fig. 1B. The presence of a dielectric substrate, the dark-field optical excitation and collection geometry, and phase-retardation effects (40) may affect the spectral widths observed for the experimentally fabricated nanoparticles relative to the theoretical spectra in Fig. 1B. Within experimental error, the fabricated nanoparticles have effective core offsets around D = 3.3 nm and therefore correspond exactly to the regime where additional hybridized peaks should appear in the theoretical spectra. A direct analysis of the experimental spectra is needed and requires detailed modeling of the effect of the substrate, the effect of nanoparticle orientation, and the particular scattering geometry of our microscope.

Fig. 3.

Normalized single-particle dark-field scattering spectra of a nanoshell (black curve; [r₁, r₂] = [94, 103] nm) and four different reduced-symmetry nanoparticles (colored spectra). Nanoeggs were fabricated by electroless plating of Au onto the exposed surfaces of deposited nanoshells, to a maximum Au thickness of ≈25 nm. Selected unpolarized spectra of individual nanoparticles show that the fabrication process produces structures with a distribution of core offsets.

Conclusions

In conclusion, we have shown that symmetry breaking can strongly modify the selection rules for the interaction of plasmon modes on an individual nanoparticle. This finding has profound consequences for the optical spectrum of the particle, allowing all plasmon modes to possess some dipolar character and contribute to additional features in the optical spectrum as symmetry is reduced. For concentric nanoshells, reduction in symmetry also is accompanied by an increased electromagnetic field enhancement on its external surface, located at the narrowest region of shell thickness. This approach may be useful in analyzing and understanding the local- and far-field optical response of other reduced-symmetry nanostructures of even greater complexity and, ultimately, in the design of various nanoparticle geometries with specific near-field optical properties.

Materials and Methods

Tetraethyl orthosilicate (TEOS; 99.9999%), (3-aminopropyl)trimethoxysilane (APTMS), tetrachloroauric acid (HAuCl₄), and PVP (160,000 MW) were purchased from Sigma-Aldrich. Ammonium hydroxide, potassium carbonate (K₂CO₃), and ethanol were purchased from Fisher Scientific. Ultrapure water (18.2 MΩ resistivity) was obtained from a Milli-Q water purification system (Millipore). Glass microscope slides were obtained from Gold Seal Products (Portsmouth, NH). All of the chemicals were used as received without further purification.

Concentric silica core–Au shell nanoparticles were fabricated following a reported seed-mediated electroless plating method (9) and then were immobilized onto PVP-functionalized glass substrates as a monolayer of isolated nanoshells (39). The nanoshells used in the present work were 94 ± 9 nm in core radius and 9 ± 1 nm in shell thickness. Nanoshells with an offset core can be experimentally fabricated using an anisotropic electroless plating technique by immersing the nanoshell films in 9 ml of aqueous solution containing 1 mM HAuCl₄ and 3.5 mM K₂CO_3, where the addition of 20 μl of 37% formaldehyde then initiated the electroless plating of Au onto the nanoparticle surfaces. The films were subsequently removed from the plating solution after a certain period of reaction time, rinsed with ethanol, and dried with nitrogen gas flow. All of the nanoegg particles fabricated in this manner have the same orientation on the glass slides, with the point in contact with the glass substrate corresponding to the minimum shell thickness for each nanoegg particle. Increasing the reaction time of the plating process increases the effective core offset of the nanoeggs.

The morphologies and ensemble optical properties of the products were characterized by scanning electron microscope (SEM), TEM, and UV-visible (vis)-NIR spectroscopic measurements. SEM images were obtained on a Philips FEI XL-30 environmental SEM at an acceleration voltage of 30 kV. TEM images were obtained by using JEOL JEM-2010 TEM. The extinction spectra were measured by using a Cary 5000 UV-vis-NIR spectrophotometer (Varian) in the wavelength range of 400–1,500 nm.

Dark-field single particle spectroscopic measurements were performed by using an inverted microscope (Zeiss Axiovert 200 MAT). A reflection dark-field objective (100×, numerical aperture 0.9) was used to focus the image of each single nanoparticle at the entrance slit of a spectrograph (SP-2165; Acton Research, Acton, MA), and data were collected with a charge-coupled device array (PhotonMax 512; Princeton Instruments, Trenton, NJ). For these measurements, a sample of nanoeggs was prepared where, after fabrication, the immobilized nanoparticles were removed from the substrate and released into an aqueous solution by application of an ultrasonic probe. The nanostructures then were dispersed by spin-coating onto a PVP-coated glass substrate. Spectra were all acquired in ambient air. The spectrum of an area of the sample containing no nanoparticles was subtracted from the nanoparticle spectrum for background correction, and the nanoparticle spectra were divided by a white-light calibration standard spectrum (Edmund Optics, Barrington, NJ) to correct for any possible wavelength-dependent variations in collection efficiencies in the system.

Abbreviations

FDTD

finite difference time domain

NIR

near-infrared

TEM

transmission electron microcopy

PVP

poly(4-vinylpyridine).