Cellular asymmetry and individuality in directional sensing

Abstract

It is generally assumed that single cells in an isogenic population, when exposed to identical environments, exhibit the same behavior. However, it is becoming increasingly clear that, even in a genetically identical population, cellular behavior can vary significantly among cells. Here we explore this variability in the gradient-sensing response of Dictyostelium cells when exposed to repeated spatiotemporal pulses of chemoattractant. Our experiments show the response of a single cell to be highly reproducible from pulse to pulse. In contrast, a large variability in the response direction and magnitude is observed from cell to cell, even when different cells are exposed to the same pulse. First, these results indicate that the gradient-sensing network has inherent asymmetries that can significantly impact the ability of cells to faithfully sense the direction of extracellular signals (cellular asymmetry). Second, we find that the magnitude of this asymmetry varies greatly among cells. Some cells are able to accurately follow the direction of an extracellular stimulus, whereas, in other cells, the intracellular asymmetry dominates, resulting in a polarization axis that is independent of the direction of the extracellular cue (cellular individuality). We integrate these experimental findings into a model that treats the effective signal a cell detects as the product of the extracellular signal and the asymmetric intracellular signal. With this model we successfully predict the population response. This cellular individuality and asymmetry might fundamentally limit the fidelity of signal detection; in contrast, however, it might be beneficial by diversifying phenotypes in isogenic populations.

The low number of molecules involved in biological systems can lead to large stochastic effects and population heterogeneity even within a genetically identical population (1–3). For example, the swimming behavior of Escherichia coli cells varies greatly from cell to cell (4), and recent studies start to link this variability in swimming behavior to concentration fluctuations in regulatory proteins (5–7). It is an open question whether a similar variability can be observed in eukaryotic chemotactic cells, such as the slime mold Dictyostelium discoideum, which has the exquisite ability to sense and respond to shallow gradients of chemoattractants. In these spatially sensitive systems, signaling errors might be introduced in two different ways. First, the concentrations of intracellular signaling components might vary from cell to cell; second, spatial inhomogeneities or asymmetries in the cellular distributions of molecules might influence the ability of cells to sense slight spatial differences in the extracellular environment.

To explore this question, we employ a quantitative approach to systematically study directional sensing in single Dictyostelium cells. Recent experiments have demonstrated that an extracellular signal induces spatial localization of several signaling proteins along the plasma membrane (8–12). The localization of these molecules at the membrane allows a cell to polarize and move in the direction of the external signal. We quantitatively monitored the spatial and temporal localization of one of the key signaling proteins fused to GFP, which provides a convenient reporter of directional sensing at the single cell level.

Upon exposure to the same extracellular signal, the GFP localization varies greatly from cell to cell, whereas a single cell will repeatedly give the same response. We find that the difference in response between the single cell and population is due to asymmetries internal to each cell. Furthermore, this asymmetry varies in magnitude from cell to cell, causing some cells to accurately follow a moving stimulus, whereas others do not. Although we find that most cells are strongly asymmetric in their response, previous experimental and modeling studies have focused mainly on explaining the response of symmetric cells. Because the asymmetry can have a significant impact on the ability of cells to sense external gradients, we developed a model that combines intracellular asymmetries with extracellular signals. When combined with measured parameters, the model is able to accurately predict the observed population response.

Results and Discussion

Starved Dictyostelium cells were immobilized and seeded into an observation chamber containing a known concentration of caged cAMP. The response of cells to a short pulse of cAMP was quantified by monitoring the spatial and temporal localization of the cytosolic regulator of adenylyl cyclase (CRAC) fused to GFP (8–11). The CRAC–GFP fusion retains the wild-type activity (12). During stimulation, the pleckstrin homology domain of CRAC binds to the phospholipid phosphatidylinositol 3,4,5-triphosphate [PI(3,4,5)P₃], causing CRAC–GFP to translocate to the leading edge of the cell. The GFP fluorescence along the cell membrane therefore provides a reporter of directional sensing at the single cell level (12–16). A spatiotemporal cAMP gradient was formed by uncaging a known concentration of cAMP with a circular UV beam (Fig. 1a). The cAMP gradient was quantified by numerically integrating the diffusion equation in an infinite, two-dimensional chamber (Supporting Text and Fig. 6, which are published as supporting information on the PNAS web site). A major advantage of using a caged compound is the ability to reproduce the exact same spatiotemporal gradient repeatedly, which allows us to measure the variability of the response of a single cell to multiple identical cAMP pulses.

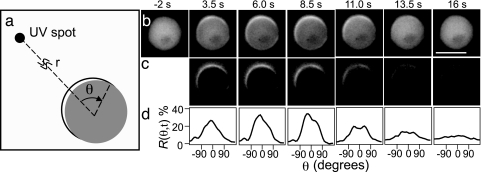
Fig. 1.

Dynamic translocation of CRAC–GFP at the plasma membrane after stimulation with a 2-s pulse of cAMP. (a) The UV uncaging location is positioned a distance r away from the cell center. The angle θ defines the coordinate along the cell’s periphery, where θ = 0 defines the position at the membrane that is closest to the uncaging location. (b) Unprocessed epifluorescence images displaying CRAC–GFP as a function of time. The scale bar denotes 10 μm and r = 70 μm. (c) Subtracted images illustrate the relative change of CRAC–GFP concentration in the membrane with respect to the prestimulus level (t = −2 s). (d) Response function R(θ,t) as a function of time for the images in c.

Fig. 1b illustrates the dynamic translocation of CRAC–GFP to the membrane after stimulation with a 2-s UV pulse for a cell with a depolymerized actin cytoskeleton. Directional sensing does not require cell motility or morphological changes (12, 17, 18). Therefore, immobilized cells provide the advantage of studying directional sensing in the absence of the more complex downstream responses, such as changes in cell shape. The relative CRAC–GFP concentration in the membrane with respect to the prestimulus level was measured by subtracting the images taken after the release of the stimulus from the image taken just before the release of the stimulus (Fig. 1c). We defined a response function, R(θ, t), to quantify the relative CRAC–GFP concentration in the membrane. To determine R(θ, t), first the cell membrane was segmented in 20 subregions. Second, the difference between GFP intensity at time t and at t = 0 (just before uncaging) is computed for each of the 20 subregions. Finally, we correct for the cell-to-cell variability in GFP levels by normalizing R(θ, t) by the average cytoplasmic GFP fluorescence at t = 0 available to each subregion (1/20th of the total cytoplasmic GFP fluorescence). This ratio defines the response function R(θ, t). For example an R(θ, t) value at 100% for all 20 segments implies that every available CRAC–GFP molecule has been recruited to the membrane. However, 10 adjacent subregions having an R(θ, t) value of 100% and the remaining 10 subregions having an R(θ, t) value of 0% implies that 50% of the total cytoplasmic CRAC molecules have been recruited to 10 subregions. Conversely, an R(θ, t) value of 0% for a specific segment means that the CRAC–GFP concentration in the membrane is identical before and after cAMP uncaging. Fig. 1d displays R(θ, t) for the cell depicted in Fig. 1c. R(θ, t) shows a clear polarized response that is most pronounced ≈8 s after uncaging.

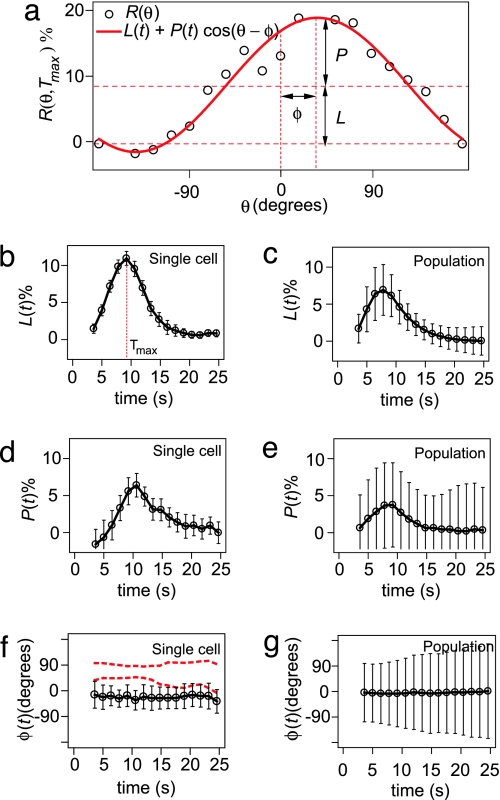
We have characterized R(θ, t) with three parameters: localization, L; polarization, P; and polarization angle, φ. These three parameters are determined by fitting the experimentally obtained response function R(θ, t) with R_fit(θ, t) = L(t)+P(t)cos[θ − φ(t)] (Fig. 2a). Fig. 2 displays the dynamics of L, P, and φ for a single cell (Fig. 2 b, d, and f) and a population of 40 cells (Fig. 2 c, e, and g). After stimulation with a pulse of cAMP, L and P increase and reach a maximum value, followed by a return to their prestimulus level in≈30 s. The time at which L reaches its maximum is defined as T_max. For a single cell, φ remains more or less constant during the response time (Fig. 2f). The error bars on the single-cell data reflect the variability from pulse to pulse, which is significantly smaller than the variability from cell to cell, denoted by the error bars on the population data. Taken together these data suggest that when a single cell is repeatedly stimulated with identical pulses, it responds in a highly reproducible manner. From pulse to pulse, a single cell recruits a very similar average CRAC–GFP concentration to the membrane [reflected in L(t)] and creates a very similar CRAC–GFP gradient at the membrane [reflected in P(t)], and this gradient is oriented in the same direction from pulse to pulse [reflected in φ(t)]. However from cell to cell, a large variability is observed in these three parameters.

Fig. 2.

Definition of localization, L, polarization, P, and polarization angle, φ, and a comparison between the time dependence of these parameters for a single cell (which is stimulated 10 times) and a population of 40 cells (which are stimulated once). (a) The response function R(θ, T_max) (open circles) and the fitting function R_fit(θ, T_max) (red line). (b) Time dependence of L for a single cell. (c) Time dependence of the average L for a population. (d) Time dependence of P for a single cell. (e) Time dependence of the average P for a population. (f) Time dependence of φ for a single cell. The two dashed red lines indicate the dynamics of φ for two other single cells. φ is very reproducible from pulse to pulse, even when φ ≠ 0. (g) Time dependence of the average φ for a population of 40 cells, which averages to zero. Error bars denote standard deviations.

In Fig. 3, we further quantify that the cell-to-cell versus pulse-to-pulse variability of R(θ, T_max). R(θ, T_max) is highly reproducible from pulse to pulse when a single cell is stimulated with 10 identical pulses of cAMP (Fig. 3a). In contrast, R(θ, T_max) for a population shows a large variability from cell to cell, although cells are stimulated with the same identical pulse (Fig. 3b), consistent with the data presented in Figs. 2 b–g.

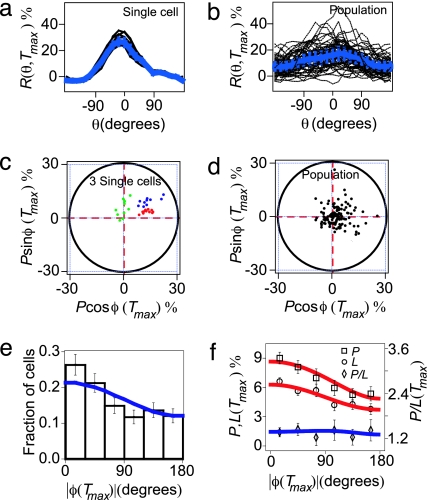
Fig. 3.

Comparison between single cell and population response. (a and b) R(θ, T_max) for a single cell that is stimulated 10 times (a) and a population of 40 cells that are stimulated once (b). (c and d) Polar plot of the polarization at T_max for three single cells (c) and a population of 100 cells (d). In these representations, one data point represents data from a single cell at T_max. The distance from a data point to the origin of the polar plot equals the polarization, P(T_max). The angle between the x axis and the line that connects the data point to the origin of the polar plot is the polarization angle, φ(T_max). (e) Population probability distribution of |φ(T_max)|, illustrating the fraction of cells displaying a particular polarization angle at T_max. (f) Average of L(T_max) and P(T_max) (left ordinate) and the ratio of P(T_max)/L(T_max) (right ordinate) as a function of |φ(T_max)|. (e and f) Solid lines are predictions of the geometric model.

In Fig. 3 c and d, we present P and φ in a polar plot (Supporting Text). For a single cell, φ is observed not to vary significantly from pulse to pulse (red dots in Fig. 3c), even when φ ≈ 90^o (green dots in Fig. 3c). In contrast, a pronounced cell-to-cell variability of the polarization angle φ is observed in the population, although the cells are stimulated with the same pulse of cAMP (Fig. 3d). The distribution of |φ(T_max)| is plotted in Fig. 3e, and shows a peak near φ ≈ 0. The same angular distribution is obtained over a wide concentration range of caged cAMP, which excludes the possibility that the variability is introduced at the level of the cAMP-receptor binding (19–21) (Supporting Text; see also Fig. 7, which is published as supporting information on the PNAS web site). These experiments demonstrate that, although there is a significant variability in φ(T_max) from cell to cell, the population faithfully detects the direction of the cAMP pulse. In contrast, the distribution of |φ(T_max)| for uniformly stimulated cells is flat (Fig. 8a, which is published as supporting information on the PNAS web site).

We find that both the localization and polarization show a strong correlation with the polarization angle as displayed in Fig. 3f. Cells that correctly detect the direction of the pulse (φ ≈ 0) have, on average, a 2-fold larger localization and polarization than cells that polarize in the opposite direction (φ ≈ 180^o). We will explain this correlation after we introduce the model. This correlation is absent when cells are stimulated with a uniform cAMP pulse (Fig. 8 b and c). The ratio of polarization and localization P/L does not show a significant correlation with the polarization angle (Fig. 3f).

A few stochastic models have been developed to describe random cell motility (22, 23); however, existing models of eukaryotic directional sensing are commonly constructed from spatially symmetric and deterministic systems of partial differential equations (24–30). Although the existence of an extracellular gradient can break the symmetry, the polarization by default will always occur along the direction of the extracellular gradient, yielding φ = 0 for all cells. Thus, for a cell to polarize in a direction other than the direction of the extracellular gradient, an additional source of symmetry breaking must be present in the cell’s gradient-sensing network.

Rather than modifying existing models designed to capture the full dynamics of directional sensing, we introduce a simple linear model that allows for symmetry breaking and focuses on cell-to-cell variability. To introduce a simple and general form of asymmetry, we assume that a cell has a static intracellular signal, S_int(θ). The intracellular signal might be caused, for example, by spatial inhomogeneities in any of the signaling molecules in the gradient-sensing pathway or might include an inhomogeneous distribution of cortical factors that remain bound to the membrane after actin depolymerization. It is unlikely that the symmetry is broken by an inhomogeneous distribution of cAMP receptors because the receptors are essentially uniformly distributed along the membrane (31). Our model accounts phenomenologically for this randomly oriented intracellular asymmetry without making statements regarding the molecular origins of the asymmetry.

This intracellular signal in general could be a very complicated function of the angle θ. Because we observe that polarization is well approximated by the lowest frequency cosine term, the lowest frequency components of the intracellular signal are also assumed to be the most dominant terms in producing polarization. Similarly, the extracellular signal in our experiment can be approximated by a single cosine function that describes how the extracellular cAMP concentration varies along the cell membrane.

The main assertion of the model is that the extracellular cAMP signal S_ext(θ) is combined multiplicatively with the intracellular signal S_int(θ) to produce an effective signal S_eff(θ). The following equations can be used to describe the geometric model:

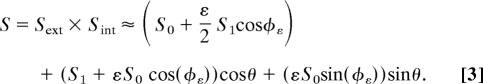In Eq. 1, we characterize the extracellular cAMP gradient around the cell periphery by an average concentration S₀ and an amplitude S₁. The coordinate θ defines the position along the membrane as defined in Fig. 1a. Similarly, in Eq. 2, the intracellular signal is characterized by a magnitude of the intracellular asymmetry ε and an angle φ_ε, which is the polar coordinate for which the intracellular signal is largest (Fig. 4d). The total signal S is a multiplicative function of the extracellular and the intracellular signals (Eq. 3) and can be approximated as

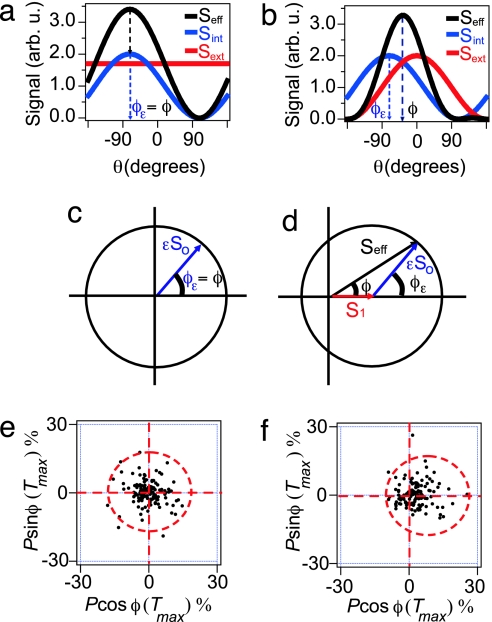
Fig. 4.

Schematic illustration of the geometric model. (a and b) The effective signal (black line), which is a combination of the intracellular signal (blue line) and the extracellular signal (red line), shown for a uniform cAMP stimulus (a) and for a directed pulse of cAMP (b). (c and d) Graphical representation of the geometric model and the polarization angle, φ, when cells are stimulated with a uniform pulse of cAMP and for a directed pulse of cAMP (d). The effective polarization angle strongly depends on the direction of the intracellular signal, φ_ε. (e and f) Experimentally measured polar plots, as defined in Fig. 3 c and d, for a uniform pulse of cAMP (e) and a directed pulse of cAMP (f).

When cells are stimulated with a uniform extracellular stimulation, the effective signal retains the direction of the intracellular signal and the direction of the effective polarization simply matches the direction of the intracellular signal φ_ε (Fig. 4a). Fig. 4b illustrates the case for which a cell is stimulated with a directed pulse of cAMP. In this case, an effective signal whose polarization is biased by the direction of an intracellular asymmetry causes a cell to polarize in a direction different from either the intracellular or extracellular signal.

Eqs. 6–8 can be geometrically represented in a polar plot when P_x and P_y are used as the x and y coordinates of the polar plot, respectively (Fig. 4 c and d). The polarization vector of the cell (Fig. 4d, black arrow) is proportional to the sum of a vector with length S₁ (Fig. 4d, red arrow) and a vector with length εS_o and angle φ_ε (Fig. 4d, blue arrow). The extracellular cAMP signal is parameterized by S_ext(θ) = S₀ + S₁cosθ, and the intracellular signal is parameterized by S_int(θ) = 1 + εcos(θ − φ_ε), where the parameters S₀ and S₁ reflect the average cAMP concentration and cAMP gradient, respectively. The parameters φ_ε and ε define the orientation and relative strength of the intracellular signal, respectively. This model predicts that for a uniform stimulation (S₁ = 0), the polarization angle φ equals φ_ε (Fig. 4c). Experimentally we find that when a population is exposed to a uniform stimulation the polarization angles φ are uniformly distributed from cell to cell (Figs. 4e and 8a), which implies that the orientation of the intracellular signal φ_ε follows the same distribution. For a directed pulse (S₁ ≠ 0) φ generally not does equal φ_ε. In this case, one would expect a nonuniform φ distribution with a maximum at θ = 0 as was experimentally observed (Figs. 3e and 4f). These results demonstrate that not only the direction of the intracellular asymmetry φ_ε but also the magnitude ε varies from cell to cell.

The model also qualitatively explains the experimental correlation between the polarization P and polarization angle φ (Fig. 3f). Because φ_ε is uniformly distributed (Fig. 4e), the strongest polarization is expected for cells in which the intracellular and extracellular signal line up (Fig. 4d, φ_ε = 0). In contrast, for cells in which the intracellular and extracellular signal are oriented in opposite directions (φ_ε = 180^o), the polarization P is expected to be the smallest possible. A similar argument can be made to explain the correlation between localization L and polarization angle φ. Eq. 5 of the geometric model predicts that the localization L is the strongest when the intracellular and extracellular signals line up (φ_ε = 0) and smallest when the intracellular and extracellular signals are oriented in opposite directions (φ_ε = 180^o).

Each data point in Fig. 4e (up to a constant S₀) contains the information about the magnitude and the direction of the intracellular signal for each cell. The mean of the εS₀ distribution for a population of 137 cells is 6.3 ± 0.4 with a standard deviation of 4.4 ± 0.3, leading to a coefficient of variation of 0.70 ± 0.04, which indicates that the strength of the intracellular signal is highly variable from cell to cell (Supporting Text; see also Fig. 9, which is published as supporting information on the PNAS web site).

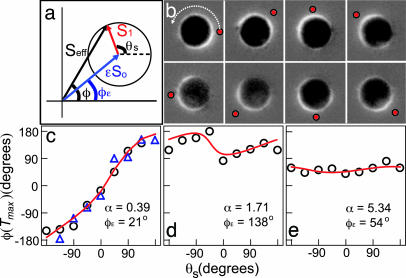
To test the model more directly, we stimulated a single cell from multiple directions. We varied the stimulation angle, θ_s, such that a cell was stimulated from eight different locations separated by 45^o while the orientation of the cell and the direction of the intracellular signal remain fixed (Fig. 10, which is published as supporting information on the PNAS web site). Fig. 5a schematically illustrates the geometric model in the frame of reference of a single cell, where the angle of the intracellular signal is fixed at φ_ε and the angle of the extracellular signal θ_s is rotated around the cell.

Fig. 5.

Experimentally measured relation between the polarization angle, φ(T_max), and the extracellular signal, θ_s, when the direction of the extracellular signal is varied relative to the intracellular signal, φ_ε and comparison to the geometric model. (a) Schematic illustration of the geometric model in the frame of reference of a cell with a fixed φ_ε. (b) The difference image for a cell with a small α (≪1). Red dots on the images indicate the direction of extracellular stimulation. (c) φ(T_max) versus θ_s for a cell with small α (≪1). The triangles and circles denote two independent experiments, demonstrating the reproducibility of this assay. (d and e) φ(T_max) versus θ_s for a cell with an intermediate α (≈1) (d) and a large α (≫1) (e). The red lines represent fits to the geometric model with fitting parameters α and φ_ε.

For a cell with small ε (≪S₁/S₀), we expect the contribution of the intracellular signal to the effective signal to be minimal, causing the effective signal to follow the extracellular signal exactly (φ ≈ θ_s, Fig. 5 b and c). In contrast, for a cell with large ε (≫S₁/S₀), the contribution of the extracellular signal to the effective signal is minimal; therefore, the effective signal will be predominately in the direction of the intracellular signal (φ ≈ φ_ε, Fig. 5e). For a cell with ε ≈ S₁/S₀, the intracellular and extracellular signals have equal strengths, which results in an effective signal that is neither in the direction of the intracellular signal nor in the direction of the extracellular signal (Fig. 5d). The fits to the geometric model using the two parameters α = εS₀/S₁ and φ_ε are in good agreement with our experiments (Fig. 5 c–e, red lines; see also Supporting Text).

To further challenge the predictive power of the geometric model, we tested whether the model combined with the single cell data in Fig. 5 could predict the population experiments summarized in Fig. 3 e and f. We experimentally found α for 20 cells (using the method outlined in Fig. 5), which had an average value of α = 3.6. Using this experimental value for α, the model successfully predicted the φ distribution and the ratio P/L without any fit parameters (Fig. 3 e and f, blue lines; see also Supporting Text). To predict how L and P vary with φ (Fig. 3f), we required one undetermined proportionality constant reflecting the ratio between the cAMP concentration and the experimentally measured response function R(θ). When this factor is used as the sole fit parameter, the experimental data closely match the model predictions (Fig. 3f, red lines). It is encouraging that this simple linear model correctly captures the key properties of the observed stochasticity in directional sensing.

Our results show that cellular asymmetries and cell-to-cell variability in the size of these asymmetries can have a significant impact on the fidelity of directional sensing. Whereas some individual cells correctly detect the extracellular cue, most cells display a significant deviation from this direction due to an intracellular asymmetry. However, this variability does not hinder a population of many cells from accurately detecting the direction of the extracellular cue (Fig. 3e). The model suggests that the effective signal is the product of a randomly oriented intracellular signal and the extracellular cue. Individual cells that, by chance, have the intracellular signal aligned with the extracellular cue will have a large effective signal and will therefore display a larger polarization than cells in which the intracellular and extracellular signal are counteracting. This mechanism biases the net polarization of the population toward the extracellular cue and furnishes a heterogeneous population with a simple, yet effective, response strategy that provides an isotropically sensitive direction sensor, even in the presence of large cell-to-cell variability.

Materials and Methods

Materials.

Adenosine 3′,5′-cyclic monophosphate, p1-(2-nitrophenyl)ethyl ester (NPE-caged cAMP; Calbiochem–Novabiochem, San Diego, CA) (32, 33) was used to create a controlled release and measurable gradient of cAMP. Fluorescein bis-(5-carboxymethoxy-2-nitrobenzyl) ether/dipotassium salt (Molecular Probes, Eugene, OR) was used to verify the two-dimensional diffusion calculations and visualize the gradient. Latrunculin A (Molecular Probes) was used to depolymerize actin.

Cell Culture.

A D. discoideum cell line expressing the CRAC–GFP was constructed by electroporating plasmid pWF1 [a generous gift from C. Parent (National Institutes of Health, Bethesda, MD)] into wild-type AX3 cells. CRAC–GFP cells were cultured and selected in HL5 medium with 20 μg/ml G418 and grown a density of 5 × 10⁶ cells per milliliter. Dictyostelium cells harvested by centrifugation were suspended in development buffer (DB; 10 mM phosphate buffer/2 mM MgSO₄/0.2 mM CaCl₂, pH 6.5). Cells were starved for 5 h in DB by repeated pulses of 75 nM cAMP every 6 min (12). Subsequently, starved cells were harvested and diluted 10³-fold in DB to reach the density of 10³ cells per milliliter and treated with 0.5 μM latrunculin A 10 min before observation. Cells were then seeded into the observation chamber, a round well with an inner diameter of 20 mm and a 1-mm depth adhered to a microscope slide (FW20 well; Grace Bio-Labs, Bend, OR). The observation chamber was covered with a coverslip and mounted on an inverted Nikon TE2000 microscope.

Data Analysis.

In our image analysis, we treat the cells as quasi-two-dimensional objects. Three-dimensional deconvolution analysis demonstrated that latrunculin-treated cells resemble spread-out droplets, with a maximum height of about one-fourth of the cell’s diameter. The diameter of a typical cell is ≈10 μm; therefore, the height is ≈2.5 μm. Cell were imaged with a ×60 objective with a depth of field of ≈1 μm. Therefore, a small contribution of the variability in the magnitude of the intracellular signal may be due to the out-of-focus fluorescence. Cells and their edges were determined with a nearest-neighbor-cluster-finding algorithm on autothresholded images. Abnormally shaped cells or cells that were touching were discarded for analysis. All curve fittings are done with the least squares method using MATLAB.

Abbreviation

CRAC

cytosolic regulator of adenylyl cyclase.