Repression and loss of gene expression outpaces activation and gain in recently duplicated fly genes

Abstract

Evolutionists widely acknowledge that regulatory genetic changes are of paramount importance for morphological and genomic evolution. Nevertheless, mechanistic complexity and a paucity of data from nonmodel organisms have prevented testing and quantifying universal hypotheses about the macroevolution of gene regulatory mechanisms. Here, we use a phylogenetic approach to provide a quantitative demonstration of a previously hypothesized trend, whereby the evolutionary rate of repression or loss of gene expression regions is significantly higher than the rate of activation or gain. Such a trend is expected based on case studies in regulatory evolution and under models of molecular evolution where duplicated genes lose duplicated expression patterns in a complementary fashion. The trend is important because repression of gene expression is a hypothesized mechanism for the origin of evolutionarily novel morphologies through specialization.

Many evolutionists argue that regulatory genetic changes may be more important in morphological evolution than changes in protein coding regions of genes (1–4). For example, some species with similar genomes have highly divergent phenotypes, suggesting regulatory differences (5), and many simple regulatory mutations are known to have drastic morphological effects (4, 6). Furthermore, in evolving genomes, change in gene expression is an important mechanism for the retention of duplicate genes (7, 8). Namely, most duplicate genes are expected to be lost from the genome, unless one gene gains a new function or the duplicates partition the ancestral function. Despite this importance, few broad generalities have been demonstrated regarding the macroevolution of gene regulation.

Two lines of evidence from different research programs suggest a general, but largely untested, hypothesis regarding gene regulatory evolution: Loss of gene expression is faster during evolution than gain. First, the evolutionary diversification of repeated morphological structures often involves differential repression of gene regulatory networks in one or more of the replicated structures. For example, the developmental pathway leading to limb formation is repressed in insect abdomens compared with ancestors that probably possessed abdominal limbs (9, 10). Additionally, in fly halteres (which are balancing organs evolutionarily derived from wings), the protein Ubx represses the expression of genes involved in wing growth and flattening (11, 12). Second, molecular evolutionists have proposed the duplication-degeneration-complementation (DDC) model of gene subfunctionalization, which requires multiple losses of gene expression regions (7, 13). Under DDC, genetic regulatory elements are duplicated during gene duplication events. Subsequently, mutations increase specialization of gene function by degenerating modular regulatory elements in a complementary fashion in the duplicated genes, a process that may be involved in the duplicated genes’ long-term preservation (7).

Here, we take a single-species approach to investigating patterns of the macroevolution of gene expression. Macroevolution (here defined as evolutionary patterns and processes involved in splitting lineages; in this case, gene lineages) may be investigated in a single species because the genome of any species has formed, in part, by ancient evolutionary events, such as gene duplications (14). By recognizing that gene expression is a trait of genes evolving in branching gene families, we can use phylogenetic methods to test general hypotheses by using single-species data (14, 15). Drosophila melanogaster is an outstanding organism to use for such a study because of exceptional genomic resources, including annotated spatial gene expression data from automated in situ hybridization experiments (16). We took advantage of these data by grouping D. melanogaster genes into families (Fig. 1) and analyzing the expression patterns of genes by using phylogenetic comparative methods (see Materials and Methods; see also Supporting Methods and Tables 1 and 2, which are published as supporting information on the PNAS web site). Briefly, we used coding sequence data to estimate gene family phylogenies in flies and scored discrete gene expression domains as characters of genes. Each gene expression domain has two possible character states for each gene: expressed or not expressed. We then assume a Markov model of trait evolution and use maximum likelihood to estimate two rate parameters: rate of gain and rate of loss of gene expression domains.

Fig. 1.

The two data types used in our analyses include gene family trees and gene expression patterns (black ticks). We first grouped genes into families and constructed gene trees based on coding sequence data by using maximum likelihood (ML) (see Materials and Methods for details). Next, we mapped expression patterns on to gene phylogenies assuming a binary Markov model and estimated parameters of the model with ML. We scored 115 expression domains from a published data set (16) as present or absent for each of 107 genes. These expression domains are depicted in 115 columns to the right of the gene family trees above. Black ticks indicate a particular gene (row) is expressed in a particular domain (column). Gene families are alternately shaded gray or white to indicate no expression in particular domains.

Our single-species approach has several advantages for studying gene expression evolution. First, ambiguities of expression homology across species are avoided. Second, by studying overall gene expression patterns, we integrate over all different mechanisms, including cis- and trans-acting mechanisms that produce patterns of mRNA expression in cells. We do not require detailed understanding of those mechanisms to test general evolutionary hypotheses. However, our analysis does not consider posttranslational regulation, which some regard as less important in evolution than transcriptional regulation (1). A third advantage is that the genomic data are abundant and chosen arbitrarily with respect to the hypothesis at hand. These attributes allowed us to conduct the first test of the general hypothesis that gene expression is more commonly lost than gained during the evolution of genes.

Results and Discussion

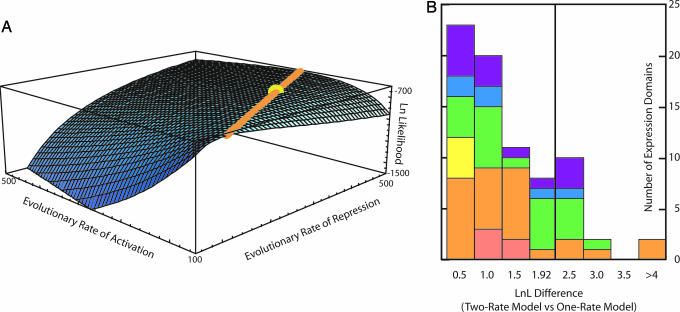
Our results significantly reject the null hypothesis that the rate of repression equals the rate of activation of gene expression regions. A two-rate model of evolution has a significantly higher likelihood (−717.06) than a one-rate model (−786.58) based on a standard likelihood ratio test (P < 0.0001). Furthermore, parameter estimates indicate that repression rate is at least twice that of activation in the fly gene families examined (Fig. 2A). These statistically significant results are based on simultaneously estimating the two model parameters across all fly gene families for which we had expression data. However, different gene families or different individual expression domains might have different rates of gain and loss of gene expression, potentially leading to spurious statistical results. We examined these possibilities by analyzing each gene family and each expression domain independently. We found that in 24 of 26 independent gene families, loss outpaced gain. This difference is statistically significant in a sign test (P < 0.0001) again rejecting the null hypothesis that rate of loss equals that of gain. Finally, we found that in 76 of 76 individual expression domains, estimated rates of loss were higher than gain (we could not obtain parameter estimates for all 115 domains because of insufficient data when analyzing certain individual domains). Fourteen individual domain analyses showed significant support for a two-rate over a one-rate model of evolution (Fig. 2B).

Fig. 2.

Maximum likelihood analyses of gene expression evolution. (A) Likelihood surface for the evolution of fly gene expression domains. Blue surface (z axis) represents log likelihood values for varying rates of activation (x axis) and repression (y axis) in arbitrary units. The yellow sphere indicates the parameter value that maximizes the likelihood function (repression rate = 340.712, activation rate = 161.344, and ratio = 2.11). The orange line represents parameter values statistically indistinguishable from the maximum; the ratio of activation to repression rate on the orange line is a constant 2.11. Any point on the line, including the yellow maximum, is highly significantly different from a line with ratio 1.0. These results firmly reject a null hypothesis that activation rate equals repression rate and indicate that for the data at hand, repression is twice as fast as activation during evolution. Because the orange line is not statistically different from the maximum, we cannot confidently infer the absolute rate of domain activation and loss. (B) Statistical analyses of individual expression domains. The statistic (x axis value) is the difference between the log likelihood of a two-rate and one-rate model. Values >1.92 show statistically significant support for the two-rate model based on a standard likelihood ratio test by using a χ² distribution. Different colors indicate which system/tissue type the domains are expressed: Pink, circulatory; orange, digestive; yellow, muscle; green, nervous; blue, tracheal; purple, other. See Supporting Methods for all individual tests.

Another consideration is the potential nonindependence of regulatory mechanisms: Single mutational events could delete multiple expression regions by altering trans regulation of multiple genes or deleting multiple cis-regulatory regions of a single gene. Our results do not support this idea because the individual expression domains that contribute most extensively to the bias are expressed in multiple different tissues/systems, like digestive, nervous, and other systems (Fig. 2B). In any event, we argue that potential nonindependence is not a concern because we are considering the pattern of gene region loss and gain. No matter the mechanism, simultaneous multiple loss or single independent losses, the pattern of loss outpacing gain is statistically validated in our tests.

How much of the observed bias toward loss of expression regions results from the partitioning of ancestral gene expression patterns by DDC? To address this question, we used our statistical approach to estimate the likelihood that different classes of evolutionary histories produced the observed gene expression patterns. We noted that DDC subfunctionalization yields a specific pattern of expression region evolution, whereas an ancestral gene possesses the additive gene expression complement of duplicated descendent genes. Therefore, DDC is consistent with only a portion of possible ancestral histories of gene expression. Similarly, other ancestral histories are consistent only with other modes of gene expression evolution besides DDC (Fig. 3).

Fig. 3.

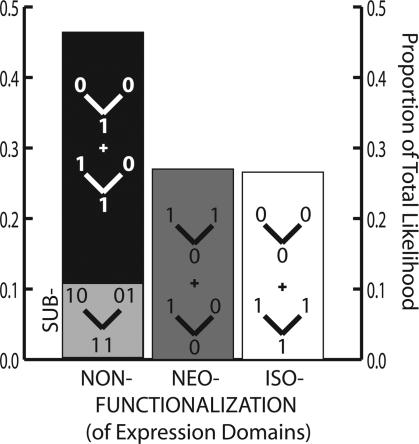
We examined the likelihood that observed patterns of gene expression were generated by three different processes, non-, neo-, or iso-functionalization of gene expression domains. We considered every node in every three-gene phylogeny and every expression domain of Fig. 1 and summed likelihood values over all possible ancestral states. Consistent with Fig. 2A, nonfunctionalization (repression) is likely to account for more of the observed patterns than neofunctionalization (activation). A subset of the likelihood attributable to domain nonfunctionalization (note we refer here to loss of expression, not loss of an entire gene, as usually implied by the term nonfunctionalization) is consistent with a mechanism of complementary repression (subfunctionalization), leading to specialization of ancestral gene function.

As such, we were able to partition all possible evolutionary histories into those consistent with four evolutionary processes: (i) DDC subfunctionalization, (ii) noncomplementary loss of gene expression in one or both duplicated descendent genes, (iii) gain of gene expression in one or both duplicate genes (neofunctionalization; ref. 7), and (iv) no change in expression from ancestor to duplicated descendent genes, (which we here term “iso-functionalization”). Because we do not know the ancestral states of expression before gene duplications occurred, we analyzed all possible evolutionary histories, summing likelihood values over gene families and expression regions for each of the four process categories (Fig. 3).

Results of these analyses illustrate a signal consistent with DDC subfunctionalization but also indicate that other processes, especially noncomplementary loss, are probably more important drivers of the total observed gene expression patterns in duplicated fly genes. These results indicate that a mixture of evolutionary mechanisms probably contributed to observed expression patterns in fly gene families. Although many gene expression regions were gained or unchanged after gene duplication events, the loss of expression regions, some by subfunctionalization, has been the primary driver of observed expression patterns in fly gene families. These results may be affected by our examination of a single stage of fly development. For example, subfunctionalization frequency may increase when examining other stages. However, gain and pure loss of expression regions also might increase when looking at more stages. Because we know of no a priori reason to believe that examining one stage should systematically bias our results, we argue they are robust in this regard.

Overall, our results raise an important question: If gene expression regions are more commonly lost than gained, why is all gene expression not eventually lost over evolutionary time? One answer is that expression regions of duplicated genes may share common ancestry, for example by the duplication of a modular cis-regulatory element concomitant with gene duplication. Note that duplication of cis-regulatory elements is an explicit part of the DDC model of gene duplicate retention described above. As such, two duplicate genes expressed in the same region share a single, ancestral evolutionary origin of activation, yet the duplication event allows for two separate repression events during later evolution. This logic can be formalized as a duplication-birth-death (DBD) model (see Supporting Methods), where we model rates of gene duplication and expression domain birth and death. The DBD model confirms the potential for long-term maintenance of discrete gene expression regions, even when assuming that domain loss is twice as common as domain gain during evolution. In addition, the DBD model suggests the potential for a correlation between the rate of gene duplication and rate of loss of expression domains; under equilibrium conditions, more rapidly duplicating families should show more rapid rates of expression loss, a hypothesis that deserves empirical testing. Coupled with the DBD model, our results highlight the fact that because genes and their expression domains duplicate commonly, they must also be lost commonly. As such, the patterns of loss may be as important as gain in dictating the evolution of genomes and phenotypes.

How general are our results that loss of expression domains outpaces gain? The current results are based on the only genomic data available with a highly consistent and complete annotation of spatial gene expression. Although it is a large data set chosen arbitrarily with respect to the hypothesis at hand, the possibility of bias in the data still exists. We examined this possibility by investigating gene ontology (GO) annotations for the genes analyzed (Table 3, which is published as supporting information on the PNAS web site). Many analyzed genes are involved in physiological processes; also many are involved in “establishment of localization.” Notably, some important classes of genes were not present in our analysis such as transcription factors. Reasons may be that transcription factors duplicate rather infrequently and may contain gene regions that evolve quickly. As such, they usually would not meet the stringent criteria for gene family membership that we used.

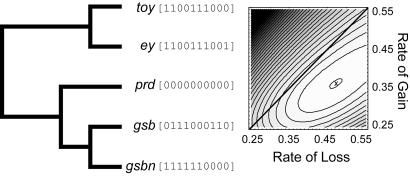
Because of the absence of transcription factors from our analyses, we analyzed a family of D. melanogaster transcription factors, containing “paired” domains. This family has been characterized for expression and is known to possess related genes (17, 18). We found maximum likelihood estimates of parameter values to show a ratio of loss to gain as 1.3, consistent with our estimates from other genes (Fig. 4). Not unexpectedly, a two-rate model did not fit the data significantly better than a one-rate model: The statistical power available with only five genes is very low. Mooers and Schluter(19) suggested that even analyses with on average 21 tips often did not have enough statistical power to prefer two-rate models. With respect to transcription factors, we conclude that the trend toward faster loss is upheld in our analysis of fly paired genes, but that a definitive answer awaits more comprehensive data and analyses. We hypothesize that the result of faster loss of expression should generalize to most gene families, including transcription factor genes, but as discussed above, may be affected by rate of gene duplication. More rarely duplicated genes, including transcription factor families, might a show lower ratio of rate of expression domain loss to gain compared with more rapidly duplicating gene families, as suggested by our equilibrium DBD model.

Fig. 4.

Expression rate analysis of paired-containing genes from D. melanogaster. (A) Bayesian consensus phylogeny of five genes. Expression data are in brackets, columns represent expression in lateral cord, ventral nerve cord, anal pad, hypopharynx, central brain, CNS, optic lobe, mesoderm, labral segment, and Bolwig’s organ. 0 = not expressed, 1 = expressed. (B) Likelihood surface for the evolution of expression of paired gene family. Log likelihood of one-rate model is −33.81, and two-rate model is −33.57. Based on a two rate model, the estimated ratio of loss/gain is 1.3 (0.47/0.36).

In summary, an emerging theme in evolutionary genomics is that loss is a major factor in evolution (20). For example, gene duplication is quite common, and the fate of most duplicated genes is loss (21). At least in several cases, DNA loss may be related to a mutational bias, where deletion mutations outnumber insertion mutations (22–24). Here we present strong statistical support for a similar loss hypothesis for the evolution of discrete regions of gene expression. Our data were chosen without respect to the hypothesis at hand but represents rapidly duplicating genes, which may have higher rates of expression domain loss. Nevertheless, the methods introduced here are general and could be used to test the hypothesis in future studies by using more data from any species or multiple species. Our results support the idea that gene duplication and loss of discrete, modular expression regions may provide a general mechanism for increased specialization over evolutionary time that may be linked with increases in genomic complexity by gene duplication.

Materials and Methods

We used fly functional genomic data including gene sequences and published expression patterns of those genes (16). We performed a gene ontology analysis by using DAVID (25). Next, we grouped fly genes into families by following methods described in refs. 15 and 26 and estimated separately the phylogenetic relationships of genes in each family by using standard phylogenetic methodology (see also Supporting Methods). We considered expression patterns to be traits of genes that have evolved during the history of gene families, allowing us to compare expression to gene family phylogenies estimated separately from coding sequence data (ref. 15; Fig. 1). Expression patterns were divided into discrete expression regions (we usually use the term expression domain, which should not be confused with protein domains), including CNS, gut, and eye (see Supporting Methods), resulting in 115 separate regions. Each gene was scored as either “expressed = 1” or “not expressed = 0” for every discrete expression region. We next considered each region to be a character of a gene and used a standard binary Markov model to compare expression data to gene trees (27–29).

The two-state Markov model has two parameters, rate of repression/loss and rate of activation/gain (our analysis does not distinguish between repression or loss of a modular cis-regulatory element). We used maximum likelihood to estimate the parameters and compare the rates of repression to activation. The methods sum over all possible ancestral states and do not rely on explicit reconstruction of evolutionary history (27, 28).

Data.

We obtained in situ hybridization data from the Berkeley Drosophila Genome Project (BDGP) and stored all data in a local MySQL database. Amy Beaton of BDGP performed annotation of in situ experiments, consisting of >56,000 photos documenting expression of 3,012 genes. For our study, we used data from fly embryonic stages 13–16, the stages with the most data.

Trait Mapping.

The probabilities (P) of changing from one state (expressed) to another (not expressed) over time are functions of the rates of gain + activation (a) and loss + repression (β) and are related by the equation P(t + 1) = P(t) × Qt, where Q is the instantaneous rate matrix, and t denotes time. Branch lengths of the phylogenetic gene trees were used as a proxy for time (t). Different branch length assumptions, such as treating all branches as equal, did not qualitatively change our conclusion of biased evolutionary rates. To obtain parameter estimates, we maximized the likelihood function by using Mathematica (Wolfram) across all gene families and expression regions. For the values reported, we included only expression regions within each gene family in which one of these genes actually is expressed. This approach is conservative with respect to our hypothesis, because adding partial likelihood functions where all genes in a family are in state 0 (not expressed) would bias the result toward a higher rate of repression (30, 31).

Paired Family Analysis.

We obtained five paired family protein sequences from GenBank and estimated a phylogeny by using only the paired domain protein sequences. We assumed the protein mixed model in MrBayes and used the consensus tree for character analysis. We scored 10 expression characters and performed trait mapping as described above (see Fig. 4 for additional details).

Supporting Information.

Additional results can be found in Figs. 5–7, which are published as supporting information on the PNAS web site.

Abbreviation

DDC

duplication-degeneration-complementation