Abstract
A large number of experimental studies have been devoted to quantifying the interaction between transmembrane (TM) helices in detergent micelles and, more recently, in bilayers. Theoretical calculation of association free energy of TM helices would be useful for predicting the propensity of given sequences to oligomerize and for understanding the difference between association in micelles and in bilayers. In this article, the theoretical foundation for calculating the standard association free energy of TM helices is laid out and is applied to glycophorin A in both micelles and bilayers. The standard association free energy is decomposed into the effective energy, translational, rotational, and conformational entropy terms. The effective energy of association is obtained by molecular dynamics simulations in an implicit membrane model. The translational and rotational entropy of association is calculated from the probability distribution of the translational and rotational degrees of freedom obtained from the molecular dynamics simulations. The side-chain conformational entropy of association is estimated from the probability distribution obtained by rigid rotation of all side-chain dihedral angles. The calculated standard association free energy of glycophorin A in N-dodecylphosphocholine micelles is in good agreement with the experimental value. The translational entropy cost is larger, whereas the rotational entropy cost is smaller in bilayers than in micelles. The standard association free energy in 1,2-dimyristoyl-sn-glycero-3-phosphocholine bilayers is calculated to be ∼1.3 kcal/mol more favorable than in N-dodecylphosphocholine micelles, consistent with available experimental data.
INTRODUCTION
Association of transmembrane (TM) helices is a fundamental process in membrane protein structural biology. The helices may belong to multiple-span membrane proteins, in which case their association leads to tertiary structure formation (1); or they may belong to single-span membrane proteins and their association can play an important functional role. The oligomerization of membrane receptor proteins is thought to be very important for signal transduction; however, the extent to which the TM domain contributes to this oligomerization is still unclear or even controversial (2). Association of TM helices can be experimentally determined by analytical ultracentrifugation and fluorescence resonance energy transfer (FRET) in vitro (3–7) or by ToxR/ToxCat in vivo (8–10). From the theoretical point of view, it would be useful to be able to predict a), to what extent two given TM helices will associate, and b), the structure of the dimer or oligomer. This article deals with the first problem: given the structure of a TM helix dimer, predict the association free energy in bilayers and in micelles.
Glycophorin A (GpA), a small bitopic (single-span) TM protein found in erythrocyte membranes, has been studied extensively as a model system for the association of TM helices. Mutagenesis analyses showed that homodimerization of GpA during SDS-PAGE is highly dependent on sequence specific interhelical interactions (11,12). The seven amino acid motif LIxxGVxxGVxxT was found to be essential for association of GpA based on these studies (13). Similar results were obtained in membrane bilayers in vivo (8). These conclusions were confirmed by the determination of the structure of the GpA dimer in micelles (14) and in bilayers (15). The association free energies of wild-type GpA and GpA mutants in a number of micelle environments have been determined experimentally: in C8E5 micelles by analytical ultracentrifugation (3,4); in a series of detergents with different alkyl chain length and headgroups by FRET (6,7); and in C14 betaine micelles by analytical ultracentrifugation (5). However, the association free energy of GpA in lipid bilayers is not available.
The relationship between association free energies determined in micelles and bilayers is not well understood (16). Langosch et al. (10) have shown that GpA TM segments appear to be less sensitive to mutation and thus more strongly associated in a natural lipid bilayer than in micelles, probably due to a slightly altered structure of the dimer and/or to a higher local concentration and preorientation of the TM helices in a lipid bilayer. Furthermore, it was found that the association of TM helices of the M2 protein from influenza A virus is two orders of magnitude stronger in 1,2-dilauroyl-sn-glycero-3-phosphocholine bilayers than in detergent N-dodecylphosphocholine (DPC) micelles and even stronger in 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC) and 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine bilayers (17). The origin of this difference is unknown. Considering that M2 forms a tetrameric structure with four predicted helix-helix association interfaces (18), the difference in association constant corresponds to ∼0.7 kcal/mol for each helix-helix interface.
Although protein-protein and protein-ligand binding free energy in aqueous solution have been extensively studied (19–24), little work has been done on the theoretical prediction of association free energy of TM helices. Due to the inhomogeneity along the membrane normal, binding free energy calculations in a membrane should be different from those in aqueous solution. Recently, an empirical method has been proposed to estimate association free energies of α-helices in nonpolar media (25). However this method has several limitations: 1), it neglects the translational and rotational entropy changes upon association; 2), it does not address the difference between micelles and bilayers; and 3), possible conformational changes in the helices upon association are not accounted for. More recently, Henin et al. (26) estimated the free energy change along a reaction coordinate for GpA dimerization and free energy changes due to mutations, and obtained the association free energy by integrating the potential of mean force. Many other simulations of associating TM helices have been reported in micelles or bilayers (27–31) but have not included calculations of the association free energy.
In this article, a general method to calculate the association free energy of TM helices from molecular dynamics (MD) simulations is proposed based on an implicit membrane model (IMM1) (32). The method is applied to the calculation of the standard association free energy of GpA in both detergent micelles and membrane bilayers. The standard association free energy is decomposed into the effective energy, translational, rotational, and conformational entropy terms. The effective energy of association is obtained by MD simulations in IMM1. The translational and rotational entropy of association is calculated according to the probability distribution of three translational and three rotational degree of freedom obtained from the MD simulations. The side-chain conformational entropy of association is estimated from the probability distribution obtained by rigid rotation of all side-chain dihedral angles. The calculated standard association free energy of GpA in DPC micelles is in good agreement with the experimental value. The standard association free energy in DMPC bilayers is calculated to be ∼1.3 kcal/mol more favorable than in DPC micelles, consistent with available experimental data.
THEORY
Choice of standard state
Because the free energy of a bimolecular reaction depends on the concentration of the reactants, association free energies are reported at given concentrations (the standard state). The standard state is implied in the units used to define the equilibrium constant. For GpA, sedimentation (3–5) and FRET (6,7) data were used to obtain the relative amounts of dimer and monomer. The apparent association constant is defined as
 |
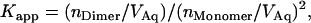(1) |
where nDimer and nMonomer are numbers of moles of dimer and monomer species, respectively, and VAq is the volume of the aqueous solution. The standard state implied in Eq. 1 is 1 M in bulk solution. The problem with apparent association constants is that they depend on the amount of detergent (4). To eliminate this problem, the mole fraction equilibrium constant, KX, was introduced, which is related to the apparent association constant by
 |
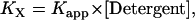(2) |
where [Detergent] is the molar concentration of detergent in the bulk solution. The mole fraction standard free energy of GpA upon association in C8E5 and C14 betaine was measured as −7.0 kcal/mol and −5.7 kcal/mol, respectively (4,5). The apparent dissociation constants of GpA in N-dodecyl-N,N-(dimethylammonio)butyrate and DPC detergent micelles were determined as 0.08 ± 0.04 μM and 0.16 ± 0.08 μM, respectively, at 25 mM detergent concentration (6), from which the mole fraction standard association free energy of GpA in N-dodecyl-N,N-(dimethylammonio)butyrate and DPC is calculated as −7.1 kcal/mol and −7.6 kcal/mol, respectively.
Because molarities lend themselves more naturally to theoretical calculations, we adopt 1 M as the standard state for our calculations, but it is defined only within the hydrophobic phase (HP), micelles, or bilayers, to eliminate the dependence of association constants on the amount of detergent or lipid. To convert the standard association free energy on the mole fraction scale to our own standard state, we start from the definition of association constants. KX is defined as (4)
 |
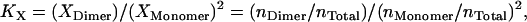(3) |
where Xi and ni are the mole fraction and number of moles for protein species i in the hydrophobic phase, respectively, and nTotal is the total number of moles of all protein species and detergent/lipid molecules in the hydrophobic phase. At dilute conditions, one can make the approximation that nTotal ≈ nDetergent, where nDetergent is the number of moles of detergents/lipids in the hydrophobic phase. Then
 |
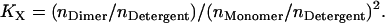(4) |
The molar association constant can be defined as
 |
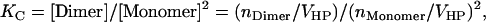(5) |
where [i] is the molar concentration of species i in the hydrophobic phase and VHP is the total volume of the hydrophobic phase including proteins and detergent/lipid molecules. A similar approximation that VHP ≈ VDetergent, where VDetergent is the volume of the detergent/lipid molecules in the hydrophobic phase, can be made if the proteins are dilute in the hydrophobic phase; then
 |
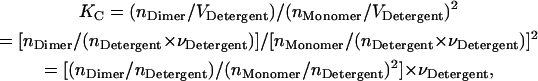(6) |
where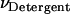 
is the molar volume of hydrophobic tails of pure detergents/lipids. Combining Eqs. 4 and 6, we obtain
 |
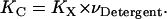(7) |
The standard association free energy at 1 M (in HP) standard state is
 |
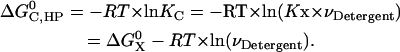(8) |
It was estimated that the molar volume of the −CH2-CH2− group is 32.2 cm3/mol (33), thus the molar volume of hydrophobic tails is ∼0.193 L/mol for DPC detergent micelles. Equation 8 then gives ∼−6.1 kcal/mol for the 1 M (in HP) standard association free energy of GpA in DPC micelles.
Since a membrane is a two-dimensional medium, the concentration of TM helices in a membrane bilayer would be more naturally expressed in units of mole/area. 1 mol/liter can be easily converted to mole/area if the thickness of hydrophobic core of membrane (T) is specified; 1 M (in HP) corresponds to 1660 Å3 per molecule. Therefore, the average area for each molecule is
 |
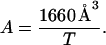(9) |
The surface concentration of TM helices (CONsurface, in units of mole/area) is
 |
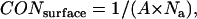(10) |
where Na is Avogadro's number. For example, if the thickness of hydrophobic core of membrane is 23 Å, the corresponding area for each molecule of each species in membrane is 72.2 Å2/molecule (note that this is similar to the area per lipid in common membranes); the surface concentration is 2.3 × 10−6 mole/m2. Although surface concentration is more natural for the two-dimensional membrane, the molar concentration is more frequently used in thermodynamics, so 1 molar standard state in hydrophobic phase is kept in our calculations.
Association in bilayers
Most previous theoretical calculations of association or binding free energy (19–24) were performed in bulk solution, which is isotropic in six dimensions (three rotational and three translational). However, in the IMM1 model, the x and y axes on the membrane plane are isotropic, whereas the z dimension is anisotropic. Among three rotational dimensions (three Euler angles) only one (about the z axis) is isotropic. Different formulas should be used to calculate the rotational and translational entropy lost on isotropic and anisotropic dimensions.
Since rotations and translations on the anisotropic dimensions are restricted to a relatively narrow range, we assume that an MD simulation (for example, 1 ns) is sufficient for sampling distribution functions for rotation and translation on the anisotropic dimensions. This assumption was validated by a series of 1 ns MD simulations of a GpA monomer that started from different initial positions on the z axis and different initial orientations about the y axis and helical axis, but obtained very similar distributions on these dimensions (data not shown). Therefore, the following basis is proposed for our entropy calculations:
Monomer and dimer translate and rotate freely on the isotropic dimensions and their translational and rotational entropy on these dimensions can be calculated analytically.
The entropy loss upon association on the isotropic dimensions is contributed by only one helix. Upon association, one helix still samples the available space specified by the standard state but the second helix has limited freedom to move relative to the other.
On the anisotropic dimensions, the entropy changes for each helix from free to bound state are calculated separately and added.
The translational and rotational entropy loss on the isotropic dimensions can be calculated based on the relative distances or relative Euler angles of one helix with respect to the other as described for the binding process in solution (21). For the entropic contribution from anisotropic dimensions, the calculation method should be modified.
As in the calculation of binding free energies in solution (21), the standard association free energy (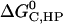
) can be decomposed into effective energy change (
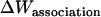), translational entropy loss (
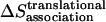), rotational entropy loss (
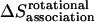), and conformational entropy loss (
):
 |
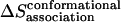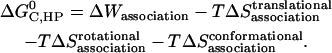(11) |
Calculations of these components are discussed in the following sections.
Effective energy change upon association
Effective energy change upon association (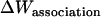
) is the average effective energy of the dimer (
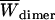) minus the average effective energy of the two monomers:
 |
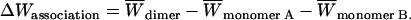(12) |
Another expression for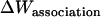 
can be derived from Eq. 12 (21):
 |
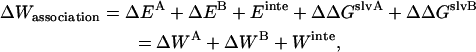(13) |
where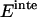 
is the interhelical interaction energy, 
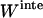is the interhelical effective interaction energy, 
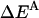and 
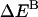are the changes in intramolecular energy, 
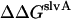and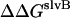 
are solvation free energy changes, and 
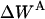and 
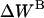are the reorganization energy of A and B, respectively (21). The difference between energies and effective energies is that the latter include solvation effects. That is, 
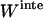is equal to 
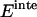plus the loss of solvation of each helix due to the other helix. 
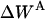is equal to 
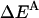plus the change in solvation of each atom in helix A due to other atoms in helix A.
Translational entropy loss upon association
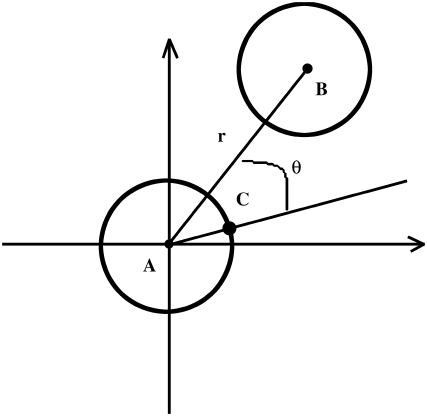
The translational entropy loss upon association (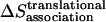
) in lipid bilayers is mostly due to restriction of motion on the plane of the membrane, i.e., isotropic dimensions x and y. For dimerization, it is more natural to use polar coordinates (r, θ), where r is the distance between the centers of the helices and θ is the angle between the vector connecting the centers of mass of the two helices and the vector from the center of reference helix to one of the Cα atoms on the reference helix (Fig. 1).
FIGURE 1.
Polar coordinate system on the x, y plane of the membrane. The two helices in a dimer are presented as two cylinders. Points A and B are the center of the reference helix A and the center of the moving helix B, respectively. Point C represents a specific Cα atom on the reference helix. r is the distance between points A and B, and θ is the angle between AB and AC.
Preliminary tests showed that the distributions of r and θ are highly coupled; therefore, in the calculations we use the coupled distribution of r and θ (Eq. 14). The loss of translational entropy on the membrane plane is due to: a), reduction in amplitude of r and θ,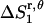 
; b), the uneven distribution of r and θ within the allowed range, 
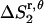; and c), the change of “communal entropy”, shown by the first, second, and third terms on the right-hand side of Eq. 14, respectively:
 |
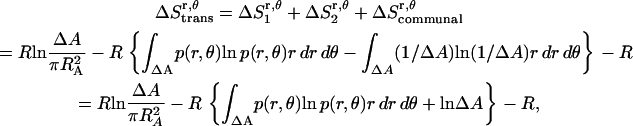(14) |
where R is the gas constant, p(r, θ) is the normalized probability distribution of r and θ (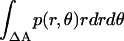
= 1), RA is the radius of the average area A for each monomer at 1 molar standard state (RA = 
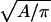), and ΔA is the surface area (ΔA= 
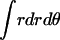) in which one helix is observed to move relative to the other helix. p(r, θ) = 1/ΔA corresponds to a flat distribution. The first and second terms in Eq. 14 are essentially from a “cell theory” approach; each molecule is allowed to move within a “cell”, the size of which is determined by the standard state. It neglects the possibility of multiple occupancy of the cells. The latter contributes a term referred to as “communal entropy” and is equal to R (34). When 2 mol of monomers form one mole of dimer, this term contributes –R to the translational entropy loss upon association. This term was incorrectly omitted in previous work in bulk solution (21).
Translational entropy loss upon association in lipid bilayers may also occur along the z axis, an anisotropic dimension. Preliminary tests also showed coupling of absolute z coordinates of the two helices; therefore, the joint distribution was used to calculate the translational entropy lost on the z axis. The translational entropy change upon association on the z axis is the difference in translational entropy of two coupled helices after association and translational entropy of two independent monomers on z axis,
 |
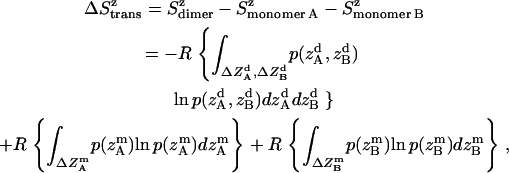(15) |
where all probability distributions are normalized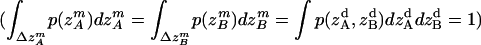 
; A and B represent helices A and B; d and m denote the helix in a dimer or as a monomer, respectively. In Eq. 15) 
, 
, 
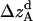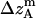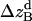, and 
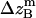are the amplitudes of 
, 
, 
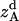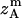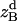, and 
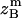, respectively, obtained from MD simulations; 
, 
, 
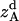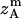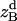, and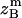 
, are absolute z coordinates of helix A in a dimer; helix A as a monomer; helix B in a dimer; and helix B as a monomer, respectively. For a homodimer, the last two terms are identical.
The total translational entropy loss upon association in bilayers is
 |
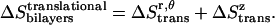(16) |
Rotational entropy loss upon association
Any orientation of a rod-like TM helix can be defined by a unique combination of three Euler angles. In this work, we define the three angles as follows. Starting from a reference where the helix lies along the x axis (see caption of Fig. 2), any orientation can be obtained by a three-step operation (shown in Fig. 2): a), rotate about the x axis (the helical axis) by an angle α (i.e., α is the rotation angle); b), rotate about the y axis by an angle 90° − β (i.e., β is the tilt angle); and c), rotate about the z axis by an angle γ. Thus, to determine the Euler angles of any given orientation of a helix during MD simulations, one needs to find the reverse operations to return the orientation back to the reference state.
FIGURE 2.
Three Euler angles (A) and the reference state (B) in the rotational entropy calculations. The reference state is defined as follows: a), the center of 21 α-carbon atoms on residues from Thr-74 to Gly-94 (from CA 5 to 25) is at the origin (0, 0, 0); b), the center of seven α-carbon atoms on residues from Thr-74 to Val-80 (from CA 5 to 11) is on the +x axis; and c), the α-carbon atom on residue Val-84 (CA 15) is on the x, y plane and its coordinate on the positive y axis.
In aqueous solution, it was assumed that the probability distributions of all three Euler angles are independent (i.e., p(α, β, γ) = p(α)p(β)p(γ)) (21). This assumption is likely to fail in membranes; for example, for β = 0, all α-angles are equally probable, but for β ≠ 0 they are not. Indeed, preliminary tests showed that the distributions of α and β of a helix are coupled with each other. Thus in the membrane it can be assumed that p(α, β, γ) = p(α, β)·pγ for a monomer (pγ is constant since γ is isotropic). The dimer can rotate isotropically around the z axis. We can think of one helix maintaining its full freedom in the γ-angle, but the γ-angle of the second helix is now correlated with that of the first helix. The dimer is then described approximately by the probability distribution
 |
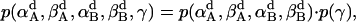(17) |
where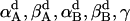 
are the rotational angles of each helix in a dimer from the reference state and γ = γB − γA. Therefore the rotational entropy change is decomposed into two contributions: one from the γ-angle and the other from the α- and β-angles.
Rotational entropy loss in bilayers from the γ-angle is given by
 |
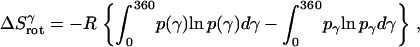(18) |
where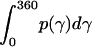 
= 1, and 
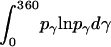is the rotational entropy corresponding to free rotation of a monomer (
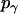is a constant value determined from normalization 
.
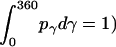Rotational entropy loss in bilayers from angles α and β, anisotropic dimensions, occurs for both helices, shown by Eqs. 19–22:
 |
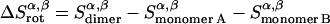(19) |
 |
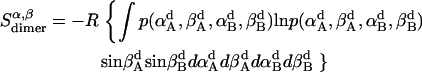(20) |
 |
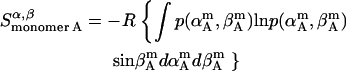(21) |
 |
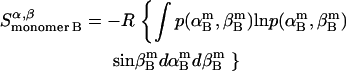(22) |
The total rotational entropy loss upon association (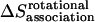
) in lipid bilayers is
 |
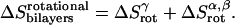(23) |
Conformational entropy loss upon association
The entropy loss due to restriction of side-chain dihedral angles upon association (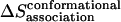
) is calculated by exhaustive enumeration, i.e., sampling each side-chain dihedral angle separately, keeping the backbone atoms and all the other dihedral angles fixed to calculate the effective energy of different conformations, and then calculating the entropy loss of each dihedral angle according to the probability distribution determined from the effective energies. The total side-chain entropy of a TM helix is assumed to be the sum of contributions from each dihedral angle j,
 |
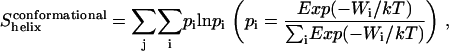(24) |
where pi is the probability of conformation i and Wi is the effective energy for that conformation. Thus the side-chain conformational entropy change upon association is
 |
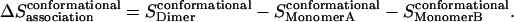(25) |
This method is approximate because it neglects correlations between dihedral angles (the computational cost prevents full enumeration of all dihedral angle combinations). In test calculations where we allowed simultaneous variation of two dihedral angles from neighboring side chains in the dimer, we found that the error due to neglect of correlations is very small (<1%). Secondly, there is an inconsistency in the fact that the average effective energy and the side-chain entropy are obtained based on different conformational ensembles (one from MD, the other by enumeration). However, this is not expected to have a large effect since the energies of different rotamers are rather similar.
Association in micelles
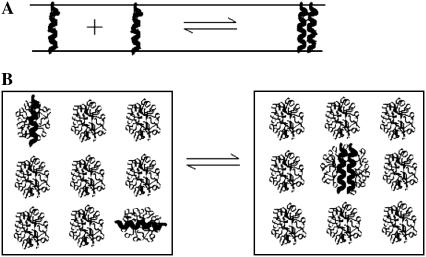
Detergent micelles and lipid bilayers are different in two aspects: a), The shape of the hydrophobic environment is different: the lipid bilayers are roughly a flat slab, whereas the micelles are spherical or elliptical. Given that the helices are fully immersed in the hydrophobic phase, we assume that the effective energy change upon association of TM helices is the same in bilayers and micelles. b), The association entropy of a TM helix in a micelle and a lipid bilayer is different. Before association, the orientation of two monomers is already constrained in the lipid bilayer (Fig. 3 A), whereas any orientation is allowed in a micelle (Fig. 3 B). The translational entropy is also different. Bilayers provide for movement in a continuous, two-dimensional medium, whereas micelles are essentially zero-dimensional media. The movement of the micelle in solution does not contribute to the entropy of the peptide embedded in it. Only the movement of the peptide with respect to the micelle contributes. The translational entropy loss upon association is the sum of two terms: one arising from the overall distribution of helices in micelles and one from the local “vibrations” of the helices within a micelle. The rotational entropy loss occurs because a monomer can rotate freely within a micelle, but two helices in a dimer rotate together. Obviously, association in micelles is very complex and may contain contributions from the detergent itself (if, for example, the aggregation number changes upon association). Here we will perform a very basic calculation under the following assumptions: a), micelles are ideal, spherical objects, and b), each micelle cannot contain more than one monomer or dimer.
FIGURE 3.
Difference in GpA association in a lipid bilayer (A) and detergent micelles (B).
The translational entropy loss upon association due to the distribution in micelles is calculated in the following way. Let CP be the standard concentration (molarity in the hydrophobic phase). The number of micelles per monomer or dimer at the standard concentration is
 |
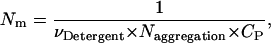(26) |
where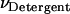 
is the molar volume of hydrophobic tails of pure detergents, which is ∼0.193 L/mol for DPC, and Naggregation is the aggregation number of the micelles. The aggregation number of DPC micelles is ∼50–60 (35); we used 55. For standard concentration 1 M (in HP), Nm is <1, which means 1 M (in HP) standard state in not accessible in practice if each micelle can contain only one monomer or dimer. Therefore, 1 mM (in HP) state is used and the result is corrected by RTln(1000). At 1 mM (in HP), standard state Nm is ∼94. The number of states (Ω) for n indistinguishable protein molecules of the same kind in nNm micelles is
 |
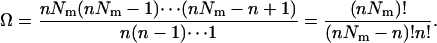(27) |
If n is a very large number, using Stirling's approximation (ln n! 
n ln n – n) gives
 |
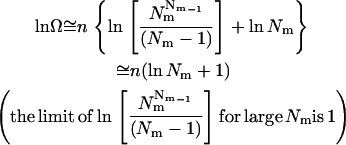(28) |
The 1 in Eq. 28 corresponds to the “communal entropy” discussed above. For the noncovalent association process, 2 Monomers 
Dimer, the standard free energy change upon association can be defined as the free energy change for 2 mol of monomer at 1 mM to convert to 1 mol of dimer at 1 mM. Accordingly, the translational entropy loss upon association due to the distribution in micelles should be
 |
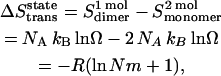(29) |
where NA is Avogadro's number, and kB is Boltzmann's constant. Thus the translational entropy loss due to the decrease of the number of translation states contributes ∼3.3 kcal/mol to the association free energy at 1 mM (in HP) standard state, which corresponds to ∼−0.8 kcal/mol, at 1 M (in HP) standard state.
The translational entropy change due to the constraints inside the micelles includes contributions from the x, y plane (
) and the z axis (
, which is assumed to be the same as in bilayers; see Eq. 15).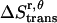 
is equal to the entropy due to the translation of a dimer inside the micelle on the x, y plane (
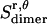), plus the entropy due to the relative translation of one helix with respect to the other in the dimer on the x, y plane (
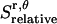), less the entropy due to the translation of monomers A and B inside the micelle on the x, y plane (
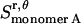and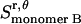 
):
 |
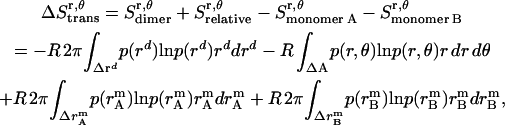(30) |
where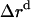 
, 
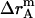, and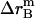 
is the amplitude of 
, 
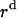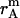, and 
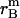, respectively. 
, 
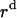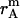, and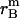 
is the distance of the dimer or monomer from the center of the micelle. 
, 
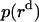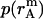, and 
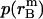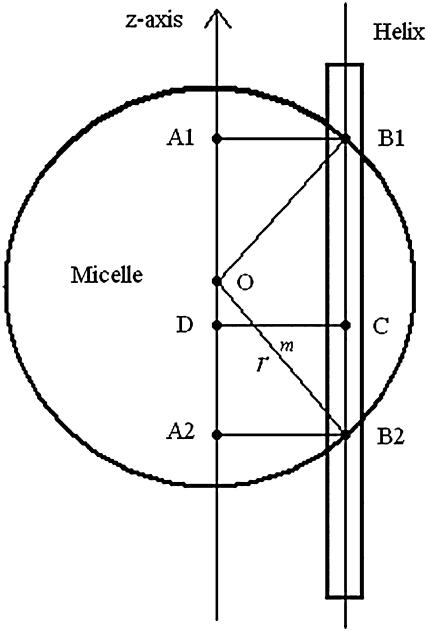
are calculated theoretically according to the energy distribution. ΔA, r, θ, and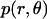 
are the same as those in Eq. 14. As shown in Fig. 4, the hydrophobic burial (T) of a monomer or dimer changes with the distance from the center of the micelle (
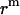). T can be calculated by T = 2
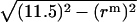, assuming the helix is an ideal cylinder, the hydrophobic core of detergent micelle is an ideal sphere, and the helical axis is parallel to the z axis. So we calculate the effective energy (W) as a function of T using IMM1 and obtain p(rm) as
 |
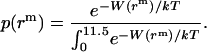(31) |
FIGURE 4.
Translation of GpA monomer inside a micelle. To simplify the problem, a GpA helix and the hydrophobic core of a detergent micelle are presented as a cylinder and a sphere, respectively, and the helical axis is parallel to the z axis (only the cross section is shown). Points O and C are the origin of the coordinate system, and the center of the helix, respectively. Points B1 and B2 are the crossing points of the helical axis and the micelle surface. Points D, A1, and A2 are projections of points C, B1, and B2 on the z axis, respectively. CD equals the distance of the center of a GpA monomer to the origin on the x, y plane,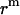 
. OB1 and OB2 denote the radius of the micelle sphere. The radius of the hydrophobic core of the spherical micelle is arbitrarily defined as 11.5 Å since we are using the IMM1 with thickness of 23 Å to mimic the hydrophobic environment of micelles. The thickness of the hydrophobic phase (T) at a distance of 
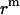is A1A2 (A1A2 = OA1 + OA2 = 2OA1 = 2OA2), thus T = 2
.
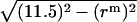Since a 23 Å thick hydrophobic slab of IMM1 model is used to mimic the hydrophobic environment of micelles when the protein is at the center of the micelle,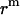 
varies from 0 to 11.5 Å and 
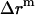is 11.5 Å. 
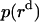, the distribution of a dimer inside the micelle can be calculated similarly.
Thus the total translational entropy change upon association in micelles is
 |
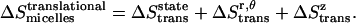(32) |
The method to calculate rotational entropy loss upon GpA association in micelles is the same as that upon binding in water (21):
 |
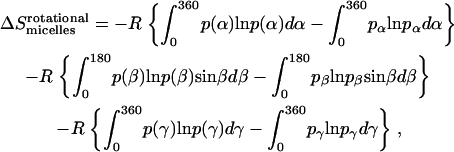(33) |
where α, β, and γ are relative Euler angles of one helix with respect to the other helix (reference helix) in the dimer and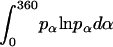 
, 
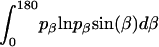, and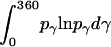 
are the rotational entropy on α-, β-, and γ-dimensions, respectively, corresponding to the free rotation state of a monomer (
, 
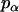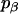, and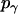 
are constants determined from normalization 
= 
= 
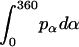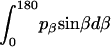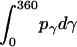= 1). p(α), p(β), and p(γ) are calculated from the bilayer simulations using IMM1.
Since the same effective energy function was used for both bilayers and micelles, we assume that side-chain conformational entropy change upon association is the same in bilayers and micelles.
METHODS
IMM1 model
IMM1 is an implicit membrane model derived from the implicit aqueous model effective energy function 1 (EEF1) (36). It gives the effective energy (WIMM1) of a protein in a heterogeneous membrane-water system as the sum of the intramolecular energy (E) of the protein and the solvation free energy (ΔGslv) (32).
 |
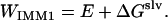(34) |
The intramolecular energy is calculated by the CHARMM 19 polar hydrogen energy function and the solvation energy is the sum of contributions from each atom or group i
 |
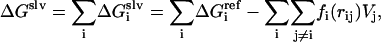(35) |
where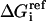 
is the solvation free energy of group i in a small, model compound and the last term is the solvation free energy lost due to exclusion of solvent by surrounding atoms. One essential difference between EEF1 and IMM1 is the definition of reference solvation free energy. In IMM1, the reference solvation free energy depends on the position of each atom with respect to the membrane. The values in the interior of the membrane are obtained from solvation data in cyclohexane:
 |
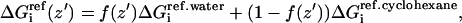(36) |
where z′ =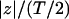 
(T denotes the thickness of hydrophobic core of the membrane) and f(z′) is defined by
 |
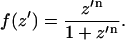(37) |
Normally n is set equal to 10, which gives the appropriate steepness of transition between nonpolar and polar environments (32). f = 0.5 corresponds to the hydrocarbon-polar headgroup interface.
A second difference between EEF1 and IMM1 model is that a modified dielectric screening function is used to calculate the electrostatic interaction in the membrane:
 |
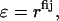(38) |
where fij reflects the positions of the two interacting groups i and j with respect to the membrane and can be calculated by the empirical model
 |
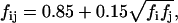(39) |
where fi and fj are defined by Eq. 37.
MD simulations
Two structures of Glycophorin A are available: one was determined by solution NMR in DPC micelles (Protein Data Bank code: 1AFO) (14); the other was obtained by solid-state NMR in DMPC bilayers (15). Here, the initial structures were obtained from the solid-state NMR structure of GpA; 29 residues (from GLU70 to LEU98) were modeled. The N- and C-termini were blocked by acetyl and methylamine groups, respectively. Before MD simulations, the structures were energy-minimized by the Adopted Basis Newton-Raphson (ABNR) method. Nuclear Overhauser effect (NOE) constraints between hydrogen bonded O and N atoms were used to reduce statistical fluctuations and to prevent the changes in the extramembranous portions observed in previous work (32). (A 5-ns simulation of GpA without NOE constraints produced a ∼0.5 Å root mean-square deviation (RMSD) in the interhelical interface, from Leu-75 to Thr-87, with all crucial interhelical contacts maintained). In IMM1, 23.0 Å was used as the hydrophobic thickness because that is close to the hydrophobic thickness of DMPC bilayer (37). All simulations were conducted with the CHARMM package and the Verlet integrator. The temperature of all simulations was set to 298.15 K at which the experimental measurements were normally conducted. During simulations, the average temperature after 0.1 ns was ∼298.0 K and ∼299.2 K for the monomer and the dimer, respectively.
Association free energy calculations
The effective energies during the last 0.9 ns of several 1-ns MD simulations of GpA monomer and dimer in the membrane were averaged and used to calculate the effective energy change upon association. Since NOE constraints generate an artificial additional energy term, this energy term was removed in our effective energy calculations. The magnitude of this term for the first run was ∼10 kcal/mol, ∼4.3 kcal/mol, and ∼1.4 kcal/mol for the dimer, the monomer, and the effective energy change upon association, respectively.
The following steps were followed for the translational entropy calculations:
Run MD simulations of the dimer and the monomers, and save 1000 coordinate frames in each trajectory.
Calculate the coordinates of the center of 21 α-carbon atoms on residues from Thr-74 to Gly-94 with CHARMM command RGYR.
Compute a histogram for each center of mass coordinate using 0.4 Å intervals, normalize it, and calculate the translational entropy loss according to Eqs. 16, 32, and related equations.
The detailed protocol for the rotational entropy calculations is the following:
For each coordinate frame, calculate the coordinates of Point 1 (the center of 21 α-carbon atoms on residues from Thr-74 to Gly-94), Point 2 (the center of 7 α-carbon atoms on residues from Thr-74 to Val-80) and Point 3 (the α-carbon atom on residue Val-84) on the helix of interest with CHARMM command RGYR.
- Determine the angles for the helix rotated about the z (γ) and y axis (β) from the vector of Point 1 (x1, y1, z1) → Point 2 (x2, y2, z2):
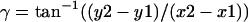
- There are several steps to find α. First, move the whole helix to bring Point 1 to the origin; second, rotate Point 3 about the z axis by an angle –γ; third, rotate Point 3 about the y axis by an angle −(90° − β); finally, α can be calculated from the new coordinates of Point 3 (x3′, y3′, z3′):
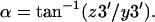
Calculate the range of each Euler angle; count the number of structures in each 5° (β) or 18° (α or γ) interval in that range; normalize the probability distribution in that range; and calculate the rotational entropy loss according to Eqs. 23 or 33 and related equations.
The side-chain conformational entropy was calculated by systematic sampling of each dihedral angle. Since the effective energy is sensitive to translational and rotational configuration of a TM helix (translation on z axis, tilt angle to membrane normal, and rotational angle about the helical axis), side-chain entropies were averaged over 100 frames (after energy minimization) from MD trajectories. For each frame, the side-chain conformational entropy of the monomer or the dimer was calculated according to Eq. 24. The side-chain conformational entropy loss was calculated by Eq. 25 using the average side-chain entropies.
RESULTS
Structural stability of GpA during the MD simulations
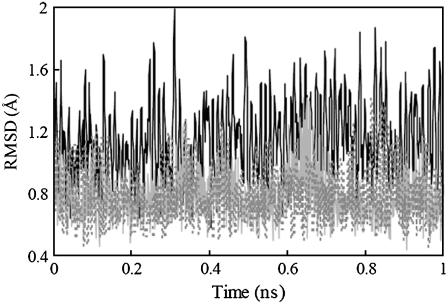
Seven 1-ns MD simulations were performed starting with a different random number for the assignment of velocities. The RMSD of the backbone atoms of monomers and dimer with respect to their initial structures for run No. 1 is shown in Fig. 5. The RMSD of the dimer for most of the simulation time of run No. 1 is <1.6 Å and the RMSD of the monomers is even smaller, which demonstrates that the dimer is sufficiently stable during the simulations. A 5-ns simulation of GpA without NOE constraints was also performed, which produced a ∼0.5 Å RMSD in the crucial part for association, from Leu-75 to Thr-87, although the flanking residues fluctuated considerably.
FIGURE 5.
RMSD of GpA monomers (the gray and solid line for monomer A and the gray and dashed line for monomer B) and dimer (the black and solid line) during 1 ns MD simulations for run No. 1.
Effective energy changes of GpA upon association in bilayers
MD simulations of 29-residue GpA monomers, and the dimer were performed separately to calculate the effective energy change (ΔW) upon association. The results are presented in Table 1. The average effective energies of monomer A and monomer B over several runs are close to each other, as they should. The average effective energy change is −14.9 ± 1.8 kcal/mol, which is much smaller than the average interhelical effective interaction energy of ∼−23 kcal/mol. The difference is accounted for by a change in intrahelical energy (reorganization energy) (21). For run No. 1, the average reorganization energy for the two helices is 7.9 kcal/mol and can be decomposed into 8.9 kcal/mol from van der Waals, 0.3 kcal/mol from electrostatics, −1.6 kcal/mol from solvation, and 0.3 kcal/mol from bonded terms. The contribution of each residue to the reorganization energy and its van der Waals, electrostatics, salvation, and bonded energy components were calculated; the largest contributions are shown in Table 2. Residues 73–76 and 89–92 contribute large solvation terms to the reorganization energy, probably because they are around the hydrophobic-hydrophilic boundary and solvation terms are very sensitive to environment changes that take place upon association. Fig. 6 shows the configuration of the monomer and dimer in the membrane. The tilt of each helix remains the same upon association, but the position on the z axis of each helix shifts ∼1.1 Å toward the C-terminal direction and its rotation is different, which causes effective energy changes for residues 73–76 and 89–92 after association. The large contribution of the van der Waals term to the reorganization energy is probably caused by changes in side-chain conformations. Indeed, the average side-chain conformation of all major contributors to the van der Waals term, except Leu-89, changes upon association.
TABLE 1.
Average effective energy change upon GpA association in a 23-Å lipid bilayer calculated from 1 ns MD simulations (kcal/mol)
| WMonomer A | WMonomer B | WDimer | |
|---|---|---|---|
| Run No. 1 | −516.5 | −516.1 | −1047.1 |
| Run No. 2 | −518.9 | −516.6 | −1049.0 |
| Run No. 3 | −516.5 | −515.9 | −1048.7 |
| Run No. 4 | −515.2 | −516.1 | −1046.7 |
| Run No. 5 | −517.5 | −516.9 | −1049.4 |
| Run No. 6 | −516.8 | −516.7 | −1046.7 |
| Run No. 7 | −516.2 | −516.9 | −1049.6 |
| Average | −516.8 ± 1.2 | −516.5 ± 0.4 | −1048.2 ± 1.3 |
| ΔW | −14.9 ± 1.8 (−27.4, 2.1, 9.9) | ||
Numbers in parentheses are van der Waals, electrostatics, and solvation contributions to ΔW, respectively.
TABLE 2.
Residue contributions to the reorganization energy upon GpA association in a 23-Å lipid bilayer (run No. 1) (kcal/mol)
| Residue | All | VDW | ELEC | SOLV | BOND |
|---|---|---|---|---|---|
| Glu-70 | 1.0 | 0.3 | 0.3 | 0.6 | −0.3 |
| Ile-73 | −2.3 | 1.4 | −1.1 | −1.8 | −0.7 |
| Thr-74 | 2.1 | 0.4 | −0.5 | 2.0 | 0.3 |
| Leu-75 | 2.7 | −0.2 | 0.2 | 3.1 | −0.3 |
| Ile-76 | −2.3 | 0.0 | −0.2 | −2.2 | 0.0 |
| Ile-77 | −2.0 | −1.6 | 0.2 | −0.8 | 0.2 |
| Ile-88 | 1.8 | 1.6 | 0.2 | 0.1 | −0.1 |
| Ile-91 | 4.6 | 0.2 | 0.8 | 3.1 | 0.5 |
| Ser-92 | −2.3 | 0.3 | 0.1 | −2.5 | −0.2 |
| Tyr-93 | 2.1 | 1.0 | 0.1 | 0.5 | 0.5 |
| Ile-95 | 1.5 | 1.4 | −0.1 | 0.3 | 0.0 |
| Arg-96 | 1.0 | 0.4 | −0.1 | 0.3 | 0.5 |
| Total | 7.9 | 8.9 | 0.3 | −1.6 | 0.3 |
VDW, ELEC, SOLV, and BOND are van der Waals, electrostatics, solvation, and bonded components of the reorganization energy, respectively. Only the residues with the largest absolute contributions (≥1 kcal/mol) are shown.
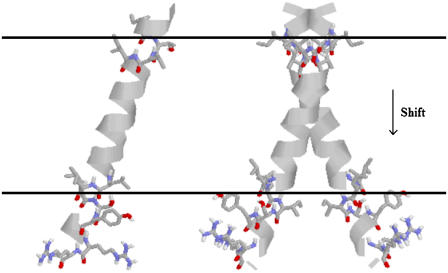
FIGURE 6.
Change in configuration of GpA upon association.
Translational entropy loss of GpA upon association in bilayers
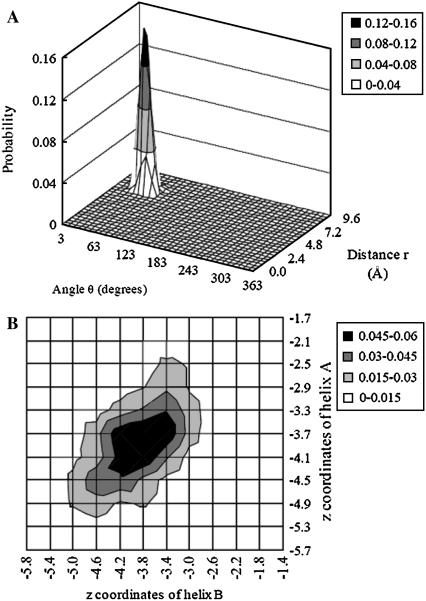
The translational and rotational entropy losses of GpA upon association in bilayers were calculated from MD run No. 1. The contribution of translation entropy change along the x, y plane to the standard free energy is 1.9 kcal/mol. The entropy changes from the x. y plane due to the change of amplitude, uneven distribution, and the change of “communal entropy” are −0.9 kcal/mol, −0.4 kcal/mol, and −0.6 kcal/mol, respectively. The joint probability distribution of relative distance r and angle θ is shown in Fig. 7 A. The contribution from the z dimension is −0.2 kcal/mol. The entropy changes from the z axis due to the change of amplitude and uneven distribution are −0.1 kcal/mol and 0.3 kcal/mol, respectively. The joint probability distribution of z coordinates of helix A and helix B in a dimer is presented in Fig. 7 B. The small positive entropy change from the z axis is mainly due to a flatter probability distribution of the helices in a dimer compared to the monomers.
FIGURE 7.
Joint probability distribution of the relative distance r between two helices and the angle θ in a dimer on the x, y plane (A) and joint probability distribution of the z coordinates of helix A and helix B in a dimer (B). The bin size for distance or z is 0.4 Å and the bin size for θ angle is 10°.
Rotational entropy loss of GpA upon association in bilayers
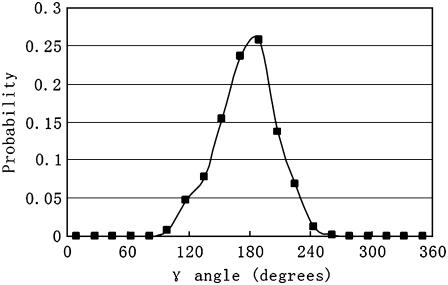
The rotational entropy change upon association in bilayers is −1.4 kcal/mol. The contributions from the γ-angle and from the α- and β-angles are both −0.7 kcal/mol. As expected, the rotational entropy on the γ-rotational dimension decreases since the monomers are free to rotate on that dimension but the relative rotation of one helix to the other in the dimer is restricted by interhelical interactions. Fig. 8 shows the distribution of the γ-angle in the dimer (γ =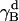 
–
, 
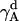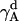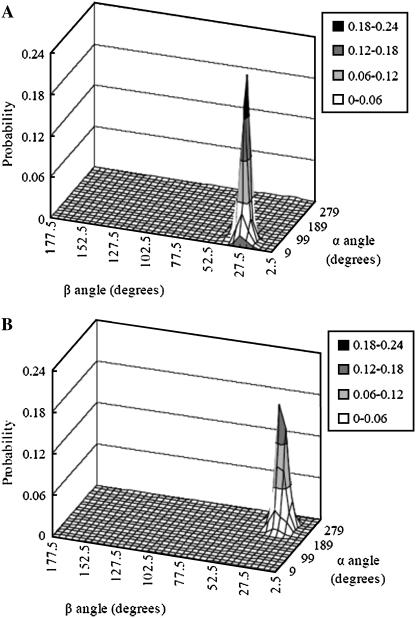
, and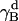 
are Euler angles of helix A and helix B in the dimer with respect to the reference state, respectively). The joint probability distribution of α- and β-angles of helix A as a monomer and in a dimer is shown in Fig. 9. A −0.7 kcal/mol entropy loss was found on these two dimensions, although the coupled distribution in the monomer is sharper than that in the dimer. This indicates that the coupling between the angles of one and the other helix (Eq. 20) is responsible for the entropy loss. The distribution peak is located ∼27.5° on the β-dimension before and after association, but the location of the distribution peak on the α-dimension changes from ∼63° to ∼279° upon association. This reflects what was mentioned above, i.e., the tilt angle remains the same but the rotation angle changes upon association.
FIGURE 8.
Probability distribution of the γ-angle (the difference between helix A and B in a dimer). The bin size is 18°.
FIGURE 9.
Joint probability distribution of α-angle and β-angle of helix A as a monomer (A) and in a dimer (B). The bin size is 18° and 5° for α-angle and β-angle, respectively.
Side-chain conformational entropy loss of GpA upon association in bilayers
The largest contributions are shown in Table 3, and they are from Glu-72 (−0.8 kcal/mol), Leu-75 (−0.7 kcal/mol), Ile-76 (−0.8 kcal/mol), Phe-78 (+0.4 kcal/mol), Ile-91 (−0.5 kcal/mol), Arg-96 (−0.4 kcal/mol), and Arg-97 (−0.9 kcal/mol). The other residues' contributions are <0.3 kcal/mol. Leu-75 and Ile-76 are at the interhelical interface. Glu-72 and Ile-91 are also found at the interhelical interface in the solid-state NMR structure. Therefore it is reasonable that these residues contribute significantly to the conformational entropy loss. Interestingly, Val-80 and Val-84 in the LIxxGVxxGVxxT motif do not contribute significantly to the side-chain conformational entropy. This is consistent with the fact that the deuterium NMR spectra of Val-84 in the monomeric and dimeric GpA peptides are remarkably similar, which indicates there is no conformational entropy loss of these valines upon association due to restriction of the side chain by intrahelical packing interactions involving the β-methyl group of valines (38). Unexpectedly, Phe-78, Arg-96, and Arg-97, which are not at the interhelical interface, contribute considerably to the side-chain conformational entropy. The positive side-chain entropy change from Phe-78 is probably because Phe-78 in the dimer is closer to the center of the hydrophobic core due to the shift of the dimer toward the C-terminus (see Fig. 6), and its nonpolar side chain gains conformational freedom in the dimer. Despite the shift of the dimer, the side chains of Arg-96 and Arg-97 in the dimer are even closer to the interface between polar headgroups and the hydrophobic core due to the change in the α-angle upon association (see Fig. 6), which probably leads to stronger interactions between them and Tyr-93; therefore Arg-96 and Arg-97 in the dimer appear to have less side-chain conformational freedom than they do in the monomer.
TABLE 3.
Side-chain entropy changes of some residues upon GpA association in bilayers (kcal/mol)
| Residue | TΔSside chain | Dihedral | TΔSside chain |
|---|---|---|---|
| Glu-72 | −0.8 | 1 | −0.4 |
| 2 | −0.2 | ||
| 3 | −0.2 | ||
| Leu-75 | −0.7 | 1 | −0.5 |
| 2 | −0.2 | ||
| Ile-76 | −0.8 | 1 | −0.1 |
| 2 | −0.7 | ||
| Phe-78 | 0.4 | 1 | 0.3 |
| 2 | 0.1 | ||
| Ile-91 | −0.5 | 1 | −0.0 |
| 2 | −0.5 | ||
| Arg-96 | −0.4 | 1 | −0.2 |
| 2 | −0.1 | ||
| 3 | −0.1 | ||
| 4 | −0.1 | ||
| 5 | −0.0 | ||
| Arg-97 | −0.9 | 1 | −0.3 |
| 2 | −0.2 | ||
| 3 | −0.4 | ||
| 4 | −0.0 | ||
| 5 | −0.0 | ||
| All 29 residues | −4.1 | ||
The temperature T is 298.15 K. Side-chain entropy changes of the other residues are not shown in this table and their absolute values are <0.3 kcal/mol.
Standard free energy of GpA upon association in bilayers
Table 4 summarizes the results obtained in the previous sections. The favorable change in effective energy (−14.9 ± 1.8 kcal/mol) is partially compensated by the unfavorable translational, rotational, and conformational entropy change to give a value of −7.7 kcal/mol for the standard association free energy of GpA in DMPC bilayers.
TABLE 4.
Standard free energy of GpA upon association in membrane bilayers at 1M (in HP) standard state (kcal/mol); the temperature T is 298.15 K
| ΔW | −14.9 ± 1.8 |
| TΔStrans | −1.7 |
| TΔSrot | −1.4 |
| TΔSside chain | −4.1 |
| ΔG0 at 1 M (in HP) standard state | −7.7 ± 1.8 |
Standard free energy of GpA upon association in micelles
The standard association free energy of GpA in DPC micelles and its components are summarized in Table 5. The effective energy change and side-chain entropy loss are assumed to be the same as in bilayers. The translational entropy change upon association in micelles is less negative because the entropy change due to the change in number of translation states is positive at the (unrealistic) 1 M HP standard state. The rotational entropy loss upon association in micelles is much larger than that in bilayers because before association, monomers in micelles are free to rotate but monomers in bilayers are already rotationally constrained. The standard association free energy of GpA in DPC micelles calculated at 1 M (in HP) standard state is −6.4 ± 1.8 kcal/mol, which is close to −6.1 kcal/mol converted to the same standard state from the experimental value.
TABLE 5.
Standard free energy (kcal/mol) of GpA upon association in DPC micelles at 1 M (in HP) standard state
| ΔW | −14.9 ± 1.8 |
| TΔStrans | −0.4 (0.8, −1.2) |
| TΔSrot | −4.0 |
| TΔSside chain | −4.1 |
| ΔG0 at 1 M (in HP) standard state | −6.4 ± 1.8 |
The temperature T is 298.15 K. Numbers in parentheses are entropy changes due to two terms: one arising from the distribution of helices in micelles and one from the local “vibrations” of the helices within a micelle.
DISCUSSION AND CONCLUSIONS
In this work, the standard association free energy was decomposed into the effective energy change, translational entropy loss, rotational entropy loss, and side-chain entropy loss upon association. The average effective energy change upon association was calculated as −14.9 ± 1.8 kcal/mol, a result of compensation between an interhelical interaction of ∼−23.0 kcal/mol and a helix reorganization energy of ∼7.9 kcal/mol. After the entropic terms were included, the standard association free energy of GpA in DPC detergent micelles was theoretically estimated to be −6.4 ± 1.8 kcal/mol, which is in excellent agreement with the value of −6.1 kcal/mol converted from free energy of association at mole fraction standard state determined experimentally (6). This agreement must be somewhat fortuitous, given the drastic approximations made in the micelle calculation (the effective energy change and side-chain entropy loss in bilayers and micelles were assumed to be the same; the micelle was treated as an ideal sphere; contributions from the detergent were neglected).
Because micelles are convenient for quantitative studies, it is important to understand the difference in association in micelles and bilayers. Our calculations showed that the translational and rotational entropy changes upon association are different in bilayers and in micelles. The contribution of translational entropy to the association free energy in bilayers and micelles is 1.7 kcal/mol and 0.4 kcal/mol, respectively. The reason for the smaller translational entropy loss in micelles could be that, because of the spherical nature of micelles, and the requirement of only one monomer per micelle, much micelle volume remains inaccessible to the monomer. That is, a monomer in a certain micellar hydrophobic volume has less entropy than in an equal amount of bilayer hydrophobic volume, because bilayers are continuous. In contrast, the rotational entropy change in micelles is ∼2.6 kcal/mol less favorable than in bilayers, because the monomers are preoriented in bilayers but are free to rotate in micelles. Assuming that these are the only factors that are different between the two media, the calculated standard association free energy in DMPC bilayers is ∼1.3 kcal/mol more favorable than in DPC micelles. This is consistent with the experimental observations that the association of GpA appears stronger in membrane bilayers in vivo than in detergent micelles (10) and that the difference in association constant of M2 protein in DMPC bilayers and DPC micelles corresponds to more than 0.7 kcal/mol for each helix-helix interface (17). Another relevant observation is that certain epidermal growth factor receptors helices have been found to associate in vivo, but not in micelles (2).
In terms of structural changes upon association, we found that the rotation angle changes upon association but the tilt angle remains the same. This differs from the results of Henin et al. (26), who proposed that change of tilt is coupled with helix-helix recognition. A possible reason for the discrepancy is that the tilt of the monomers observed by Henin et al. was smaller than in our study, perhaps due to the increased thickness of their membrane, whereas the tilt of the helices in the dimer by their and our calculations is almost the same due to interhelical interactions. Thus, the change of tilt in their calculations is larger than ours.
Henin et al. (26) estimated the association free energy of GpA by integrating the potential of mean force as a function of the distance between the helices. They obtained the value −11.5 kcal/mol. The standard state implicit in their calculation is 1 molecule/Å2 (22), which, for 26 Å hydrophobic thickness, corresponds to 63.8 M (in HP) in our standard state. The conversion of their value to our standard state can be done by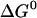 
= 
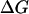+ RT × lnC (C = 63.8M) and gives ∼−9.0 kcal/mol, not very different from ours. Henin et al. find that van der Waals and solvation make about equal contributions to the association free energy. We, however, find that van der Waals is the only favorable force, and solvation is unfavorable to association (see Table 1). The origin of this discrepancy is unclear. It seems more sensible that the removal of lipids from contact with the associating helices should be unfavorable. It would help if the solvation contribution computed by Henin et al. could be resolved into water and organic solvent components.
It is useful to also compare the present results with those of Lomize et al. (25). The effective energy change upon association was decomposed into −27.4 kcal/mol from van der Waals, 2.0 kcal/mol from electrostatics, 9.9 kcal/mol from solvation, and 0.3 kcal/mol from bonded terms. These values are larger than those of Lomize's. However similar energetic aspects are shown in both calculations: 1), van der Waals is the major driving force for association; and 2), electrostatics and solvation energies are not favorable for association. The reorganization energy was neglected in their calculations, as well as the translational and rotational entropy changes. The side-chain conformational entropy loss we obtained is much larger than the 0.9 kcal/mol that Lomize et al. (25) calculated, because they do not consider contribution from residues that are not at the interhelical interface.
Grasberger et al. (39) investigated the effect of restricted mobility on protein association in membrane, and their results showed that restriction of translation and rotation in membrane can enhance protein dimerization by 4300 and 132 times, respectively, compared to dimerization in aqueous solution. These two enhancements correspond to 4.8 kcal/mol and 2.8 kcal/mol. The enhancement from translational restriction refers to the difference between bulk concentration and local concentration in the membrane, including excluded volume effects, and is not relevant to our study. The rotational restriction enhancement of 2.8 kcal/mol is very similar to our calculation of 2.6 kcal/mol difference in rotational entropy loss between bilayers and micelles. They assumed a maximum tilt of 10°, although from our MD simulations the tilt angle of monomers could be more than 30°. Also the tilt angle distribution from our simulation is much wider than what they estimated.
It has been demonstrated that MD simulations based on IMM1 can estimate the standard association free energy of TM helices in bilayers and micelles and illustrate possible translational, rotational, and conformational changes upon association. This work opens the way to quantitative investigations of the driving forces of TM helix association and de novo predictions of the propensity of TM helices to associate.
Acknowledgments
We thank Dr. M. Mottamal for helpful discussion.
This work was supported by the National Science Foundation (MCB-0316667). Infrastructure support was provided in part by RCMI grant RR03060 from the National Institutes of Health.
References
- 1.Popot, J., and D. Engelman. 1990. Membrane protein folding and oligomerization: the two-stage model. Biochemistry. 29:4031–4037. [DOI] [PubMed] [Google Scholar]
- 2.Stanley, A., and K. Fleming. 2005. The transmembrane domains of ErbB receptors do not dimerize strongly in micelles. J. Mol. Biol. 347:759–772. [DOI] [PubMed] [Google Scholar]
- 3.Fleming, K. G., A. L. Ackerman, and D. M. Engelman. 1997. The effect of point mutations on the free energy of transmembrane alpha-helix dimerization. J. Mol. Biol. 272:266–275. [DOI] [PubMed] [Google Scholar]
- 4.Fleming, K. G. 2002. Standardizing the free energy change of transmembrane helix-helix interactions. J. Mol. Biol. 323:563–571. [DOI] [PubMed] [Google Scholar]
- 5.Fleming, K. G., C. C. Ren, A. K. Doura, M. E. Eisley, F. J. Kobus, and A. M. Stanley. 2004. Thermodynamics of glycophorin A transmembrane helix dimerization in C14 betaine micelles. Biophys. Chem. 108:43–49. [DOI] [PubMed] [Google Scholar]
- 6.Fisher, L. E., D. M. Engelman, and J. N. Sturgis. 1999. Detergents modulate dimerization, but not helicity, of the glycophorin A transmembrane domain. J. Mol. Biol. 293:639–651. [DOI] [PubMed] [Google Scholar]
- 7.Fisher, L. E., D. M. Engelman, and J. N. Sturgis. 2003. Effect of detergents on the association of the glycophorin a transmembrane helix. Biophys. J. 85:3097–3105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Brosig, B., and D. Langosch. 1998. The dimerization motif of the glycophorin A transmembrane segment in membranes: importance of glycine residues. Protein Sci. 7:1052–1056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Russ, W. P., and D. M. Engelman. 1999. TOXCAT: a measure of transmembrane helix association in a biological membrane. Proc. Natl. Acad. Sci. USA. 96:863–868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Langosch, D., B. Brosig, H. Kolmar, and H. J. Fritz. 1996. Dimerisation of the glycophorin A transmembrane segment in membranes probed with the ToxR transcription activator. J. Mol. Biol. 263:525–530. [DOI] [PubMed] [Google Scholar]
- 11.Lemmon, M. A., J. M. Flanagan, J. F. Hunt, B. D. Adair, B. J. Bormann, C. E. Dempsey, and D. M. Engelman. 1992. Glycophorin A dimerization is driven by specific interactions between transmembrane alpha-helices. J. Biol. Chem. 267:7683–7689. [PubMed] [Google Scholar]
- 12.Lemmon, M. A., J. M. Flanagan, H. R. Treutlein, J. Zhang, and D. M. Engelman. 1992. Sequence specificity in the dimerization of transmembrane alpha-helices. Biochemistry. 31:12719–12725. [DOI] [PubMed] [Google Scholar]
- 13.Lemmon, M. A., H. R. Treutlein, P. D. Adams, A. T. Brunger, and D. M. Engelman. 1994. A dimerization motif for transmembrane alpha-helices. Nat. Struct. Biol. 1:157–163. [DOI] [PubMed] [Google Scholar]
- 14.MacKenzie, K. R., J. H. Prestegard, and D. M. Engelman. 1997. A transmembrane helix dimer: structure and implications. Science. 276:131–133. [DOI] [PubMed] [Google Scholar]
- 15.Smith, S. O., D. Song, S. Shekar, M. Groesbeek, M. Ziliox, and S. Aimoto. 2001. Structure of the transmembrane dimer interface of glycophorin A in membrane bilayers. Biochemistry. 40:6553–6558. [DOI] [PubMed] [Google Scholar]
- 16.DeGrado, W. F., H. Gratkowski, and J. D. Lear. 2003. How do helix-helix interactions help determine the folds of membrane proteins? Perspectives from the study of homo-oligomeric helical bundles. Protein Sci. 12:647–665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Cristian, L., J. D. Lear, and W. F. DeGrado. 2003. Use of thiol-disulfide equilibria to measure the energetics of assembly of transmembrane helices in phospholipid bilayers. Proc. Natl. Acad. Sci. USA. 100:14772–14777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kim, S., A. K. Chamberlain, and J. U. Bowie. 2003. A simple method for modeling transmembrane helix oligomers. J. Mol. Biol. 329:831–840. [DOI] [PubMed] [Google Scholar]
- 19.Helms, V., and R. C. Wade. 1998. Computational alchemy to calculate absolute protein-ligand binding free energy. J. Am. Chem. Soc. 120:2710–2713. [Google Scholar]
- 20.Froloff, N., A. Windemuth, and B. Honig. 1997. On the calculation of binding free energies using continuum methods: application to MHC class I protein-peptide interactions. Protein Sci. 6:1293–1301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lazaridis, T., A. Masunov, and F. Gandolfo. 2002. Contributions to the binding free energy of ligands to avidin and streptavidin. Proteins. 47:194–208. [DOI] [PubMed] [Google Scholar]
- 22.Gilson, M. K., J. A. Given, B. L. Bush, and J. A. McCammon. 1997. The statistical-thermodynamic basis for computation of binding affinities: a critical review. Biophys. J. 72:1047–1069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Horton, N., and M. Lewis. 1992. Calculation of the free energy of association for protein complexes. Protein Sci. 1:169–181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lazaridis, T. 2002. Binding affinity and specificity from computational studies. Curr. Org. Chem. 6:1319–1332. [Google Scholar]
- 25.Lomize, A. L., I. D. Pogozheva, and H. I. Mosberg. 2004. Quantification of helix-helix binding affinities in micelles and lipid bilayers. Protein Sci. 13:2600–2612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Henin, J., A. Pohorille, and C. Chipot. 2005. Insights into the recognition and association of transmembrane alpha-helices. The free energy of alpha-helix dimerization in glycophorin A. J. Am. Chem. Soc. 127:8478–8484. [DOI] [PubMed] [Google Scholar]
- 27.Petrache, H. I., A. Grossfield, K. R. MacKenzie, D. M. Engelman, and T. B. Woolf. 2000. Modulation of glycophorin A transmembrane helix interactions by lipid bilayers: molecular dynamics calculations. J. Mol. Biol. 302:727–746. [DOI] [PubMed] [Google Scholar]
- 28.Feller, S. E., K. Gawrisch, and T. B. Woolf. 2003. Rhodopsin exhibits a preference for solvation by polyunsaturated docosohexaenoic acid. J. Am. Chem. Soc. 125:4434–4435. [DOI] [PubMed] [Google Scholar]
- 29.Braun, R., D. M. Engelman, and K. Schulten. 2004. Molecular dynamics simulations of micelle formation around dimeric glycophorin a transmembrane helices. Biophys. J. 87:754–763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Beevers, A. J., and A. Kukol. 2006. Systematic molecular dynamics searching in a lipid bilayer: Application to the glycophorin A and oncogenic ErbB-2 transmembrane domains. J. Mol. Graph. Model. 25:226–233. [DOI] [PubMed] [Google Scholar]
- 31.Bond, P., and M. S. Sansom. 2006. Insertion and assembly of membrane proteins via simulation. J. Am. Chem. Soc. 128:2697–2704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lazaridis, T. 2003. Effective energy function for proteins in lipid membranes. Proteins. 52:176–192. [DOI] [PubMed] [Google Scholar]
- 33.Sesta, B. 1989. Physicochemical properties of decyldimethylammonium propanesulfonate and its homologous compounds in aqueous medium. J. Phys. Chem. 93:7677–7680. [Google Scholar]
- 34.Henchman, R. H. 2003. Partition function for a simple liquid using cell theory parametrized by computer simulation. J. Chem. Phys. 119:400–406. [Google Scholar]
- 35.le Maire, M., P. Champeil, and J. V. Moller. 2000. Interaction of membrane proteins and lipids with solubilizing detergents. Biochim. Biophys. Acta. 1508:86–111. [DOI] [PubMed] [Google Scholar]
- 36.Lazaridis, T., and M. Karplus. 1999. Effective energy function for proteins in solution. Proteins. 35:133–152. [DOI] [PubMed] [Google Scholar]
- 37.de Planque, M. R., and J. A. Killian. 2003. Protein-lipid interactions studied with designed transmembrane peptides: role of hydrophobic matching and interfacial anchoring. Mol. Membr. Biol. 20:271–284. [DOI] [PubMed] [Google Scholar]
- 38.Liu, W., E. Crocker, D. J. Siminovitch, and S. O. Smith. 2003. Role of side-chain conformational entropy in transmembrane helix dimerization of glycophorin A. Biophys. J. 84:1263–1271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Grasberger, B., A. P. Minton, C. DeLisi, and H. Metzger. 1986. Interaction between proteins localized in membranes. Proc. Natl. Acad. Sci. USA. 83:6258–6262. [DOI] [PMC free article] [PubMed] [Google Scholar]