Reconstitution of the Frank-Starling Mechanism in Engineered Heart Tissues

Abstract

According to the Frank-Starling mechanism, as the heart is stretched, it increases its contraction force. Reconstitution of the Frank-Starling mechanism is an important milestone for producing functional heart tissue constructs. Spontaneously contracting engineered heart tissues (EHTs) were reconstituted by growing dissociated chicken embryo cardiomyocytes in collagen matrices. Twitch and baseline tensions were recorded at precisely controlled levels of tissue strain. The EHTs showed a steep increase in twitch tension from 0.47 ± 0.02 to 0.91 ± 0.02 mN/mm² as they were stretched at a constant rate (2.67% per min) from 86% to 100% of the length at which maximum twitch force was exerted. In response to a sudden stretch (3.3%), the twitch tension increased gradually (∼60 s) in a Gd³⁺-sensitive manner, suggesting the presence of stretch-activated Ca²⁺ channels. A large difference in baseline tension between lengthening (loading) and shortening (unloading) was also recorded. Disruption of nonsarcomeric actin filaments by cytochalasin D and latrunculin B decreased this difference. A simple mechanical model interprets these results in terms of mechanical connections between myocytes and nonmuscle cells. The experimental results strongly suggest that regulation of twitch tension in EHTs is similar to that of natural myocardium.

INTRODUCTION

When cardiac ventricular filling increases so that the wall of the ventricle is stretched, the contraction force of the heart and therefore its stroke volume increases correspondingly according to the Frank-Starling mechanism. This important functional property of the heart supplies an essential regulatory mechanism by which cardiac output is intrinsically optimized relative to demand. Skeletal muscle also displays a length-dependent increase of developed tension, which is explained mainly as a result of changing the degree of overlap of thick (myosin) and thin (actin) filaments, i.e., in terms of the number of functioning myosin cross-bridges. The rate at which developed tension changes with tissue length in cardiac muscle is much steeper than that in skeletal muscle (1), indicating that a different mechanism relates length and developed tension in the heart. This steepness originates from the length dependence of 1), the degree of Ca²⁺ release from the sarcoplasmic reticulum, and 2), the change in Ca²⁺ sensitivity of the contractile apparatus (2). A recent observation suggests that the dependence of the Ca²⁺ sensitivity on stretch can be explained in terms of a length-dependent change in lateral spacing between thin and thick filaments, but other mechanisms may also contribute (3). The Frank-Starling mechanism has been observed even in severely damaged human myocardium (4). The developed force at a given resting tension in the damaged heart, however, becomes significantly smaller than that of normal heart. To produce a twitch force similar to that observed in normal myocardium, the damaged heart muscle must be stretched much more.

The scientific and potential clinical utility of reconstituted cardiac constructs has been demonstrated by several groups (5–11). In this work, we have investigated systematically the Frank-Starling mechanism in engineered heart tissues (EHTs) under various conditions. We have observed a strain-dependent increase in twitch force produced in EHTs made using chicken embryo cardiomyocytes. There is a steep dependence of developed tension on stretch, similar to that seen in natural myocardium. The slow increase (∼60 s) in twitch force in response to a quick stretch of an EHT suggests the existence of a length-dependent Ca²⁺ sensitivity similar to that observed in the natural tissue (12). We have also observed that twitch force increases when the baseline force is increased by activation with serum. In our constructs as in natural heart muscle, there are many nonmuscle cells (especially fibroblasts), which could contribute to the serum response and in general could have a large influence on both the baseline and twitch tensions produced by the EHTs. The disruption of cytoskeletal as opposed to sarcomeric actin filaments also reveals differential effects of nonmuscle cells and cardiomyocytes on developed tension. These results systematically demonstrate the existence of the Frank-Starling mechanism in EHTs as suggested earlier (13).

MATERIALS AND METHODS

EHT preparation and mechanical measurements

Cardiomyocytes were isolated from 10-day-old chicken embryos as described previously (5). The formulation of ring-shaped EHTs was almost identical to that of fibroblast-populated collagen matrices described before (14). Briefly, cardiomyocytes (1.4 million/ml, final concentration) were mixed with a solution of collagen (1 mg/ml, final concentration, Type I from rat tail, Upstate, Charlottesville, VA) in culture medium (DMEM with 10% FBS and 4% chicken embryo extract). The cell suspension was poured into a Teflon casting well composed of an outer cylinder and a central mandrel and cast to form a ring (3 mm thick, 3 cm circumference). When the suspension in the well was incubated at 37°C, 5% CO₂, the collagen polymerized within 15–30 min. Then, the EHT was removed from the well, stretched between two rods of a stainless steel spacer (Fig. 1 A), and was immersed in the culture medium. This facilitates diffusion of medium and O₂ into the collagen matrix more freely than can occur in the casting well. The cells compress this ring, reducing its volume ∼10-fold, reaching a final thickness of 200–300 μm in ∼6 days (Fig. 1 B). Spontaneous twitches of isolated cardiomyocytes and synchronized contractions were observed on the third and sixth days of culture, respectively. The ring was removed from the spacer and then mounted on the measuring device described previously (14). The mounted ring was then immersed in an organ bath with HEPES-buffered DMEM at 37°C. The force transducer coupled to the ring rapidly registers changes in contractile force of both the baseline and twitch forces exerted by EHTs. In measurements of the response to strain, an EHT was stretched by the stepper motor-driven mechanism (14) uniaxially to 20% strain in 7.5 min (loading phase) and then relaxed back to the initial zero strain over the same time period (unloading phase).

FIGURE 1.

EHT culture in a petri dish. (A) A schematic drawing of a ring-shaped EHT suspended on stainless steel rods with a spacer inserted (arrow) between the bases of the rods. (B) A photograph of two EHTs cultured in a petri dish, with inch scale shown at left.

Observation of cytoskeletons, quantitative image analysis, and size of EHTs

Previously described methods of immunohistochemistry and imaging of cytoskeletal proteins were used (15). Specific monoclonal antibodies (9D10, Developmental Studies Hybridoma Bank, University of Iowa) (1/100 ascites) were used to label titin. F-actin was stained using rhodamine-conjugated phalloidin (0.5 μg/ml). The cross-sectional images were generated by a previously described method (14). In images taken at lower magnification such as Fig. 2 D, cytoskeletal staining fills the entire cytoplasm. Therefore, the fraction of myocytes (titin is present only in myocytes) in the total cell population (assuming F-actin is in both myocytes and nonmuscle cells) was estimated as (pixels corresponding to titin)/(pixels corresponding to actin) (14). Sample widths of EHTs were measured using a caliper. The thickness of the sample was determined by focusing on both surfaces of the construct with an inverted microscope (IM-35, Carl Zeiss) with calibrated focus control. At the completion of the above mechanical measurements, the samples were fixed in the unloaded state.

FIGURE 2.

Cellular and cytoskeletal distributions in an EHT. The distribution of F-actin stained by rhodamine phalloidin at the edges (A and C) and middle region (B) of an EHT. Distribution of titin (green) and F-actin (red) at the edges (D and F) and middle (E) of cross sections. (G) Spread titin-positive myocytes near the surface of midregion. (H) Almost no spread cells are seen in the center of the midregion. (I)Well spread and connected titin-positive and -negative cells are distributed near the surface of edge. (J)Titin-positive myocytes are almost exclusively distributed in the center of an edge. (Scale bars for A–F and G–J are 100 μm and 16 μm, respectively.)

Disruption of the actin cytoskeleton

F-actin was disrupted using 2 μM cytochalasin D (Sigma, St. Louis, MO) or 10 μM latrunculin B (Molecular Probes, Eugene, OR) as described previously (16).

Estimating sarcomere length by fast Fourier transform

Spontaneously contracting EHTs were stretched to different levels of strain and fixed with 4% paraformaldehyde in phosphate-buffered saline. Sarcomeric titin was visualized using a monoclonal antibody described above. The periodic intensity profile along a straight line drawn over the sarcomeres was obtained using Image J (National Institutes of Health, Bethesda, MD). The spatial frequency of the periodic intensity changes was analyzed using a fast Fourier transform available as a macro in the Origin data analysis software (Northampton, MA). The sarcomere length was estimated from the spatial period obtained by FFT analysis of at least three different images.

RESULTS

Distribution of cells in EHT

Fig. 2, A–C, shows actin cytoskeletons stained with rhodamine-phalloidin visualized at low magnification at different parts of an EHT. Fig. 2, A and C, shows elongated myocytes at both edges of the EHT. The cells in the internal region of the construct shown in Fig. 2 B are sparse, less spread, and not oriented with the long axis of the construct. Cross sections (on planes normal to the edges) of Fig. 2, A–C, are shown in Fig. 2, D–F, respectively. The muscle-specific protein titin, stained with fluorescein-labeled titin-specific antibodies, appears green (Fig. 2, D–J). Actin filaments stained with rhodamine-phalloidin are red (Fig. 2, D–J). Fig. 2, G and H, shows actin and titin in the internal region of the EHT in Fig. 2 B at higher magnification. More cells are localized in a section very close to the surface (Fig. 2 G) than in an inner section (Fig. 2 H) near the center of the construct (a stack of sections forms a three-dimensional volume). Fig. 2, I and J, show actin and titin in cells close to the edge of the sample at higher magnification than those in Fig. 2 C. Near its surface, the EHT is highly populated by groups of myocytes forming fibrils running parallel to the edge of the construct (Fig. 2 I). Many cells in this image were not stained by the titin antibody (Fig. 2 I). These cells may be fibroblasts or endothelial or smooth muscle cells that were not eliminated by the differential adhesion (17) during isolation of the myocytes (18). Cells located far from the surface (inner section) at the edge (Fig. 2 J) were mostly titin positive and were well spread and also closely grouped together, but at a lower density than those near the surface. The ratio of the area occupied by myocytes divided by that of total cells was calculated in each of 52 cross-sectional images parallel to each of Fig. 2, D–F. The average ratios of 52 images parallel to each of Fig. 2, D–F, were 41.4 ± 7.1%, 63.7 ± 10.6%, and 71.7 ± 7.4%, respectively. We observed similar results in samples made at various times. Because the density of myocytes is between 1.062 and 1.082 mg/ml (17) of the percoll gradient, which is greater than the densities of other cells, they tend to settle down faster than the other cells at the bottom of casting wells during collagen gel polymerization. Therefore, one side of the sample almost always had a higher proportion of myocytes relative to fibroblasts than the other.

Response of EHT to serum activation and actin filament disruption

Although our analysis of the Frank-Starling mechanism specifically concerns the variation of twitch force with changes in strain and strain-dependent baseline tension of EHTs, activation of nonmuscle myosin by agonists or disruption of the cytoplasmic actin cytoskeleton can also change the baseline tension and influence the twitch force. These responses provide information about the contributions of nonmuscle cells to the contractile behavior of the EHT. That activation by receptor-mediated agonists can increase both baseline and twitch forces was demonstrated when an EHT was treated with 20% (v/v) calf serum (CS) while being held at constant length (Fig. 3 A). The baseline force quickly increased and reached its steady level in 60 min (Fig. 3 B). A slight but reproducible decrease in twitch force immediately after activation was followed by a biphasic increase. Even after 60 min, the twitch force was still increasing at a constant rate (Fig. 3 C) and finally reached a steady level after 120 min (result not shown). It was likely that nonmuscle cells contributed directly to the almost twofold increase in baseline force shown in Fig. 3. The nonmuscle cells could also have played an indirect role in the increase in twitch force. We have previously shown that tissue stiffness is linearly related to the baseline force in reconstituted tissues made with chicken embryo fibroblasts (14). We saw similar results in EHTs (results not shown). The contraction of nonmuscle cells in an EHT could amplify the twitch force generated by the myocytes by increasing the stiffness of the construct. For instance, this would occur if the cardiomyocytes and nonmuscle cells were mechanically connected in series. We simulated this scenario using a simple mechanical model described below.

FIGURE 3.

(A) Serum activation and cytochalasin D (CD) treatment of an EHT. Raw data of baseline and twitch forces increasing in response to addition of calf serum (20% v/v). Separate traces of baseline force (B) and twitch force (C) computed from raw data. The two traces have different shapes, and the baseline force reached its steady level before the twitch force. (D) Raw data of baseline and twitch forces responding to CD treatment (2 μM). The baseline force (E) dropped faster and nearly to zero, whereas the twitch force (F) leveled at ∼30% of its initial value.

As we have shown previously (5), EHTs are sensitive to cytochalasin D (CD), which is known to disrupt the actin cytoskeleton by binding to the barbed (rapidly polymerizing) ends of actin filaments and preventing farther polymerization (19). The CD (2 μM) treatment decreased the baseline force and twitch force within 40–60 min (Fig. 3 D). The baseline force was abolished almost entirely (Fig. 3 E), whereas the twitch force was reduced to ∼30% of its original level (Fig. 3 F). The same concentration of CD eliminates all the active contractile force generated by fibroblasts (16). Microscopic observation of rhodamine-labeled actin in cardiomyocytes grown in a monolayer and treated by CD confirmed that sarcomeric structures (responsible for generating twitch force) remained after the CD treatment (result not shown).

Length-dependent change in baseline and twitch force of EHTs

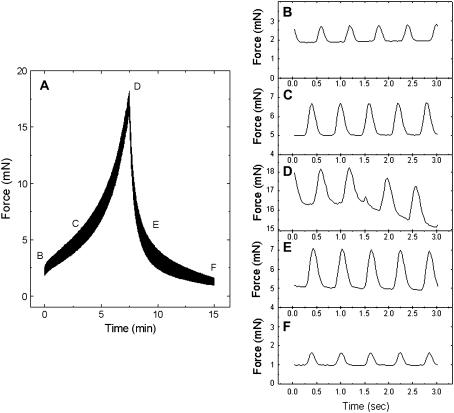
The ability of the heart to contract more strongly in response to an increased load or strain is known as the Frank-Starling mechanism (20). To observe this mechanical property unique to the myocardium, the EHTs were stretched uniaxially up to 20% of their original length (loading phase) and relaxed back from the peak to 0% strain (unloading phase) at a constant strain rate (2.6%/min) for both loading and unloading. The cardiac twitches appeared as an unresolved band on the time scale shown in Fig. 4 A. The baseline force (lower edge of the force band) changed nonlinearly in response to a linear increase and decrease of tissue length (Fig. 4 A). Various parts of the band indicated by the letters in Fig. 4 A were expanded to show individual twitches (Fig. 4, B–F). The duration of the twitch cycles was ∼600 ms, and this was unchanged during the loading and unloading phases of stretching the EHT. The magnitudes of the twitches increased as the EHT was stretched from low (Fig. 4 B) to medium (Fig. 4 C) and to the highest levels (Fig. 4 D) of strain. The twitch force decreased with decreasing strain of the tissue from the highest to medium (Fig. 4 E) and to the lowest level (Fig. 4 F) of strain. At the same baseline force level, the twitch forces measured during unloading (Fig. 4 E) were noticeably larger than those recorded during loading (Fig. 4 C).

FIGURE 4.

Length-dependent change in baseline and twitch forces. (A) Nonlinear changes of baseline and twitch forces recorded during loading and unloading as the EHT is stretched at a constant rate and then unloaded at the same rate. Individual twitches indicated by the letters B–F in A.

The baseline and twitch forces were separately plotted against strain in Fig. 5. As observed with fibroblast-populated constructs (14), the baseline force observed during the loading phase (solid circles) was significantly higher than that observed during unloading phase (open circles) (Fig. 5 A). The hysteresis area enclosed by the two curves represents the energy dissipated by the viscous resistance to stretch of the EHTs. A similar plot was obtained for the twitch force (Fig. 5 B), yet the area of hysteresis was much smaller than that of the baseline force. The magnitude of viscous resistance depends on the rate of deformation of the sample relative to the characteristic rates of the viscous processes in the system (21). It is difficult to compare the strain rates of the twitch and the stretching cycle because the former occurs at constant tissue strain and so involves local deformations within the construct. Nevertheless, the twitch tension developed much faster (∼100 ms) than the stretching cycle (30 min), and so the viscous resistance of the EHT to the rapid twitching could be much smaller than the viscous resistance to the slow stretch.

FIGURE 5.

Hysteresis of baseline and twitch forces. (A) In serum-activated EHTs, the baseline force recorded during loading (solid circles) increased nonlinearly and was significantly higher than that recorded during unloading (open circles). (B) The twitch force of the loading phase increased almost linearly up to 15% strain and was a little higher than that of the unloading phase. (C) CD treatment decreased the baseline force and the area of hysteresis. (D) Twitch force still increased almost linearly up to 15% of strain even with CD treatment. (E) At the same value of the baseline force, the twitch force was higher during unloading than during loading in a plot of twitch force versus baseline force (analogous to a cardiac function curve) of a serum-activated EHT. (F) The traces of both loading and unloading curves coincide after CD treatment. Error bars in all traces are standard errors of four samples.

Similar curves were observed with the same samples used above treated with 2 μM CD for 60 min. Although the baseline force was almost eliminated by CD at low strain, the twitch force was still observed, although with reduced amplitude (Fig. 5, C and D). CD treatment caused a substantial reduction of the hysteresis area for the baseline force, but this is associated with a large reduction in peak force. With this force reduction taken into account, there was no significant difference in the damping energy, a normalized hysteresis area calculated as the ratio of the hysteresis area divided by the area under the loading curve (total energy input) (14). Moreover, CD had no significant effect on the difference in twitch force between loading and unloading. The twitch force was increased by stretching the EHTs, thereby stiffening the construct (see above explanation and Discussion). Similar results were observed using latrunculin-B (LA-B), also known to disrupt nonmuscle F-actin by sequestering actin monomers (results not shown). Therefore, Frank-Starling behavior was also observed in constructs in which the nonsarcomeric actin cytoskeleton was disrupted. The cardiac-specific sarcomeric structure, which was not strongly disrupted by the CD or LA-B treatments, is, therefore, mainly responsible for the Frank-Starling mechanism.

Twitch force plotted as a dependent variable of baseline force clearly shows the dependence of cardiac contractility on preload (Fig. 5 E). Therefore, this plot is analogous to the cardiac function curve, which is a plot of cardiac output or developed pressure versus cardiac filling pressure. The cardiac function curve graphically represents the mechanical function of the heart and can distinguish a normal from a failing heart (22). Before CD treatment, the curve obtained during the loading phase of the EHT had smaller magnitudes of force and slope than those obtained during the unloading phase. Therefore, the contractile activity of the EHT was stronger after the construct had been stretched and while the imposed force was decreasing. After the CD treatment, the contractility of the EHT was still increased by increasing the preload. Yet, the difference between the curves observed during loading and unloading disappeared (Fig. 5 F). This suggested that the difference observed before the CD treatment may depend on the presence of the F-actin network in nonmuscle cells, CD-sensitive nonsarcomeric actin in cardiomyocytes, or possibly sarcomeric actin filaments at an early stage of myofibrillogenesis in cardiomyocytes (23).

Because the EHTs were not externally stimulated during the experiment, the relationship between twitch force and rate of twitching could be examined during stretching. The time period between two consecutive twitches was calculated with using a macro language routine with Origin. The mean peak-to-peak time was calculated by simple average of 800–900 peak-to-peak times. There was no apparent change in the peak-to-peak time during the loading and unloading phases of at least three independent experiments (data not shown). There was also no significant difference in peak-to-peak time before and after CD treatment (data not shown). This indicates that the changes in twitch force observed during the stretching were not caused by changes in the frequency of twitching.

EHT response to a quick stretch

Because Frank-Starling behavior can be regarded as a dependence of twitch force on stretch, measurements of the temporal relationship between twitch force and stretch could provide clues about the mechanism of the process. For example, an immediate increase in twitch force with stretch would be consistent with a structural interpretation, such as a dependence of twitch force on stretch-dependent cross-bridge overlap. A delay in the response of twitch force on stretch, however, would be consistent with a time-dependent activation mechanism such as a stretch-dependent change in Ca²⁺ sensitivity (2). In the isolated rat heart, for instance, the developed pressure increases gradually over minutes on stretching the myocardium by increasing the resting pressure (12). This result was interpreted as indicating a stretch-dependent sensitivity of the Ca²⁺ dependence of twitch contraction. To test the temporal relationship between stretch and twitch force, an EHT was held at constant strain for at least 1 h to establish a steady baseline force, and then the strain was increased by 3.3% within a few seconds (Fig. 6 A). The baseline force increased suddenly and relaxed gradually to establish a new steady level. The twitch force, however, did not follow this pattern. Rather, it increased gradually to establish a new steady level over ∼100 s (Fig. 6 B). This result suggests that the EHT also has a stretch-dependent activation mechanism such as a stretch-activated Ca²⁺ channel. To test this hypothesis, we repeated the quick stretch experiments with media containing Gd³⁺, a known inhibitor of stretch-activated channels (24). Treatment of an EHT with GdCl₃ (5 μM) for 30 min before the quick stretch inhibited a significant portion of the slow increase in twitch force (Fig. 6 C) compared to its control while having no effect on twitch force before stretch. We should note that the medium for these experiments does not contain any 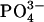or because Gd³⁺ binds very strongly to these anions (25).

FIGURE 6.

Force response to a quick stretch. (A) When the EHT was quickly stretched (3.3% strain in ∼2–3 s), a rapid increase in baseline force was followed by a slow relaxation. A trace of baseline force shows stress relaxation after the sudden force jump. (B) The twitch force increased gradually to its new steady state in 60–120 s. (C) Presence of GdCl₃ in the organ bath inhibited most of the twitch-force increase after a quick stretch. The first point after the stretch was used to normalize the data for comparison.

External Ca²⁺ concentration shifts Frank-Starling curves

When the heart operates in physiological situations, it follows a family of Frank-Starling curves depending on the inotropic state and pre- and afterload. We previously reported an increase in twitch forces produced by isometrically held EHTs by adding incremental doses of Ca²⁺ (5). This phenomenon is often described as “positive inotropic effect”, and skeletal muscle does not demonstrate this effect to a significant degree. To demonstrate a positive inotropic effect in the reconstituted system at various levels of preload, EHTs were stretched, and a family of Frank-Starling curves were recorded in media containing various concentrations (1.8, 2.8, and 3.8 mM) of Ca²⁺. Fig. 7 clearly indicates that increasing the external Ca²⁺ concentration shifts the Frank-Starling curve upward and leftward, as expected in conditions of positive inotropic effect.

FIGURE 7.

Dependence of Frank-Starling curve on Ca²⁺ concentration. Frank-Starling curves were shifted up by increasing concentrations of Ca²⁺ in the organ bath from 1.8 mM to 2.8 mM and to 3.8 mM.

EHT strain correlates with sarcomere length

A correlation between EHT length and sarcomere length (SL) was determined to confirm that the length-dependent increase in twitch force observed in EHTs is directly related to an increase of SL. The spontaneously contracting EHTs were held at the original tissue length or stretched to 121% of the original length. After being held at the appropriate length for a few minutes, samples were fixed with 4% paraformaldehyde. Sarcomeric titin in the fixed EHTs was fluorescently labeled by a monoclonal antibody and fluorescence-labeled secondary antibodies (Fig. 8 A). Fig. 8 B shows the variation of fluorescence intensity due to the periodic sarcomeric organization of the titin in the region indicated by the white bracket (Fig. 8 A). The spatial frequency of the periodicity was analyzed using fast Fourier transform (FFT) (26) and was used to calculate SL (Fig. 8 C). The SL of a 21% strained EHT was 19.1% longer than that of a nonstretched EHT (Table 1), and the range of SL obtained from the experiments matched well with the values of cardiac SL published elsewhere (26). The data shown in Table 1 were obtained from duplicate samples.

FIGURE 8.

Sarcomere length by Fourier analysis. (A) Sarcomeres in myocytes grown in an EHT were visualized by scanning confocal microscopy after fluorescence staining of titin. (B) An intensity profile is plotted along a straight line shown by the square bracket. (C) A strong peak (∼0.525 1/μm) shown in the frequency domain of the intensity profile (0.19 μm) indicates the sarcomere periodicity and yields a value of the sarcomere spacing. (D) Comparison of nonstretched (0%) and stretched (1%) sarcomere were visualized. The fluorescence peaks counted from the edge of the image to the vertical yellow line were 20 and 18–19 in nonstretched and in stretched sample, respectively. (Bar = 4 μm).

TABLE 1.

Sarcomere length determination by image analysis

Strain (%)	SL (μm) ± SD	n
0	1.88 ± 0.16	6
21	2.24 ± 0.16	8

DISCUSSION

Engineered cardiac tissue constructs can provide models for heart development and remodeling, test systems for studies of cardiac tissue mechanics and the regulation of contractility, and ultimately implantable materials for the repair of heart damage. To be useful for these purposes, it is essential that the mechanical properties of EHTs match those of normal heart muscle. An increase of contractile force in response to an increase of strain, Frank-Starling behavior, is a characteristic feature of myocardial mechanics that is essential for normal heart function. Hence, it is important both to demonstrate that EHTs retain this behavior and to analyze its structural and mechanistic characteristics.

Mechanical properties of EHTs, I: Comparison to skeletal muscle and adult myocardium

The force generated by the spontaneous twitches of an EHT increased as the construct was stretched, exhibiting a qualitative similarity to the behavior of natural myocardium described by the Frank-Starling law. Baseline and peak tensions increased nonlinearly (Figs. 4 and 5). The twitch tension ranged from ∼0.47 ± 0.02 to ∼0.92 ± 0.02 mN/mm² (n = 4 each time, repeated at least three times) while the EHT was stretched up to 20% strain (Fig. 9 B). This was significantly lower than the developed tension observed in human tissue samples (∼15–22 mN/mm²) (4). The maximum twitch tension developed by EHTs in this study was similar to that (1 mN/mm²) observed in EHTs that were subjected to mechanical conditioning (18). The baseline tension observed in this study was severalfold higher than the twitch tension, which is opposite to that observed in natural tissue. Mechanical conditioning reduces the baseline tension and improves construct mechanical function and structure (18). It is reasonable to attribute the difference from natural tissue in the ratio of twitch to baseline force to low myocyte and high nonmuscle-cell density, but this is highly speculative at this point.

FIGURE 9.

Comparison of length-dependent mechanical properties of skeletal and cardiac muscle (27) and an EHT. (A) Peak (solid circles) and resting (open circles) tensions of a serum-activated EHT. (B) Length-dependent change in twitch force of an EHT. (C) Length–tension traces of EHTs treated with either serum (open circles) or cytochalasin D (solid circles) were much closer to that of cardiac muscle (solid line) than that of skeletal muscle (dashed line).

The steep dependence of developed tension on stretch is unique to heart muscle, as observed in cat papillary muscle, and is distinct from skeletal muscle (27), which has a much weaker dependence at high strain, as shown in Fig. 9 C. The data from the EHT had a steep slope at high strain similar to that of natural heart muscle. This indicates the reestablishment in the EHT of the stretch–tension relationship unique to the myocardium. The slow increase (∼60 s) in twitch force observed in response to a quick stretch (Fig. 6) resembles that observed in rat atrium (12). This suggests that in EHTs, as in the heart, a length-dependent change in Ca²⁺ sensitivity contributes to the dependence of twitch force on strain.

Mechanical properties of EHTs, II: Contribution of nonmuscle cells

A dependence of developed force on baseline force is not uniquely a response to applied mechanical stretch. We have observed that twitch tension also increases in response to an increase in baseline tension stimulated by calf serum (Fig. 3, A–C). Furthermore, twitch tension decreases along with baseline force in response to disruption of cytoskeletal actin filaments by CD (Fig. 3, D–F) and LA-B. Nonmuscle cells in the EHTs are likely to strongly influence both of these effects on twitch force.

This and previous investigations have observed significant numbers of nonmuscle cells in EHTs, which are present mainly because it was not possible to completely separate myocytes from fibroblasts by differential adherence (17). The cross-sectional area occupied by nonmuscle cells in EHTs used for this work was ∼40% of total cell area (Fig. 2, D–F). Therefore, fibroblasts could have a strong influence on the baseline force and the stiffness of the EHTs both under basal conditions and in response to serum (14). Based on its demonstrated effect on fibroblasts in tissue constructs (14,16), cytochalasin D (CD, 2 μM) was used to eliminate the mechanical contribution of the nonmuscle cells to the EHTs. Indirect evidence suggests that the effect of CD was mainly through its action on nonmuscle cells. Even after CD treatment, the dependence of twitch force on strain resembled that of cardiac rather than skeletal muscle (Fig. 9 C). Although CD (1 μM) treatment has been shown to reduce contractility of single rat adult myocytes (28), no substantial reduction of sarcomeric actin structures by CD (2 μM) was observed in EHTs by phalloidin staining. Therefore, even though CD treatment has removed the mechanical contributions of the nonmuscle cells and the twitch force has substantially diminished, a significant twitch force amplitude remains. This indicates that the cardiomyocytes can exert force on the surroundings of the construct via linkages in parallel to the nonmuscle cells via the matrix. Nevertheless, the nonsarcomeric actin cytoskeleton of myocytes may have been partially disrupted, and the contractility of myocytes may have been somewhat reduced, by the CD treatment. Latrunculin B (LA-B) is also known to disrupt F-actin networks by sequestering actin monomers (16). The baseline force of EHTs was abolished by the treatment with 20 μM LA-B as with CD. The twitch force was reduced by the LA-B treatment from 345 ± 71 μN (n = 26*) to 96 ± 3 μN (n = 30*), whereas the twitch force treated by 2 μM CD reduced from 352 ± 55 μN (n = 31*) to 48 ± 7 μN (n = 38 (average of n twitches of two samples)). The sarcomeric structure of cardiomyocytes was insensitive to microinjection of DNase I (29), which in analogy with LA-B acts by sequestering actin monomers. The different susceptibilities of twitch force to the CD and LA-B treatments may be related to the different mechanisms of action of these drugs. Nevertheless, the smaller effect of LA-B on twitch force suggests a milder effect of actin monomer sequestration on cardiac contractility.

The fibrotic myocardium formed after myocardial infarction contains activated cardiac fibroblasts (30). The EHT tested here may mimic myocardium with fibrosis. As a preliminary study, EHTs were made adding grater cardiac fibroblast content (additional 25% of total cells). These constructs developed less twitch force and significantly higher baseline force than those of control EHTs. The Frank-Starling curve of the EHT with extra cardiac fibroblasts was shifted down and to the right. This trend in shifting the Frank-Starling curve is similar to that observed in papillary muscles harvested from human hearts with cardiomyopathy (4).

A mechanical model simulates Frank-Starling curves of EHTs

Similar to mechanical measurements of passive (diastolic) myocardium (31), the mechanical measurements of passive (baseline force) EHTs showed viscoelastic behavior. Because we observe similar hysteresis curves in consecutive stretches, this may differ from the phenomenon known as strain softening, caused by unrecoverable damage to the sample by strain (31). In contrast to intact tissues, it is relatively easy to measure various mechanical properties of a live EHT under physiological conditions. In this study, active cardiac twitches as well as passive mechanical properties of EHTs were measured simultaneously at various strain levels (Fig. 5). To the best of our knowledge there are no similar experimental data for natural myocardium. In an EHT, the passive viscoelasticity influences active cardiac contraction. When the passive (baseline) force was increased by activation or decreased by disruption of nonmuscle cells (Fig. 3) under isometric conditions, the active (twitch) force changed correspondingly. This suggests that myocytes may be connected mechanically in series with nonmuscle cells to sense the force produced by them. To test this hypothesis, a mathematical model was developed to simulate the viscoelastic behavior of an EHT. This model is based on a mechanical model that simulates the viscoelastic behavior of fibroblasts in a tissue construct (32). To account for twitch contraction, a twitch-force generator was simply inserted next to the element that represents nonmuscle cells.

The mathematical model, described in the Appendix, consists of three elements: A), a contractile element that generates cardiac twitches, B), an active nonlinear viscoelastic element that represents active fibroblasts, and C), a passive nonlinear viscoelastic element that represents the passive extracelluar matrix (ECM) (Fig. 10). The model is still phenomenological; therefore, assignments of the elements to specific cell types and ECM should be considered as approximations at this level of simulation. Nevertheless, the addition of a variable time constant into element B (Eq. 2, Table 2) allowed this model to simulate the rapid force drop observed during the unloading phase (Figs. 5 A and 11 A). The Frank-Starling mechanism was built into the twitch generator (element A) as a stress-dependent increase in twitch force. By including the delayed response of twitch force after rapid stretch (Fig. 6 B) in the mathematical model (Appendix, Eq. 1), the higher twitch force observed during the unloading phase (Fig. 5 C) was simulated (Fig. 11, B and C).

FIGURE 10.

Schematic of the biophysical model for an EHT. The model consists of a twitch-force generator representing cardiac myocyte mechanics (A), a Hill element simulating fibroblast mechanics (B), and a Kelvin-Voigt viscoelastic solid characterizing the mechanics of extracellular matrix (C).

TABLE 2.

Parameters used for mathematical simulation shown in Fig. 11

Twitch	Cell		Matrix
f50=2.25 mN	K1 =17 mN/strain	τf = 200 s (dɛ/dt > 0)	km1 = 4.25 mN/strain
τm=50 s	K2 =68 mN/strain	τf = 46 s (dɛ/dt < 0)	km2 = 17 mN/strain
ft=3 mN	τc =200 s		ɛnl = 8%
	f0 =2.5 mN		τm = 200 s

FIGURE 11.

Mathematical simulations of EHT mechanical properties. Curves in A, B, and C simulate the experimental data shown in Fig. 5, A, B, and E, respectively. Loading and unloading parts of the curves are shown as solid black and light gray, respectively. By introducing a time delay of the response of the cardiac twitch to stretching, the model simulated the loop in which twitch force during unloading exceeded that during loading, seen at high strain, and a slight nonlinearity of the dependence of twitch force on strain at low strain (B). The model also successfully approximated the dependence of baseline force on strain (A) and of twitch force on baseline force (C).

Summary and future improvements and applications of EHT

The presence of active fibroblasts in the EHTs influences the mechanical properties measured in this study. Nevertheless, the EHTs successfully reproduced Frank-Starling behavior in various calcium concentrations. Remarkably similar to the natural myocardium, the EHT responded slowly to a sudden stretch, which partly depended on stretch-activated channels sensitive to Gd³⁺. A simple mathematical model taking into account the nonlinear viscoelastic nature of nonmuscle cells and the delayed response of twitch force to stretch simulated the hysteresis of twitch force observed during a cycle of loading and unloading.

The distribution and density of cardiomyocytes within EHTs have a decisive influence on the mechanical properties of the constructs. In our EHTs, the overall density of cardiomyocytes was much less than that observed in the heart, and most of the myocytes were concentrated at the edges of the constructs (Fig. 2). To produce EHTs that better mimic the structure and mechanical function of heart muscle, the myocyte density and functional integration (gap- and adherens-junction connections) should be increased. A number of factors could contribute to this needed improvement. We have observed that freshly prepared chicken embryo extract (Materials and Methods) increased the magnitude of EHT twitches. Mechanical conditioning by cyclic stretching increases the myocyte density and induces a more homogeneous distribution of myocytes in EHTs (18) beyond what we have observed in our constructs (Fig. 2). To increase the density of myocytes and increase their contractile force and tissue strength, the EHT needs a vascular system to deliver necessary nutrients and oxygen to the myocytes. Perfusion of medium through developing cardiac constructs has been shown to improve the density of myocytes grown in biodegradable scaffolds (33). Another crucial requirement for the development and maintenance of mechanical function is to control the population and mechanical contributions of fibroblasts in EHTs. The continuing physiological characterization and improvement of EHTs are critical steps toward applying the technology in drug discovery (34,35).

APPENDIX: MATHEMATICAL MODEL

Force produced by the twitch-force generator depends on force generated by nonmuscle cells, i.e., force applied to the twitch-force generator. Therefore, the generator produces twitch forces of amplitude T depending on the applied force f with response delay-time constant τ_m. A differential equation that represents time-dependent T is

(1)

where t is time, f₅₀ is a half-maximum force Frank-Starling relationship, and f_t is a scaling factor that relates T and f.

The active and passive contributions of nonmuscle cells to the baseline force were modeled using a Hill-type model with nonlinear springs whose constants k₁ and k₂ vary depending on the given strain ɛ (Fig. 10 B). The time-dependent force response of the element B (Fig. 10) can be expressed mathematically as

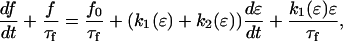(2)

where τ_f is the relaxation constant of element B. Tissue constructs made from fibroblasts show an exponential increase in stiffness with stretching (14). Therefore, we define k₁ and k₂ as

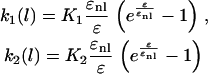(3)

where K₁ and K₂ are the initial stiffness of the springs, and ɛ_nl represents the strain at which the nonlinearity starts. Experiments (Fig. 5 A) showed a marked decrease in the relaxation time, τ_f, when strain rate, dɛ/dt, became negative (unloading phase). Therefore, we chose different relaxation times for the loading and unloading phases. The extracellular matrix was assumed to be a Kelvin-Voigt viscoelastic solid, which can be obtained from Eq. 2 by setting f₀ = 0. The parameters used for simulation (Fig. 10) are listed in Table 2.