Analysis of Single-Molecule FRET Trajectories Using Hidden Markov Modeling

Abstract

The analysis of single-molecule fluorescence resonance energy transfer (FRET) trajectories has become one of significant biophysical interest. In deducing the transition rates between various states of a system for time-binned data, researchers have relied on simple, but often arbitrary methods of extracting rates from FRET trajectories. Although these methods have proven satisfactory in cases of well-separated, low-noise, two- or three-state systems, they become less reliable when applied to a system of greater complexity. We have developed an analysis scheme that casts single-molecule time-binned FRET trajectories as hidden Markov processes, allowing one to determine, based on probability alone, the most likely FRET-value distributions of states and their interconversion rates while simultaneously determining the most likely time sequence of underlying states for each trajectory. Together with a transition density plot and Bayesian information criterion we can also determine the number of different states present in a system in addition to the state-to-state transition probabilities. Here we present the algorithm and test its limitations with various simulated data and previously reported Holliday junction data. The algorithm is then applied to the analysis of the binding and dissociation of three RecA monomers on a DNA construct.

INTRODUCTION

Fluorescence resonance energy transfer (FRET) is a powerful method for uncovering many mechanistic aspects of biological macromolecules and complexes. Acting as a spectroscopic ruler, FRET provides information on the distance between two points of a system to which a donor fluorophore and an acceptor fluorophore are attached. If the biomolecules under investigation are localized in space, for example through tethering to a surface, FRET signals can be obtained even from single molecules for an extended period. The data obtained from such experiments, time traces, are composed of a triplet at each time point: (donor signal and acceptor signal versus time). Each trace is often converted to (FRET versus time) pairs which we term FRET trajectories. In the case of well-defined, stable conformational states a corresponding series of well-defined stable FRET values can be observed. The analysis of time-binned FRET trajectories should ideally determine what conformational states exist in the system and with what rates interconversion between the states occurs.

To accomplish this, historically one needed to determine, based on the FRET values, which state the system was in at a given time and for how long it remained there. Typically, histograms were built out of the resulting dwell times and then fit to an exponential decay (1–7). The method of deciding when the molecule is in what state can vary from simplistic “by eye” analysis to the slightly more sophisticated thresholding algorithm. In the “by eye” case (6), one determines, based on one's own experience, what changes in FRET are legitimate state-to-state transitions as opposed to noise or photophysical effects. In this approach, shorter transitions are likely to be missed and the results may vary from person to person. The other common approach is the thresholding algorithm (8) that requires a user to set cutoffs between FRET states. Still needed is a way of distinguishing a noise-induced change in FRET from a legitimate short-lived transition, and one needs to account for the fact that different molecules, even from an entirely homogenous population, can show different state FRET values due to instrumental noise. In both cases, analysis is performed with a preconceived number of states in mind and is subject to the user's prejudice for systems of great complexity. Likewise in both cases the ability to reliably and reproducibly analyze data becomes almost impossible when the number of states being analyzed increases beyond three. To overcome the shortcomings of these approaches we have devised an algorithm based on hidden Markov modeling that seeks to determine in a probabilistic and less user-dependent way the number of conformational states of a system and the rates of exchange between them.

BASIS OF THE ALGORITHM

Hidden Markov modeling (HMM) was developed originally to aid in speech recognition but has expanded to a variety of different fields. For a concise review of the basic principles of HMM, see Eddy (9). In the realm of biophysics, such modeling has been used extensively in the analysis of ion-channel data (10,11), and very recently for single-molecule fluorescence data (12–15). Though these single-molecule fluorescence algorithms have proven extremely powerful for determining dynamics with high precision and on very short timescales, they suffer from requiring photon arrival times using a point detection apparatus such as a silicon avalanche photodiode. Here we present an algorithm that utilizes the time-binned data obtained from the higher throughput wide-field apparatus, where single-molecule data are obtained for hundreds of molecules at the same time using a CCD camera (16,17) though in fact it could be applied to any time-binned data regardless of origin.

A Markov process consists of any combination of state-to-state transitions with kinetics governed by single-exponential decay. A Markov process becomes hidden when an observer's ability to detect states is obscured by noise. Let us consider a system that can adopt one of two conformational states (A or B), where the probability of observing state A transit to state B in one time step is governed by single exponential decay and independent of how long the molecule has been in state A. If a FRET pair has been placed on the molecule such that the ideal, noiseless FRET values obtained from each state are FRET_A and FRET_B (Fig. 1 A), in principle, one could obtain a molecule's true A↔B trajectory by following the FRET value in time as it alternates between FRET_A and FRET_B (Fig. 1 B). In reality, experimental noise broadens the FRET distribution of each state (Fig. 1 C) yielding significantly more complicated data (Fig. 1 D). This makes the process a hidden Markov process as the underlying reality (the sequence of true A↔B exchanges) is hidden in the data because of noise. To reconstruct the underlying reality using HMM, first we need to define model parameters.

FIGURE 1.

Simple single-molecule FRET hidden Markov process. (A) A molecule exhibits two different FRET states: FRET_A and FRET_B. For each time point, there is a probability (tp) that it will transit to the other state. A noiseless system would generate simple two-state FRET trajectories (B). But a distribution in FRET values (C) masks the idealized sequence of states, hiding the underlying Markov process (D). In italics are the parameters one would not know in a real experiment but would eventually want to obtain, namely: the idealized FRET states (FRET_A and FRET_B), the state-to-state transition probabilities (tp), and the distribution of observed data for the FRET states (width).

The transition probability matrix and emission probability functions

Parameters of HMM analysis are described typically by transition and emission probabilities. In the two-state system described above transition probabilities represent the probability of a molecule currently in state φ (either A or B) transiting to state ψ (either A or B) in the next time step, in general called tp_φ→ψ. Of the total of four transition probabilities (tp_A→B, tp_A→A, tp_B→A, and tp_B→B) forming a transition probability matrix (Fig. 2 A), only two are independent since by definition tp_A→A + tp_A→B = 1 and tp_B→B + tp_B→A = 1. It is important to note that in using a transition probability matrix of this form one is implicitly assuming that the underlying process is a Markov process. This means that transitions are assumed to be governed by single exponential decay kinetics.

FIGURE 2.

Evaluating probabilities in a hidden Markov model. (A) The transition probability matrix gives the likelihood that a molecule in one state will transit to another in a single time step. (B) Emission probability functions (ep_A, ep_B) define the probability of observing a FRET value FRET_data when in a given conformation (A or B). The emission probability functions and the transition probability matrix shown are for a known two-state system with underlying FRET values 0.3 and 0.7 (state A and state B, respectively) and a width in the distribution of 0.16, similar to the system depicted in Fig. 1. (C) Generated data (squares) are plotted together with a proposed sequence of states (α₁(i)). By using the parameters from A and B, we can evaluate the probability that the proposed sequence could generate the observed data for each time point and then take their product to find the total. (D) The same is done for an alternative proposed sequence of states (α₂(i)) with differences highlighted in bold and underlining. By comparing the total probabilities of 1343 for α₁(i) to that of 1193 for α₂(i) we deduce that a transition likely took place at time step 3.

Emission probabilities represent the relative likelihood of observing a FRET value (FRET_data) when the system is in conformation φ (with idealized FRET value FRET_φ). We have modeled the noise-induced FRET distribution using a Gaussian function with a characteristic width δ. Then, the two emission probability functions (ep_A and ep_B) are given as follows:

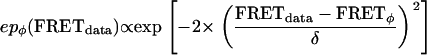(1)

Although FRET distributions are in fact governed by β-distributions rather than simple Gaussians, it has been found that such distributions are approximated well by Gaussians, an assumption which leads to minimal discrepancies (18).

Deciding between different event sequences

Once we have a transition probability matrix and emission probability functions for a system we can evaluate the relative likelihood of any proposed sequence of A and B states given the observed data FRET_data(i) (where i represents time step). We term the time-indexed proposed sequence of states α so that α(i) = A or B. To evaluate how likely a proposed sequence α is we calculate, for each time point, the probability that the proposed state yields our observed data (using the emission probability function), and then determine the point's transition probability to the next time step's proposed state. Multiplying the two terms we obtain the probability of the proposed state yielding the observed data at that time point:

(2)

The probability of the entire proposed trajectory is obtained by multiplying the individual point probabilities:

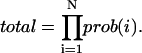(3)

As a specific example, we provide the seven-time point-trajectory in Fig. 2. The system follows the parameters in Fig. 1 but with a narrower width (δ = 0.16 instead of δ = 0.35). Fig. 2, C and D, attempts to fit the same set of data with two different proposed trajectories. In Fig. 2 C, the proposed trajectory α₁ has a transition from B to A in time step 3 and the reverse in time step 4. In the trajectory α₂ proposed in Fig. 2 D no transition takes place. To determine which of the two is the most likely given the model parameters in Fig. 2, A and B, we use Eqs. 2 and 3. Although it is much more likely for a molecule in state B to remain in state B as in the trajectory α₂ than to transit from state B to state A and then back again as in α₁, it is even more likely for a molecule in state A to emit a FRET value at 0.39 as in α₁ than a molecule in state B to as in α₂. Thus, the more likely trajectory among the two is α₁.

To try every possible sequence of states and find the total probability for a FRET trajectory of N time points would require O(2^N) computational power for a two-state system. Fortunately this can be cut down to O(N) using the Viterbi algorithm (19), which is guaranteed to find the most likely sequence of underlying states given a set of data and corresponding transition probability matrix and emission probability functions.

Determining emission probability functions and transition probability matrices

Thus far we have assumed that the emission probability functions and transition probability matrix are known beforehand. But in an experiment, one does not usually know the idealized FRET_A, FRET_B values or their distributions. In addition, the transition probabilities are what one is after in the first place. As the Viterbi algorithm also provides the total probability of the most likely sequence of states, we can vary the model parameters (FRET_A, FRET_B, δ, tp_A→B and tp_B→A) until we achieve a maximized total probability. This is a well known multi-dimensional optimization problem which we solved using Brent's algorithm (20). We have found that as long as reasonable first guesses are made with respect to the parameters the algorithm converges to the true values rather than to a local maxima. As initial guesses, we use uniform transition probabilities of 0.005 and uniformly distributed FRET states between 0 and 1, or rough estimates based on the data. Similar results could in principle be obtained with other HMM algorithms such as the faster but more complicated Baum-Welch forward-backward algorithm (21). All algorithms were encoded in C++ and analysis performed on the UIUC Turing CPU cluster.

Utilizing multiple trajectories

In the hopes of obtaining a more accurate tp_A→B and tp_B→A, one would generally like to determine them for a number of different molecules and then find some way to average them. We have found that transition probabilities are distributed asymmetrically as in Fig. 3 A. Therefore to obtain a representative average value and corresponding uncertainty we first take the transition probabilities returned from the HMM algorithm and find their logarithm (as in Fig. 3 B). The logarithm is chosen partially for because it yields symmetry, but also because of the relationship between free energy and kinetic rates: 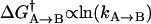. That is, if the free barrier has heterogeneous broadening that is symmetric, the distribution of the logarithm of the transition rate would be symmetric. Once the logarithm has been taken, a mean is determined together with its standard error. These are then converted back to transition probabilities by exponentiation. Explicitly, for a collection of N transition probabilities labeled by i:

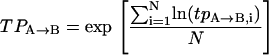(4)

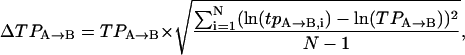(5)

where TP_A→B and ΔTP_A→B denote the representative mean and the representative error, respectively.

FIGURE 3.

Compiling data from multiple FRET trajectories. (A) Histograms built out of transition probabilities found using the HMM algorithm for experimental data show that the data are not distributed symmetrically, bunching around 0.01 with some points all the way out at 0.2. To determine the real value, we first transform the transition probabilities into log or ΔΔG space (B) where the data is distributed symmetrically. From here, the mean and standard error is calculated and converted back into transition probabilities using Eqs. 4 and 5.

Transition density plot for complicated systems

Note that in the algorithm outlined above, there is nothing to restrict ourselves to two-state systems. For any FRET trajectory with S underlying FRET states there are S × (S−1) independent transition probabilities, S idealized FRET state levels, and a width parameter δ. We chose a single value of δ for all states to reduce computational time.

It is often the case that the value of S itself is unknown. In such cases the solution is simple: assume some large number of states (say M = 10) and perform analysis. If there are in reality only five states (S = 5), five legitimate (between 0 and 1) FRET values and their associated transition probabilities will be returned together with five extraneous states. The extraneous states are never populated.

Another potential difficulty in systems with a large number of states is one of how to categorize FRET states. Let us consider an example of a five-state system (states labeled A, B, C, D, and E). In some cases individual FRET trajectories may not show all five states (for instance, if the trace is not long enough). Or the FRET values found for each individual state may not agree completely between trajectories (one molecule's state A may have an apparent FRET = 0.25, whereas for another molecule it may have an apparent FRET = 0.2 due to experimental variability). Occasionally one might even see an additional state, C′, which was found by the algorithm but differs only slightly from one of the existing states C.

To visualize the number of actual FRET states (S) in a way that avoids these pitfalls, we developed a simple two-dimensional pseudo-histogram we call the transition density plot (TDP). For each FRET trajectory analyzed (where the algorithm attempted to fit M different states), the algorithm finds M idealized FRET_m levels (m = 1, 2, …, M), the transition probability matrix, and the number of transitions found for each of the FRET_m → FRET_m* pairs of FRET levels. A two-dimensional Gaussian function is constructed for each pair of start and stop FRET values (start_m, stop_m), with an amplitude (a_m,m*) equal to the number of transitions found that started at start_m and ended at stop_m* and width σ (we chose σ² = 0.0005 empirically to yield clear plots). Summing each Gaussian over all state combinations (start_m, stop_m*) in all traces yields the TDP, with the horizontal axis corresponding to the starting FRET values and the vertical axis corresponding to the final FRET values:

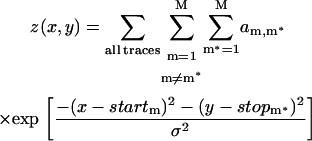(6)

The advantage of this method can be seen in the example of Fig. 4. The simulated FRET trajectory in Fig. 4 A shows no peaks when a histogram is constructed out of its FRET values (Fig. 4 B). But if there are distinct, reproducible FRET values from trace to trace, then peaks should develop in the TDP (Fig. 4 C). For a general S-state system with exchange possible between every state, S × (S − 1) peaks should appear.

FIGURE 4.

Simulated five-state system and its TDP. (A) A typical trace from a five-state system is fit with the modeling algorithm. Nonphysical FRET values >1 and <0 are a simulation artifact and do not impact hidden Markov modeling. (B) Just looking at the FRET values alone it is impossible to determine where FRET states are. (C) After compiling hundreds of fit traces a TDP is generated. The starting FRET position is graphed on the bottom (x axis) and ending FRET position is graphed on the left (y axis). The graph is obtained by summing up Gaussian functions for every transition found, with centers corresponding to the initial (x) and final (y) FRET value for the transition. (D) Once peaks are discerned, their number can be determined, along with their positions and widths.

Determining the number of underlying states

Although the TDP is a useful visual tool for making an initial guess as to the number of underlying FRET states in a system, it is preferable to have some way of determining that number in a fully probabilistic manner. For this we remove the smoothing introduced by converting individual points into Gaussians and revert to a simple scatter plot showing the location of all transition pairs found for each individual molecule as in Fig. 5 A. Here each spike corresponds to a (start_m,stop_m*) pair returned from the HMM algorithm for a single molecule. The z-amplitude of the spike reflects how many such transitions were found for that molecule. Each molecule has slightly different (start_m,stop_m*) pairs so there is no overlap. The task then is to determine some probability landscape that gives rise to the collection of points observed. To do this we use a combination of two-dimensional Gaussians. The number of Gaussians is determined by the number of states we are attempting. Note that the distributions tend to scatter more in a direction parallel to the bottom-left to upper-right (from here on dubbed the positive) diagonal. This is a result of heterogeneous broadening which is discussed later. Because of this asymmetric broadening we employ two-dimensional Gaussians which have orthogonal components het() and hom() defined as follows:

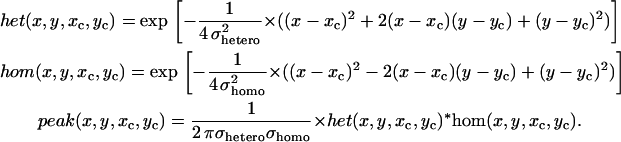(7)

This defines a normalized two-dimensional Gaussian with center (x_c,y_c), positive diagonal width σ_hetero and negative diagonal width σ_homo.

FIGURE 5.

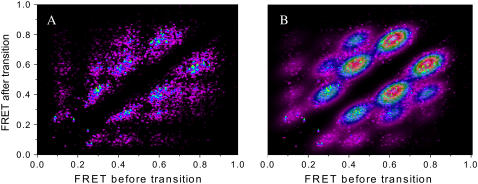
Determining the most likely number of states probabilistically. (A) The data from Fig. 8's TDP are plotted again but with infinitely narrow widths so that each point appears as a spike with amplitude equal to the number of transitions found. By using the BIC (Eq. 10), we find that the most likely number of underlying states for this data set is five. The optimized prob₅(x,y) function is overlaid in B.

If we assume that there are S underlying states, then there must be a total of S × (S − 1) two-dimensional Gaussians. To find the probability of a transition being found at position (x,y) given a series of FRET positions s_i we define a probability function prob_S(x,y):

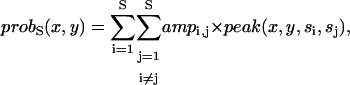(8)

where amp_i,j is a weighting factor for each peak normalized to unity. We already know all the transitions that were found (start_m, stop_m*, a_m,m*), so we simply find the likelihood that our proposed prob_S(x,y) function yields the observed transitions by finding the product of each transition's individual probability.

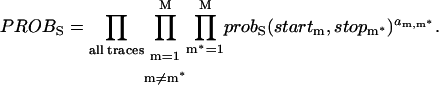(9)

The parameters of our prob_S function are: the s_i (1 ≤ i ≤ S) FRET values of the S different states, the σ_hetero peak width in the positive diagonal direction, the σ_homo peak width in the negative diagonal direction, and amp_i,j (1 ≤ i ≤ S, 1 ≤ j ≤ S, i ≠ j), the normalized peak amplitudes of the S × (S − 1) different peaks. Using Brent's algorithm again we vary these parameters until the prob_S is maximized for different choices of S, the number of underlying states. To determine which S is best we use the Bayesian information criterion (BIC) (22):

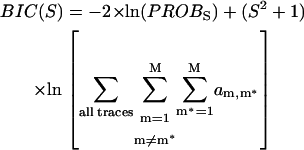(10)

We can then determine BIC(S) for different S values until a minimum is reached; at that point the value that minimizes BIC(S) is the most likely number of underlying FRET states. For the data in Fig. 5 A, such a minimum was reached with the five-state prob₅(x,y) overlaid in Fig. 5 B. With prob_S(x,y) known, one can easily determine which of the underlying (s_i,s_j) peaks each detected (start_m, stop_m*) transition belongs to (if any). Once this list is compiled, each (s_i,s_j) peak's mean transition probability and associated error are determined from Eqs. 4 and 5 above.

ROBUSTNESS OF THE ALGORITHM

To determine the robustness of the algorithm we tested its response to changes in various parameters (Fig. 6). Simulated data were generated by adding Gaussian white noise to a series of idealized donor and acceptor trajectories, while varying the transition probabilities, states' FRET values, or trace length.

FIGURE 6.

Algorithm response to changes in trace parameters with 400 traces. Open squares correspond to systematic error |ln(k/k*)|; solid squares correspond to the probability that FRET states obtained match the true values. Data taken based on 1000 frames/trace (identical to the nearly infinite 40,000 frames/trace) reflect changes in: (A) spacing between FRET states, (B) FRET peak width (δ, or noise), and (C) FRET state lifetime, respectively. (D) The algorithm response with respect to the length of traces. The results suggest that the algorithm will yield a system's true FRET states and transition rates as long as FRET spacing is greater than FRET noise width, data sampling occurs at twice the rate of typical transitions, and at least one transition occurs per trace.

Effect of FRET difference, noise, and data rate

We first considered traces of nearly infinite length (40,000 time steps); adding more time steps did not yield greater precision. The standard parameters were as follows: FRET_A = 0.3 (state A) and FRET_B = 0.7 (state B) with a ΔFRET ≡ |FRET_B − FRET_A| = 0.4, FRET noise width δ of 0.144, a typical value found in real data, and transition probabilities of tp_A→B = 0.05 and tp_B→A = 0.02. Each parameter was varied, whereas the others remained constant so as to determine the impact of that parameter, and 100 traces were analyzed for each choice of parameters.

The success of the algorithm was measured in two ways. First, we determined what fraction of the 100 traces returned the true FRET values (0.3 (±0.05) or 0.7 (±0.05)) (solid squares in Fig. 6). Second, the deduced transition probability k* was compared to the true value k and |ln(k/k*)| plotted (open squares in Fig. 6).

Fig. 6 A shows the effect of changing ΔFRET, the spacing between the two idealized FRET values. The algorithm responds well with <40% error in transition probability and close to 100% yield of returning correct FRET values down to a ΔFRET of 0.1. Fig. 6 B shows the effect of FRET noise, parameterized by δ. The algorithm responds well to increased noise, breaking down only when δ > 0.4. Fig. 6 C shows the effect of data integration time relative to the state lifetimes. Here we vary the transition probabilities tp_A→B and tp_B→A to change their absolute values while preserving their ratio. Since tp_A→B > tp_B→A, we plot the algorithm response against the ratio of the data integration time and the dwell time of state A. Adequate state detection and transition probability determination (11% error) can be made even when the data integration time is only 60% longer than the state dwell time.

Effect of trace length

So far we have considered the cases wherein the observation time window was practically infinite, but in real experiments, the observation time is limited by photobleaching. Fig. 6 D shows the algorithm performance versus the average number of transitions per trace. For the standard transition probabilities used here, ∼100 data points are necessary to determine their values within 20%, which corresponds to only 1.5 transitions per trace on average.

Number of traces needed

Up to this point all discussions of error have related to systematic error, i.e., unavoidable error that could not be reduced by analyzing more traces. We found that even with as few as 20 traces, a number routinely obtained in single molecule experiments, the statistical contribution to error is minimal, at only 8% for the standard parameters (data not shown).

More complex systems

In moving from simple two- to three- or more-state systems, results will follow those described for the three-state system as long as (A), the FRET states are separated by at least the same distance as the noise width of FRET states; (B), the sampling rate is greater than the transition rate for all states; and (C), the system transits between each of the states more than once per trace. Of these criteria, by far the hardest to satisfy as the system becomes more complex is the last one. Since for every state added there are 2 (S − 1) new entries in the transition probability matrix it becomes difficult to obtain traces that show transitions from every state to every other state. Fortunately in many systems not all transitions are possible or some transitions are very rare, allowing one to neglect several entries in the transition probability matrix and significantly reduce the requirements. For example, Fig. 4 shows the transition density plot (TDP) analysis of a simulated five-state data set of 400 traces, 500 data points/trace, FRET noise width of 0.144, and FRET values of 0.18, 0.35, 0.48, 0.63, and 0.78. Transition probabilities ranged from 0.002 to 0.1 and were chosen to favor transitions between neighboring states. The lowest peaks showing a small number of transitions have poor statistics and generate transition probabilities that deviate significantly from the true values. For the 10 highest peaks showing a significant number of transitions, the calculated transition probabilities agreed with the true values within 23%.

Heterogeneous broadening

In real single molecule FRET trajectories different molecules often exhibit different FRET values, even when observed over a sufficiently long time to remove statistical noise. This is particularly noticeable in wide field measurements when looking at trajectories obtained from different image files. This heterogeneous broadening is usually due to instrumental sources such as imperfect alignment of the donor and acceptor detection channels, heterogeneous background on the slide surface, and changes in microscope focusing, and is not necessarily indicative of an underlying molecular heterogeneity. Since this broadening is usually uniform, the result is to shift all FRET values by a nearly constant amount, largely preserving spacing. To test if our algorithm works well even in the presence of heterogeneous broadening, we modified the five-state system described above to exhibit heterogeneous broadening in FRET with a width of 0.15 (typical value obtained experimentally). The resulting TDP is found in Fig. 7. Using the thresholds plotted, the transition rates were calculated, and for the largest 10 peaks (those showing an appreciable number of transitions) the calculated values agreed with the underlying values with a typical error of 15%.

FIGURE 7.

Effect of heterogeneous broadening. The TDP is from exactly the same system as Fig. 2 D, but this time with true FRET state values varying slightly from trace to trace. The width of this distribution was 0.15, a typical value obtained from single-molecule measurements. Despite the smearing, FRET-state values are still discerned and transition rates recovered.

APPLICATION TO EXPERIMENTAL DATA

Holliday junctions

As a first test of the HMM algorithm on real data we studied the well-characterized dynamics of the Holliday junction. In this molecule two adjacent arms of the DNA four-way junction are labeled with a donor and an acceptor and single-molecule FRET time traces are taken as the junction flips between two alternative folded forms (8). Interconversions occurring on the millisecond timescale are detected as transitions between two FRET values. We have compared the idealized trace generated by the HMM algorithm to what we found using the thresholding algorithm as well as the exchange rates deduced using both methods. The HMM output trace fits well with that generated by the thresholding algorithm save for one situation: short-lived transitions. The HMM algorithm allows transitions of one or two time step durations where the thresholding algorithm rarely did, as such transitions were ascribed to noise. Consequently, the HMM algorithm yields transition rates larger than those obtained via the thresholding algorithms (a transition rate of 9 s⁻¹ vs. 6 s⁻¹). Although we cannot judge which one is closer to the true value, we were satisfied that the HMM algorithm returned values comparable to those deduced previously for experimental data.

RecA binding and dissociation

Finally we applied our algorithm to experimental data that could not otherwise be analyzed reliably: the tracking of individual RecA protein binding and dissociation events on a single DNA molecule. Detailed experimental procedures and analysis are published elsewhere (23), but in brief a construct was designed which would exhibit a change in FRET upon binding of a RecA monomer (Fig. 8 A). As more RecA proteins bind the FRET continues to decrease. There was only an initial guess as to the maximum number of RecA monomers that can bind to the DNA, and for that reason the analysis made no assumption about the number of states. Rather, the algorithm was asked to attempt to find a large enough number of states, 10, in the data.

FIGURE 8.

Analysis of a RecA filament data at 250 nM RecA. (A) As more RecA monomers bind, the distance between dyes increases and the FRET efficiency decreases. (B) First raw data (no leakage or cross talk correction) files were analyzed using the modeling algorithm. (C) Next the TDP was generated. Peaks found below 0.2 in either axis are due to acceptor blinking, but the remaining peaks clearly show different binding modes. The highest FRET value (∼0.8 FRET) is bare DNA. Peaks at ∼0.6, ∼0.45, and ∼0.3 indicate one, two, and three RecAs bound, respectively. FRET values are obtained by simply taking the ratio of the acceptor intensity to the sum of the donor and acceptor and should not be used for distance determinations.

Typical data with fit can be seen in Fig. 8 B. The resulting TDP (Fig. 8 C) constructed from raw, uncorrected intensity data shows clearly resolved peaks at 0.15, 0.3, 0.45, 0.6, and 0.8 along each axis. The first, centered at approximately FRET = 0.15 is the result of acceptor blinking, and is not indicative of a true physical state. The remaining four were presumed to be different legitimate FRET states of the system. The 0.8 peak coincides with the value obtained in the absence of RecA and the 0.3 peak coincides with the value obtained with RecA in the presence of ATPγS (where RecA binds stably), leading to the conclusion that the two remaining peaks (0.45 and 0.6) are the result of an intermediate number of RecA molecules bound. Since there are three FRET peaks other than the DNA-only peak indicating that up to three RecA monomers can bind, we label the FRET peaks accordingly (0.8 → M₀, 0.6 → M₁, 0.45 → M₂, and 0.3 → M₃). It is worth noting that the TDP shows transitions occurring primarily between neighboring FRET values, suggesting that RecA binds and dissociates as a monomer. With states defined we proceeded to determine the state-to-state transition rates at various RecA concentrations and graphed the results in Fig. 9. Note that the transition probability of going from M₀ to M₁, thus for binding, increases significantly as higher concentrations of RecA are added (Fig. 9 A). No corresponding change was seen for dissociation for example for the transition probability of going from M₃ to M₂ (Fig. 9 B). We conclude that our algorithm can analyze a complex four-state system without any preconceived model and can return nontrivial conclusions such as transitions being predominantly between nearest neighbors.

FIGURE 9.

RecA binding and dissociating at different concentrations. Histograms are constructed out of the ln(tp) values found in the TDP. (A) We see that as more RecA is added, the likelihood of a bare DNA becoming bound in the next time step (M₀ → M₁) increases significantly. (B) However, the likelihood of a RecA dissociating from a fully bound DNA (M₃ → M₂) construct remains constant. To convert the graphed ln(tp) to an actual transition rate, we exponentiate the mean and multiply by the data acquisition rate (in this case 10 Hz).

SUMMARY

The power of hidden Markov modeling has long been known (24), but until recently had never been applied to single-molecule fluorescence measurements (10,11,14,15), and then only applied to data where individual photon arrival times were known. We have applied modeling to a new and increasingly important set of single-molecule data: FRET trajectories. This enables unambiguous and unbiased separation of noise from state-to-state transitions and reliable analysis of noisy data, and enables examination and detection of significantly more complicated systems, including systems with up to six different states (23), limited only by signal to noise. The molecule-by-molecule nature of the algorithm preserves one's ability to detect heterogeneities in dynamics between molecules which has proven critical in single-molecule studies (7). Potentially the algorithm could also be used to discern states with the same FRET level but with different lifetimes, as with ion channels.

Both the HMM software and the transition density plotting software are publicly available and can be downloaded from our website at http://bio.physics.uiuc.edu/HaMMy.html.