Abstract
Intramolecular interaction networks in proteins are responsible for heterotropic ligand binding cooperativity, a biologically important, widespread phenomenon in nature (e.g., signaling transduction cascades, enzymatic cofactors, enzymatic allosteric activators or inhibitors, gene transcription, or repression). The cooperative binding of two (or more) different ligands to a macromolecule is the underlying principle. To date, heterotropic effects have been studied mainly kinetically in enzymatic systems. Until now, approximate approaches have been employed for studying equilibrium heterotropic ligand binding effects, except in two special cases in which an exact analysis was developed: independent binding (no cooperativity) and competitive binding (maximal negative cooperativity). The exact analysis and methodology for characterizing ligand binding cooperativity interactions in the general case (any degree of cooperativity) using isothermal titration calorimetry are presented in this work. Intramolecular interaction pathways within the allosteric macromolecule can be identified and characterized using this methodology. As an example, the thermodynamic characterization of the binding interaction between ferredoxin-NADP+ reductase and its three substrates, NADP+, ferredoxin, and flavodoxin, as well as the characterization of their binding cooperativity interaction, is presented.
INTRODUCTION
Protein function relies on interaction with other molecules (small organic molecules, proteins, metal ions, nucleic acids, lipids, carbohydrates, etc.), and many proteins interact simultaneously with different ligands. For example, in signaling transduction cascades a first messenger interacts with a cell receptor, which interacts with another protein inside the cell, which becomes activated and interacts with another protein, and so on; some enzymes may need a cofactor, a small noncovalently bound organic molecule, to perform their catalytic function on a substrate; certain proteins and small organic molecules act as activators or inactivators of some enzymes in an allosteric fashion; DNA transcription or repression requires the assembly of multi-macromolecular complexes. The general underlying principle in all these examples is that the binding of a given ligand to a macromolecule influences, favorably or unfavorably, the binding of another ligand to the same macromolecule through an intramolecular network of cooperative short- and long-range interactions distributed throughout the macromolecule, allowing specific local events to have consequences even far from the regions where they take place. Such phenomena may be caused by:
Both ligands binding to the same binding site (competitive binding or maximal negative cooperativity).
Both ligands binding to sites very close to each other, so that the ligands themselves, or certain residues in the macromolecule, constituting or close to the binding sites, may interact.
Both ligands binding to binding sites far apart in the macromolecule, but coupled by a macromolecular conformational change induced by the binding of either ligand and having an effect on the binding of the other ligand (allosterism).
Although it has been often stated that allosteric proteins are oligomeric and symmetric, allosteric proteins can be monomeric, single-domain proteins (1–3), since allostery can be defined in a broad sense as the phenomenon by which the binding of a ligand affects the binding of another ligand (3), and examples have been described in the literature (4–6). This work focuses on the cooperativity interactions in monomeric nonassociating proteins able to bind two different ligands.
Traditionally, heterotropic effects and allosterism have been studied kinetically, with strong emphasis on enzyme regulation, but less attention has been paid to equilibrium experiments and nonenzymatic macromolecules. Moreover, the usual approach is based on an approximate method in which the ternary equilibrium is substituted by an equivalent binary equilibrium and some additional assumptions are made (7–22), as shown in the next section. An exact method has been developed for two special cases only: competitive binding (maximal negative cooperativity) (23,24) and independent binding (no cooperativity, a trivial case).
An exact analysis method developed for determining the equilibrium thermodynamic cooperative parameters (free energy, enthalpy, and entropy) for the cooperative binding of two ligands (with any degree of cooperativity) to a macromolecule using isothermal titration calorimetry is described here. This methodology is useful for characterizing cooperative or interaction networks within protein molecules using isothermal titration calorimetry. Performing point or group mutations in a protein at specific locations, key residues and intramolecular cooperative pathways, responsible for the transmission of information between both binding sites, can be identified and characterized by studying the effect of such mutations on the binding cooperativity parameters.
Although both spectroscopy and isothermal titration calorimetry allow evaluation of the binding affinity (which determines the advance of the reaction because it governs the partition into free and bound species), calorimetry presents a great advantage over spectroscopic techniques: the possibility of determining simultaneously the affinity and the enthalpy of binding. Therefore, it is possible to perform a complete characterization of the binding process (determination of affinity, Gibbs energy, enthalpy, and entropy of binding) in just one experiment. The binding enthalpy is an important parameter in describing the intermolecular driving interactions underlying binding processes, and the mode in which the Gibbs energy of binding is distributed into its enthalpic and entropic components has been proved to have important biochemical and physiological consequences (20,25–30). A detailed description of the technique and its applications, as well as the standard methodology and analysis, can be found elsewhere (31–33).
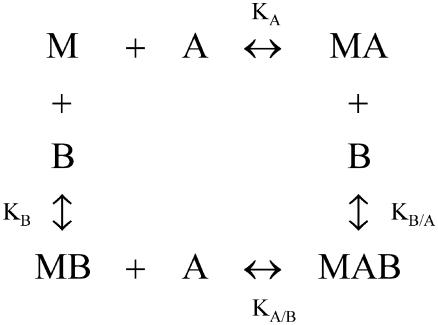
If a macromolecule, M, is able to bind two different ligands, A and B, the formation of the ternary complex, MAB, can be characterized by an interaction or cooperativity constant, α. In general, the binding of one ligand may influence the binding of the other ligand. Fig. 1 shows the general scheme of the ternary equilibrium in which a macromolecule M is able to bind two different ligands (1,2,5,8–10,34–36). KA and KB are the association constants for ligands A and B, respectively, binding to the free macromolecule:
 |
(1) |
and KA/B and KB/A are the association constants for ligands A and B binding to the macromolecule already bound to ligands B and A, respectively:
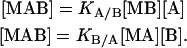 |
(2) |
If the binding of one ligand influences the binding of the other ligand, KA/B and KB/A are different from KA and KB. It follows from Eqs. 1 and 2 that
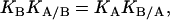 |
(3) |
which is in fact an expression of the energy conservation principle and similar to that of conditional probability (1).
FIGURE 1.
General scheme for the binding of two different ligands, A and B, to a macromolecule, M. In a general scenario, binding of one ligand would influence the binding of the other ligand (heterotropic effect or cooperativity). Therefore, it is necessary to distinguish between the association constants for the binding of either ligand to the free macromolecule, KA and KB, and the association constants for the binding of either ligand to the macromolecule bound to the other ligand, KA/B and KB/A. As explained in the text, the influence of the binding of one ligand on the binding parameters of the other ligand is reciprocal, and it is characterized by the interaction constant α.
If an interaction or cooperativity constant is introduced for the binding of ligand A when ligand B is bound to the macromolecule:
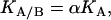 |
(4) |
then, introducing Eq. 4 into Eq. 3, it can be concluded that
 |
(5) |
Therefore, the influence between the two ligands is reciprocal: if the binding of ligand A modifies the binding affinity of ligand B, the binding of ligand B modifies the binding affinity of ligand A in the same extent. The interaction or cooperativity parameter α determines whether the formation of the ternary complex MAB is more or less favorable than in the case of independent binding. If α is equal to zero, the formation of the ternary complex is not possible because the binding of one type of ligand blocks the binding of the other type (maximal negative cooperativity or competitive ligands). If α < 1, the formation of the ternary complex is possible, but the binding of one type of ligand lowers the affinity of binding of the other type of ligand, and the formation of the ternary complex is less favorable than if both ligands bind independently (negative cooperativity or noncompetitive ligands). If α = 1, the formation of the ternary complex is possible and the binding of one type of ligand does not have any influence on the affinity of binding of the other type of ligand (no cooperativity or independent ligands). If α > 1, the formation of the ternary complex is possible and the binding of one type of ligand raises the affinity of binding of the other type of ligand, and the formation of the ternary complex is more favorable than if both ligands bind independently (positive cooperativity or synergistic ligands). By definition, negative values for α are not possible.
The Gibbs energy associated with the formation of each complex is given by:
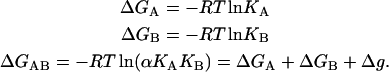 |
(6) |
Then Eq. 3 can be considered a direct consequence of the energy conservation principle or the fact that the Gibbs energy is a state function.
The parameter α is a true equilibrium constant, and it is temperature-dependent (α = α(T)) and related to the interaction or cooperativity Gibbs energy, enthalpy, and entropy:
 |
(7) |
which are obtained by applying the Gibbs-Helmholtz relationship (see Appendix).
If ΔHA and ΔHB are the enthalpies associated with the formation of each binary complex, then the enthalpy associated with the formation of the ternary complex is given by
 |
(8) |
In the same way the conditionally ligand-B-bound association constants were defined (Eqs. 4–5), the enthalpy for ligands A and B binding to the macromolecule bound to ligands B and A, respectively, are given by
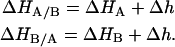 |
(9) |
The parameter Δg represents the additional Gibbs energy (favorable if negative or unfavorable if positive) due to ligand A-ligand B or ligand A-macromolecule cooperative interactions when ligand B is bound to the macromolecule, compared to the Gibbs energy of ligand A binding to the free macromolecule; then, it indicates whether ligand A binds more strongly or more weakly when ligand B is already bound to the macromolecule. In the same way, the parameter Δh represents the additional contribution to the enthalpy (favorable if negative or unfavorable if positive) due to ligand A-ligand B or ligand A-macromolecule cooperative interactions when ligand B is bound to the macromolecule, compared to the enthalpy for ligand A binding to the free macromolecule; then it indicates whether ligand A binds with more favorable enthalpic interactions (e.g., hydrogen bonds, van der Waals, etc.) or less favorable when ligand B is already bound to the macromolecule.
MATERIALS AND METHODS
Purification of ferredoxin-NADP+ reductase and flavodoxin from Anabaena sp. PCC7119
A detailed description of the cloning, expression in Escherichia coli, site-directed mutagenesis, and purification procedures for obtaining Anabaena wild-type ferredoxin-NADP+ reductase (FNRwt), the FNR mutant Y303S (FNRY303S), Fd, and Fld have been published previously (37,38). NADP+ was purchased from Sigma and used without further purification.
High-sensitivity isothermal titration calorimetry
Isothermal titration calorimetry experiments were carried out using a high-precision VP-ITC titration calorimetric system (MicroCal LLC, Northampton, MA). Typically, the FNR solution (∼20 μM) in the calorimetric cell was titrated with NADP+, Fd, or Fld (∼300 μM) dissolved in the same buffer (Tris 50 mM, pH 8.0). In the titration with FNR in the presence of NADP+, the Fd or Fld solution was injected into the calorimetric cell containing a solution of FNR (∼20 μM) and NADP+ (∼50 μM). All solutions were properly degassed and carefully loaded into the cells to avoid bubble formation during stirring. Exhaustive cleaning of the cells was undertaken before each experiment. The heat evolved after each ligand injection was obtained from the integral of the calorimetric signal. The heat due to the binding reaction was obtained as the difference between the heat of reaction and the corresponding heat of dilution, the latter estimated as a constant heat throughout the experiment and included as an adjustable parameter in the analysis.
QUASISIMPLE EQUILIBRIUM: APPROXIMATE ANALYSIS OF THE TERNARY SYSTEM
The ternary equilibrium problem can be addressed through a quasisimple approach, in which the effect of the presence of ligand B on the thermodynamic parameters of the binding of ligand A is accounted for by considering a set of modified apparent thermodynamic parameters dependent on ligand B. From the general scheme shown in Fig. 1, the apparent association constant of ligand A binding to macromolecule M in the presence of ligand B (at a certain concentration) is given by (see Appendix for a detailed derivation)
 |
(10) |
From that expression, the apparent Gibbs energy of binding for ligand A can be evaluated:
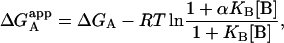 |
(11) |
and also the apparent enthalpy of binding for ligand A:
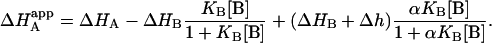 |
(12) |
It is obvious that such apparent binding parameters are not equal to the binding parameters defined in Eqs. 4–9. In particular, the apparent association constant is not equal to the association constant defined by Eq. 4. The origin of the difference is that in Eq. 4 it is assumed that every macromolecule M is bound to ligand B, whereas in Eq. 10, the saturation fraction of macromolecule M with ligand B depends on the binding affinity and the actual concentration of free ligand B. Thus, 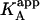 is concentration-dependent, and both
is concentration-dependent, and both 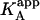 and KA/B coincide in two limit cases: 1), when [B] is zero (trivial situation); and 2), when the product KB[B] is sufficiently high. Therefore, the ratio
and KA/B coincide in two limit cases: 1), when [B] is zero (trivial situation); and 2), when the product KB[B] is sufficiently high. Therefore, the ratio  /KA is not, in general, equal to α. Likewise, the apparent binding enthalpy is not equal to the binding enthalpy defined by Eq. 10. The origin of the difference is the same as that indicated above: in Eq. 9, it is assumed that every macromolecule M is bound to ligand B, whereas in Eq. 12 the saturation fraction of macromolecule M with ligand B depends on the binding affinity and concentration of ligand B. Both
/KA is not, in general, equal to α. Likewise, the apparent binding enthalpy is not equal to the binding enthalpy defined by Eq. 10. The origin of the difference is the same as that indicated above: in Eq. 9, it is assumed that every macromolecule M is bound to ligand B, whereas in Eq. 12 the saturation fraction of macromolecule M with ligand B depends on the binding affinity and concentration of ligand B. Both 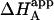 and ΔHA/B coincide in the two limit cases already mentioned: 1), when [B] is zero (trivial situation); and 2), when the product KB[B] is sufficiently high.
and ΔHA/B coincide in the two limit cases already mentioned: 1), when [B] is zero (trivial situation); and 2), when the product KB[B] is sufficiently high.
Therefore, according to the previous equations, the ternary system can be substituted by an equivalent binary system in which there is an implicit influence of ligand B through the apparent thermodynamic parameters for the binding of ligand A. Thus, titrations of the macromolecule with ligand A can be analyzed, in principle, according to the standard procedure for a single ligand binding to a macromolecule. It will be shown later that this will not always be the case.
The reciprocity in the influence of the binding of one ligand on the binding of the other ligand is reflected in the linkage relationships involving the changes in the saturation fraction of each ligand and the changes in the free ligand concentrations (2,39):
 |
(13) |
where FbX is the fraction of macromolecule bound to ligand X (A or B) (see Appendix). These two parameters, γ and ɛ, have the same sign as α − 1. The first one indicates that, if there is positive cooperativity (α − 1 > 0), an increase in ligand B (A) concentration will lead to an increase in the saturation fraction of ligand A (B). Conversely, if there is negative cooperativity (α − 1 < 0), an increase in ligand B (A) concentration will lead to a decrease in the saturation fraction of ligand A (B). If there is no cooperativity at all (α − 1 = 0), an increase in ligand concentration will have no effect on the saturation fraction of the other ligand. The second one indicates that if there is positive cooperativity (α − 1 > 0), an increase in the saturation fraction of ligand B will lead to an increase in the saturation fraction of ligand A, and that an increase in the free concentration of ligand A will cause a decrease in the free concentration of ligand B. Conversely, if there is negative cooperativity (α − 1 < 0), an increase in the saturation fraction of ligand B will lead to a decrease in the saturation fraction of ligand A, and an increase in the free concentration of ligand A will cause an increase in the free concentration of ligand B. If there is no cooperativity at all (α − 1 = 0), an increase in the saturation fraction of ligand B will have no effect on the saturation fraction of ligand A.
It is obvious that the general scheme (Fig. 1) accounts for all possible scenarios: independent and cooperative (competitive, noncompetitive, and synergistic) binding. The traditional methodology applied when studying this type of systems consists of conducting experiments with ligand A binding to the macromolecule in the presence of ligand B in the calorimetric cell. Because the effect of ligand B is included implicitly in the apparent thermodynamic parameters, the binding experiments are analyzed according to the standard procedure for a single ligand binding to a macromolecule. Performing a series of experiments at several concentrations of ligand B, the values for the interaction or cooperativity parameters, α and Δh, can be estimated through nonlinear regression from the dependence of the apparent thermodynamic binding parameters of ligand A, 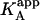 , and
, and 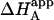 , on the concentration of free ligand B (according to Eqs. 10 and 12) (5,11,13,17–19). It is also possible to perform an experiment at a saturating concentration of ligand B, from which the values of α (and Δh) can be estimated comparing the thermodynamic binding parameters for ligand A binding in the absence and the presence of ligand B (8,9,10,14,20,22,37,40–42). However, as explained above, the apparent affinity for ligand A in the presence of ligand B,
, on the concentration of free ligand B (according to Eqs. 10 and 12) (5,11,13,17–19). It is also possible to perform an experiment at a saturating concentration of ligand B, from which the values of α (and Δh) can be estimated comparing the thermodynamic binding parameters for ligand A binding in the absence and the presence of ligand B (8,9,10,14,20,22,37,40–42). However, as explained above, the apparent affinity for ligand A in the presence of ligand B, 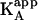 , depends on the free ligand B concentration, the ligand B binding affinity, and the interaction cooperativity constant. Therefore, a saturating concentration of ligand B does not guarantee that the interaction parameters will be accurately estimated. For example, if a titration is simulated, using the exact method explained in the next section, with assumed values of KA = 108 M−1, KB = 106 M−1, [M]T = 20 μM, [A]T = 300 μM, [B]T = 100 μM, and α = 0.01, the value estimated for
, depends on the free ligand B concentration, the ligand B binding affinity, and the interaction cooperativity constant. Therefore, a saturating concentration of ligand B does not guarantee that the interaction parameters will be accurately estimated. For example, if a titration is simulated, using the exact method explained in the next section, with assumed values of KA = 108 M−1, KB = 106 M−1, [M]T = 20 μM, [A]T = 300 μM, [B]T = 100 μM, and α = 0.01, the value estimated for  is of 2.2 × 106 M−1, through nonlinear regression analysis, applying the standard model of a single ligand binding to a macromolecule, and an estimated value of 0.022 would be estimated for the interaction cooperativity constant. This disagreement between the interaction parameters and their estimated values obtained by comparing the thermodynamic parameters in the absence and presence of ligand B, is even more pronounced when α = 0; for example, in that case, as ligand B concentration increases, the apparent binding affinity for ligand A approaches zero, but the zero limit value will never be achieved experimentally.
is of 2.2 × 106 M−1, through nonlinear regression analysis, applying the standard model of a single ligand binding to a macromolecule, and an estimated value of 0.022 would be estimated for the interaction cooperativity constant. This disagreement between the interaction parameters and their estimated values obtained by comparing the thermodynamic parameters in the absence and presence of ligand B, is even more pronounced when α = 0; for example, in that case, as ligand B concentration increases, the apparent binding affinity for ligand A approaches zero, but the zero limit value will never be achieved experimentally.
There are several weaknesses associated with these two approaches:
The concentration of free ligand B is not known accurately in a titration experiment, unless [B]T is much higher than [M]T and the free concentration of B can be approximated by the total concentration of B.
The concentration of free ligand B is not constant throughout the titration experiment, unless the binding of the two ligands is independent (α = 1): if α ≠ 1, then the binding of ligand A promotes the binding or the dissociation of ligand B. Then, the apparent association constant (Eq. 10) and the apparent binding enthalpy (Eq. 12) for ligand A are not constants throughout the titration, and therefore, the analysis of the binding experiments assuming the equivalent binary equilibrium and according to the standard procedure for a single ligand binding to a macromolecule is not accurate and reliable (23).
Because usually the calorimetric experiment is performed at constant cell volume, during the titration experiment the concentration of any molecule in the calorimetric cell decreases as the experiment progresses due to the injection of the titrant solution from the syringe, and therefore, even if the binding of the two ligands is independent (α = 1), the concentration of ligand B is not constant (although one way to avoid this particular problem is adding ligand B in the syringe at the same concentration as in the calorimetric cell; the binding cooperativity still makes the free ligand B concentration nonconstant).
It is assumed in the method that the interaction constant α is the same at any concentration of ligand B, but it might be dependent on the concentration of ligand B (i.e., α = α(T,[B])), and, therefore, the interaction parameter might exhibit different values at low and high concentrations of ligand B (for example, it has been observed that some enzymatic inhibitors may behave as activators, depending on their concentration (43,44); on the other hand, some substrates may act as inhibitors at high concentrations).
It might be impossible to achieve a saturating concentration of ligand B (for example, it may exhibit a very low binding affinity, or it may precipitate or inhibit the macromolecule at high concentrations, or, in the case of maximal or very high negative cooperativity (α equal to zero or very small), high saturating concentrations of ligand B may cause a reduction in affinity so large that the experiment might be rendered useless and nonsaturating concentrations will not provide the right interaction parameters, and then several experiments at low, subsaturating ligand B concentrations must be conducted.
Experiments at fixed nonsaturating concentrations of ligand B may provide more information than experiments at buffered or excess ligand B concentration (35). For all these reasons, in principle, the values of the interaction parameters estimated applying this methodology are approximate and they are characterized by a significant error. It is important to point out that all the previous equations (Eqs. 10–13 and the Appendix equations) are exact. The approximations are introduced when the free ligand concentration to be applied in those equations is estimated and when those equations are applied.
Therefore, to avoid all the problems indicated above, an exact analysis of the ternary equilibrium is required. The exact analysis will present several advantages:
It accounts accurately for the free concentration of ligand B, distinguishing between free and bound ligand, it considers the dilution effect produced along the titration, and it takes into account the possible additional binding or dissociation of ligand B coupled to the binding of ligand A.
The cooperativity interaction parameters are determined under certain specific conditions (e.g., at a particular concentration of ligand B) and it is possible to compare different values of the interaction parameters estimated at different concentrations of ligand B.
The number of experiments required to estimate the interaction parameters is significantly reduced. This last statement is very important from the point of view of saving material and time, because in principle, only three experiments are needed: 1), ligand A binding to the macromolecule, to determine KA and ΔHA; 2), ligand B binding to the macromolecule, to determine KB and ΔHB; and 3), ligand A binding to the macromolecule in the presence of ligand B at a given concentration, to determine α and Δh. Furthermore, the number of experiments may be reduced to only two, because some of the independent binding parameters (KA, KB, ΔHA, and/or ΔHB) can be estimated together with the interaction parameters (α and Δh) in the same experiment if the binding affinity of ligand A is sufficiently high. However, many more experiments are needed in the approximate analysis to cover a reasonable concentration range of ligand B from which the regression analysis for estimating the interaction parameters is possible and accurate. On the other hand, the exact analysis introduces a higher mathematical complexity level, because it requires solving either a system of nonlinear equations or a fifth-order polynomial equation.
To date, the exact analysis of the ternary equilibrium has been developed for two cases only: α = 1 (independent binding or no cooperativity, a trivial situation) and α = 0 (competitive binding or maximal negative cooperativity) (23,24), but not for the general case in which 0 ≤ α < +∞. The exact analysis for the general case (any value of the interaction parameter α) is presented in the next section.
It is important to note that the approximate methodology presented above is the same as the one employed to characterize the pH dependency of ligand binding (45–48). The origin of such dependency is the cooperative coupling between proton binding/dissociation processes and the binding of the ligand. When a ligand binds to a macromolecule, some ionizable groups in the macromolecule or the ligand experience a change in their ionization properties from the free state to the complexed state, in particular a change in the pKa due to an alteration in their microenvironment. The proton affinity is modified in a factor equal to 10ΔpKa and the proton saturation fraction changes according to the change in the pKa and the free proton concentration. Therefore, a proton exchange between the macromolecule-ligand complex and the bulk solution occurs. Depending on the actual change of the pKa values (which determines whether there is a protonation or a deprotonation event) and whether the pH is low or high, the coupled concomitant ligand binding is favored or not. Then, performing titration experiments at different pH values (that is, at different proton concentrations) will provide thermodynamic information on the coupling between the ligand binding and the proton binding (that is, it allows the determination of pKa and ionization enthalpy values for the ionizable groups involved). In this case, the free concentration of protons is known (pH = −log[H+]) and kept constant using an appropriate buffer system, and the previous methodology can be applied with no approximations.
COMPLEX EQUILIBRIUM: EXACT ANALYSIS OF THE TERNARY SYSTEM
From the mass balance for the ternary system, the following set of equations is obtained:
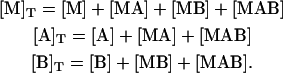 |
(14) |
Introducing Eqs. 1–5, it is converted into a system of three nonlinear equations in three unknowns, the concentrations of free species:
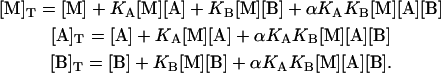 |
(15) |
If α = 0 (maximal negative cooperativity or competitive ligands), solving the system involves solving a cubic equation, which can be accomplished analytically fairly well. However, if α is nonzero and not equal to the unity (no cooperativity or independent binding, a trivial case), it involves solving a quintic equation and two quadratic equations, whose analytical solution is quite complex but can be done numerically. Alternatively, the system of equations can be solved numerically applying the Newton-Raphson method. Once the values of the free concentration of reactants are known, the concentration of the three different complexes, [MA], [MB], and [MAB], can be evaluated applying the mass-action law (Eqs. 1 and 2).
Isothermal titration calorimetry measures the heat associated with a binding process. The instrument performs a series of injections of a ligand solution from a computer-controlled syringe into a macromolecule solution placed in a thermostatized cell, and the heat effect associated with each injection (due to the binding event plus other heat effects related to secondary phenomena that must be subtracted out conveniently) is measured. The concentration of each of the reactants in the calorimetric cell after any injection i is given by
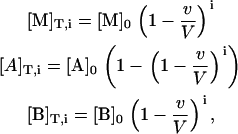 |
(16) |
where [M]0 is the initial concentration of the macromolecule in the calorimetric cell, [A]0 is the concentration of ligand A in the syringe, [B]0 is the initial concentration of ligand B in the calorimetric cell, v is the injection volume, and V is the cell volume. Assuming values for the association constants, KA and KB, and the cooperativity interaction constant, α, it is possible to calculate the concentration of all species in the calorimetric cell after any injection i, solving the set of nonlinear equations (Eq. 15). The heat effect, qi, associated with the injection i can be evaluated as follows:
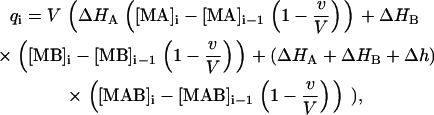 |
(17) |
which indicates that the heat associated with injection i is related to the change in the concentration of each complex after such injection. The thermodynamic binding parameters are estimated from nonlinear least-squares regression analysis of the experimental data using Eq. 17. When the titration does not reach complete saturation or the heat of dilution (the heat effect after saturation due to unspecific phenomena, such as ligand dilution or equilibration between mismatched buffer solutions in syringe and cell) is nonzero it is advisable to include an adjustable parameter qd in Eq. 17 taking into account such effect. Failure to properly estimate the dilution heat will result in inaccurate estimates of the thermodynamic binding parameters.
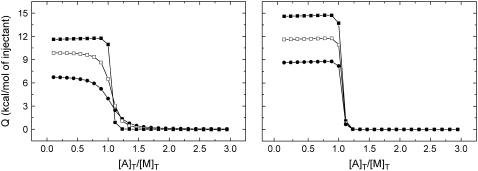
The influence of the cooperative constant on the titration curve is shown in Fig. 2. Three titrations have been simulated with different values of the interaction constant: α = 0.01 (negative cooperativity), 1 (no cooperativity), and 100 (positive cooperativity), which correspond to values of the Gibbs energy of interaction Δg = 2.8, 0, and −2.8 kcal/mol. The cooperativity enthalpy was given a value of 0 kcal/mol to better compare the three situations. Modifying the cooperativity constant affects both the apparent association constant and the apparent binding enthalpy of ligand A. The actual values of these apparent parameters depend on the values of the independent association constants and enthalpies. Choosing appropriately ligand B, it is possible to amplify the signal in the titration experiment. For example, in the case of competitive binding (α = 0), if the weak competitor ligand and the potent displacing ligand have binding enthalpies of opposite sign, the apparent enthalpy (and, therefore, the signal monitored in the calorimeter) will be higher in magnitude than any of the independent enthalpies (29,47–49).
FIGURE 2.
(Left) Influence of the cooperative constant on the titration curve. Three calorimetric titrations with values of the constant α = 0.01 (negative cooperativity, solid circles), 1 (no cooperativity, open squares), and 100 (positive cooperativity, solid squares) have been simulated. The concentration of ligand A in the syringe is 300 μM, and the concentrations of macromolecule and ligand B in the calorimetric cell are 20 μM and 200 μM, respectively. The binding parameters are KA = 107 M−1, ΔHA = 10 kcal/mol, KB = 104 M−1, and ΔHB = 5 kcal/mol. The cooperativity enthalpy Δh was given a value of 0 kcal/mol. (Right) Influence of the cooperative enthalpy on the titration curve. Three calorimetric titrations with values of the enthalpy Δh = 3, 0, and −3 kcal/mol have been simulated. The concentration of ligand A in the syringe is 300 μM, and the concentration of macromolecule and ligand B in the calorimetric cell are 20 μM and 200 μM, respectively. The binding parameters are KA = 107 M−1, ΔHA = 10 kcal/mol, KB = 104 M−1, and ΔHB = 5 kcal/mol. The cooperativity constant α was given a value of 100.
Fig. 2 also illustrates the influence of the cooperative enthalpy on the titration curve. Three titrations have been simulated with different values of the enthalpy: Δh = 3, 0, and −3 kcal/mol. The interaction constant was given a value of 100. Modifying the value of the cooperativity enthalpy only affects the apparent binding enthalpy of ligand A. The actual value depends on the value and signs of the independent association constants and enthalpies. The apparent association constant is not affected by the cooperativity enthalpy.
Titrations at different total concentrations of ligand B have been simulated to examine the influence of the concentration of ligand B present in the calorimetric cell. Calorimetric titrations with positive cooperativity (α = 100 and Δh = −3 kcal/mol) and negative cooperativity (α = 0.01 and Δh = 3 kcal/mol) are shown in Figs. 3 and 4, respectively. In both cases, increasing the concentration of ligand B modulates the apparent association constant and the binding enthalpy of ligand A. The apparent binding parameters of ligand A were estimated by nonlinear regression analysis of each titration, using the standard model with a single ligand A binding to the macromolecule, considering no ligand B to be present, and they are represented as a function of free ligand B concentration (Figs. 3 and 4, inset). Then, the interaction parameters, α and Δh, can be estimated from nonlinear analysis of the dependence of the apparent binding parameters of ligand A on free ligand B concentration (according to Eqs. 10 and 12) according to the methodology based on the approximate analysis, knowing the independent binding parameters (KA, KB, ΔHA, and ΔHB). The free ligand B concentration has been determined in the calculations as the concentration of ligand B at the inflection point of the titration, but this value has no practical utility since it is not known a priori. Fortunately, it has been determined (as judged from the accuracy in the estimation of the interaction parameters) that a reasonably good a priori operational estimate of such concentration is: the difference between the total concentration of ligand B and the concentration of macromolecule in the calorimetric cell at the beginning of the experiment if the concentration of ligand B is higher than the concentration of macromolecule (which is the usual circumstance); the total concentration of ligand B if the concentration of ligand B is lower than the concentration of macromolecule.
FIGURE 3.
Influence of the concentration of ligand B present in the calorimetric cell. Titrations at different total concentrations of ligand B in the case of positive cooperativity have been simulated. The concentration of ligand A in the syringe is 300 μM, and the concentration of macromolecule in the calorimetric cell is 20 μM. The concentrations of ligand B in the calorimetric cell are 0 μM (solid squares), 10 μM (open squares), 20 μM (solid circles), 50 μM (open circles), 100 μM (solid triangles), 200 μM (open triangles), and 500 μM (solid upside-down triangles). The binding parameters are KA = 106 M−1, ΔHA = 10 kcal/mol, KB = 2 × 104 M−1, and ΔHB = 5 kcal/mol. The cooperativity parameters are α = 100 and Δh = −3 kcal/mol. (Inset) Apparent binding parameters for ligand A estimated by nonlinear regression of each titration represented as a function of free ligand B: apparent association constant (solid squares) and apparent binding enthalpy (open squares). The interaction parameters estimated by nonlinear regression analysis according to the approximate method (Eqs. 10 and 12) are α = 106 ± 3 and Δh = −3.3 ± 0.2 kcal/mol. The free ligand B concentration was calculated as the concentration of ligand B at the inflection point of the titration. However, using the total concentration of ligand B or the difference between the total concentration of ligand B and macromolecule at the beginning of the experiment slightly improved the estimations. The interaction parameters estimated by nonlinear regression analysis of only one experiment ([B]T = 200 μM) according to the exact method (Eq. 17) are α = 99.8 ± 0.3 and Δh = −2.99 ± 0.02 kcal/mol.
FIGURE 4.
Influence of the concentration of ligand B present in the calorimetric cell. Titrations at different total concentrations of ligand B in the case of negative cooperativity have been simulated. The concentration of ligand A in the syringe is 300 μM, and the concentration of macromolecule in the calorimetric cell is 20 μM. The concentrations of ligand B in the calorimetric cell are 0 μM (solid squares), 10 μM (open squares), 20 μM (solid circles), 50 μM (open circles), 100 μM (solid triangles), 200 μM (open triangles), and 500 μM (solid upside-down triangles). The binding parameters are KA = 108 M−1, ΔHA = 10 kcal/mol, KB = 105 M−1, and ΔHB = 5 kcal/mol. The cooperativity parameters are α = 0.01 and Δh = 3 kcal/mol. (Inset) Apparent binding parameters for ligand A estimated by nonlinear regression of each titration represented as a function of free ligand B: apparent association constant (solid squares) and apparent binding enthalpy (open squares). Due to interparameter dependency and correlation, both interaction parameters could not be estimated by nonlinear regression analysis according to the approximate method (Eqs. 10 and 12). If α is given a fixed value of 0.01, the estimated value for Δh is 3 ± 2 kcal/mol; if Δh is given a fixed value of 3 kcal/mol, the estimated value for α is 0.011 ± 0.005 kcal/mol. Again, using the total concentration of ligand B or the difference between the total concentration of ligand B and macromolecule at the beginning of the experiment slightly improved the estimations. The interaction parameters estimated by nonlinear regression analysis of only one experiment ([B]T = 200 μM) according to the exact method (Eq. 17) are α = 0.010 ± 0.001 and Δh = 3.01 ± 0.02 kcal/mol.
However, the interaction parameters, α and Δh, can be estimated more accurately by nonlinear regression analysis according to the methodology based on the exact analysis (according to Eq. 17), knowing the independent binding parameters (KA, KB, ΔHA, and ΔHB). Only one titration experiment is required to estimate the interaction parameters, instead of a series of experiments, saving time and material. Moreover, there is no need for estimating a priori the concentration of free ligand B.
Another inconvenience in applying the approximate methodology is that the titrations with ligand A are not symmetrical with respect to the inflection point at low concentrations of ligand B and cannot be reliably and accurately analyzed with the standard procedure for a single ligand binding to a macromolecule. At moderate binding affinity and low ligand B concentration, they show a positive or negative slope, depending on the sign and magnitude of the cooperativity enthalpy and whether there is positive or negative cooperativity, in the region before saturation (Figs. 3 and 4). Before saturation with ligand A is achieved, binding or dissociation of ligand B is promoted as the ligand A saturation fraction increases due to ligand binding cooperativity, and this phenomenon is reflected as an additional contribution to the observed heat in a particular injection. Then, the free concentration of ligand B is not constant throughout the titration, and the apparent association constant and the apparent binding enthalpy for ligand A are not true constants (Eqs. 10 and 12), depending explicitly on the free ligand B concentration and implicitly on the saturation fraction of macromolecule with ligand A (they may vary much more than 100% throughout the titration, depending on the values of the individual and the cooperativity binding parameters, and the initial concentration of ligand B). At high binding affinity and ligand B at subequimolar concentration ([B]T < [M]T), this phenomenon is more pronounced, where even a nonmonotonic titration with a step or a bump can be observed. Fig. 5 shows calorimetric titrations simulated at a low concentration of ligand B ([B]T = 10 μM, [M]T = 20 μM), and with increasing binding affinities of both ligands A and B (keeping constant the ratio between association constants, KA/KB = 100). At moderate affinities a nonsymmetrical titration is observed, whereas at high affinities a well-defined step or bump appears. There is a simple explanation for this fact. At low ligand B concentration, there are two classes of binding sites for ligand A: binding sites in a free macromolecule and binding sites in a ligand-B-bound macromolecule; at the beginning of the titration, the ligand A binds to the binding sites with higher affinity (free macromolecule if there is negative cooperativity, or bound macromolecule if there is positive cooperativity), but as the titration progresses, the ligand A binds to the binding sites with lower affinity (bound macromolecule if there is negative cooperativity or free macromolecule if there is positive cooperativity). The transition between these two regimes is more abrupt at higher binding affinities. It is apparent from the simulations that at low subsaturating concentration of ligand B and low binding affinities the different titration curves are almost indistinguishable; under such conditions, it is more appropriate to employ higher, saturating concentrations of ligand B.
FIGURE 5.
Simulated titrations at low concentrations of ligand B in the calorimetric cell. The concentration of ligand A in the syringe is 300 μM, and the concentrations of macromolecule and ligand B in the calorimetric cell are 20 μM and 10 μM, respectively. The binding enthalpies are ΔHA = 10 kcal/mol and ΔHB = 5 kcal/mol. The cooperativity parameters are α = 0.01 (negative cooperativity (left)), 100 (positive cooperativity (right)), and Δh = 3 kcal/mol. The different titrations have been computed using increasing values of the association constants, but keeping constant the ratio KA/KB: KA = 106 M−1, KB = 104 M−1 (solid squares); KA = 107 M−1, KB = 105 M−1 (open squares); KA = 108 M−1, KB = 106 M−1 (solid circles); KA = 109 M−1, KB = 107 M−1 (open circles); and KA = 1010 M−1, KB = 108 M−1 (solid triangles).
The deviations from the standard titrations at nonsaturating concentrations of ligand B indicate that the approximation of the ternary equilibrium by an equivalent binary equilibrium is not correct, and they should not be considered as artifacts or problematic situations, since they include valuable information on the energetics of the binding cooperativity interactions (35).
HETEROTROPIC EFFECTS IN FERREDOXIN-NADP+ REDUCTASE FROM ANABAENA SP. PCC7119
In plants, algae, and cyanobacteria, Ferredoxin-NADP+ reductase plays a key role during photosynthesis. Thus, its flavin adenine dinucleotide redox cofactor catalyzes the reversible two-electron transfer between two molecules of the one-electron carrier ferredoxin (Fd) and a single NADP+/H molecule, a two-electron carrier. During iron starvation stages, ferredoxin, a protein with an iron-sulfur redox center, is substituted by flavodoxin (Fld), a flavin-mononucleotide (FMN)-dependent protein that in this case acts as a single-electron transfer molecule (50). Kinetic and structural data suggests that the overall process requires the formation of a transient ternary complex between the three partners, FNR, NADP+, and one Fd (or Fld) molecule, in which oxidized FNR is thought to form a complex with NADP+ before its association with reduced Fd (51,52). The direct interaction of NADP+ or Fd (or Fld), that is, the formation of binary complexes, can be characterized performing calorimetric titrations analyzed with the standard model of a single ligand binding to a macromolecule (Table 1). In addition, the interaction cooperativity parameters for NADP+ and Fd (or Fld) binding simultaneously to FNR, that is, the formation of the ternary complex, can be characterized by applying the formalism presented above for characterizing heterotropic interactions (Table 2). To avoid catalysis, the experiments have been performed with the oxidized forms of the molecules involved. Three ternary complexes have been characterized: FNRwt complexed with NADP+ and Fd, FNRwt complexed with NADP+ and Fld, and FNRY303S complexed with NADP+ and Fld. This last mutant FNR shows a much higher affinity for NADP+ than FNRwt, which considerably decreases the steady-state turnover of the enzyme (37), suggesting that this C-terminal Tyr of FNR plays a role in lowering the affinity for NADP+/H to levels compatible with steady-state turnover during catalysis (53).
TABLE 1.
Thermodynamic parameters for binding to FNR
| KA (M−1) | KD (M) | ΔG (kcal/mol) | ΔH (kcal/mol) | ΔS (cal/K·mol) | |
|---|---|---|---|---|---|
| NADP+ → FNRWT | 2.6 ± 0.2 × 105 | 3.8 ± 0.3 × 10−6 | −7.4 ± 0.1 | −0.4 ± 0.2 | 23.3 ± 0.8 |
| NADP+ → FNRY303S | 1.9 ± 0.2 × 108 | 5.2 ± 0.5 × 10−9 | −11.3 ± 0.1 | −8.2 ± 0.2 | 10.5 ± 0.8 |
| Fd → FNRWT | 6.8 ± 0.4 × 105 | 1.5 ± 0.1 × 10−6 | −8.0 ± 0.1 | 7.8 ± 0.2 | 52.7 ± 0.8 |
| Fld → FNRWT | 2.9 ± 0.3 × 105 | 3.5 ± 0.3 × 10−6 | −7.4 ± 0.1 | 5.1 ± 0.2 | 42.0 ± 0.8 |
| Fld → FNRY303S | 1.7 ± 0.2 × 105 | 6.0 ± 0.6 × 10−6 | −7.1 ± 0.1 | 5.4 ± 0.2 | 42.0 ± 0.8 |
TABLE 2.
Thermodynamic parameters for binding to FNR in the presence of NADP+
| α | Δg (kcal/mol) | Δh (kcal/mol) | Δs (cal/K·mol) | |
|---|---|---|---|---|
| Fd → FNRWT + NADP+ | 0.16 ± 0.01 | 1.1 ± 0.1 | 4.5 ± 0.2 | 11.5 ± 0.8 |
| Fld → FNRWT + NADP+ | 0.090 ± 0.006 | 1.4 ± 0.1 | 1.7 ± 0.2 | 1.0 ± 0.8 |
| Fld → FNRY303S + NADP+ | 0.47 ± 0.03 | 0.4 ± 0.1 | −1.8 ± 0.2 | −7.6 ± 0.8 |
FNRwt + NADP+ + Fd
Fig. 6 shows the three titrations required to characterize the ternary complex. From the direct titration of FNRwt with Fd in the absence of NADP+, an association constant of 6.8 × 105 M−1, which corresponds to a dissociation constant of ∼1.5 μM, in agreement with the value of 4 μM reported in the literature (38,50), and a binding enthalpy of 7.8 kcal/mol were estimated by nonlinear regression analysis. Then, the binding of Fd to FNRwt is entropically driven, with an opposing binding enthalpy (see Fig. 9). From the direct titration of FNRwt with NADP+, an association constant of 2.6 × 105 M−1, which corresponds to a dissociation constant of ∼4 μM, in agreement with the value of 5.7 μM reported in the literature (38,50), and a binding enthalpy of −0.4 kcal/mol were estimated by nonlinear regression analysis. Thus, the binding of NADP+ to FNRwt is also entropically driven, with an almost zero binding enthalpy (see Fig. 9). The interaction cooperativity parameters were obtained from the analysis of the titration of FNRwt with Fd in the presence of NADP+. Values of 0.16 and 4.5 kcal/mol were obtained for α and Δh, respectively, from the nonlinear regression analysis of the experiment. Therefore, when any of the two molecules, either Fd or NADP+, is bound to FNRwt, there is a sixfold reduction in the binding affinity of the other molecule (in agreement with the increase in the dissociation constant reported in the literature when Fd is used to titrate FNR in the presence of NADP+ (37)), which corresponds to negative cooperativity with a cooperativity Gibbs energy Δg = 1.1 kcal/mol. This cooperativity interaction energy between Fd and NADP+ bound to FNRwt is the result of a less favorable binding enthalpic contribution (Δh = 4.5 kcal/mol) and a more favorable binding entropic contribution ((−TΔs = −3.4 kcal/mol), as shown in Fig. 9).
FIGURE 6.
Experimental calorimetric titrations for characterizing the ternary complex between FNR, NADP+, and Fd. The experiments were conducted in Tris 50 mM, pH 8.0, at 25°C. In the titration on the left, FNR (20.6 μM in the calorimetric cell) was titrated with Fd (292 μM in the syringe). In the titration in the middle, FNR (20.6 μM in the calorimetric cell) was titrated with NADP+ (300 μM in the syringe). In the titration on the right, FNR (20.6 μM in the calorimetric cell) was titrated with Fd (292 μM in the syringe) in the presence of NADP+ (45 μM in the calorimetric cell). The estimated values from nonlinear analysis are: KFd = 6.8 ± 0.4 × 105 M−1 and ΔHFd = 7.8 ± 0.2 kcal/mol, KNADP+ = 2.6 ± 0.2 × 105 M−1 and ΔHNADP+ = −0.4 ± 0.2 kcal/mol, α = 0.16 ± 0.01, and Δh = 4.5 ± 0.2 kcal/mol.
FIGURE 9.
(A and B) Thermodynamic dissection of the interaction between FNR and each of its substrates: NADP+, Fd, and Fld. The Gibbs energy of binding is represented in blue, the enthalpy of binding in green, and the entropy of binding in red. Any negative value represents a favorable contribution to the binding, whereas a positive value represents an unfavorable contribution to the binding. (C) Thermodynamic dissection of the binding cooperative interaction of NADP+ and Fd or Fld binding to FNR. The cooperative Gibbs energy of binding is represented in blue, the cooperative enthalpy of binding in green, and the cooperative entropy of binding in red. Any negative value represents a favorable additional contribution to the binding, whereas a positive value represents an unfavorable additional contribution to the binding.
FNRwt + NADP+ + Fld
Fig. 7 shows the three titrations required to characterize the ternary complex. From the direct titration of FNRwt with Fld in the absence of NADP+, an association constant of 2.9 × 105 M−1, which corresponds to a dissociation constant of ∼3.5 μM, in agreement with the value of 3 μM reported in the literature (38,50), and a binding enthalpy of 5.1 kcal/mol were estimated by nonlinear regression analysis. Then, as in the case of Fd, the binding of Fld to FNRwt is entropically driven, with an opposing binding enthalpy (see Fig. 9). The interaction cooperativity parameters were obtained from the analysis of the titration of FNRwt with Fld in the presence of NADP+. Values of 0.09 and 1.7 kcal/mol were obtained for α and Δh, respectively, from the nonlinear regression analysis of the experiment. Therefore, when any of the two molecules, either Fld or NADP+, is bound to FNRwt, there is an 11-fold reduction (∼2fold larger than the effect observed with Fd) in the binding affinity of the other molecule (in agreement with the increase in the dissociation constant reported in the literature from 3 μM for the FNR/Fld interaction to 30.6 μM when Fld is used to titrate FNR in the presence of NADP+ (37)), which corresponds to negative cooperativity with a cooperativity Gibbs energy Δg = 1.4 kcal/mol. This cooperativity interaction energy between Fld and NADP+ bound to FNRwt is the result of a less favorable binding enthalpy (1.7 kcal/mol) and a more favorable binding entropy ((−0.3 kcal/mol), as shown in Fig. 9). According to these results, the negative cooperativity effect of NADP+ is higher on the binding of Fld, but the enthalpic and entropic cooperativity contributions are smaller.
FIGURE 7.
Experimental calorimetric titrations for characterizing the ternary complex between FNR, NADP+, and Fld. The experiments were conducted in Tris 50 mM, pH 8.0, at 25°C. In the titration on the left, FNR (20.8 μM in the calorimetric cell) was titrated with Fld (291 μM in the syringe). In the titration in the middle, FNR (20.6 μM in the calorimetric cell) was titrated with NADP+ (300 μM in the syringe). In the titration on the right, FNR (17.5 μM in the calorimetric cell) was titrated with Fld (291 μM in the syringe) in the presence of NADP+ (45 μM in the calorimetric cell). The estimated values from nonlinear analysis are KFld = 2.9 ± 0.3 × 105 M−1 and ΔHFld = 5.1 ± 0.2 kcal/mol, KNADP+ = 2.6 ± 0.2 × 105 M−1 and ΔHNADP+ = −0.4 ± 0.2 kcal/mol, α = 0.090 ± 0.006, and Δh = 1.7 ± 0.2 kcal/mol.
FNRY303S + NADP+ + Fld
Fig. 8 shows the three titrations required to characterize the ternary complex. From the direct titration of FNRY303S with Fld in the absence of NADP+, an association constant of 1.7 × 105 M−1 (which corresponds to a dissociation constant of ∼6 μM) and a binding enthalpy of 5.4 kcal/mol were estimated by nonlinear regression analysis. Then, the binding of Fld to FNRY303S is entropically driven, with an opposing binding enthalpy (Fig. 9). From the direct titration of FNRY303S with NADP+, an association constant of 1.9 × 108 M−1 (which corresponds to a dissociation constant of ∼5 nM, in agreement with the value of <10 nM reported in the literature (53)) and a binding enthalpy of −8.2 kcal/mol were estimated by nonlinear regression analysis. Then, the binding of NADP+ to FNRY303S is enthalpically and entropically driven, but with enthalpy being the the largest contribution (Fig. 9). The interaction cooperativity parameters were obtained from the analysis of the titration of FNRY303S with Fld in the presence of NADP+. Values of 0.47 and −1.8 kcal/mol were obtained for α and Δh, respectively, from the nonlinear regression analysis of the experiment. Therefore, when any of the two molecules, either Fld or NADP+, is bound to FNRY303S, there is only a twofold reduction in the binding affinity of the other molecule (∼5-fold smaller than the effect observed with FNRwt, and in agreement with the increase in the dissociation constant previously reported for the FNR/Fld interaction when Fld is used to titrate FNR in the presence of NADP+ (37)), which corresponds to negative cooperativity with a cooperativity Gibbs energy of ∼0.4 kcal/mol. This cooperativity interaction energy between Fld and NADP+ bound to FNRY303S is the result of a more favorable binding enthalpy (−1.8 kcal/mol) and a less favorable binding entropy (2.2 kcal/mol), as shown in Fig. 9. The mutation Y303S introduced in FNR affects not only the thermodynamic binding parameters associated with single-ligand binding interaction (the NADP+ binding, mainly), but also the thermodynamic parameters associated with the cooperativity binding interactions. These results constitute an example of how binding cooperativity interaction pathways can be modulated and characterized using the methodology presented in this work.
FIGURE 8.
Experimental calorimetric titrations for characterizing the ternary complex between FNR (mutant Y303S), NADP+, and Fld. The experiments were conducted in Tris 50 mM, pH 8.0, at 25°C. In the titration on the left, FNR (20.6 μM in the calorimetric cell) was titrated with Fld (326 μM in the syringe). In the titration in the middle, FNR (20.6 μM in the calorimetric cell) was titrated with NADP+ (283 μM in the syringe). In the titration on the right, FNR (20.6 μM in the calorimetric cell) was titrated with Fld (326 μM in the syringe) in the presence of NADP+ (45 μM in the calorimetric cell). The estimated values from nonlinear analysis are KFld = 1.7 ± 0.2 × 105 M−1 and ΔHFld = 5.4 ± 0.2 kcal/mol, KNADP+ = 1.9 ± 0.2 × 108 M−1 and ΔHNADP+ = −8.2 ± 0.2 kcal/mol, α = 0.47 ± 0.03, and Δh = −1.8 ± 0.2 kcal/mol.
OBSERVED EFFECTS IN VIEW OF STRUCTURAL ARRANGEMENTS OF COMPLEXES
The three-dimensional structures reported for either FNRwt or FNRY303S in complex with NADP+ (52,53) might provide structural information about the above observations. In the case of the mutant, the NADP+ nicotinamide ring is located at the position occupied by Y303 in FNRwt, stacking against the flavin isoalloxazine ring with the adequate stereochemistry for hydride transfer, therefore leaving the overall NADP+ molecule, especially the nicotinamide mononucleotide portion of NAD(P)+/H (NMN) portion, in close interaction with the protein (53), which improves the enthalpic contribution of this interaction. However, in the case of the Anabaena FNRwt, the three-dimensional structure shows a nonproductive complex (52), with the 2′-phospho-AMP portion of NADP+/H and pyrpophosphate portions of the coenzyme perfectly bound, whereas the NMN is placed in a pocket on the protein surface far away from the flavin ring, without making important stacking interactions with the protein (Fig. 10), thus reducing the enthalpic contributions to the enzyme-coenzyme interaction. Comparison of both structures clearly indicates that the NMN portion of the coenzyme interacts much more strongly with the enzyme in the case of FNRY303S mutant than in the case of FNRwt, which is consistent with the larger affinity determined in this work for the mutant, which is mainly driven by the enthalpic contribution as opposed to the interaction of the FNRwt (Table 1).
FIGURE 10.
Putative model for a transient Fld/FNR/NADP+ ternary complex in the cases of Anabaena FNRwt and FNRY303S. This model was obtained by superposition of the FNR coordinates of the putative Fld:FNR complex model (based on the structure of the rat cytochrome P450 reductase (55)) with those in the FNRwt:NADP+ (pdb code 1gjr) (52) and FNRY303S:NADP+ complexes (pdb code 2bsa) (53). Fld is shown in gray balls with its FMN cofactor in black sticks. The FNR surface is shown in light gray and FAD is shown in black. The position of NADP+ for the FNRY303S/NADP+ and the FNRwt/NADP+ complexes' three-dimensional structures are shown in light and dark gray, respectively.
Additionally, since during FNR catalysis the binding of the proteins appears to be ordered for efficient electron transfer, with Fld or Fd binding to a preformed FNR/NADP+ complex, the different orientations of the NADP+ molecule on the complexes with either FNRwt or FNRY303S might produce differences in the interaction parameters upon subsequent binding of the electron carrier protein on either of the preformed enzyme-coenzyme complexes to produce the final productive ternary complex. Thus, it has been shown above that the cooperativity interaction energy between Fld and NADP+ simultaneously bound to FNR presents a much more favorable binding enthalpy and less favorable binding entropy in the case of the FNRY303S than in FNRwt (Fig. 9). Therefore, although the model for the ternary complex (Fig. 10) suggests that the NADP+ binding site on FNR (in both FNRwt and FNRY303S) is not within the protein-protein interface, the most extended conformation of NADP+ in the case of the mutant interaction considerably improves enthalpic contribution to the production of the ternary interaction. This might suggest that, upon coenzyme binding, different structural rearrangements in the loops and side chains around the NADP+ binding site might be produced in ternary complexes involving either FNRwt or FNRY303S.
According to the results presented in this work, the simultaneous binding of NADP+ and Fd or Fld to FNR is characterized by negative cooperativity: the binding of one ligand produces a reduction in the affinity of the other ligand. As explained above, this reciprocal influence can be graphically described making use of the linkage relationship between saturation fractions and free ligand concentrations (Eq. 13), as illustrated in Fig. 11, where the parameter γ (the derivative of the saturation fraction of either ligand with respect to the free concentration of the other ligand) is represented as a function of the free concentration of both ligands. As expected, the larger the cooperativity interaction (in this case, the lower the cooperativity interaction parameter α), the greater the influence, in magnitude and extension, of one ligand over the binding of the other ligand (larger height and base of the peak in the plot). It is interesting to note that the larger the cooperativity effect, the more elliptical and eccentric becomes the peak, and depending on whether there is negative or positive cooperativity, the orientation of the ellipse is from the first to the third quadrant or from the second to the fourth quadrant, respectively.
FIGURE 11.
Linkage relationship between the binding saturation fractions and the free concentration of ligands. The parameter γ (the derivative of the saturation fraction of FNR with a given ligand with respect to the free concentration of ligands NADP+ and Fd or Fld) is plotted as a function of the free concentration of the ligands: (A) ∂Fb,Fd/∂ln[NADP+] or ∂Fb,NADP+/∂ln[Fd] for FNRwt; (B) ∂Fb,Fld/∂ln[NADP+] or ∂Fb,NADP+/∂ln[Fld] for FNRwt; and (C) ∂Fb,Fld/∂ln[NADP+] or ∂Fb,NADP+/∂ln[Fld] for FNRY303S. (D) The parameter ɛ (the derivative of the saturation fraction of FNR with a given ligand with respect to the saturation fraction of the other ligand) is plotted as a function of the free ligand concentration: ∂Fb,Fd/∂Fb,NADP+ for FNRwt (solid line); ∂Fb,Fld/∂Fb,NADP+ for FNRwt (dashed line); and ∂Fb,Fld/∂Fb,NADP+ for FNRY303S (dotted line). Since there is negative cooperativity, γ and ɛ are represented in absolute value (Eq. 13).
The linkage between the binding of two ligands can be described also with a parameter ɛ, which relates the relative change of their saturation fractions (Eq. 13). This parameter is represented as a function of the free ligand concentration in Fig. 11. Contrary to the case of the parameter γ, the parameter ɛ depends only on one free ligand concentration. As expected, the larger the cooperativity interaction (in this case, the lower the cooperativity interaction parameter α), the greater the influence, in magnitude and extension, of one ligand over the binding of the other ligand (larger height and base of the peak in the plot).
Experimental measurements are usually conducted in a solvent containing a buffer to maintain a constant pH and provide an adequate ionic strength. If the binding of two molecules is coupled to the exchange of a number of protons with the bulk solvent, the experimentally observed thermodynamic parameters will contain a contribution associated with the ionization of the buffer (45–48,54). As long as the pH of the experiment is close to the pKa of the buffer employed, the binding affinity and the binding Gibbs energy observed and determined directly from the experiment do not contain any significant contribution from the buffer, and therefore, the observed values do not need any correction. However, the binding enthalpy observed and determined directly in titration calorimetry will be a combination of the intrinsic binding enthalpy and the buffer ionization enthalpy. The intrinsic binding enthalpy can be estimated by performing titrations in the presence of different buffers with different ionization enthalpies and correcting the buffer contribution. As a consequence, the binding entropy needs also to be corrected. All the enthalpy and entropy values presented in this work correspond to observed values that have not been corrected for the influence of the buffer. Therefore, in principle, one should be cautious in making a direct interpretation of the enthalpy and entropy data in terms of the structural features of the complexes formed upon binding. To overcome this problem, titration experiments in the presence of different buffers with different ionization enthalpies would be required. This would be far beyond the scope of the work presented here, which was intended as a demonstration of the methodology, but it will be the objective of a future work. For example, FNR from spinach exhibits a proton exchange process coupled to Fd binding that modifies significantly the observed binding enthalpy depending on the buffer employed: the experimentally determined Fd binding enthalpy in Tris, pH 7.5, is 11 kcal/mol, whereas the corrected intrinsic Fd binding enthalpy is ∼0.3 kcal/mol (54).
CONCLUSIONS
An exact method for characterizing heterotropic ligand binding cooperative effects has been developed. It involves a higher mathematical complexity level compared to the traditional approximate analysis; however, it allows estimation of the binding interaction parameters in only one titration experiment, whereas the approximate analysis requires a set of titration experiments. It has been shown that isothermal titration calorimetry is able to dissect the Gibbs energy associated with single-ligand binding interactions and cooperativity binding interactions into its enthalpic and entropic components. In particular, the binary and ternary complexes formed by FNR and three of its substrates, NADP+, Fd, and Fld, have been characterized thermodynamically. NADP+ might not act as a true allosteric ligand for FNR, because it binds close enough to Fd or Fld to interact directly with them; however, the extension (amount of surface area involved) of the FNR-Fd or FNR-Fld interaction (protein-protein interaction) differs markedly from the FNR-NADP+ interaction (small molecule-protein interaction). The cooperativity interactions characterized in this work correspond to allosteric interactions in the broad sense (i.e., binding of ligand B affects the binding of ligand B). It should be noted that this method does not require knowledge of the three-dimensional structure of any of the interacting molecules.
Structural modifications made on any of the binding partners (via chemical modification or directed mutagenesis) will alter not only the thermodynamic potentials associated with the single-ligand binding interactions, but also the Gibbs energy associated with the cooperativity binding interactions and its partition into its enthalpic and entropic components. In this way, it is possible to dissect the intramolecular interaction pathway responsible for the binding cooperativity interaction by determining the changes in thermodynamic potentials generated by the structural changes.
The exact method allows us to reduce the number of experiments required for an accurate estimation of the interaction binding cooperativity parameters. This is very important considering that ∼1 mg of protein is employed in each calorimetric experiment.
The methodology presented can be used in combination with site-directed mutagenesis for identifying and characterizing interaction pathways responsible for the long-range interaction between binding sites within allosterically regulated proteins.
One of the weak points in the traditional approximate analysis is the problematic estimation of the concentration of free ligand B in a given experiment, due to dilution and association/dissociation phenomena upon binding of ligand A. Although one should follow the exact method in the data analysis, the approximate approach gives a more intuitive description of the dependency of the apparent binding parameters of a given ligand on the binding parameters and concentration of the competitive, noncompetitive, or synergistic ligand.
When applying the approximate approach, the biggest discrepancies in analyzing the dependency of the apparent thermodynamic binding parameters of ligand A,  and
and  , on the concentration of free ligand B occur at low ligand B concentration. These titrations do not agree with the standard model of a single ligand binding to a macromolecule. This is due to the fact that those titrations are not symmetrical with respect to the inflection point, and they show a positive or negative slope in the initial part of the sequence of injections, depending on whether there is positive or negative cooperativity, or even a step at high binding affinities. However, such deviations from the standard model provide information on the binding cooperativity thermodynamics.
, on the concentration of free ligand B occur at low ligand B concentration. These titrations do not agree with the standard model of a single ligand binding to a macromolecule. This is due to the fact that those titrations are not symmetrical with respect to the inflection point, and they show a positive or negative slope in the initial part of the sequence of injections, depending on whether there is positive or negative cooperativity, or even a step at high binding affinities. However, such deviations from the standard model provide information on the binding cooperativity thermodynamics.
It has been shown that the way the cooperativity Gibbs energy is distributed into its enthalpic and entropic contributions gives valuable information about the mode in which the binding of one ligand exerts its influence on the binding of the other ligand and the nature of the structural and energetic features underlying the allosteric phenomenon (8–11,41,42). The use of isothermal titration calorimetry allows the determination of the thermodynamic binding cooperativity parameters (Gibbs energy, enthalpy, and entropy) in a single experiment, without the need to resort to the (usually not very accurate) estimation of the enthalpic contribution from the temperature derivative of the cooperativity interaction constant from a set of experiments (11,41,42). Besides, it is possible, as has been shown in this work with FNR and its substrates, to explore the enthalpy/entropy compensation phenomenon in ternary interactions (8,10).
There are no general rules about the design of a given experiment or about limit values for the binding and cooperativity parameters to detect cooperativity. The effect of ligand B on the binding of ligand A depends on: the binding affinity of ligand B, the concentration of ligand B, the interaction cooperativity constant, the binding enthalpy for ligand B, and the interaction cooperativity enthalpy. For example, if α ≠ 1, cooperativity will be detected even if Δh is close to zero, because the binding affinity for ligand A will be modified by the presence of ligand B (besides, it will always be possible to change slightly the experimental conditions, pH or temperature, to get a nonzero Δh). In principle, in a general interaction scheme (Fig. 1), the ligand B may exhibit a binding affinity lower or higher than the binding affinity of ligand A (as has been illustrated with the experiments shown in this work: NADP+ may bind more weakly or strongly than Fld to FNR). The same applies to the binding enthalpies: there are no limitations in general. However, it can be stated that 1), if the cooperativity is large enough, the signal recorded will be very small if the interaction cooperativity enthalpy and the binding enthalpy for ligand A are of opposite signs and their algebraic sum is <2 kcal/mol (ΔHA + Δh < 2 kcal/mol); 2), the interaction cooperativity constant should be higher than the inverse of the association constant for ligand A (i.e., KAα > 1); otherwise the binding affinity for ligand A in the presence of ligand B might be too low; and 3), if the binding affinity for ligand B is not large enough, high ligand B concentration must be employed to detect cooperativity (that is, the ratio (1 + αKB[B])/(1 + KB[B]) must be significantly different from the unity). There is a special situation in which it is possible to be more precise: if the two ligands are competitive (α = 0), then the binding affinity of ligand B must be at least 10 times lower than the binding affinity of ligand A (otherwise ligand A cannot displace ligand B form the shared binding site), and the binding enthalpy of ligand B must be as different as possible compared to the binding enthalpy of ligand A, if possible of opposite sign, to get an amplified heat effect (if they are equal, the net effect of the displacement is zero).
Errors in reactant concentrations will propagate, causing the estimated binding and cooperativity parameters to have significant errors. As a general rule, the error in ligand A concentration is the most critical (a 10% deviation will cause a 10−15% error in the interaction cooperativity parameters), followed by the error in ligand B concentration (a 10% deviation will cause a 5−10% error in the interaction cooperativity parameters), with the error in macromolecule concentration being much less important (a 10% deviation will cause an error much lower than 5% in the interaction cooperativity parameters). However, it is always possible to minimize the reactant concentration errors (ligands and macromolecule) by performing standard titration experiments in which the binding parameters can be accurately determined and are well known, that is, calibration experiments, similar to active site titrations, in which the reactant active concentrations may be accurately determined from the binding enthalpy estimation (a parameter that depends directly on the syringe reactant concentration) and the binding stoichiometry (a parameter that depends directly on both the syringe reactant concentration and the cell reactant concentration). This is particularly important in proteins, where the concentration determined spectrophotometrically does not always correspond to the concentration of active protein (impurities and partial denaturation are among the usual causes for such discrepancy).
Acknowledgments
A.V.-C. is supported by a grant from the Spanish Ministry of Education and Science SAF2004-07722. M.M. is supported by a grant from the Spanish Ministry of Education and Science BIO2004-00279. A.V.-C. is a recipient of a Ramón y Cajal Research Contract from the Spanish Ministry of Science and Technology. G.G. is a recipient of a fellowship from the Spanish Ministry of Education and Science. J.R.P. is a recipient of a fellowship from the Diputación General de Aragón.
APPENDIX
From the general scheme shown in Fig. 1, the fraction of macromolecule bound to ligand A is given by
 |
(18) |
which can be simplified to a simpler expression if an apparent association constant for the ligand A is defined:
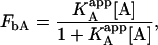 |
(19) |
where
 |
(20) |
This is the apparent association constant that would be obtained if the macromolecule M is titrated with ligand A in the presence of ligand B (at a certain concentration) and the experimental data are analyzed applying a single-ligand binding model. The apparent association constant of ligand A depends on the interaction constant, and the free concentration and the association constant of ligand B. It is a monotonic function of the concentration of ligand B (monotone decreasing for negative cooperativity and monotone increasing for positive cooperativity), having two limit values:
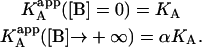 |
(21) |
The apparent Gibbs energy of binding for ligand A can be evaluated as
 |
(22) |
and the apparent enthalpy of binding for ligand A can be evaluated using the Gibbs-Helmholtz relationship:
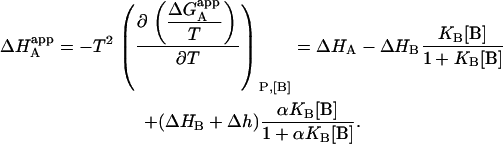 |
(23) |
Similar to the association constant, this is the apparent enthalpy that would be obtained if the macromolecule M is titrated with ligand A in the presence of ligand B (at a certain concentration) and the experimental data are analyzed applying a single-ligand binding model. The apparent binding enthalpy of ligand A depends on the interaction constant, and the free concentration, the association constant, and the binding enthalpy of ligand B. In general, it is not a monotonic function of the concentration of ligand B, exhibiting two limit values:
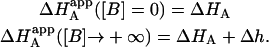 |
(24) |
References
- 1.Weber, G. 1975. Energetics of ligand binding to proteins. Adv. Protein Chem. 29:1–83. [DOI] [PubMed] [Google Scholar]
- 2.Wyman, J., and S. J. Gill. 1990. Binding and Linkage: Functional Chemistry of Biological Macromolecules. University Science Books, Mill Valley, CA.
- 3.Kern, D., and E. R. P. Zuiderweg. 2003. The role of dynamics in allosteric regulation. Curr. Opin. Struct. Biol. 13:748–757. [DOI] [PubMed] [Google Scholar]
- 4.Johnson, L. N. 1994. Control by protein phosphorylation. Nat. Struct. Biol. 1:657–659. [DOI] [PubMed] [Google Scholar]
- 5.Giardina, B., P. Ascenzi, M. E. Clementi, G. De Sanctis, M. Rizzi, and M. Coletta. 1996. Functional modulation by lactate of myoglobin. A monomeric allosteric hemoprotein. J. Biol. Chem. 271:16999–17001. [DOI] [PubMed] [Google Scholar]
- 6.Volkman, B. F., D. Lipson, D. E. Wemmer, and D. Kern. 2001. Two-state allosteric behavior in a single-domain signaling protein. Science. 291:2429–2433. [DOI] [PubMed] [Google Scholar]
- 7.Griffiths, J. R., R. A. Dwek, and G. K. Radda. 1976. Heterotropic interactions of ligands with phosphorylase b. Eur. J. Biochem. 61:243–251. [DOI] [PubMed] [Google Scholar]
- 8.Subramanian, S., D. C. Stickel, A. H. Colen, and H. F. Fisher. 1978. Thermodynamics of heterotropic interactions. The glutamate dehydrogenase-NADPH-glutamate complex. J. Biol. Chem. 253:8369–8374. [PubMed] [Google Scholar]
- 9.Fisher, H. F., S. Subramanian, D. C. Stickel, and A. H. Cohen. 1980. The thermodynamics of a negatively interacting allosteric effector system. J. Biol. Chem. 255:2509–2513. [PubMed] [Google Scholar]
- 10.Fisher, H. F., R. T. Medary, E. J. Wykes, and C. S. Wolfe. 1984. Thermodynamic interactions in the glutamate dehydrogenase-NADPH-oxalylglycine complex. J. Biol. Chem. 259:4105–4110. [PubMed] [Google Scholar]
- 11.Reinhart, G. D., S. B. Hartleip, and M. M. Symcox. 1989. Role of coupling entropy in establishing the nature and magnitude of allosteric response. Proc. Natl. Acad. Sci. USA. 86:4032–4036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Khalifah, R. G., F. Zhang, J. S. Parr, and E. S. Rowe. 1993. Thermodynamics of binding of the CO2-competitive inhibitor imidazole and related compounds to human carbonic anhydrase I: an isothermal titration calorimetry approach to studying weak binding by displacement with strong inhibitors. Biochemistry. 32:3058–3066. [DOI] [PubMed] [Google Scholar]
- 13.Fioretti, E., M. Angeletti, G. Lupidi, and M. Coletta. 1994. Heterotropic modulation of the protease-inhibitor-recognition process. Cations effect the binding properties of α-chymotrypsin. Eur. J. Biochem. 225:450–465. [DOI] [PubMed] [Google Scholar]
- 14.Bradrick, T. D., J. M. Beechem, and E. E. Howell. 1996. Unusual binding stoichiometries and cooperativity are observed during binary and ternary complex formation in the single active pore of R67 dyhydrofolate reductase, a D2 symmetric protein. Biochemistry. 35:11414–11424. [DOI] [PubMed] [Google Scholar]
- 15.Zhang, Y.-L., and Z.-Y. Zhang. 1998. Low-affinity binding determined by titration calorimetry using a high-affinity coupling ligand: a thermodynamic study of ligand binding to protein tyrosine phosphatase 1B. Anal. Biochem. 261:139–148. [DOI] [PubMed] [Google Scholar]
- 16.Bradshaw, J. M., V. Mitaxov, and G. Waksman. 1999. Investigation of phosphotyrosine recognition by the SH2 domain of the Src kinase. J. Mol. Biol. 293:971–985. [DOI] [PubMed] [Google Scholar]
- 17.Edgcomb, S. P., B. M. Baker, and K. P. Murphy. 2000. The energetics of phosphate binding to a protein complex. Protein Sci. 9:927–933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Du, W., W.-S. Liu, D. J. Payne, and M. L. Doyle. 2000. Synergistic inhibitor binding to Streptococus pneumoniae 5-enolpyruvylshikimate-3-phosphate synthase with both monovalent cations and substrate. Biochemistry. 39:10140–10146. [DOI] [PubMed] [Google Scholar]
- 19.De Rosa, M. C., C. Bertonati, B. Giardina, E. Di Stasio, and A. Brancaccio. 2002. The effect of anions on azide binding to myoglobin: an unusual functional modulation. Biochim. Biophys. Acta. 1594:341–352. [DOI] [PubMed] [Google Scholar]
- 20.Protasevich, I. I., C. G. Brouillette, M. E. Snow, S. Dunham, J. R. Rubin, R. Gogliotti, and K. Siegel. 2004. Role of the inhibitor aliphatic chain in the thermodynamics of inhibitor binding to Escherichia coli enoyl-ACP reductase and the Phe203Leu mutant: a proposed mechanism for drug resistance. Biochemistry. 43:13380–13389. [DOI] [PubMed] [Google Scholar]
- 21.Su, Z., M. J. Osborne, P. Xu, X. Xu, Y. Li, and F. Ni. 2005. A bivalent dissectional analysis of the high-affinity interactions between Cdc42 and the Cdc42/Rac interactive binding domains of signaling kinases in Candida albicans. Biochemistry. 44:16461–16474. [DOI] [PubMed] [Google Scholar]
- 22.Jackson, M., S. Chopra, R. D. Smiley, P. O. Maynord, A. Rosowsky, R. E. London, L. Levy, T. I. Kalman, and E. E. Howell. 2005. Calorimetric studies of ligand binding in R67 dihydrofolate reductase. Biochemistry. 44:12420–12433. [DOI] [PubMed] [Google Scholar]
- 23.Sigurskjold, B. W. 2000. Exact analysis of competition ligand binding by displacement isothermal titration calorimetry. Anal. Biochem. 277:260–266. [DOI] [PubMed] [Google Scholar]
- 24.Velazquez-Campoy, A., and E. Freire. 2005. ITC in the post-genomic era…? Priceless. Biophys. Chem. 115:115–124. [DOI] [PubMed] [Google Scholar]
- 25.Myszka, D. G., R. W. Sweet, P. Hensley, M. Brigham-Burke, P. D. Kwong, W. A. Hendrickson, R. Wyatt, J. Sodroski, and M. L. Doyle. 1997. Energetics of the HIVgp120-CD4 binding reaction. Proc. Natl. Acad. Sci. USA. 97:9026–9031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Parker, M. H., E. A. Lunney, D. F. Ortwine, A. G. Pavlovsky, C. Humblet, and C. G. Brouillette. 1999. Analysis of the binding of hydroxamic acid and carboxylic acid inhibitors to the stromelysin-1 (matrix metalloproteinase-3) catalytic domain by isothermal titration calorimetry. Biochemistry. 38:13592–13601. [DOI] [PubMed] [Google Scholar]
- 27.Velazquez-Campoy, A., M. J. Todd, and E. Freire. 2000. HIV-1 protease inhibitors: Enthalpic versus entropic optimization of the binding affinity. Biochemistry. 39:2201–2207. [DOI] [PubMed] [Google Scholar]
- 28.Todd, M. J., I. Luque, A. Velazquez-Campoy, and E. Freire. 2000. Thermodynamic basis of resistance to HIV-1 protease inhibition: calorimetric analysis of the V82F/I84V active site resistant mutant. Biochemistry. 39:11876–11883. [DOI] [PubMed] [Google Scholar]
- 29.Velazquez-Campoy, A., Y. Kiso, and E. Freire. 2001. The binding energetics of first- and second-generation HIV-1 protease inhibitors: implications for drug design. Arch. Biochem. Biophys. 390:169–175. [DOI] [PubMed] [Google Scholar]
- 30.Ward, W. H., and G. A. Holdgate. 2001. Isothermal titration calorimetry in drug discovery. Prog. Med. Chem. 38:309–376. [DOI] [PubMed] [Google Scholar]
- 31.Freire, E., O. L. Mayorga, and M. Straume. 1990. Isothermal titration calorimetry. Anal. Chem. 62:950A–959A. [Google Scholar]
- 32.Velazquez-Campoy, A., and E. Freire. 2003. Isothermal titration calorimetry: measuring intermolecular interactions. In Proteins and Proteomics: A Laboratory Manual. R. Simpson, editor. Cold Spring Harbor Laboratory Press, New York. 882–892.
- 33.Velazquez-Campoy, A., S. A. Leavitt, and E. Freire. 2004. Characterization of protein-protein interactions by isothermal titration calorimetry. Methods Mol. Biol. 261:35–54. [DOI] [PubMed] [Google Scholar]
- 34.Jencks, W. P. 1981. On the attribution and additivity of binding energies. Proc. Natl. Acad. Sci. USA. 78:4046–4050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Robert, C. H., S. J. Gill, and J. Wyman. 1988. Quantitative analysis of linkage in macromolecules when one ligand is present in limited total quantity. Biochemistry. 27:6829–6835. [DOI] [PubMed] [Google Scholar]
- 36.Christopoulos, A., and T. Kenakin. 2002. G protein-coupled receptor allosterism and complexing. Pharmacol. Rev. 54:323–374. [DOI] [PubMed] [Google Scholar]
- 37.Nogues, I., J. Tejero, J. K. Hurley, D. Paladini, S. Frago, G. Tollin, S. G. Mayhew, C. Gomez-Moreno, E. A. Ceccarelli, N. Carrillo, and M. Medina. 2004. Role of the C-terminal tyrosine of ferredoxin-nicotinamide adenine dinucleotide phosphate reductase in the electron transfer processes with its protein partners ferredoxin and flavodoxin. Biochemistry. 43:6127–6137. [DOI] [PubMed] [Google Scholar]
- 38.Medina, M., M. Martínez-Júlvez, J. K. Hurley, G. Tollin, and C. Gómez-Moreno. 1998. Involvement of glutamic acid 301 in the catalytic mechanism of ferredoxin-NADP+ reductase from Anabaena PCC 7119. Biochemistry. 37:2715–2728. [DOI] [PubMed] [Google Scholar]
- 39.Wyman, J. 1964. Linked functions and reciprocal effects in hemoglobin: A second look. Adv. Protein Chem. 19:223–286. [DOI] [PubMed] [Google Scholar]
- 40.Kolb, D. A., and G. Weber. 1975. Quantitative demonstration of the reciprocity of ligand effects in the ternary complex of chiken heart lactate dehydrogenase with nicotinamide adenine dinucleotide and oxalate. Biochemistry. 14:4471–4476. [DOI] [PubMed] [Google Scholar]
- 41.Braxton, B. L., L. S. Mullins, F. M. Raushel, and G. D. Reinhart. 1996. Allosteric effects of carbamoyl phosphate synthetase from Escherichia coli are entropy-driven. Biochemistry. 35:11918–11924. [DOI] [PubMed] [Google Scholar]
- 42.Tlapak-Simmons, V. L., and G. D. Reinhart. 1998. Obfuscation of allosteric structure-function relationships by enthalpy-entropy compensation. Biophys. J. 75:1010–1015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Gerhart, J. C., and A. B. Pardee. 1963. The effect of the feedback inhibitor, CTP, on subunit interactions in aspartate transcarboamylase. Cold Spring Harb. Symp. Quant. Biol. 28:491–496. [Google Scholar]
- 44.Gregory, D. S., and I. B. Wilson. 1971. Studies with aspartate transcarbamylase. Biochemistry. 10:154–161. [DOI] [PubMed] [Google Scholar]
- 45.Baker, B. M., and K. P. Murphy. 1996. Evaluation of linked protonation effects in protein binding reactions using isothermal titration calorimetry. Biophys. J. 71:2049–2055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Xie, D., S. Gulnik, L. Collins, E. Gustchina, L. Suvorov, and J. W. Erickson. 1997. Dissection of the pH dependence of inhibitor binding energetics for an aspartic protease: direct measurement of the protonation states of the catalytic aspartic acid residues. Biochemistry. 36:16166–16172. [DOI] [PubMed] [Google Scholar]
- 47.Velazquez-Campoy, A., I. Luque, M. J. Todd, M. Milutinovich, Y. Kiso, and E. Freire. 2000. Thermodynamic dissection of the binding energetics of KNI-272, a potent HIV-1 protease inhibitor. Protein Sci. 9:1801–1809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Velazquez-Campoy, A., I. Luque, and E. Freire. 2001. The application of thermodynamic methods in drug design. Thermochim. Acta. 380:217–227. [Google Scholar]
- 49.Velazquez-Campoy, A., and E. Freire. 2001. Incorporating target heterogeneity in drug design. J. Cell. Biochem. S37:82–88. [DOI] [PubMed] [Google Scholar]
- 50.Medina, M., and C. Gomez-Moreno. 2004. Interaction of ferredoxin-NADP+ reductase with its substrates: optimal interaction for efficient electron transfer. Photosynth. Res. 79:113–131. [DOI] [PubMed] [Google Scholar]
- 51.Batie, C. J., and H. Kamin. 1984. Electron transfer by ferredoxin:NADP+ reductase. Rapid-reaction evidence for participation of a ternary complex. J. Biol. Chem. 259:11976–11985. [PubMed] [Google Scholar]
- 52.Hermoso, J. A., T. Mayoral, M. Faro, C. Gómez-Moreno, J. Sanz-Aparicio, and M. Medina. 2002. Mechanism of coenzyme recognition and binding revealed by crystal structure analysis of ferredoxin-NADP+ reductase complexed with NADP+. J. Mol. Biol. 319:1133–1142. [DOI] [PubMed] [Google Scholar]
- 53.Tejero, J., I. Pérez-Dorado, C. Maya, M. Martínez-Júlvez, C. Gómez-Moreno, J. A. Hermoso, and M. Medina. 2005. C-terminal tyrosine of ferredoxin-NADPP+P reductase in the hydride transfer processes with NAD(P)P+P/H. Biochemistry. 44:13477–13490. [DOI] [PubMed] [Google Scholar]
- 54.Jelesarov, I., and H. R. Bosshard. 1994. Thermodynamics of ferredoxin binding to ferredoxin:NADP+ reductase and the role of water at the complex interface. Biochemistry. 33:13321–13328. [DOI] [PubMed] [Google Scholar]
- 55.Mayoral, T., M. Martinez-Julvez, I. Perez-Dorado, J. Sanz-Aparicio, C. Gomez-Moreno, M. Medina, and J. A. Hermoso. 2005. Structural analysis of interactions for complex formation between ferredoxin-NADP+ reductase and its protein partners. Proteins. 59:592–602. [DOI] [PubMed] [Google Scholar]