Principles of quasi-equivalence and Euclidean geometry govern the assembly of cubic and dodecahedral cores of pyruvate dehydrogenase complexes

Abstract

The pyruvate dehydrogenase multienzyme complex (M_r of 5–10 million) is assembled around a structural core formed of multiple copies of dihydrolipoyl acetyltransferase (E2p), which exhibits the shape of either a cube or a dodecahedron, depending on the source. The crystal structures of the 60-meric dihydrolipoyl acyltransferase cores of Bacillus stearothermophilus and Enterococcus faecalis pyruvate dehydrogenase complexes were determined and revealed a remarkably hollow dodecahedron with an outer diameter of ≈237 Å, 12 large openings of ≈52 Å diameter across the fivefold axes, and an inner cavity with a diameter of ≈118 Å. Comparison of cubic and dodecahedral E2p assemblies shows that combining the principles of quasi-equivalence formulated by Caspar and Klug [Caspar, D. L. & Klug, A. (1962) Cold Spring Harbor Symp. Quant. Biol. 27, 1–4] with strict Euclidean geometric considerations results in predictions of the major features of the E2p dodecahedron matching the observed features almost exactly.

The large 2-oxo acid dehydrogenase multienzyme complexes catalyze the oxidative decarboxylation of 2-oxo acids (pyruvate, 2-oxoglutarate, and branched-chain 2-oxo acids) to generate the corresponding acyl-CoA and NADH. The pyruvate dehydrogenase (PDH) multienzyme complex is the prototype of this family of proteins and catalyzes a key reaction that generates acetyl-CoA, linking glycolysis to the tricarboxylic acid cycle and the biosynthesis of fatty acids (1).

All 2-oxo acid dehydrogenase complexes share a common architectural design. The core enzyme, dihydrolipoyl acyltransferase (E2), contains either 24 subunits with octahedral 432 symmetry, as found in the PDH complexes of Gram-negative bacteria and all 2-oxoglutarate and branched-chain 2-oxo acid dehydrogenase complexes, or 60 subunits with icosahedral 532 symmetry as seen in the PDH complexes of eukaryotes and Gram-positive bacteria (2). The 2-oxo acid dehydrogenase complexes are unique among proteins in that the E2 component can form a dodecahedron or a cube, depending on the species. In the intact multienzyme complexes, E2 noncovalently binds multiple copies of two peripheral enzymes: the thiamin diphosphate-dependent pyruvate decarboxylase and the flavoenzyme dihydrolipoyl dehydrogenase leading to a M_r of these systems of up to 10 million Da (1). In eukaryotic organisms, additional proteins may be attached to these multienzyme complexes, among them specific kinases and phosphatases involved in metabolic regulation (3) and dihydrolipoyl dehydrogenase-binding proteins.

The dihydrolipoyl acetyltransferase (E2p) of the PDH complex is a dynamic multifunctional multidomain protein (4–7). Each E2p polypeptide chain contains, starting from the N terminus: (i) one to three lipoyl domains of about 80 residues each connected by highly flexible linkers; (ii) one peripheral subunit-binding domain of about 35 residues responsible for binding dihydrolipoyl dehydrogenase and in certain complexes pyruvate decarboxylase; and (iii) a catalytic acetyltransferase domain of approximately 270 residues. The E2p chain of Bacillus stearothermophilus has only one lipoyl domain (8) and that of Enterococcus faecalis has two domains (9, 10), whereas E2p from Azotobacter vinelandii contains three (11). The flexible linkers facilitate the movement of the lipoyl domains such that the lipoyl group attached to a lysine residue in each lipoyl domain can reach the catalytic centers of all three enzymes (12). The catalytic acetyltransferase domains from A. vinelandii E2p form trimers, eight of which assemble into a large hollow cube with a diameter of about 125 Å, “windows” of ≈30 Å across the fourfold axes, and an inner cavity with a diameter of ≈46 Å (13). The reductively acetylated lipoyl group enters the E2p active site channel from the outside of the cube, whereas CoA enters the same active-site channel from the inside of the cube (13–15).

Here we report the crystal structures of dodecahedral cores formed by the catalytic domains of E2p from two Gram-positive bacteria: E. faecalis and B. stearothermophilus, a thermophile. Each has a total molecular mass of about 1.76 million Da. Probably because of the very high solvent content of the crystals and the remarkably hollow architecture of these dodecahedral assemblies, the resolution of the B. stearothermophilus and E. faecalis crystals (16) was limited to 4.4 Å and 4.2 Å, respectively (Table 1). Comparison of the dodecahedral cores reported in this paper with the A. vinelandii cubic core (13) revealed that quasi-equivalent and geometric principles dictate the relationship between these two complex multisubunit arrangements.

Table 1.

Crystallographic data statistics

	B. stearo. E2p	E. faecalis E2p
Space group	F4132	R32
Cell dimensions	a = 534.4 Å	a = 337.8 Å, α = 42.4°
Resolution, Å	4.4	4.2
Completeness	0.634	0.883
Observed/Unique reflections	219,513/34,381	225,561/68,581
Rmerge (last shell)	0.083  (0.387)	0.131  (0.355)

It may be useful to note that “cube” and “dodecahedron” refer to the shape of particles, whereas “octahedral” and “icosahedral” are used, at least in this paper, to indicate the type of symmetry. Hence, 24-meric E2p particles have the approximate shape of a cube with octahedral symmetry and 60-meric E2p particles have the approximate shape of a dodecahedron with icosahedral symmetry.

METHODS

Crystallization and Data Collection for B. stearothermophilus E2p.

Crystals of the catalytic domain E2p of B. stearothermophilus (residues 173–427; ref. 17) were obtained using vapor diffusion by equilibrating 6 μl of a 10 mg/ml of purified protein solution in a 50 mM Tris⋅HCl buffer at pH 8.0 against 6 μl of a reservoir solution containing 20% 2-methyl-2,4-pentanediol (MPD), 100 mM Tris⋅HCl (pH 7.0), and 5% polyethylene glycol (M_r = 1,000). Crystals were cryoprotected by increasing the MPD concentration to 35% while keeping the buffer and additive unchanged.

X-ray data of cryopreserved B. stearothermophilus E2p crystals (at −160°C) were collected on beam line F-1 at the Cornell High Energy Synchrotron Source. Data were recorded on Fuji imaging plates (λ = 0.91 Å) and indexed, integrated, and reduced with denzo and scalepack (18). These crystals belong to space group F4₁32 (a = 534.4 Å) with a pentamer in the asymmetric unit, a solvent content of 89%, and a volume/mass ratio of 11.5 ų/Da. A total of 219,513 observations were merged to 34,381 reflections with an R_merge of 0.083 (Table 1). The data completeness and R_merge in the highest-resolution shell (4.68 Å to 4.4 Å) were 34.9% and 0.387, respectively (Table 1).

Structure Determination of B. stearothermophilus E2p.

The self-rotation function calculated with polarrfn of the CCP4 program suite (18) using the B. stearothermophilus E2p data showed a peak at ω =90°, φ = 31.7°, and κ = 72° with a height of 37% of the origin peak. The orientation of this fivefold axis could be combined with the crystallographic 23-point group symmetry of position (0, 0, 0) to generate all icosahedral symmetry operations of a dodecahedron. The trimer of the cubic A. vinelandii E2p core was assumed to be equivalent to the trimer in the dodecahedral cores (see Results). Therefore, only two global parameters needed to be determined to solve the B. stearothermophilus structure: (i) the distance of the trimer to the origin of the dodecahedron, i.e., the origin of the F4₁32 cell and (ii) the orientation of the A. vinelandii trimer model about the B. stearothermophilus threefold crystallographic axis through (0, 0, 0). The two-parameter R-factor search using data between 15 and 5 Å resulted in a minimum of 0.501 compared with a random-solution R-factor of 0.63. One hundred cycles of fivefold noncrystallographic symmetry averaging with solvent flattening and gradual phase extension from 8 Å to 4.4 Å were performed by using the program dm (19). The final R-factor and correlation coefficient for the phase extension at 4.4-Å resolution were 0.289 and 0.921, respectively. A homology model built on the basis of the A. vinelandii trimer of E2p (13,14) was placed into the averaged electron density by using the program o (20). We refrained from atomic refinement, given the resolution of the data.

Crystallization and Data Collection for E. faecalis E2p.

The E. faecalis E2p crystals were grown as described (16) and belong to space group R32 (a = b = 244.3 Å and c = 920.9 Å, hexagonal setting) with 20 subunits in the asymmetric unit, a solvent content of 73%, and a volume/mass ratio of 4.5 ų/Da. X-ray data were collected at the European Molecular Biology Laboratory–Deutsches Elektronen Synchrotron and merged to 68,581 reflections with an R_merge of 0.131 and 88.3% completeness between 100-Å and 4.2-Å resolution (ref. 16; see Table 1). The E. faecalis E2p crystals diffracted to only about 7 Å initially, but after slow dehydration and rehydration before data collection, the diffraction limit could be improved to 4.2-Å resolution (16).

Structure Determination of E. faecalis E2p.

The self-rotation function as determined with CCP4 polarrfn (18) of E. faecalis E2p indicated the orientation of two fivefold axes in the asymmetric unit at ω = 35°, φ = 90°, κ = 72° and at ω = 80°, φ = 30°, κ = 72°, with peak heights relative to the origin of 55% and 67%, respectively. This orientation corresponds almost exactly to one or more dodecahedra oriented with a threefold axis along the crystallographic threefold axis and one icosahedral dyad parallel to but not coinciding with a crystallographic twofold axis. A peak of 23 σ above the noise level (corresponding to 10% of the origin peak) at position (1/3, 2/3, 1/6) in the Harker section of the native Patterson suggested a translation between two dodecahedra with a similar orientation in the unit cell. Packing considerations allowed the placement of the 20-mer of the B. stearothermophilus search model in the asymmetric unit by centering the dodecahedron at (0, 0, c/4), where the icosahedral threefold axis coincides with the crystallographic threefold axis and the noncrystallographic twofold axes running approximately parallel to the crystallographic twofold axes. Optimizing the orientation of the search model about the crystallographic threefold axis resulted in a solution with the twofold axis ≈5° offset from the crystallographic dyads. The R-factor for this solution was 0.53. One hundred cycles of twentyfold noncrystallographic symmetry averaging with solvent flattening and gradual phase extension from 8 Å to 4.2 Å were performed by using dm (19). The final R-factor and correlation coefficient for the phase extension at 4.2-Å resolution were 0.354 and 0.809, respectively. A homology model was placed into the averaged electron density by using the program o (20). We refrained from atomic refinement because of the limited resolution of the data. Possibly because of the lack of completeness and relatively poor quality of the data (16), the electron density distribution showed weak density for several loop regions at the inner and outer periphery of the dodecahedron. However, the electron density for the trimer–trimer interaction, a key element of this paper, was well determined.

RESULTS

Overall Structure.

For the structure determination, it was assumed that the protomers as well as the trimeric building block of the dodecahedral E2p cores are similar in structure to those described for the cubic PDH core of A. vinelandii E2p (13, 14). This assumption is based on the sequence identities of 38% and 34% between the E2p catalytic domain of A. vinelandii and the corresponding domains of B. stearothermophilus and E. faecalis E2p, respectively. Moreover, the active site of E2p is a long channel at the subunit–subunit interface in the A. vinelandii trimers (13–15), which suggests that the trimer is the conserved basic structural unit in all PDH complexes. The structures of the B. stearothermophilus and E. faecalis E2p cores were obtained by using molecular replacement with 5-fold and 20-fold density averaging, respectively.

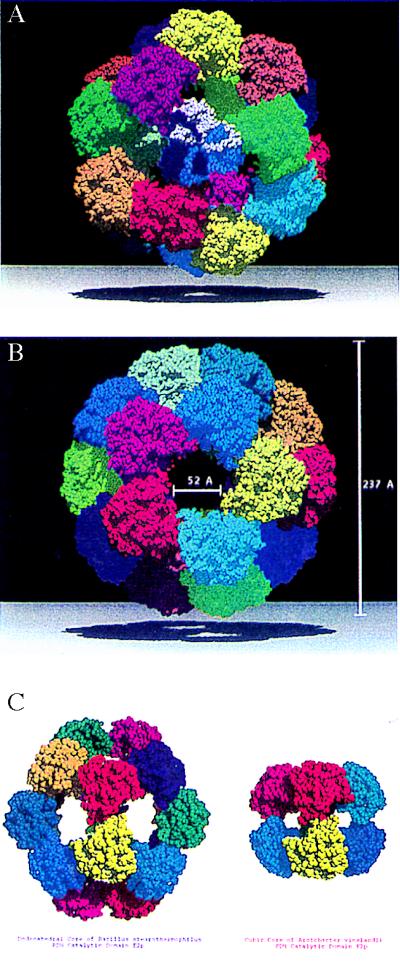
The two crystal structures (Fig. 1) reveal that the maximum outer diameter of the dodecahedral particle is ≈237 Å with a central hollow cavity that has a diameter of about 118 Å. The overall dimensions are in good agreement with those obtained by means of electron microscopy for the dodecahedral E2p cores of B. stearothermophilus (21) and Saccharomyces cerevisae (22). The trimers are packed closely about the threefold axis of symmetry (13, 14) but contact each other only to a limited extent along the icosahedral twofolds, as will be described below. A prominent feature of these dodecahedral cores is the presence of large openings, or “windows,” of ≈52-Å diameter across the fivefold axes (Fig. 1B). In the bacterial PDH complexes, the only function of these openings appears to be that of allowing passage of the substrate (CoA) and the product (acetyl-CoA) between the inner cavity and the solvent surrounding the complex. This is based on the fact that in the corresponding E2p cube of the A. vinelandii PDH complex, access to the CoA-binding site is possible only from the inside of the particle (14, 15). Clearly, the size of these pores is sufficient to allow CoA and acetyl-CoA unhindered entrance into and exit from the interior of bacterial dodecahedral PDH complexes. In the yeast PDH complex, the dodecahedral faces of the E2 core appear to have a function in binding additional proteins (23).

Figure 1.

Space-filling representation (using programs molscript (28) and raster3d (29, 30) of the 60-subunit truncated dodecahedral E2p core of the B. stearothermophilus PDH multienzyme complex. Each of the 20 trimers is colored differently. (A) View along the threefold axis with the central trimer depicted with different colors per protomer. (B) View along the fivefold axis showing the large opening (“windows”) that allow CoA to enter and approach its binding pocket from the internal cavity (14) of the oligomer. The outer diameter of the hollow particle is ≈237 Å, and the solvent-accessible inner space has a diameter of ≈118 Å. (C) View along the twofold axis showing the trimer–trimer subunit interaction and comparison with the cubic E2p core of A. vinelandii (13–15). The height of the cubic core is ≈125 Å and the cross section of the windows is ≈30 Å (13).

The arrangement of proteins with icosahedral symmetry is exceedingly rare for nonviral proteins. To the best of our knowledge, the only other reported nonviral structure with 532 symmetry is riboflavin synthase from B. subtilis (24).

Comparison of Cubic and Dodecahedral E2p Core Structures.

The two dodecahedral E2p core structures can now be compared with the cubic E2p core of A. vinelandii (13, 14) to reveal their differences and relationships in more detail. The key interactions determining the shape and symmetry of the particle are those between the trimeric building blocks across the twofold axes in the cube and dodecahedron. When comparing the intertrimer contacts in cube and dodecahedron, it appears that the C-terminal 3₁₀-helix of one subunit “rotates” in a hydrophobic pocket formed by the other subunit. Even though the averaged electron-density maps of the dodecahedral structures show few indications of side chains, the following general conclusions can be arrived at to explain this difference in oligomeric assembly.

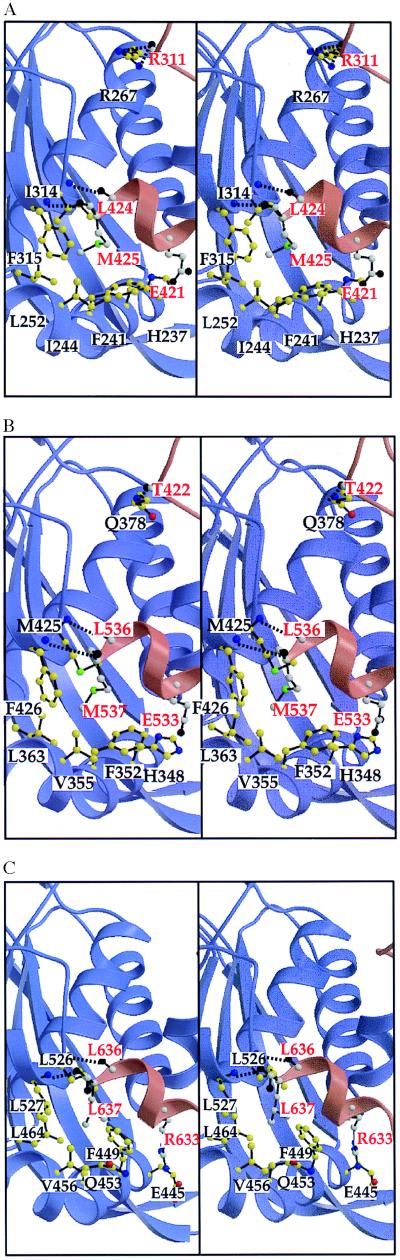
It appears that the different symmetries for each type of E2p core are obtained by a combination of two truly equivalent contacts and several quasi-equivalent interactions. The two truly equivalent contacts are two main-chain–main-chain hydrogen bonds that link the N terminus of helix H4 to the C terminus of the C-terminal 3₁₀ helix of a subunit in the twofold-related trimer (Fig. 2; Table 2).

Figure 2.

Interactions involved in the intertrimer interface of dodecahedral E2p compared with that of the cubic E2p interface. The two protomers involved in the interface are drawn in red and blue, respectively. Residues belonging to the red subunit are labeled in red and colored in black (oxygen), gray (nitrogen), green (sulfur), and white (carbon), whereas residues from the blue subunit are labeled in black and colored in red (oxygen), blue (nitrogen), green (sulfur), and yellow (carbon). Hydrogen bonds are indicated by a dotted line. (A) In the B. stearothermophilus interface, the Met-425 anchor residue of the red subunit interacts with the hydrophobic pocket of the blue subunit lined by residues His-237, Phe-241, Ile-244, Leu-252, Ile-314, and Phe-315. Also, a salt bridge is formed between His-237 (blue subunit) and Glu-421 (red subunit). Hydrogen bonds involving the backbone are formed between residues Ile-314 (blue subunit) and Leu-424 (red), Phe-315 (blue) and Met-425 (red), and Arg-267 (blue) and Arg-311 (red). (B) The E. faecalis E2p trimer–trimer interface is very similar to the one observed in B. stearothermophilus E2p (shown in A). The hydrophobic anchor here is Met-537 (red). The hydrophobic pocket is lined (in blue) by residues His-348, Phe-352, Val-355, Leu-363, Met-425, and Phe-426. (C) In the A. vinelandii E2p interface, the anchor residue Leu-637 (red subunit) interacts with the corresponding hydrophobic pocket lined by residues from the blue subunit Phe-449, Gln-453, Val-456, Leu-464, Leu-526, and Leu-527. The residues involved are equivalent to those in A and B (Table 2; Fig. 3). A salt bridge unique to this octahedral structure is formed by Arg-633 (red) and Glu-445 (blue).

Table 2.

Equivalent and quasi-equivalent intertrimer interactions in dodecahedral and cubic E2p cores of PDH multienzyme complexes

Interactions	Dodecahedral E2p core from B. stearothermophilus	Dodecahedral E2p core from E. faecalis	Cubic E2p core from A. vinelandii (refs. 11 & 12)
Quasi-equivalent
Hydrophobic anchor
	Met-425-r	Met-537-r	Leu-637-r
Residues involved in lining the hydrophobic pocket
	His-237-b	His-348-b	Phe-449-b
	Phe-241-b	Phe-352-b	Gln-453-b
	Ile-244-b	Val-355-b	Val-456-b
	Leu-252-b	Leu-363-b	Leu-464-b
	Ile-314-b	Met-425-b	Leu-526-b
	Phe-315-b	Phe-426-b	Leu-527-b
Equivalent
Backbone hydrogen bond shared among dodecahedral and cubic cores
Donor	Ile-314-b	Met-425-b	Leu-526-b
Acceptor	Leu-424-r	Met-536-r	Leu-636-r
Backbone hydrogen bond shared among dodecahedral and cubic cores
Donor	Phe-315-b	Phe-426-b	Leu-527-b
Acceptor	Met-425-r	Met-537-r	Leu-637-r

The suffix “b” refers to the blue subunits, the suffix “r” to the red subunits in Fig. 2. 

The quasi-equivalent interactions center almost completely on an “anchor” residue that occurs at the end of the C-terminal 3₁₀ helix: Met-425 in B. stearothermophilus E2p, Met-537 in E. faecalis E2p, and Leu-637 in A. vinelandii E2p. The carbonyl oxygen of this anchor residue provides, in fact, one of the hydrogen-bond acceptors of the truly equivalent contact mentioned above. These anchors are sequentially and structurally equivalent in the protomer of both oligomeric assemblies. According to a structure-based alignment of all E2 sequences (A.d.K., A.H.W., T.I., and W.G.J.H., unpublished data), the hydrophobic and aliphatic nature of this anchor residue is conserved among virtually all known sequences of E2s. Only Met and Leu occur at this position, with two exceptions to date: a valine in the protein from Mycoplasma gentalium (MG272 from the Institute for Genomic Research microbial database), and an Ala in Zymomonas mobilis E2p (25). This anchor residue lies in a hydrophobic pocket of the other trimer, which is composed of largely hydrophobic residues in both types of E2p core (Fig. 2, Table 2). In the dodecahedral B. stearothermophilus E2p, the anchor side chain of Met-425 is in contact with three residues of the subunit of a twofold-related trimer (Fig. 2A). In the E. faecalis structure, the Met-537 anchor forms similar contacts with the subunit across the icosahedral twofold (Fig. 2B). The interactions of the anchor residue with the hydrophobic pocket in these dodecahedral complexes are somewhat less extensive than in the cubic A. vinelandii complex, where the Leu-637 anchor side chain is in contact with four residues of the twofold-related subunit (Fig. 2C; ref. 14). Another difference is that Phe-440 in the cubic A. vinelandii structure is much closer to the anchor residue than the equivalent His-237 in the dodecahedral B. stearothermophilus structure (His-348 in E. faecalis). Hence, the interactions between anchor and hydrophobic pocket in the octahedral and icosahedral cores are quasi-equivalent.

We did not succeed in finding a correlation between the amino acid sequences of E2p catalytic subunits and the symmetry they adopt when forming an E2p core. It appears that the final spatial arrangement of trimers is the result of small differences in nature and position of the interface residues.

Construction of the Dodecahedral Core from First Principles.

The principle of quasi-equivalence of Caspar and Klug (26), together with precise Euclidean principles of the geometry of the cube and dodecahedron, allow a surprisingly accurate prediction of the structure of the dodecahedron on the basis of that of the cube. Obviously, the original publication of Caspar and Klug concerned “intraparticle” quasi-equivalence to explain the architecture of virus capsids made up of subunits with identical sequence. This idea is now expanded to “interparticle” quasi-equivalence to explain the relationship between particles made up of subunits with similar but not identical sequence and with different symmetry. The following discussion also describes precisely how to convert a cube built up of 8 trimers into a dodecahedron built of 20 trimers by essentially changing only two parameters. These two parameters (mentioned above in Structure Determination) are the distance R of the trimers from the particle center and the rotation κ about the threefold axes going through the particle center. Euclidean principles govern the angle μ between the threefold axes in the two particles—differing by 28.7°. The principle of quasi-equivalence predicts the two other parameters, R_dodeca and κ_dodeca, starting from R_cube and κ_cube.

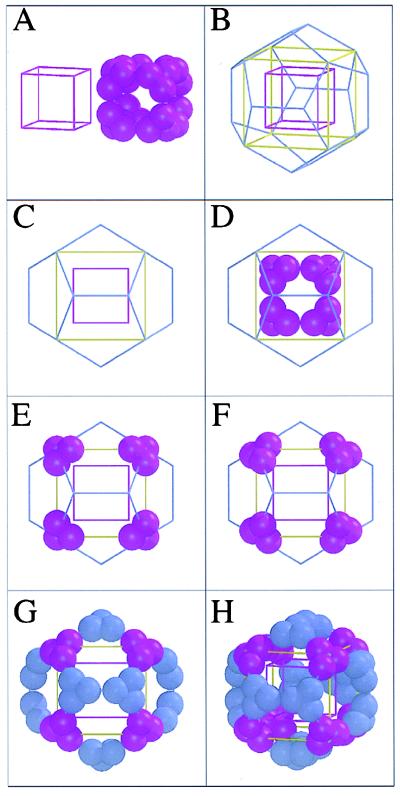
The basis for our discussion lies in Fig. 3 A–D, where a cube is placed inside a dodecahedron such that the threefolds of the cube coincide with a subset of those of the dodecahedron (Fig. 3D). If quasi-equivalent contacts are to govern the relationship between a cube and a dodecahedron made up of similar trimeric building blocks, two conditions must be met. First, the edge of the cube, a_cube, must be similar in length to the edge of the dodecahedron, a_dodeca. Because Euclid (27) had already shown that a_cube = 1/2 √3 R_cube = 1.154 R_cube and a_dodeca = 1/3 (√15 − √3) R_dodeca = 0.714 R_dodeca, it follows from a_dodeca = a_cube that R_dodeca = 1.62 R_cube. Our experimental results provide the distance from the particle center to the C^α of the anchor residue, giving R_cube = 55.3 Å and R_dodeca = 86.3 Å. Hence, R_dodeca = 1.56 R_cube, close to the expected ratio of 1.62 based on the simplified assumption that a_dodeca = a_cube. Actually, as shown in Fig. 4, a more precise derivation leads to a predicted ratio between R_dodeca and R_cube of 1.567, very close to the observed value of 1.561.

Figure 3.

Relationship between cubic and dodecahedral particles constructed from similar trimeric building blocks and with quasi-equivalent contacts across the twofolds. Each sphere represents an E2p subunit. (A) A representation of the A. vinelandii cubic E2p core next to a violet cube C, with edge a_cube and vertex–center distance R_cube, such that the edge runs through the contacts between trimers. (B) Cube C inside a blue dodecahedron D with same length of edge, a, and same particle center. The threefolds of the cube coincide with a subset of the threefolds of the dodecahedron. The yellow cube E is expanded by a factor 1.62 compared with the purple cube C, such that 8 vertices of cube E coincide with 8 of the 20 vertices of the dodecahedron. (C) Cubes C and E, plus the dodecahedron D, viewed along a fourfold axis of the cubes coinciding with a twofold of the dodecahedron. (D) A schematic representation of the 24-meric A. vinelandii E2p cubic core is placed onto cube C. (E) The eight trimers of the original cube C moved outwards by a factor of 1.62 to reside on the vertices of the expanded yellow cube E as well as on the vertices of the dodecahedron D. (F) The eight trimers rotated by 37.7° about the threefold axes such that the quasi-equivalent contact surfaces face each other along a dodecahedral edge instead of a cubic edge (as was the case in Fig. 3E). (G) Twenty trimers generated by applying icosahedral symmetry operations onto one trimer of F. Note that the spheres do not quite touch each other after this operation (see also Fig. 4 B and C). (H) The dodecahedron D, with contacts quasi-equivalent to those in the cube C, shown in the same orientation as in B and decreased slightly in size compared with G such that the spheres touch each other (see also Fig. 4D).

Figure 4.

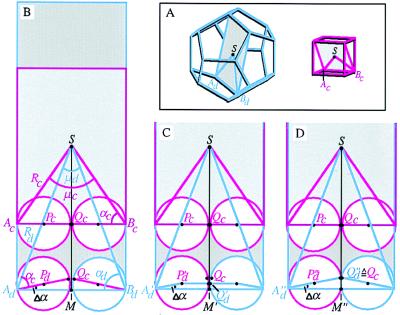
Relationship between cube and dodecahedron with quasi-equivalent contacts along their edges. (A) Left, dodecahedron (blue) with a dark gray plane through two opposite edges and the particle center; Right, cube (violet) with a light gray similar plane through two opposite edges and the particle center. (B) The dodecahedral and cubic planes of A superimposed. The assumption a_cube = a_dodecahedron ( = a) leads to R_dodeca = 1.62 R_cube as derived in the text. As can be seen at the bottom of the figure, this derivation and the requirement that the spatial relationship between the spheres and the threefold axes is the same as the relationship in the cube introduces a small error, and the spheres in the dodecahedron do not make contact. Note that geometric considerations yield μ_d = 41.8°, μ_c = 70.5°, α_c = 54.7°, α_d = 69.1°, and hence Δα = α_d − α_c = 14.4°. (C) Size of dodecahedron when the spherical subunits (with radius 1/4a) touch each other at contact points Q′_d. It is easily seen that now A′_dM′ = (1/4 + 1/4cosΔα) × a. Also, A′_dM′ = A′_dS × sin(1/2μ_d) = R_d × sin(1/2μ_d). This gives R_d × sin(1/2μ_d) = (1/4 + 1/4cosΔα) × a, hence R_d = 1.379a. Because in the cube R_c = 1/2a √3 = 0.866a, we obtain R_d = 1.592R_c, which is a better approximation of the observed relationship R_d = 1.561R_c than obtained in B. (D) E2p subunits are not ideal spheres, and the principle of quasi-equivalence suggests that the contact points Q_c in the middle of the edge A_cB_c of the cube also touch each other in the case of the dodecahedron. In this case, A_d′′M′′ = A′′_dQ′′_d × cosΔα = 1/2a × cosΔα and R_d = A′′M′′/sin(1/2μ_d) = (1/2a cosΔα)/sin (1/2μ_d) = 1.357a. With R_c = 0.866a this yields R_d = 1.567R_c, which is quite close to the observed relationship R_d = 1.561R_c.

The second condition to be met—if principles of quasi-equivalence dictate the relationship between cube and dodecahedron—is that similar contact areas of the trimers must face each other across the twofolds (i.e., along edges) in both particles. After we expand the cube by a factor of 1.62 (Fig. 3E) as required to arrive at the dodecahedron, the trimers that were contacting each other along the edge in the cube (Fig. 3D) must now contact each other along the edge in the dodecahedron. As inspection of Fig. 3 E and F shows, this implies a rotation κ of the trimeric building block about the threefold axis going through the particle center. Geometric considerations show that κ is 37.7°. Experimentally, the observed rotation about the threefold axis is 38.1°, less than 0.5° from the predicted value. In conclusion, Euclidean principles of geometry and the principles of quasi-equivalence derived by Caspar and Klug (26) govern remarkably precisely the relationship between cubic and dodecahedral particles in the pyruvate dehydrogenase complexes.

ABBREVIATIONS

E2

dihydrolipoyl acyltransferase

E2p

dihydrolipoyl acetyltransferase

PDH

pyruvate dehydrogenase