Folding pathway of a lattice model for proteins

Abstract

The folding of a protein-like heteropolymer is studied by using direct simulation of a lattice model that folds rapidly to a well-defined “native” structure. The details of each molecular folding event depend on the random initial conformation as well as the random thermal fluctuations of the polymer. By analyzing the statistical properties of hundreds of folding events, a classical folding “pathway” for such a polymer is found that includes partially folded, on-pathway intermediates that are shown to be metastable equilibrium states of the polymer. These results are discussed in the context of the “classical” and “new” views of folding.

Small proteins typically fold rapidly and reliably to a unique native state from any one of a vast number of initial unfolded conformations. How does this occur? The rapidity of folding, the complexity of protein structure, and the fact that each molecule takes a microscopically different path to the folded state makes this a difficult problem for both experimental approaches (which typically provides ensemble-averaged information with limited temporal and spatial resolution) and all-atom simulations (which can only examine protein motions for nanoseconds rather than the milliseconds needed for folding) (1).

If there are general principles that describe protein folding, then one might expect them to apply to simplified models for protein-like heteropolymers as well. For this reason, models for polymer folding on a lattice have been vigorously pursued (2–9). Although lattice models often omit features that are critical for understanding protein function, they are protein-like in the sense that they fold to a unique native structure from an astronomically large number of possible initial conformations and do so rapidly, reproducibly, and reversibly. The advantages of these models are twofold. First, the thermodynamic driving force for folding is an explicit part of the model, so that the origin of the stabilizing forces can be separated from the problem of folding mechanism. Second, it is straightforward to study a large collection of folding events from start to finish by direct simulation, with complete access to the structural details of every conformation that the polymer samples, without any “dead time.” The challenge is then extracting a useful description of the folding process from the abundance of detail provided by these numerical experiments.

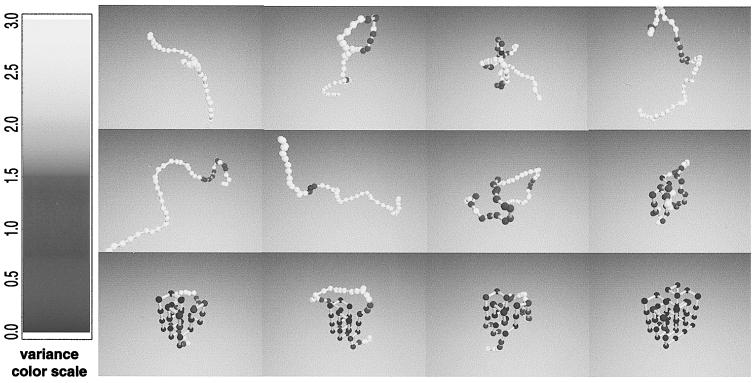
Here we study the folding of a 48-mer on a three-dimensional cubic lattice for which the interresidue interactions have been chosen to stabilize a preselected “native” conformation, shown in the last frame of Fig. 1 (see Methods). This heteropolymer exhibits a cooperative, two-state transition with a midpoint temperature of T_m = 0.74 ± 0.01 (in units of the interaction strength, see Methods) from an unfolded phase U with no persistent structure to a folded phase N consisting of the native conformation and small fluctuations about it. By using Monte Carlo dynamics (see Methods) and a new “fluctuation smear” analysis technique (see below), we examine the sequence of conformations encountered when an initially unfolded polymer is suddenly quenched to a temperature at which the folded state is thermodynamically stable (i.e., below T_m). Each complete simulation—a “folding event”—begins from a different initial unfolded conformation, and proceeds until the native conformation is reached. We follow hundreds of independent folding events and extract their common features—the “folding pathway.”

Figure 1.

Snapshots of a folding event. The average trace of the polymer backbone during the course of a single folding event is shown at intervals of 6 × 10⁴ Monte Carlo steps. The average is taken over a time window of 10⁴ steps. (Whereas the individual conformations lie on the lattice, the average positions need not do so.) The short-time fluctuations of the polymer conformation are encoded by the color of the residue: dark indicates parts of the polymer that are relatively static over the time window (positional variance <  δ r_i  ²> < 0.5), whereas white indicates sections whose position fluctuates strongly (<  δ r_i  ²≫ 3); the fluctuations of residues shaded gray lie in between. A nucleation event (45, 46) is evident at t ≈ 4.9 × 10⁵ steps. The final frame shows the native state conformation.

Our analysis focuses on the nature of the conformations that the polymer samples as it approaches its stable native state. Does structure emerge gradually over the course of the folding event or in relatively rapid, discrete increments? What sets our approach apart from earlier work is our attention to the local and short-time fluctuations of the polymer as it folds (visualized by smear analysis), and the characterization of an ensemble of folding trajectories using hundreds of independent folding events under identical conditions. We find that our model proteins fold via partially folded “on-pathway” intermediates that we characterize statistically.

METHODS

Go Model.

We adopt the Go model (2) for protein-like heteropolymers, which has been widely used for both lattice (10, 11) and off-lattice (12) simulations. In this model, the “energy” of each polymer conformation is taken to be proportional to the number of nearest-neighbor native contacts it possesses, and non-native contacts incur no energetic cost or gain: E(C) = −ɛQ, where ɛ is the energy per native contact and Q is the number of native contacts in conformation C. It is convenient to measure temperature in units of ɛ/R. Note that the energy of a lattice polymer should be thought of as an internal free energy (10) that models the intrapolymer and polymer–solvent interactions as well as the solvent (and effective side chain) entropy for the backbone conformation of interest.

By construction, the native state is the lowest energy conformation of the polymer. The Go model is known to exhibit a large energy gap between native and other unrelated conformations (6) and to fold rapidly to its native state (11). This model embodies the principle of “minimal frustration” (2, 8, 10) in the sense that the driving force for folding is the formation of native contacts, and there are no energetic barriers to achieving the folded state. For this reason the Go model cannot address issues pertaining to misfolded intermediates that are stabilized by non-native contacts. (A Go polymer could, in principle, exhibit an entangled misfolded state, in which some native contacts are formed in a context of a non-native fold. We have not observed this behavior in our simulations.) The fact that misfolded intermediates do not occur in the Go model, however, neither requires nor precludes it from exhibiting on-pathway intermediates, which is the issue we address here.

Native State.

A specific compact conformation on a cubic lattice is selected as the native conformation; the folding events discussed here pertain to the native 48-mer conformation shown in the last frame of Fig. 1. (This structure was originally used in ref. 13.) We have not found any qualitative difference between the nature of the folding pathways for other choices of the native conformation (data not shown). The number of contacts that a given conformation shares with the native state is designated Q ≡ Σ_ijC_ijC_ij^N, where C_ij is the contact map of the conformation: C_ij = 1 if residues i and j are nearest neighbors in space (but not consecutive along the chain) and 0 otherwise. C_ij^N is the contact map of the native state.

Dynamics.

The dynamics of the polymer chain are modeled by a Metropolis Monte Carlo process at temperature T (14). Local movements of the polymer are considered and are always accepted if the new conformation has lower energy but are only accepted with probability exp[−(E_new − E_old)/(R⋅T)] if the energy is increased by the move. Moves include local corner and crankshaft moves as discussed in ref. 5. Monte Carlo dynamics includes both a bias toward lower energies as well as random thermal forces that model energy transfer to and from the solvent, which is assumed to be a heat bath in equilibrium at temperature T. The advantages and potential pitfalls of using such a scheme to model polymer dynamics are reviewed in ref. 15. Simulations are performed on a Cray T3E at the National Energy Research Scientific Computing Center.

Heat Capacity.

From elementary statistical mechanics (16), the heat capacity T∂S/∂T of a system in equilibrium is proportional to its time-averaged energy variance <E²> − <E>². In our model (since energy is proportional to Q), we define c(t) = <Q²> − <Q>². We compute a time-dependent heat capacity c(t) by calculating this variance over conformations sampled within t ± 1.5 × 10⁴ steps. Because in our calculation the energy is actually a potential of mean force, heat capacity peaks reflect the release of polymeric entropy into the environment (i.e., solvent), and are analogous to “latent heat” spikes found at phase transitions.

Folding Probability.

The folding probability (17, 18) p_fold of a given conformation C is determined by a set of additional simulations that are all started from conformation C and allowed to evolve in time. Each simulation is stopped when it reaches either a nearly folded or unfolded conformation. For these purposes, a conformation is deemed folded if Q/Q_max ≥ 90% and unfolded if Q/Q_max ≤ 20%. We typically use 400 runs to determine p_fold, yielding a statistical error of 5%. The folding probability of conformation C is defined as the fraction of these simulations that fold before they unfold. p_fold is highly conformation-dependent. Fig. 1 reports the average p_fold for 500 conformations selected from a time interval of 10⁴ steps.

Free Energy.

The total free energy G(Q, Q_I) is computed by Monte Carlo sampling using a long equilibrium run (10⁹ steps) during which many spontaneous folding and unfolding events occur. Free energy is measured by G(Q, Q_I) = −R T ln Z(Q, Q_I), where Z(Q, Q_I) is the number of conformations sampled in the long Monte Carlo run that have the specified number of native and intermediate contacts. Regions of the (Q, Q_I) plane with low probability can be evaluated by using the standard technique of umbrella sampling (14).

RESULTS

Anatomy of a Folding Event.

Fig. 1 illustrates 12 frames at 6 × 10⁴ time-step intervals from a single folding event at temperature T = 0.65, where each frame represents the average position of each residue during a time window of 10⁴ steps. (A movie of this folding event is available at http://hubbell.berkeley.edu/nsb.html.) The residues are shaded to display the fluctuation in their position during this time interval, as indicated in the caption. The first 8 frames show the polymer in a fluctuating, unfolded state. The 9th, 10th, and 11th frames show persistent partial structure (indicated by the blue structured region). By the final frame, the native state is reached.

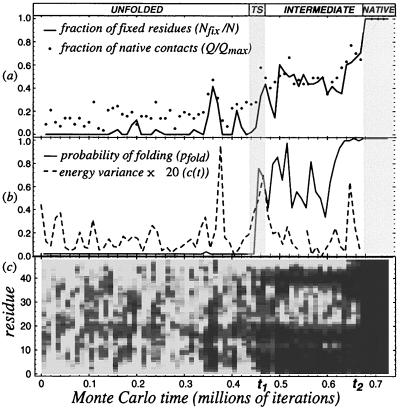
The same folding event is examined in more detail in Fig. 2. Fig. 2c displays the fluctuation in position of the ith residue, using the same color code as in Fig. 1. This fluctuation “smear” (Fig. 2c) clearly exhibits three distinct regimes separated by sharp transitions. The polymer begins in an initial, highly fluctuating unfolded state that persists up to t₁ ≈ 4.9 × 10⁵. It then abruptly switches to a series of conformations with common partial structure, as indicated by the emergence of persistent dark streaks. These conformations possess a specific set of nonfluctuating (“fixed”) residues with high probability. The nature of these contacts is clearly shown in Fig. 1, panels 9–11: the contiguous dark regions along the chain represent a fixed core of contacts—both secondary (i.e., nearby along the chain) and tertiary—whereas the intervening gray region (residues 18–39) represent a fluctuating internal loop.

Figure 2.

Qualitative and quantative probes of a folding event. (a) shows the number of native contacts Q and the number of “fixed” (blue) residues N_fix along the folding trajectory. (b) shows the folding probability p_fold (see Methods) and the energy variance < (δ E)² > of the conformations between t ± 1.5 × 10⁴. (c) shows the positional variance <   δ r_i  ² > vs. time on the horizontal axis and position along the chain on the vertical axis, by using the same shading as in Fig. 1. Note that the static (i.e., dark) residues are clustered in patches for t₁ < t < t₂, representing the persistent core of the intermediate; for t > t₂ all residues become fixed in their native positions, and the polymer is folded.

At time t₂ ≈ 6.8 × 10⁵, there is a rapid transition from the partially folded intermediate state to the completely folded native conformation. This sharp transition corresponds to the rapid absorption of the fluctuating internal loop. At the temperature of the simulation, the unfolding rate from the native state is quite slow, and the polymer remains folded for typically 5 × 10⁷ iterations (data not shown). The fluctuation smear analysis shows that the time evolution of the folding polymer divides into discrete regimes that we characterize below as the unfolded state and metastable intermediates.

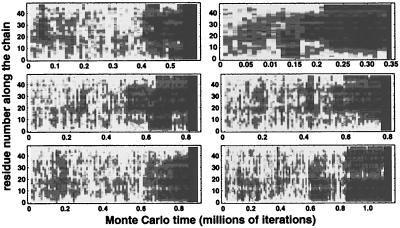
We have studied hundreds of folding events at each of several temperatures, but here we focus on T = 0.65, at which folding typically takes about a million time steps. In these events, the polymer initially remains in the unfolded state for several hundred thousand iterations before undergoing a transition to an intermediate with persistent partial structure. After lingering in an intermediate for a comparable time, the polymer either folds, returns to the unfolded state, or (more rarely) makes a sharp transition to a distinct intermediate regime. The polymer may encounter several intermediate states before finally folding to the native conformation. (Some trajectories also linger in nearly folded conformations with Q/Q_max > 0.9 immediately before complete folding; we regard these conformations as small fluctuations from the native state.) Fig. 3 illustrates this behavior with fluctuation smears for six more folding events at the same temperature as Figs. 1 and 2. This behavior is common to all simulated folding events we studied.

Figure 3.

Fluctuation smears for six different folding events. As in Fig. 2c, we plot the variance of the position of a residue (averaged over an interval of 10⁴ steps) as a function of time for six different simulation runs at T = 0.65 with different initial configurations. Each event encounters one or more intermediate regimes of specific partial structure before folding.

The transitions between the unfolded and intermediate regimes and between the intermediates and the native state are sharp and highly cooperative, as shown in Figs. 2 and 3. Although here we will often refer to a single event in detail, it must be emphasized that our general results derive from the analysis of hundreds of independent folding trajectories. We characterize the folding pathway of our model protein by identifying the unfolded state and intermediate(s) that are sampled by the folding polymer.

The Unfolded State.

Beginning from an initial unfolded conformation, the polymer rapidly reaches a (metastable) thermal equilibrium. During this first regime (t < t₁ in Figs. 1 and 2), the polymer samples conformations with several native contacts (typically Q/Q_max = 0.18 ± 0.09), but these contacts are fluctuating: specific contacts are not preserved from conformation to conformation, because hardly any residues are stationary (N_fix/N ≈ 0), as shown in Fig. 2b. Here, Q(t) is the number of native contacts found in conformations at time t, and N_fix(t) is the number of residues with low positional variance (darkly shaded in the figures) in these conformations. (Q_max = 57 is the number of contacts in the native conformation and N = 48 is the total length of the chain.)

This rapidly interconverting set of conformations with small Q is found in all folding events and defines the unfolded phase of the polymer. Because below T_m, the thermodynamically stable state of the polymer is the native state, this unfolded state must be regarded as a metastable or supercooled phase. The existence of flickering native contacts in the unfolded state of our protein-like heteropolymer is consistent with the observations of transient structures in the unfolded states of proteins (19–21).

Partially Folded Intermediates.

In Fig. 2, near time t₁, persistent contacts suddenly form, and N_fix/N rises rapidly to become comparable to Q/Q_max. There is only a gradual increase in Q/Q_max at this time. During the interval t₁ < t < t₂, both of these measures of folding progress remain nearly constant. Similar intervals of persistent partial structure appear in all folding events we have examined (see, e.g., Fig. 3). These sharply defined intermediate regimes define collections of rapidly interconverting conformations that comprise the intermediate phases of the polymer. These kinetic intermediates are transient, and do not accumulate. Note that the presence of kinetic intermediates is consistent with a cooperative equilibrium two-state transition in the sense that only the unfolded and native states are ever appreciably populated in equilibrium.

We find that the intermediate regimes found in the folding events we studied can be classified into four distinct classes, each with its own well defined, persistent partial structure. It is not uncommon for the polymer to encounter several intermediates in a single folding event. When this occurs, the intermediates are typically separated by a return to the unfolded state (see Fig. 3). We also occasionally observe rare direct transitions between intermediates that involve either the formation or dissolution of a discrete unit of partial structure. Because we have never seen direct U → N transitions (in 50 events), we conclude that for this system, folding must proceed through an intermediate. Because folding can proceed directly from an intermediate to the native state (as shown, e.g., in Fig. 3), these intermediates (local free-energy minima, see below) are therefore “on-pathway.”

The sudden, discrete changes in the character of the conformational fluctuations of the polymer found in all folding events (e.g., at t₁ and t₂ in Fig. 2) are naturally interpreted as highly cooperative transitions involving metastable phases. Clear peaks in the time-dependent heat capacity c(t) (see Methods) are seen at both boundaries (i.e., t₁ and t₂) in Fig. 2b, indicating sudden releases of heat from the polymer to the thermal bath that reflect the latent heats released at cooperative transitions. (The large c(t) peak seen at t ≈ 3.5 × 10⁵ steps corresponds to the brief formation of a partially folded structure that quickly dissolved, which appears as a short dark patch in Fig. 2c.)

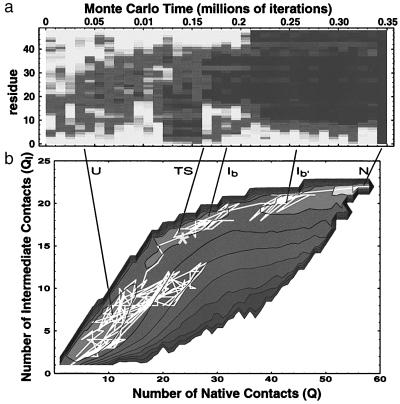
Further evidence that the unfolded and partially folded regimes can be identified with metastable phases is provided by equilibrium Monte Carlo umbrella sampling (see Methods) of the free energy F(Q, Q_I; T), i.e., the free energy as a function of the number of native contacts, Q, and the number of contacts Q_I that are found in common with a representative intermediate conformation. Fig. 4b exhibits three distinct local free-energy minima (corresponding to the unfolded, intermediate, and native phases) with barriers between them. Their relative stability depends on temperature; for T < T_m, the native state has lowest free energy. (The local free-energy minima corresponding to the other intermediates are not visible with this choice of thermodynamic coordinates.) The intermediate states for this polymer are never global free-energy minima because either the unfolded and/or native states are always lower in free energy at all temperatures. This is consistent with the observed two-state nature of the equilibrium transition.

Figure 4.

Kinetic intermediates and free-energy minima. (a) Fluctuation smear. (b) Contours of the free-energy surface G(Q, Q_I-b) projected onto the (Q, Q_I-b) plane are shown superimposed on the trajectory of the folding event shown in a. The free-energy surface was computed by using umbrella sampling during a long equilibrium run (see Methods); Q_I-b Σ_ij⋅C_ij⋅C_ij^I−b is the number of contacts a conformation shares with a representative conformation C_ij^I−b chosen from the intermediate of a. The three distinct free-energy minima correspond to the unfolded, intermediate, and native states; the native state is the most stable of the three; a later intermediate is also evident. [The free-energy minima corresponding to the other metastable intermediates are not visible in this projection onto the (Q, Q_I−b) plane.] The trajectory shows that the polymer fluctuates in the unfolded state before rapidly jumping to the intermediate; from the intermediate complete folding proceeds relatively rapidly.

DISCUSSION

Determining the Transition State Ensemble.

Each folding event samples a different microscopic series of conformations on its way to the final folded state. The transition state for folding is therefore an ensemble of conformations and must be characterized statistically (22). Here we implement a computational method (17, 18) that appeals to the defining characteristic of a transition state as an unstable species that is equally likely to evolve to the product or reactant states (i.e., to fold or unfold). To measure the progress of the reaction, we calculate the folding probability p_fold(C) (18), the probability that a new simulation that starts from conformation C reaches the native state without first unfolding (see Methods). In a reaction without intermediates, the transition state lies at p_fold = 1/2; for more complex reactions, p_fold ≈1/2 determines the dominant transition state. (Note that conformations with p_fold = 1/2 may be encountered several times in a given event.) The folding probability method permits the determination of the transition state without requiring any assumptions regarding the nature of the reaction coordinate or free-energy surface.

Fig. 2b shows the folding probability as a function of time for the folding event shown in Fig. 1. Throughout the initial unfolded regime, p_fold remains zero. A rapid increase in p_fold through 1/2 coincides with the transition between the unfolded and intermediate regimes, when partial, native-like structure first appears. This is shown more dramatically in Fig. 4b, which exhibits a folding trajectory superimposed on the calculated free-energy surface in the (Q, Q_I) plane, where Q_I measures the number of contacts in common with a representative intermediate conformation. (The fluctuation smear for this event is shown in Fig. 4a.) The conformation at which p_fold first exceeds 1/2 is indicated by an asterisk. The transition state as calculated by p_fold does not coincide precisely with the barrier between U and I because Q and Q_I are only approximate reaction coordinates.

We find no apparent precursor to the abrupt increase in p_fold in any of the diagnostic quantities we have measured on time scales on the order of 10⁴ steps, indicating that the change occurs rapidly, i.e., over the course of a few hundred conformations, and does not occur by a gradual accumulation of native structure. Similar abrupt behavior occurs in every folding run we examined.

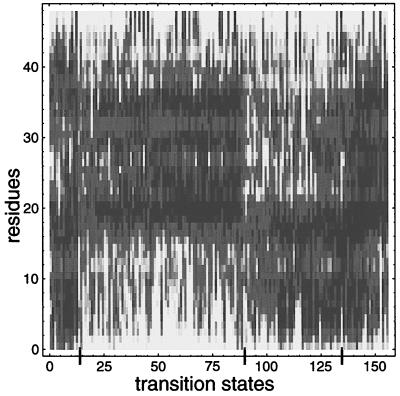
The transition state ensemble can be constructed operationally by collecting the conformations at which p_fold first enters the range 0.4 < p_fold < 0.6 from many independent folding events. Fig. 5 displays the positional variance of the transition states of 156 independent folding events at T = 0.65 with the same color coding as used earlier. [In 134 other events, p_fold jumps from below 0.4 to above 0.6 faster than our p_fold sampling interval of 10⁴ steps; the first conformations encountered with p_fold > 0.6 in these runs are similar to those shown in Fig. 5 (data not shown).]

Figure 5.

Characterization of the transition-state ensemble. The variances of transition-state conformations from 156 independent folding runs at T = 0.65 are displayed by using the shading scheme of Fig. 1. Conformations have been sorted to exhibit the natural partitioning of these conformations into distinct transition state classes. Superimposed on the common structure within each class are various optional structures; these contribute to the entropy of the transition state. As the transition state is structurally similar to the intermediate (see Fig. 4), Fig. 5 also describes the nature of the intermediates found in this system.

Kinetic Intermediates and Metastable States.

Many single-domain proteins, including apomyoglobin (23, 24), barnase (25), interleukin 1β (26), and B1 domain of protein G (27), fold via one or more kinetic intermediates that can sometimes be stabilized under acid or denaturing conditions as equilibrium states. These intermediates appear to possess partial native structure; for example, in the acid state of apomyoglobin, the AGH-helices form a structured region (24). Some recent theories of protein folding, however, have emphasized the role of misfolded intermediates that impede folding by trapping the protein in a locally non-native structure (8, 10, 28, 29). This scenario is consistent with the fact that some small proteins, such as chymotrypsin inhibitor II (30), λ repressor (31), and the cold shock protein Csp (32), fold rapidly without any detectable intermediates.

Here, we have studied a model polymer that folds to a unique native structure through a folding pathway that is characterized by sudden, cooperative transitions between several distinct, partially folded intermediates. These intermediates are obligatory steps in the folding pathway. They also are thermodynamically metastable “phases” of the polymer under native conditions, in the sense that they correspond to local free-energy minima. Thus, these intermediates represent both rare equilibrium fluctuations from the native state as well as transient kinetic species in the folding pathway.

The intermediates we observe are naturally identified with the partially unfolded states found by using native-state hydrogen exchange in cytochrome C (33) and RNase H (34). These partially unfolded states (PUFS) must be thought of as metastable thermodynamic states of the protein, because if there were no free-energy barrier between partially unfolded states and the native state, one would find a continuous distribution of hydrogen exchange protection dependences rather than the discrete groupings that are observed.

The identity of metastable equilibrium states and transient kinetic intermediates that we find for our model polymer parallels the situation in RNase H, in which the kinetic folding intermediate has been shown (35) to resemble both a rare partially unfolded state observed in equilibrium under native conditions and the equilibrium molten globule (36–38) stabilized under acid conditions. The intermediates we find also have the qualities of the molten globule-like state that is stabilized under denaturing conditions in lattice models (39). The connection between kinetic intermediates, partially unfolded metastable states, and equilibrium molten globules that we find in our model supports the hypothesis that molten globules represent stabilized versions of intermediate states along the folding pathway (23, 24, 40).

The intermediates we find are qualitatively different from those observed in other theoretical studies. Previous simulations of other protein-like heteropolymers that use different models and/or polymer lengths found intermediates which are either misfolded (8, 28, 29, 41) or correspond to the folding of domains (42). In their studies of 36-mers with a sequence model, Shaknovich and coworkers (28, 29) find intermediates that are characterized as off-pathway traps that lead to slower folding than in the absence of intermediate. For some longer chains, multidomain behavior was observed (42) in which partially folded intermediates can be observed as the equilibrium state under some conditions. Guo and Thirumalai (41) have found misfolded intermediates in an off-lattice model. Based on their studies of 27-mers, Onuchic et al. (8) have also stressed that intermediates appear as off-pathway traps that slow folding. By contrast, the partially folded, metastable states we find have no non-native structure, and are on-pathway intermediates in the sense that folding can proceed directly to the native state. Our model shows that intermediates are not necessarily a consequence of trapping in a misfolded conformation.

A Classical Folding Pathway.

We have characterized the folding pathway of a protein-like heteropolymer on a three-dimensional lattice by directly simulating a collection of folding events. This polymer is protein-like in the sense that it rapidly folds to a reproducible, native state from any of a vast number of unfolded conformations. By determining the folding mechanism of such a simplified model, we can study in detail the manner in which the Levinthal entropy of the unfolded state is lost as the polymer folds.

The particular polymer we have studied folds via well-defined, partially folded, on-pathway intermediates. This is consistent with a classical pathway (11, 43, 44), which envisions protein folding as an intramolecular chemical reaction that proceeds from the unfolded state to the native state through a sequence of transiently populated intermediates. The species along this pathway are to be viewed as thermodynamically metastable phases of the polymer, separated by cooperative transitions.