Biodiversity and ecosystem productivity in a fluctuating environment: The insurance hypothesis

Abstract

Although the effect of biodiversity on ecosystem functioning has become a major focus in ecology, its significance in a fluctuating environment is still poorly understood. According to the insurance hypothesis, biodiversity insures ecosystems against declines in their functioning because many species provide greater guarantees that some will maintain functioning even if others fail. Here we examine this hypothesis theoretically. We develop a general stochastic dynamic model to assess the effects of species richness on the expected temporal mean and variance of ecosystem processes such as productivity, based on individual species’ productivity responses to environmental fluctuations. Our model shows two major insurance effects of species richness on ecosystem productivity: (i) a buffering effect, i.e., a reduction in the temporal variance of productivity, and (ii) a performance-enhancing effect, i.e., an increase in the temporal mean of productivity. The strength of these insurance effects is determined by three factors: (i) the way ecosystem productivity is determined by individual species responses to environmental fluctuations, (ii) the degree of asynchronicity of these responses, and (iii) the detailed form of these responses. In particular, the greater the variance of the species responses, the lower the species richness at which the temporal mean of the ecosystem process saturates and the ecosystem becomes redundant. These results provide a strong theoretical foundation for the insurance hypothesis, which proves to be a fundamental principle for understanding the long-term effects of biodiversity on ecosystem processes.

Recently the effects of biodiversity on ecosystem processes have received much attention because of the growing concern that loss of biodiversity may impair ecosystem functioning (1–5). A number of experiments have been performed or are in progress (see e.g. ref. 6) and theoretical studies are emerging in this area (7, 8). However, most of these studies are restricted to situations where environmental fluctuation is negligible or excluded (but see refs. 9–12). In the long term, all ecosystems are bound to experience environmental changes (13). Therefore a critical question is: how are ecosystem processes affected by biodiversity or by a loss of biodiversity in a fluctuating environment?

The insurance hypothesis so far has been an intuitive idea that increasing biodiversity insures ecosystems against declines in their functioning caused by environmental fluctuations (12, 14–16). Such an effect is expected because different species respond differently to environmental changes, hence the contribution of some species to ecosystem processes may decrease while that of others may increase when the environment changes. Thus greater species richness should lead to a decreased variability in ecosystem processes because of compensation among species. Here we define insurance effects of biodiversity more generally as any long-term effects of biodiversity that contribute to maintain or enhance ecosystem functioning in the face of environmental fluctuations. These effects may differ depending on the type of fluctuations experienced and the ecosystem properties regarded as desirable, such as long-term average performance, reduced variability, long-term probability of persistence, or resilience to pulse perturbations.

New theoretical studies have started to emerge on these issues (17–20). However, the generality and implications of the insurance hypothesis in real ecosystems are still unclear because of the specific assumptions and analyses made in these studies. Here we present a stochastic dynamic model to show that (i) this hypothesis is expected to be true under very general conditions within a trophic level or functional group; (ii) species richness may not only decrease the temporal variance of ecosystem processes but also increase their temporal mean; and (iii) the species richness beyond which an ecosystem becomes redundant depends on the way the various species respond to environmental fluctuations. We take ecosystem productivity as an example of an important ecosystem process, but our results can be easily generalized to other processes.

THE MODEL

We develop a stochastic dynamic model to assess the effects of species richness within a trophic level or functional group on the expected temporal mean and variance of ecosystem productivity based on individual species’ productivity responses to environmental fluctuations. The model consists of the following three elements.

Replicate Ecosystems.

A set of replicate ecosystems is constructed at each level of species richness by random sampling from a species pool. This procedure corresponds to recent experimental protocols, which is necessary to separate the effects of diversity on ecosystem functioning from combinatorial effects because of species identity (e.g., ref. 21).

Productivity Response of Each Species.

Each species in an ecosystem is characterized by a specific productivity response to environmental fluctuations. We assume that the productivity of species i at time t obeys an unspecified stochastic process and hence is a random variable of time, X_i(t). Discrete time is chosen for mathematical convenience. Each species’ productivity is assumed to take on values between 0 and 1 (0 ≤ X_i(t) ≤ 1) without loss of generality.

Total Ecosystem Productivity.

The total productivity of a replicate ecosystem with species richness n at time t, X(t:n), is a function of the individual species’ productivities at that time and is also a stochastic process:

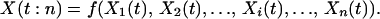1

In this model, we measure the magnitude of an ecosystem process by the temporal mean of that process, X_n = (1/T) Σ_tX(t:n), and the temporal variation of the process by its temporal variance, V_n = (1/T) Σ_t(X(t:n) − X_n)². When an ecosystem is subjected to environmental fluctuations, its processes do not have a stable equilibrium value. Using other measures of temporal variation, such as the coefficient of variation, CV_n = 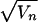/X_n, does not change our results qualitatively. The expected values of the temporal mean and variance of total productivity, E_e[X_n] and E_e[V_n], respectively, are then calculated as functions of species richness by averaging X_n and V_n over all replicates (Appendix):

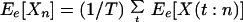2

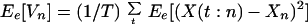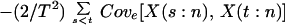3

where Var_e[.] and Cov_e[.] denote expected variance and covariance, respectively, and Var_T[.] denotes temporal variance.

RESULTS

The results depend on the way total ecosystem productivity is determined by the individual species’ productivities. We analyze two limiting cases here: (i) determination by dominance, i.e., total productivity at any time is approximated by the productivity of the most productive species because of interspecific competition:

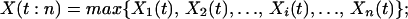4a

(ii) determination by equivalence, i.e., total productivity is simply the average of the individual species’ productivities because interspecific interactions are negligible:

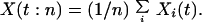4b

Equivalence was implicitly assumed in some previous works (17, 19), but determination by dominance is likely in grassland ecosystems where a single resource limits plant growth (7). Plant competition experiments showed that the yield of two-species mixtures often was close to the yield of the most productive monoculture (e.g., refs. 22–24). Thus, the real determination of total productivity is expected to generally lie between these two limiting cases.

Determination by Dominance.

The effects of species richness on the expected values of the temporal mean, E_e[X_n], and variance, E_e[V_n], of productivity depend on the degree of asynchronicity of the species responses as follows (see proof in the Appendix). (i) If the responses of all species are perfectly positively correlated, i.e., the coefficient of correlation, r_ij, between X_i(t) and X_j(t) is equal to 1 for all pairs of species i and j, then, for any n ≥ 2,

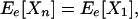5a

6a

(ii) Otherwise,

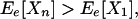5b

and, for sufficiently large n,

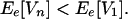6b

Thus, in the highly unlikely case when there is no asynchronicity at all in the species responses, the ecosystem behaves exactly as a single species. In all other cases, E_e[X_n] is greater than E_e[X₁] and E_e[V_n] is smaller than E_e[V₁] for a large enough species richness n. Furthermore, unless all pairs of species responses are perfectly correlated (either positively or negatively, i.e., |r_ij| = 1), E_e[X_n] increases to its maximum value (in this case, 1) and E_e[V_n] decreases to zero as species richness n increases (Figs. 1 and 2A). These effects occur irrespective of any autocorrelation in individual species responses. The autocorrelation of total productivity can be shown to vanish as species richness increases (Appendix); in other words, the total ecosystem response can be regarded as an independent process when species richness is large.

Figure 1.

Determination by dominance: simulations of productivity fluctuations through time in a replicate ecosystem with increasing species richness, n. The horizontal line in each graph shows the temporal mean of ecosystem productivity. Note that the temporal variance decreases while the temporal mean increases as species richness increases. Species responses are independent stochastic processes, and the probability density distribution is a uniform distribution on [0, 1].

Figure 2.

Productivity-diversity relationships in the two cases of determination by dominance (A) and determination by equivalence (B): expected values of the temporal mean of productivity, E_e[X_n] (Eq. 2) and temporal variance of productivity, E_e[V_n] (Eq. 3) as a function of species richness, n. r is the correlation coefficient of species responses; r = 0, 1, and ± 1 correspond to the cases of independent responses, perfect positive correlation, and perfect correlation (including negative correlation), respectively. Note that when r = 1, i.e., when there is no asynchronicity at all, no insurance effects occurs. The probability density distribution is a uniform distribution on [0, 1].

Determination by Equivalence.

In contrast to the previous case, the expected temporal mean of productivity is now constant irrespective of species richness n (Appendix):

7

If the responses of all species are perfectly positively correlated (r_ij = 1 for all pairs of species i and j), then, for any n,

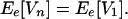8

Otherwise, E_e[V_n] can be either smaller or greater than E_e[V₁], and thus the behavior of E_e[V_n] as a function of species richness n can be complex and idiosyncratic (16) depending on the details of the system because of the correlations between species responses at different times (Appendix). In the special case when these responses are independent, E_e[V_n] becomes smaller than E_e[V₁] for a sufficiently large n and converges to the minimum value Var_T[E_e[X(t:1)]] (Fig. 2B). Note that Var_T[E_e[X(t:1)]] is the temporal variance of the expected productivity at each time, and thus vanishes if the species responses have no directional trend in time (i.e., E_e[X(s:1)] = E_e[X(t:1)] for any s, t).

Productivity-Diversity Pattern.

The pattern of average ecosystem productivity as a function of species richness and the degree of ecosystem redundancy can be greatly affected by both the species responses and the degree of asynchronicity of these responses in the ecosystem. Here, we call an ecosystem redundant (16, 19, 25) for some functional process if this process has attained a plateau for a lower value of species richness and is not enhanced by the addition of further species in the system. We examine in particular the effect of the variance of each species response, Var[X_i(t)], on the species richness required for an ecosystem to become redundant.

Assume that total ecosystem productivity is determined by dominance of the most productive species, and all species responses are independent of each other and obey the same stochastic process. Further assume that the mean of the response is 1/2, as in the β-distribution (Fig. 3A), in which case the variance of the species response may be viewed as a measure of a species’ contribution to maximum ecosystem productivity (in this case, 1). This is because a greater variance means a greater probability of a species taking on the maximum productivity at each time. The results are summarized in Fig. 3B. For a given species richness, as the variance of the species response increases, the temporal mean of ecosystem productivity is elevated, that is, the effect of species richness is enhanced. But as a result, the species richness beyond which the ecosystem is redundant also decreases.

Figure 3.

(A) Representative shapes of the β-distribution (27) used to describe the species responses in B:

For our purpose, we put β = α. Each distribution has the same mean 1/2 and is symmetrical in relation to x = 1/2. Note that as α decreases, the variance of the distribution increases; as a result, the probability that each species takes on maximum productivity (in this case, 1) increases. Thus changing α amounts to changing the variance. (B) Productivity-diversity relationships generated by changing the variance of species responses: expected value of the temporal mean of ecosystem productivity as a function of species richness, in the case where ecosystem productivity is determined by dominance and species responses are independent and follow a β-distribution as in A. Note that, as the variance of species responses increases (i.e., α decreases), the expected value of the temporal mean of ecosystem productivity increases monotonically for a given species richness, and thus attains its maximum value of 1 at a smaller species richness.

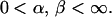DISCUSSION

This work shows two major effects of species richness on ecosystem productivity in a fluctuating environment: (i) a reduction in the temporal variance of productivity, in short a buffering effect, and (ii) an increase in the temporal mean of productivity, in short a performance-enhancing effect. We call both these effects insurance effects in agreement with our definition (see Introduction) because they both contribute to maintain or enhance ecosystem functioning in the face of environmental fluctuations.

Under what conditions can we expect such insurance effects to occur in an ecosystem? Our results show that asynchronicity of the species responses to environmental fluctuations is the basis for the buffering effect. In the extreme case of an ecosystem with only one species in a functional group, a low productivity of this species at a time results directly in a low ecosystem productivity at that time. On the other hand, in an ecosystem with a high species richness, species with high as well as low productivities can be expected to occur because of asynchronicity of their responses, so that a low productivity in some species does not necessarily affect ecosystem productivity. The origin of asynchronicity of species responses does not matter; it can be generated in many ways, whether by competitive release, physiologically determined differences in the response to environmental fluctuations or purely stochastic effects. On the other hand, the performance-enhancing effect needs, in addition to asynchronicity, some adaptive mechanism that gives greater weight to those species that perform better in each environmental condition, for example, selection by interspecific competition in the case of determination by dominance. In this case, the variation in productivity increases with species richness at any time and the selection process through dominance picks up the most productive species within this variation; as a result, productivity increases with species richness. In contrast, in the case of determination by equivalence, the mean ecosystem productivity remains constant irrespective of species richness because high and low productivities cancel each other out around the mean.

Regarding the buffering effect in the case of determination by equivalence, we obtain qualitatively similar results as those obtained by previous authors who used a different approach and more restrictive assumptions (17, 18). In these studies, total community productivity (biomass) was kept constant, and the variance of individual species’ productivity responses were assumed to be related to the mean by a power-law relation. Our results show that the buffering effect does not depend on these particular assumptions. In our modeling framework, these assumptions are not necessary but can be derived as consequences for a special case. Further, our model shows that correlations between species responses can cause more complicated behaviors.

For the present analysis, we assumed that all species have the same response range, 0 ≤ X_i(t) ≤ 1 (Appendix). This assumption, however, can be easily relaxed, which leads to slightly different predictions (unpublished results). For instance, in the case of determination by dominance, if there are two types of species A and B, such that species A always have a productivity that is higher than that of species B, there is no difference as regards ecosystem productivity between a monoculture of one species A and a mixture of one A plus any number of B. That is, species with a consistently low productivity have no contribution to insurance effects, whatever their species richness. If species response ranges overlap each other, however, all contribute to insurance effects.

The importance of insurance effects is thus determined by three factors: (i) the way ecosystem productivity is determined by individual species responses to environmental fluctuations, (ii) the degree of asynchronicity of these responses, and (iii) their detailed characteristics including their range of variation. To what extent are insurance effects expected to be present in real ecosystems? On a long enough time scale for significant environmental fluctuations to take place, species response ranges are likely to usually overlap, and some degree of asynchronicity of responses seems inevitable if we remember the high dimensionality of the physiological niche space to which each species responds. As already mentioned earlier, the real determination of total productivity also should lie between the two extremes considered here, i.e., determination by dominance and determination by equivalence. Only a slight selection mechanism favoring species that are better adapted to current environmental conditions and have a higher than average productivity under these conditions would suffice to deviate from the perfect determination by equivalence and lead to a performance-enhancing effect. Thus, it seems highly probable that species richness has both a buffering and a performance-enhancing effect in real ecosystems in the long term. Recent experimental evidence on ecosystem predictability in aquatic microcosms (11, 12) does support the buffering effect. The performance-enhancing effect awaits experimental tests; it is likely to be more commonly found in communities governed by strong competition for a limiting factor, such as terrestrial plant communities. Food-web configuration may play a critical role in more complex ecosystems, which we have ignored deliberately here, the productivity of each trophic level being likely to depend on features such as the number of trophic levels (26), etc.

Our model also shows that the variance of the species responses has a significant effect on the productivity-diversity pattern and on the species richness required to reach ecosystem redundancy. Consider the two limiting cases when the variance of the species responses is maximum (α = 0) and zero (α = ∞) in Fig. 3B. When variance is maximum, because each species has a high probability of achieving the maximum productivity at any time, the ecosystem becomes redundant at a relatively small number of species (typically, of the order of 10). All the additional species above the first 10 species have little effect on total ecosystem productivity. On the contrary, when variance is minimum, each species has a very small probability of achieving the maximum productivity, and thus the species richness at which the ecosystem becomes redundant is infinite. Thus, the higher the probability each component species has to contribute to an ecosystem process, the lower the species richness at which this process saturates and the ecosystem becomes redundant.

This result can have profound consequences from a conservation point of view (2). Suppose that the species richness of an ecosystem is being reduced from, say, 100 species. If the ecosystem can be regarded as randomly constructed from a pool of species with little temporal variability, as might be the case for some tropical ecosystems, ecosystem productivity is expected to decrease gradually and roughly linearly. On the other hand, if it is composed of species with highly variable responses, as might be the case in temperate ecosystems, the change in ecosystem productivity is expected to be nonlinear and sudden. Ecosystem productivity would be maintained close to its maximum value as long as species richness is high enough for the ecosystem to be redundant, but would decline abruptly when species richness is further reduced beyond this point. Thus the characteristic responses of component species may greatly affect the response of ecosystem performance to changes in biodiversity.

Appendix

We define the response range of species i, [a_i, b_i], as the range of productivity values that species i can take on with a positive probability, where the inequality 0 ≤ a_i ≤ b_i ≤ 1 holds. For simplicity, we assume in the following that the response range of any species at any time is [0, 1], but this restriction can be easily relaxed.

Determination by Dominance.

Let q(x₁, x₂, … , x_n, t) be the joint probability density distribution of X_i(t) (i = 1, 2, … , n), i.e., the joint probability density with which each species i has productivity x_i at time t, and q(x₁, x₂, … , x_n, t|y₁, y₂, … , y_n, s) the joint conditional probability density with which each species i has productivity x_i at time t under the condition that it had productivity y_i at time s (s < t). Similarly, let p_n(x, t) and p_n(x, t|y, s) be the probability density distribution and conditional probability density distribution of X(t:n), respectively.

E_e[X_n] and E_e[V_n] are expressed in terms of E_e[X(t:n)], Var_e[X(t:n)] and Cov[X(s:n), X(t:n)] as in Eqs. 2 and 3, and thus rewritten in terms of E_e[X^k(t:n)] (k is a positive integer) and E_e[X(s:n)X(t:n)]. These in turn can be expressed in terms of the probability density distributions as follows:

A1

A2

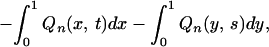where

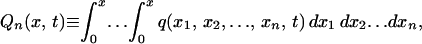A3

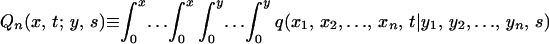A4

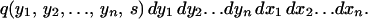Eqs. A1 and A2 are obtained by partial integration after substituting the following two equations (which are derived on the basis of elementary probability calculus) into them:

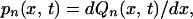A5

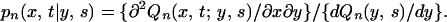A6

The following propositions are obtained from Eqs. A1–A6 except in the special case where all pairs of species responses are perfectly correlated.

Proposition 1.

p_n(x, t) converges to the delta function δ(x − 1) as species richness n increases.

Proposition 2.

E_e[X(t:n)] increases monotonically with species richness n toward the maximum possible productivity in the species pool (in this case, 1). As a result, the expected value of the temporal mean of productivity, E_e[X_n], follows the same behavior.

Proposition 3.

Var_e[X(t:n)] decreases toward zero for a sufficiently large species richness.

Proposition 4.

Cov_e[X(s, n), X(t, n)] converges to zero as species richness n increases. This means that the autocorrelation of the stochastic process X(t:n) vanishes for a sufficiently large species richness.

Proposition 5.

E_e[V_n] vanishes for a sufficiently large species richness.

The proofs of Propositions 2–5 follow directly from proposition 1 and can be obtained on request.

Proof of Proposition 1.

Because Q_n(x, t) in Eq. A1 is a cumulative probability distribution of X(t:n), 0 ≤ Q_n(x, t) ≤ 1 holds, and Q_n(x, t) is a nonincreasing function of species richness n:

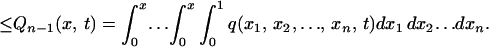A7

When the inequality holds in Eq. A7, Q_n(x, t) converges monotonically to zero because the hypervolume xⁿ of the integration range of variables x₁, x₂, … , x_n is embedded in the n-dimensional hypercube [0, 1]ⁿ and converges monotonically to zero as n increases as long as x < 1. It follows that the last term in the right-hand side of Eq. A1 decreases monotonically to 0. Thus, E_e[X^k(t:n)] increases monotonically to 1, which means that p_n(x, t) converges to δ(x − 1) because the characteristic functions of these two functions coincide at the limit n → ∞.

When all pairs of species responses are perfectly correlated, i.e., |r_ij| = 1 for all i and j, either X(t:n) = X₁(t) for any n ≥ 1 (r_ij = 1) or X(t:n) = X₁(t) for n < k and X(t:n) = max {X₁(t), X_k(t)} for n ≥ k (r_ij = −1 for at least one pair) holds, where k is the smallest integer such that X₁(t) ≠ X_k(t). This means that either Q_n(x, t) = Q₁(x, t) for any n ≥ 1 or Q_n(x, t) = Q₁(x, t) for n < k and Q_n(x, t) = Q_k(x, t) for n ≥ k.

Determination by Equivalence.

It follows directly from Eq. 4b that:

A8

The right-hand side of Eq. A8 is the expected productivity of a monoculture, E_e[X(t:1)]. Therefore, using Eqs. 2, Eqs. 7 and A9 follow.

A9

The variance and covariance terms in Eq. 3 then can be further expressed as follows:

A10

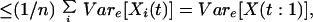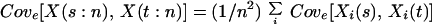A11

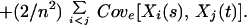Because Σ_i<jCov_e[X_i(s), X_j(t)] can take on both positive and negative values depending on the combination of species responses in the ecosystem, from Eq. 3, E_e[V_n] can be greater than E_e[V₁] and behave idiosyncratically as a function of species richness. Here, for further analysis, we focus on three limiting cases, where Var_e[X_i(t)] ≡ Var(t) for all i is assumed for simplicity.

Independent responses:

r_ij = 0 for all i, j.

A12

A13

Thus, E_e[V_n] converges to Var_T[E_e[X(t:1)]] at a speed of O(n).

Perfect positive correlation in responses:

r_ij = 1 for all i, j.

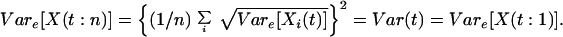A14

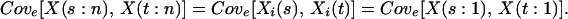A15

Thus, from Eqs. 3 and A9, E_e[V_n] = E_e[V₁] holds.

Perfect correlation in responses:

|r_ij| = 1 for all i, j.

Species can be classified into two groups, say A and B, such that any two species in the same group have a perfect positive correlation in their responses (r_ij = 1), while any two species in different groups have a perfect negative correlation in their responses (r_ij = −1). Assume that the two groups have the same number of species, m (hence, n = 2m). In this case,

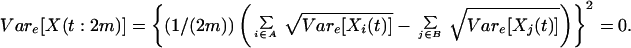A16

If i and j belong to the same group, Cov_e[X_i(s), X_j(t)] = Cov_e[X_i(s), X_i(t)]. Otherwise, Cov_e[X_i(s), X_j(t)] = −Cov_e[X_i(s), X_i(t)]. It follows that:

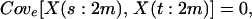A17

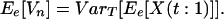A18

If the two groups have unequal numbers of species, e.g. m and m + 1, it can be shown similarly that E_e[V_n] converges to Var_T[E_e[X(t:1)]] but with oscillations.