A relation between the principal axes of inertia and ligand binding

Abstract

The principal axes of inertia are eigenvectors that can be calculated for any rigid body. We report studies of the position of the principal axes in crystallographically solved protein molecules. We find with high frequency that at least one principal axis penetrates the surface of the respective protein in a region used for ligand binding. In antibody variable regions, an axis goes through the third hypervariable loop of the heavy chain. In major histocompatibility complex proteins, an axis goes through the peptide-binding groove. In protein–protein heterodimers, a principal axis of one subunit will often penetrate the interface formed with the other subunit. In many of these protein–protein complexes, the axis specifically intersects residues known to be critical for molecular recognition.

The stability of protein–protein complexes depends on chemical complementarity at the contact surfaces of interacting proteins, primarily in the form of short-range interactions such as hydrogen bonds. Could an interaction surface be located anywhere on a molecule? Protein-sized molecules are thought to react with each other first by forming an encounter complex, in which the reactants collide repeatedly as they rotate and translate across each other's surfaces (1–3). The spatial distribution of collisions might not be isotropic but may occur preferentially in regions determined by the gross geometry of the reactants (4). If so, such regions might be advantageous locations for ligand-binding sites. Here we report a frequent association of ligand-binding sites with the principal axes of inertia, a structural feature determined by gross molecular geometry.

The principal axes of inertia of a rigid body are a set of axes passing through the object's center of mass and relate to the object's mass distribution such that angular momentum imparted about a principal axis is not transferred to any other axis. The symmetry axis of a child's top is one example of a principal axis. A top spun about this axis will continue spinning until friction has nearly depleted its angular momentum. In contrast, spinning the top about an arbitrary axis produces motion that rapidly becomes disorderly. An asymmetric rigid body has three mutually perpendicular principal axes, which can always be calculated unambiguously.

In this paper, we examine the principal axes of crystallographically solved molecules whose biological function entails ligand recognition. We looked first at polymorphic molecules of the immune system, which recognize ligands of diverse chemical nature. In the antigen-binding region of antibodies (Fv fragment), one principal axis almost invariably goes through the area of the highest sequence diversity. A similar observation holds for the T cell antigen receptor (TCR). In major histocompatibility complex (MHC) molecules, whose function is to bind antigenic peptides, a principal axis intersects the peptide-binding groove. We also examined monomorphic proteins that have evolved to recognize specific protein ligands and found that in most cases a principal axis intersects the interface of protein–protein complexes. Here we document that the ligand interaction surfaces of proteins frequently lie on a principal axis and suggest that this observation reflects a fundamental aspect of ligand binding.

Methods

Atomic coordinate sets were obtained from the Protein Data Bank (PDB). The moment of inertia matrix for each molecule or portion of a molecule was calculated from the coordinates x, y, z, and mass m of each atom k by using the expression (5):

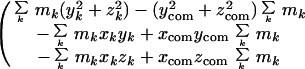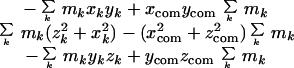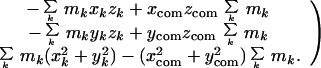Here, the center-of-mass coordinates x_com, y_com, z_com, are given by

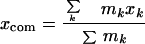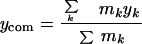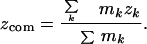A matrix of eigenvectors was in turn generated from the moment of inertia matrix by using mathematica (Wolfram Research, Champaign, IL). The eigenvectors (the principal axes) were either displayed directly, or the transpose of the eigenvector matrix was used as a transformation matrix to align inertial axes along the Cartesian axes, with the center of mass at the origin.

The pseudodyad of antibody Fv fragments was calculated by using the program align (6), as modified by Steven Sheriff (Bristol–Myers Squibb). Homologous pairs of V_H and V_L residues used in the calculation were those assigned by Padlan (7). The program pairs was used to identify intermolecular contact residues. Molecular illustrations were drawn by using molscript (8).

Results

Ig Fvs.

Immunoglobulins are modular proteins composed of ≈110-residue protein domains connected by disulfides or flexible linkers (9). Each domain is usually paired with an identical or heterologous domain through a noncovalent interface. One pair of domains, the Fv, is composed of one domain from the κ or λ light chain (V_L) and a slightly larger domain from the Ig heavy chain (V_H) and represents the functional unit of antigen binding. Somatic diversity-generating mechanisms responsible for antigen recognition operate exclusively on the Fv (10, 11). Three peptide segments in each domain, the complementarity-determining regions (CDRs), are sites of high sequence variability and form nearly all the direct chemical contacts with antigen. Of the six CDRs, CDR-H3 is by far the most variable because of the D gene segments unique to the heavy-chain locus. Incorporation of D segments in CDR-H3 adds a level of combinatorial diversity not available to the other CDRs, and the process of D rearrangement further enhances junctional, N-region, and palindromic nucleotide diversity. Several intact IgG structures have been crystallographically solved, but these are too flexible to be treated as rigid bodies. By contrast, Fv fragments have a stable structure in solution, and their motion within an IgG molecule is minimally constrained by contacts with other domains (12). We therefore focused on the principal axes of Fvs as the most relevant to ligand recognition.

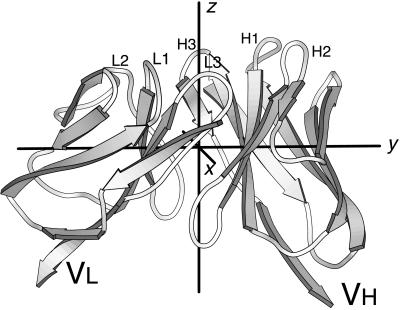
The principal axes lie in distinctive places in an Fv, shown in Fig. 1. The axis designated z lies between subunits and extends from the center of mass of the Fv through the antigen-combining site. The pseudodyad relating V_H to V_L is in the vicinity of z. The y axis passes through the heart of V_H and V_L, intersecting the conserved Trp residue in the “pin” of each Ig domain (13). A second pseudodyad that relates the CDR and antigen-distal ends of each subunit (14) lies in the vicinity of y. The x axis passes between the two subunits, roughly within the plane of the V_H–V_L interface.

Figure 1.

Ig Fv domain with three principal axes. The molecule shown is the antilysozyme antibody D1.3 (PDB 1vfa). Loops from the CDRs are at the top and are labeled H1, H2, etc. The three principal axes of the Fv are labeled x, y, and z.

The principal axes of antibody variable regions are not sensitive to sequence variation. Roughly one-fourth of residue positions in an Ig variable domain are hypervariable, in that many different residue types are found in these positions (15, 16). To determine the extent to which sequence variability influences the position of the principal axes, we examined the Fv portion of crystallographically solved Ig structures (Table 1) and found that the axes were in nearly identical locations regardless of V gene family, whether the molecule was murine or human, κ type or λ type (data not shown). We conclude that the location of the principal axes is unchanged by somatic diversity-generating mechanisms or the evolutionary divergence of mice and humans, therefore it is general for antibody Fv domains.

Table 1.

PDB files used for analysis of immunoglobulin Fv regions

1acy	1baf	1bbd	1bbj	1cbv	1cgs	1clo	1clz	1dba	1dfb
1dvf	1fai	1fbi	1fgv	1fig	1flr	1for	1fpt	1frg	1fvc
1gaf	1ggi	1ghf	1gig	1iai	1ibg	1igc	1igi	1igm	1igt
1ikf	1ind	1jel	1jhl	1kel	1kno	1mam	1mco	1mfe	1mlb
1mrc	1ncd	1ngp	1nld	1nma	1nsn	1opg	1plg	1rmf	1tet
1vfb	1vge	1vir	1yuh	2cgr	2fb4	2fbj	2fgw	2igf	2mcp
3hfl	3hfm	6fab	7fab	8fab

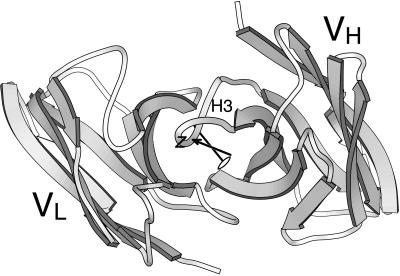
Although Fv molecules are heterodimers, a pseudodyad relates positions in the V_H domain to homologous positions in the V_L domain (17). This axis is used to calculate elbow angles in Fab structures. Principal axes of rigid bodies frequently coincide with symmetry axes, hence we asked whether z and the pseudodyad were coincident. The illustration in Fig. 2 showing an Fv fragment with both z and the pseudodyad drawn typifies the relation we observed. No point-to-point homology exists between the heavy-chain and light-chain CDRs, hence conserved residues in the β-sheet framework are used to define the pseudodyad. The pseudodyad therefore does not run midway between H3 and L3 but is slightly closer to H3. The z axis is determined by mass distribution of the entire Fv rather than symmetry of a subset of residues and is even further from the H3–L3 midpoint than is the pseudodyad. The displacement seen in Fig. 2 is caused only partly by the V_H domain having about 5% greater mass than V_L. This mass disparity accounts for a translation of ≤1 Å of the principal axes' origin toward V_H. More significant is a subtle mass distribution that yields an angular deflection of z through CDR-H3.

Figure 2.

Ig V_H and V_L domains, seen from an “antigen-eye view.” The molecule used is MOPC 603 (PDB 2 mcp). The principal axis, z, which extends through CDR-H3, is drawn with an arrowhead, and the pseudodyad axis is drawn with a dyad symbol.

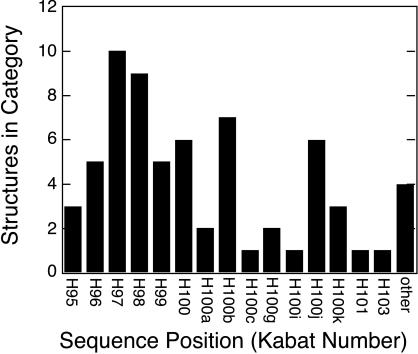
We mapped surface residues of Fv and Fab structures that are nearest the z axis (calculated for Fv regions in the case of Fabs) and found the same residue positions repeatedly intersected, as shown in Fig. 3. The axis, with 5 exceptions of 66 structures, passes through Kabat residues H95 to H101, all of which are part of CDR-H3 (18). Most of these residues are encoded by the D gene segment and N-region nucleotides. In summary, the antibody region most critical for antigen recognition lies precisely on a principal axis.

Figure 3.

Intersection of z principal axis with CDR-H3 in antibody structures. Principal axes for 66 Ig Fv domains (Table 1) were calculated, and in each case the surface residue nearest to z was identified by inspection. The Kabat sequence number of each intersecting residue was determined, and the number of instances for each Kabat position is shown (18). Residues H95 through H102 form CDR-H3. The adjacent residue H103 is a framework residue; all other exceptions are grouped in the category “other.”

Axis Shift in TCR.

TCRs of the αβ type are surface molecules that recognize short peptide antigens embedded in the binding groove of MHC molecules on antigen-presenting cells. The extracellular portions of TCRs resemble antibody Fab fragments in having two chains with N-terminal variable domains (Vα and Vβ). All domains follow an Ig fold, and each variable domain has three CDRs, analogous to those in antibodies. Analysis of TCR crystal structures suggests the z principal axis is associated with a region of critical sequence diversity.

We calculated the position of principal axes in four TCR Fvs and found the axes similar to those in antibody Fvs. In the murine 2C Vα–Vβ dimer (19) and the human A6 TCR (20), the z axis passes through residue 100 in CDR3 of the Vα chain. In the scFv version of murine TCR KB5-C20 (21), z intersects residue 97 of Vα, which is also in CDR3. In the murine TCR N15 (22), z passes between domains but is closest to residue 104, in CDR3 of Vα. Contacts between the Vβ and Cβ domains are more extensive than in antibodies (23), hence the TCR extracellular domains may lack the flexibility of an antibody Fab. Consequently, we also calculated the principal axes of the entire extracellular region of TCR N15. Inclusion of the two constant domains left the position of z almost unchanged; again z passed midway between domains, closest to residue 102 in Vα, in CDR3.

The association of z with Vα CDR3 cannot be merely a reflection of homology with antibodies, because the TCR Vα domain is closer in three-dimensional structure to Ig V_L domains (24), whereas in antibodies the z axis goes through V_H domains. TCR V_β domains also superpose more closely on V_L than V_H, but the deviations in atomic position are larger than for the V_α–V_L superposition (23). At the genetic level, the TCR β locus is similar to the Ig heavy-chain locus in utilizing D segments, which are not used in forming TCR α or Ig κ or λ chains. Although the TCR α locus does not have D segments, the potential combinatorial diversity of Vα appears to be much greater than Vβ. The TCR α locus has 42 or more V gene segments to combine with 61 J segments (25–27), whereas the TCR β locus has 46 functional V gene segments, 13 J segments, and two D segments, only one of which can join with all of the Js (28). Furthermore, the TCR α locus can rearrange continuously in unselected cells, on both chromosomes, until a receptor structure is generated that allows positive selection (29). No secondary rearrangement process has been reported for the TCR β locus. To summarize, the limited crystallographic data on TCRs point to a principal axis coinciding with a key ligand recognition element.

MHC–Peptide Interactions.

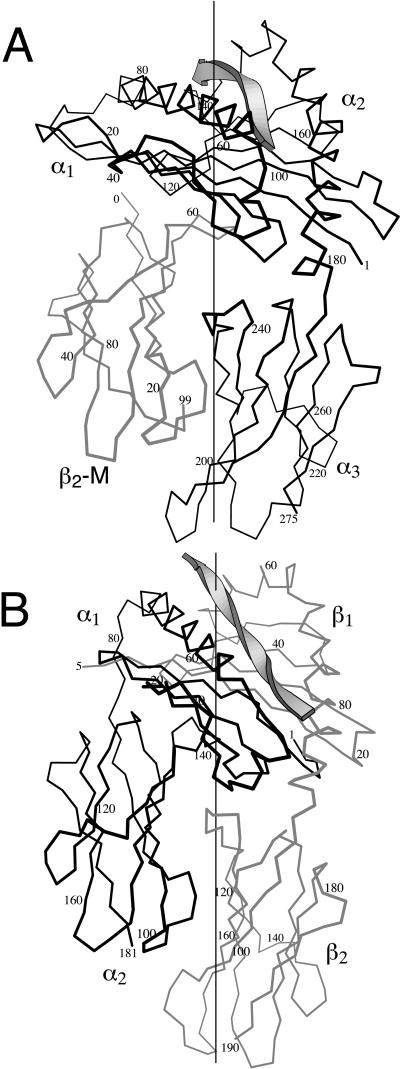
If the evolution of ligand-binding sites on principal axes reflects a fundamental aspect of molecular recognition, the same correlation should be evident in other types of macromolecular interactions besides antibody–antigen. We therefore examined the position of principal axes in peptide complexes with MHC extracellular domains. MHC molecules are heterodimeric proteins that bind antigenic peptides during assembly in the endoplasmic reticulum, and subsequently maintain these peptides in an exposed position on the cell surface. Class I MHC molecules have a polymorphic chain with three domains. Peptides bind in a groove between domains α₁ and α₂. These two domains have a unique fold, whereas the α₃ domain and the second chain, β₂-microglobulin, each have an Ig fold and do not contribute to specificity. The extracellular region of class II molecules consists of two polymorphic 2-domain chains, α and β. The α₁ and β₁ domains are structurally similar to the α₁ and α₂ domains of class I and also form a peptide-binding groove between them. The α₂ and β₂ domains form Ig folds.

We calculated the principal axes of the MHC structures in Table 2. In every case, one axis intersected the peptide within a tightly bounded portion of the peptide–MHC interface, shown in Fig. 4. In class II molecules, the axis intersected position P8 within the specificity-determining portion of the bound peptide, the single exception in Table 2 being an intersection with the adjacent position P7. Class I molecules are less regular than class II in correspondence between peptide position and binding pocket for peptide side chain; nevertheless, six conserved pockets in the peptide-binding groove of class I have been defined (30). One principal axis always passed near the nexus of pockets B, C, and D. Residues forming pocket C invariably intersected this axis. The TCR region interacting with this site is known in one case. In the complex of human TCR A6 with human HLA 0201 (20), the axis of the class I molecule passes through the edge of the TCR footprint and extends into residues L98, A99, and G100 in CDR3 of the TCR Vβ chain. To summarize, the region of MHC molecules most critical for ligand recognition is built around a principal axis.

Table 2.

Principal axes in MHC–peptide complexes

PDB no.	Molecule	Class	Species	Peptide residue nearest axis	Pocket(s) intersected
1a1n	HLA-B3501	I	Human	M6	C
1agd	HLA-B0801	I	Human	K5	C, D
1bii	H-2Dd	I	Mouse	R405, A406, F407	B, C
1hhi	HLA-A0201	I	Human	F7	B, C, D
1hoc	H-2Db	I	Mouse	N5	B, C
1ld9	H-2Ld	I	Mouse	N5, I6	B, C
1mhc	H-2M3	I	Mouse	F3	B, C
1osz	H-2Kb	I	Mouse	Y5	B, C
3hla	HLA-A2.1	I	Human	—	B, C
1a6a	HLA-DR3	II	Human	L98	P8
1aqd	HLA-DR1	II	Human	H12	P8
1iak	I-Ak	II	Mouse	N59	P8
1iea	I-Ek	II	Mouse	L8	P8
2iad	I-Ad	II	Mouse	S135	P8
2seb	HLA-DR4	II	Human	G1178	P7

Figure 4.

Principal axis in MHC molecules. (A) Human class I MHC molecule HLA-A0201 (PDB 1hhi). The backbone of the bound antigenic peptide is represented by a ribbon. The black line traces the α carbons of the α chain. The gray line traces the chain of β2 microglobulin. The vertical line represents a principal axis that passes through the peptide-binding groove. (B) Mouse class II MHC molecule I-A^k (PDB 1iak). The peptide and principal axis are as in A. Heavy lines trace the α chain and gray lines, the β chain.

Protein–Protein Interactions.

Complexes of proteins are another class of crystallographically solved structures that we examined for a correlation between principal axes and ligand-binding sites. Although this class is immense, two criteria we applied excluded many protein complexes. First, structures representing a fragment of a larger protein were excluded, because we cannot calculate from such structures the true position of the principal axes in the complete molecule. As was done for antibodies, an exception was made for fragments that represent an independent domain with considerable motional freedom, such as the IL-1 receptor extracellular domain. Criteria for independence were resistance to proteolysis and retention of function. Second, we excluded protein complexes with internal symmetry. Principal axes necessarily coincide with molecular symmetry axes, and arguments could be made in these cases that protein symmetry is a necessary structural feature, not principal axis proximity per se. For example, the regulatory subunit dimers of aspartate transcarbamylase have 2-fold axes, which coincide with the molecular 2-fold axes of the holoenzyme (31). Although interfaces along principal axes fit the pattern we describe, the point symmetry of aspartate transcarbamylase is likely to be more functionally significant for the concerted allosteric transition this enzyme is known to undergo (32). To avoid sample bias arising from symmetry, we confined our analysis to monomeric proteins that form heterodimers.

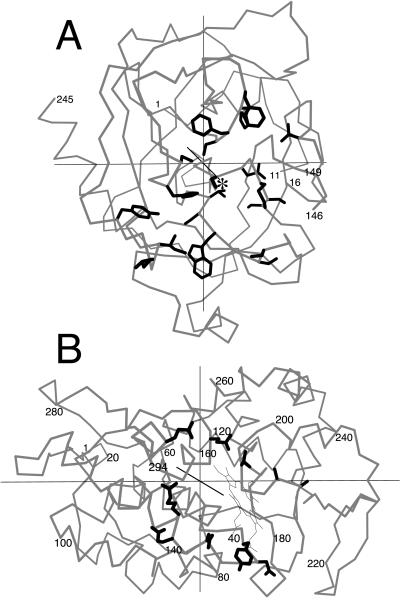
Protein pairs meeting the strictures of completeness and asymmetry are listed in (Table 3). For each protein–protein complex, we determined the residues forming the interface, calculated the principal axes of each subunit of the complex, and asked whether in either subunit an axis passed through the interface contact residues. If no axes hit the interface, that subunit was scored “–,” signifying no apparent association with ligand binding. If an axis did pass through the interface, the example was still not necessarily scored “+” because of an ambiguity arising from the fact that six half-axes penetrate the surface of a globular protein. Because interface regions cover 5–20% of a protein's surface area (33), even an uncorrelated relation between principal axes and ligand binding would result in an axis intersecting some portion of an interface in half of all cases. We therefore scored as positive only the instances in which the axis either passed through the geometric center of the interface or intersected “landmark” residues known from biochemical studies to be functionally important in ligand binding. For example, one principal axis of chymotrypsin (Fig. 5a) intersects residue 195, the essential serine of the catalytic triad. This axis, therefore, is not merely associated with the general vicinity of ligand interaction but intersects the exact point of covalent contact with the protein substrate. Cytochrome c peroxidase is an example of a molecule we score as positive because the interface contact residues form a horseshoe shape with a principal axis running through the center (Fig. 5b).

Table 3.

Principal axes in interface surfaces of protein–protein complexes

PDB no.	Molecule 1	Axis intersects interface	Functional residues or motif intersecting axis	Molecule 2	Axis intersects interface	Functional residues or motif intersecting axis
1bnd	Brain-derived neurotrophic factor	+	Center of contact region	Neurotrophin 3	+	Center of contact region
1cbw	Bovine chymotrypsin	+	S195 (catalytic serine)	Bovine pancreatic trypsin inhibitor	+	K15 (residue in P1 position)
1hia	Kallikrein	+	H57, S195 (catalytic triad)	Hirustasin	+	R32
1ira	IL-1 receptor	+	“A site,” Y124	IL-1 receptor antagonist	+	Q20, Y34
1itb	IL-1 receptor	+	K114, Y127, I240	IL-1β	+	H30, K93, E105
1jsu	Cyclin A/CDK2 heterodimer	+	Center of contact region	p27Kip-1	+	LFG motif
2pcc	Cytochrome c	+	Heme	Cytochrome c peroxidase	+	Center of contact region
1brs	Barnase	+	R87, H102	Barstar	−
1efn	HIV nef C-terminal domain	+	PxxP motif	Fyn tyrosine kinase SH3 domain	−
1fin	Cdk2	+	T160, T-loop	Cyclin A	−
1fss	Fasciculin II	+	R11	Acetyl cholinesterase	−
1lpa	Procolipase	+	E15, L16, R38	Lipase	−
1ycs	p53 core domain	+	R248 (most frequently mutated in tumors)	p53-binding protein 2 SH3/ankyrin domains	−
4cpa	Potato CPA inhibitor	+	Y37, V38 (P2 and P1 positions)	Carboxypeptidase A	−
1agr	Giα1	+	Center of contact region	RGS4	a
1glc	Glucose-specific factor III	+	H90	Glycerol kinase	b
1gua	Rap1a	+	I36	Raf (Ras-binding domain)	c	R59
1ak4	Cyclophilin A	−		HIV capsid N-terminal domain	c
1a2k	RAN	−		Nuclear transport factor 2	b
1dkg	DnaK ATPase domain	−		GrpE	b

a, disqualified; significant fraction of molecule missing in crystal structure; b, disqualified; molecule is symmetric oligomer; c, axis intersects interface but not the central region or a known functional residue. 

Figure 5.

Principal axes in protein–protein complexes. A. Bovine chymotrypsin from the complex with bovine pancreatic trypsin inhibitor (PDB 1cbw). An α-carbon trace is shown in gray. Side chains of residues that contact the ligand are drawn with heavy lines. Ser-195 is marked with an asterisk. (B) Yeast cytochrome c peroxidase from the complex with yeast iso-1 cytochrome c (PDB 2pcc), drawn as in A.

In seven cases in Table 3, one principal axis of each partner in a heterodimer passes through the center or key element of the interface. In seven other cases, an axis passes through the center or key interface element of one subunit but not the other. Of six additional examples where one subunit, but not the other subunit, has been excluded for reasons of symmetry or completeness, three score “+” and three score “–.” Of the 10 negative examples in Table 3, four proteins have clearly not evolved to bind the ligand in the respective crystal structure (1ak4, 1efn, 1fss, and 4cpa). Acetyl choline esterase, for example, has not been under selective pressure to improve binding to fasciclin II, a toxin from green mamba venom. We did not identify any examples of heterodimers in which principal axes of both subunits miss the interface (“−/−”). If principal axis position and ligand binding were uncorrelated, −/− examples should be as numerous as +/+. We interpret this discrepancy, the overall preponderance of positive examples, and the striking intersection of principal axes with landmark residues, as supporting the hypothesis that the coincidence of principal axes and ligand-binding sites reflects function.

Discussion

In the previous section, we have shown that a principal axis of inertia is often associated with the ligand-binding site in major protein classes. In antibody variable regions, one axis almost invariably goes through CDR3 of the heavy chain, the region of the molecule most responsible for antigenic specificity. In TCRs, a similar axis intersects CDR3 of the α chain. In peptide–MHC complexes, a principal axis passes through the peptide and peptide-binding groove, the site of interaction with TCR. Lastly, in binary complexes between structurally dissimilar proteins, a principal axis often intersects key interface residues.

The location of ligand-binding sites along principal axes suggests the action of a subtle but pervasive selective factor acting over evolutionary time. In this hypothesis, the propensity of protein-sized macromolecules to react with each other is not isotropic, but is favored to occur at surfaces near principal axes. Because protein modifications that affect gross geometry, such as covalent labeling with phycoerythrin or creation of gene fusions, necessarily reposition principal axes but generally do not abolish ligand binding, the magnitude of this effect must be small. Therefore, a ligand-binding function that arises de novo might be sited arbitrarily, away from any of the principal axes. The principal axes of antigens, for example, do not generally intersect the epitope region in crystal structures of antibody–antigen complexes. However, receptor mutants that reposition the ligand-binding site closer to an axis would derive a slight energetic advantage and slightly improved fitness that would be selected over many generations.

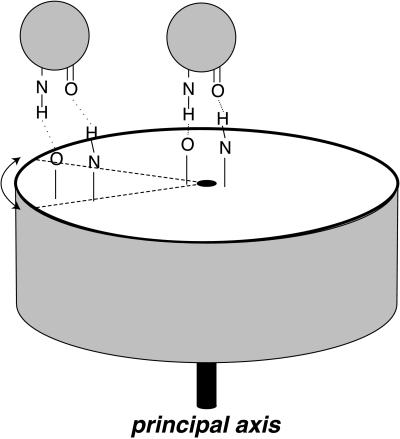
What physicochemical principle underlies the superior genetic fitness of an axial position for a ligand-binding site? Because a principal axis is an eigenvector about which angular momentum is conserved, the selective advantage is most likely related to rotational motions of macromolecules free in solution or in receptor–ligand complexes. If Brownian motion of a domain or complete macromolecule includes a strong rocking component about a principal axis, two advantages are immediately apparent (Fig. 6). First, greater structural stability of a complex arises because the bonds holding a ligand to an interface at the center of this rotational motion would be subject to smaller shear forces than they would at a chemically identical interface remote from this axis. These shear forces at the displaced interface would have to be compensated by greater free energy of chemical bonding to achieve the same ligand-receptor affinity as an on-axis interface. Second, a kinetic advantage arises because an interface at a peripheral position will be moving faster than an interface at an axial position (on average, in the center-of-mass inertial frame, which is most relevant to encounter complexes). As a ligand begins to dissociate from the interface, the same angular movement of the receptor will in the peripheral case cause a greater linear separation of contact residues. This greater linear separation will stretch receptor-ligand bonds to a greater extent, making the ligand more likely to dislodge.

Figure 6.

On-axis vs. off-axis binding of a ligand to a receptor. The cylinder represents a hypothetical receptor. Spheres represent a ligand binding to a site on the receptor's principal axis (Right) or on the periphery (Left). Dashed lines represent an angular displacement of the receptor ligand-binding sites because of a rocking motion of the receptor. Stretched hydrogen bonds illustrate that the same angular displacement leads to a much greater linear translation of the off-axis ligand-binding site, as discussed in the text.

Abbreviations

TCR

T cell antigen receptor

CDR

complementarity-determining region

H1

H2, H3, L1, L2, L3, CDRs 1, 2, 3 of heavy and light chains

MHC

major histocompatibility complex

PDB

Protein Data Bank

Fv

heterodimer of V_H and V_L