A Mathematical Model for Comparison of Bolus Injection, Continuous Infusion, and Liposomal Delivery of Doxorubicin to Tumor Cells

Abstract

Determining the optimal mode of delivery for doxorubicin is important given the wide use of the drug against many tumor types. The relative performances of bolus injection, continuous infusion, liposomal and thermoliposomal delivery are not yet definitely established from clinical trials. Here, a mathematical model is used to compare bolus injection, continuous infusion for various durations, liposomal and thermoliposomal delivery of doxorubicin. Effects of the relatively slow rate, and saturability, of doxorubicin uptake by cells are included. Peak concentrations attained in tumor cells are predicted and used as a measure of antitumor effectiveness. To measure toxicity, plasma area under the curve (AUC) and peak plasma concentrations of free doxorubicin are computed. For continuous infusion, the duration of infusion significantly affects predicted outcome. The optimal infusion duration increases with dose, and is in the range 1 to 3 hours at typical doses. The simulations suggest that continuous infusion for optimal durations is superior to the other protocols. Nonthermosensitive liposomes approach the efficacy of continuous infusion only if they release drug at optimal rates. Predictions for thermosensitive liposomes indicate a potential advantage at some doses, but only if hyperthermia is applied locally so that the blood is not significantly heated.

Introduction

Doxorubicin (adriamycin) is one of the most commonly used anticancer drugs. When it was first introduced, bolus intravenous injection was the only mode of delivery. The effectiveness of doxorubicin against many tumors is offset by its cardiotoxicity, which limits the lifetime dose a patient may receive per unit body surface area to around 450 to 550 mg/m² [1,2]. More recently, fractionated schedules of administration, continuous infusion, liposomal, and thermoliposomal delivery were developed in an attempt to reduce toxicity to the heart and other normal tissues, while retaining the antitumor effects. Rational criteria for choosing among these various therapeutic modalities are lacking at present.

In a recent review, de Valeriola [3] states that optimal dosage regimens for anthracycline drugs (including doxorubicin) have yet to be determined, and that although cardiotoxicity has been reduced by fractionated doses or continuous infusion, there is insufficient data to conclude that these schedules give antitumor response equivalent to that from bolus injection. The studies of Legha et al. [4], Abraham et al. [5], and Hortobagyi et al. [6], which found essentially the same clinical outcomes for continuous infusion and bolus injection, led Doroshow [7] to conclude that “there is little evidence that changes in schedule make any significant difference as far as antitumor activity.” However, these studies used infusion times only in the range 24 to 96 hours. The possibility that shorter infusion times might give altered outcome was therefore not explored. Casper et al. [8] reported significantly lower fatal outcome from disease for patients with sarcoma treated with bolus injection compared with continuous infusion. Muller et al. [9] compared continuous infusion over 96 hours with bolus administration in patients with leukemia, for similar total exposure (AUC, or area under the concentration-time curve). They found a cellular AUC 2.85 times greater for bolus injection, and a peak cellular concentration three times higher. The issue of whether continuous infusion is more favorable is therefore not settled.

Injection of doxorubicin encapsulated in liposomes was developed as an alternative to intravenous injection of free doxorubicin. Liposomal delivery offers a possible means of reducing systemic exposure relative to tumor exposure, by exploiting the preferential extravasation of liposomes out of tumor rather than normal microvessels [10]. Liposomes with polyethylene (“PEG”) coating have much longer plasma half-lives, which appears advantageous. Some animal studies of liposomal doxorubicin are promising [11–13]. Storm et al. [11] found liposomal doxorubicin to be superior to bolus injection in a rat model, although no increase in therapeutic benefit from continuous infusion was seen. To date, liposomal preparations have been shown conclusively to be clinically superior to other treatments only for AIDS-associated Kaposi's sarcoma [14]. Muggia et al. [15] found that liposomal doxorubicin had activity against refractory ovarian cancer, but a controlled comparison with free doxorubicin was not made. Liposomally encapsulated doxorubicin has decreased cardiotoxocity and nephrotoxicity, but liposomes are taken up by macrophages in the liver, resulting in an altered form of dose-limiting toxicity [16].

Thermosensitive liposomes (thermoliposomes) have been developed [17–20] to take advantage of increased tumor and cellular uptake of doxorubicin on heating [17,21], as well as possible enhanced cell kill from simultaneous exposure to doxorubicin and heat [21,22]. This allows the option of applying heat locally rather than to the entire body. Studies assessing the clinical benefit of thermoliposomes have yet to be performed. No quantitative predictions for the improved delivery with hyperthermia have been made, so that the rational basis for use of thermoliposomes is still uncertain.

Consideration of transport issues suggests that the different treatment modalities discussed above should be expected to give significantly different outcome. Under clinical conditions, the primary means of lethal action of doxorubicin appears to be inhibition of topoisomerase-II, and the preponderance of evidence suggests that the drug must enter the cells to be toxic [23]. To kill a tumor cell, doxorubicin in circulation must cross vessel walls, travel to the tumor cells, cross the cell membranes, and then enter the cell nucleus. While these transport processes are occurring, drug also reaches normal tissues, and clears from the circulation. Once drug begins to clear from the blood, free drug (not bound or sequestered within the cells) starts to clear from the tumor also. Although the initial half-life of doxorubicin has been measured as 4.75 minutes [24], cellular pharmacokinetic studies of doxorubicin show time-scales of hours for equilibration of doxorubicin concentration inside and outside cells [25–29]. This suggests that much of the injected drug clears before it can enter tumor cells. Thus, cellular drug exposure may not be proportional to plasma exposure. Different schedules of delivery giving the same plasma AUC may give different cellular exposure, whether measured as cellular AUC or peak drug concentrations. Moreover, both toxicity and tumor cell kill can show nonlinear dependence on drug exposure [1,29], suggesting that optimization of dosage and other factors can have a significant effect on outcome. Given the many variables involved, mathematical models that can account for the abovementioned transport processes in comparing different treatments may be useful.

Previous pharmacokinetic modeling for doxorubicin (e.g., Ref. [30]) has aimed mainly at predicting plasma concentration, on the assumption that plasma concentration is a good predictor of antitumor effect. However, as noted above, tumor concentrations often do not correlate directly with plasma concentrations [31]. Chan et al. [32] and Chen and Gross [33] allowed for a separate tumor compartment. Swan [34,35] used mathematical modeling to determine the optimal rate of delivery of a general drug, accounting for tumor growth kinetics, but this rate is for drug at the tumor site, and gives no information on how this rate is achieved by some feasible procedure of intravenous delivery. None of these mathematical models compared bolus injection or continuous infusion with liposomal delivery. A limitation of all these models is that they do not distinguish between extracellular and intracellular drug within the tumor.

The modeling studies of Tsuchihashi et al. [36] and Harashima et al. [37] addressed the issue of optimizing liposomal release kinetics. Their model contains an intracellular compartment. However, their criterion for optimization is maximizing tumor cell kill, with the assumption that the rate of tumor cell kill is linear in the concentration of free doxorubicin in the extracellular space. This neglects the saturability of transmembrane transport, and is based on cell kill being dependent on AUC. Harashima et al. [37] justify this as being appropriate for cell cycle phase-nonspecific drugs. It will be shown later in this paper that saturability of extra- to intracellular transport, far from being negligible, is the most significant factor determining delivery to the cell interiors.

The assumption of Tsuchihashi et al. [36] and Harashima et al. [37] that doxorubicin cellular AUC determines cell kill has a major effect on their conclusions about optimal release kinetics. However, studies at the cellular level suggest that peak levels rather than AUC are more important in determining cytotoxicity. The strongest evidence for this is data of Durand and Olive [25], who exposed mouse and Chinese hamster fibroblasts for a range of durations up to 6 hours, at several different extracellular concentrations. The surviving fraction for all these experiments could be plotted on a single curve versus the intracellular doxorubicin concentration at the time the incubation was terminated (which is also the peak intracellular concentration). This apparent independence from time of exposure is consistent with peak cellular concentration determining cytotoxicity. If cellular AUC determined cytotoxicity, these data could not coincide on one curve. Further evidence of the importance of peak concentrations is given by Nguyen-Ngoc et al. [38], who studied mouse sarcoma cells in culture. For similar total exposures (AUC for extracellular concentration), high extracellular concentration for a short time was found to give higher cytotoxicity than low extracellular concentration for a long time. The data of Morjani et al. [39] for human leukemic cells also contradicts the assumption that cytotoxicity depends primarily on nuclear AUC. In the models developed in this paper, peak intracellular concentrations, rather than cellular AUC, are used as a measure of tumor cell kill.

In this study, mathematical models for comparing bolus injection, continuous infusion, and liposomal delivery of doxorubicin are developed. Time-dependent plasma clearance, drug extravasation and diffusion, and drug transport across the cell membrane are taken into account. Saturability of the transmembrane transport is included. The relative performances of different treatment modalities, schedules, and dosages are assessed by predicting three indices: peak intracellular drug concentration in the tumor (a measure of fractional tumor cell kill); plasma AUC; and peak plasma concentration. Plasma AUC correlates with the dose-limiting toxicities for a single cycle (generally due to myelosuppression, hematological toxicities, or mucositis [40]). Peak plasma concentration correlates with cardiotoxicity [3–5,40,41], the cumulative dose-limiting toxicity for multiple cycles. The use of tumor intracellular concentration, rather than plasma or total tumor (intracellular plus extracellular) concentration, to measure antitumor efficacy is a key feature of the models. The predictions are used to quantitatively assess whether various features of liposomes and thermoliposomes that are generally assumed to result in advantageous delivery (e.g., selective uptake in the tumor, increased uptake on heating) can in fact be expected to have a significant effect.

Materials and Methods

The distribution of drug in a tumor is represented in terms of its concentrations in three compartments: intracellular, c_i (t); extracellular, c_e(t); and vascular (plasma), c_v(t). Doxorubicin binds extensively to proteins in both the plasma and tissue [7]; c_e(t) and c_v(t) therefore represent only protein-unbound drug. The following system of ordinary differential equations is solved over time t

$$\frac{d{c}_{\text{i}}}{dt}=V_{\max }\left(\frac{c_{\text{e}}}{c_{\text{e}}+K_{\text{e}}\phi }-\frac{c_{\text{i}}}{c_{\text{i}}+K_{\text{i}}}\right),$$ 1

$$\frac{d{c}_{\text{e}}}{dt}=P{S}_{\text{t}}\left(c_{\text{v}}-c_{\text{e}}\right)-d_{\text{c}}{V}_{\max }\left(\frac{c_{\text{e}}}{c_{\text{e}}+K_{\text{e}}\phi }-\frac{c_{\text{i}}}{c_{\text{i}}+K_{\text{i}}}\right)$$ 2

Here, c_i is expressed in units of nanograms per 10⁵ cells, and c_e is expressed as milligrams per milliliter extracellular space. The parameters appearing in these equations are defined in Table 1, which also shows the assumed values. The first term on the right hand side of Equation 2 represents diffusive transport across microvessel walls. Convective transport may also contribute to transvascular exchange. However, the rate of convective flow in tumors is believed to be low due to high interstitial fluid pressure [42], and so its effect on transport is neglected here. The vessels are modeled as a distributed source, which is equivalent to neglecting gradients of concentration between microvessels. This assumption is justified when the dimensionless quantity PL²S_t/(4D_t) (parameters defined in Table 1) is small relative to 1 [31]. In the present case, PL²S_t/(4D_t)≈0.1.

Table 1.

Model Parameters.

Symbol	Description	Value	Source
MW	molecular weight of doxorubicin	544	-
L	typical spacing between microvessels in tumor	200 µm	[64]
Dt	diffusivity of doxorubicin in tumor	1.6x10-6 cm/s2	[65] correlation with MW=544
D	total dose of doxorubicin injected	100–285 mg (free), 20–350 mg (liposomal)	see text
St	vascular (suraface) density in tumor	200 cm-1	[42]
P	tumor vascular permeability for doxorubicin	1.0x10-4 cm/s	[67]: value for sulforhodamine (MW=558) in granulating tissue is 3.4x10-5 cm/s; assume tumor value is three times greater (cf. albumin data)
VB	total blood volume in body	5.0 l	[68]
Vt	total tumor volume	50 ml	(assumed)
dc	cell density	6x108 cells/ml	assumes φ=0.4; cell volume 10-9 cm3 [44]
φ	volume fraction of extracellular space (tumor)	0.4	[66]
$$t_{1/2}^{\alpha }$$	initial plasma half-life of doxorubicin	4.75 min	[24]
α	time constant for doxorubicin in plasma	0.693/$t_{1/2}^{\alpha }$	[24]
A	inverse volume of distribution in plasma	0.13/l	[24]
Vmax	rate constant in kinetics for cellular transmembrane transport	0.28 ng/(105 cells)/min	fit to data from [29]
Ke	Michaelis constant for cellular transmembrane transport	0.219 µg/ml	fit to data from [29]
Ki	Michaelis constant for cellular transmembrane transport	1.37 ng/(105 cells)	fit to data from [29]
PL, $P_{\text{L}}^0$	tumor vascular permeability of liposomes	3.4x10-7 cm/s	[67]
td	duration of hyperthermia	60 min	[17]
th	time after injection when hyperthermia starts	120 min	[18]
E	enhancement factor for PL at 45°C	1–100	[17]
A1	plasma pharmacokinetic parameter for liposomes	6.9 µg/ml	[53]
A2	plasma pharmacokinetic parameter for liposomes	12.2 µg/ml	[53]
k1	plasma pharmacokinetic parameter for liposomes	0.00502 min-1	[53]
k2	plasma pharmacokinetic parameter for liposomes	0.00025 min-1	[53]
DG	dose corresponding to A1, A2, k1, k2	50 mg/m2	[53]
τre, ${\tau }_{\text{re}}^0$	time constant for liposome rupture in tumor extracellular space	24 h	[18] (see text)
$${\tau }_{\text{re}}^{\text{h}}$$	time constant for liposome rupture in tumor extracellular space at 45°C	0.72 min	[19]
τrv, ${\tau }_{\text{rv}}^{\text{0}}$	time constant for liposome rupture in plasma	24 h	[18] (see text)
$${\tau }_{\text{rv}}^{\text{h}}$$	time constant for liposome rupture in plasma at 45°C	0.72 min	[19]

Doxorubicin is believed to be transported passively across the cell membrane [26]. For some cells efflux may be a combination of passive and active transport, especially for resistant cells where there is evidence that p-glycoprotein is associated with increased doxorubicin efflux [7]. The expression in Equation 1 for cellular uptake of doxorubicin is similar to that given by Friedman [43] for passive carrier-mediated transmembrane transport, and is a simple form that can fit cellular uptake rate data that shows saturation in both intracellular and extracellular concentrations. This type of saturation is seen in the time-dependent uptake data of Kerr et al. [29] for non-small cell lung tumor cells that were not selected to be resistant. (The concentration c_e is the concentration of the incubating medium and therefore corresponds in tissue to amount of doxorubicin per volume of extracellular space.) The parameters V_max, K_e, and K_i (Table 1) are chosen to fit data in Fig. 2 of Kerr et al. [29]. To compare K_e (in units of micrograms per milliliter) and K_i, (in nanograms per 10⁵ cells), a typical cell volume of 10^-9 ml is assumed, based on typical dimensions of 10 µm for lung cells [44]. Then from the fitted values, K_i/K_e≈60, implying that the intracellular concentration is much larger than the extracellular concentration at equilibrium. This is attributed to binding to intracellular sites or storage in intracellular compartments, and is consistent with other studies showing ratios of intra- to extracellular concentrations in the range 30 to 1000 [7]. The cell density is d_c=10⁹ (1 - φ) cells/ml, based on the assumed cell volume of 10^-9 ml, where φ is the extracellular volume fraction.

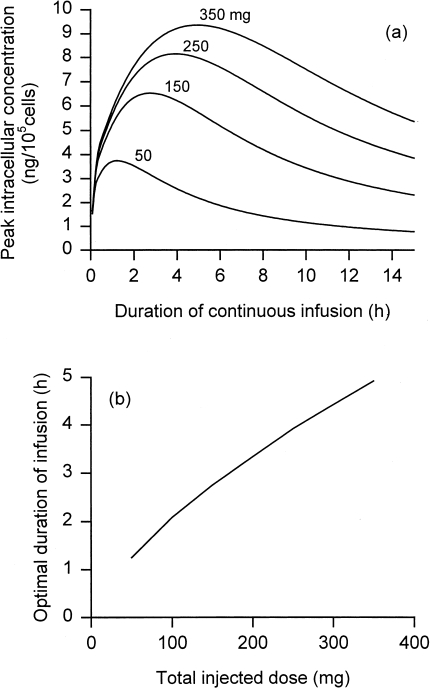
Figure 2.

(a) Peak intracellular concentration achieved in tumor as a function of duration of continuous infusion of doxorubicin, for indicated total injected doses. (b) Optimal duration of continuous infusion as a function of total injected dose. Parameters as in Table 1.

The (initial) half-life of doxorubicin in plasma was measured as $t_{1/2}^{\alpha }=4.75$ minutes by Robert et al. [24] for a population of patients with breast cancer. They found plasma concentration for an infusion time T to be governed by

$$c_{\text{v}}(t)=\frac{D}{T}\left[\frac{A}{\alpha }(1-{\text{e}}^{\text{-}\alpha t})+\frac{B}{\beta }(1-{\text{e}}^{\text{-}\beta t})+\frac{C}{\gamma }(1-{\text{e}}^{\text{-}\gamma t})\right],$$ 3

for t<T and

$$\begin{array}{l}{c}_{\text{v}}(t)=\frac{D}{T}[\frac{A}{\alpha }({\text{e}}^{\alpha T}-1){\text{e}}^{\text{-}\alpha t}\\ +\frac{B}{\beta }({\text{e}}^{\beta T}-1){\text{e}}^{\text{-}\beta t}+\frac{C}{\gamma }({\text{e}}^{\gamma T}-1){\text{e}}^{\text{-}\gamma t}]\end{array}$$ 4

for t>T. Here, D is the total dose injected, α=0.693/$t_{1/2}^{\alpha }$, and the parameter A was measured in the range 0.0157 to 0.13/I (individual variation). Values for the other pharmacokinetic parameters β, γ, B, and C are given in their paper; the terms involving these parameters represent the compartments with much slower elimination, and are neglected here (see below). Plasma concentration c_v(t) for bolus injection is then given by

$$c_{\text{v}}(t)=\frac{D}{T}\left[\frac{A}{\alpha }({\text{e}}^{\alpha T}-1){\text{e}}^{\text{-}\alpha t}+\frac{B}{\beta }({\text{e}}^{\beta T}-1){\text{e}}^{\text{-}\beta t}+\frac{C}{\gamma }({\text{e}}^{\gamma T}-1){\text{e}}^{\text{-}\gamma t}\right],$$ 5

The plasma AUC (area under the curve) for both cases (after neglect of terms) is DA/α. Doroshow [7] states that clearance (of unencapsulated doxorubicin) is independent of dose, justifying the use of these forms, which are linearly scaled with dose D.

The neglected terms in Equations 3 and 4 (involving B and C) come from the (β and γ phases (long-time tails). The terminal half-life of 30 to 50 hours may give over 70% of the total plasma AUC [7]. However, for predicting peak concentrations, only the initial half-life is relevant, because concentrations after this initial decay are much smaller. Even if it were of interest to maximize cellular AUC rather than cellular peak concentration, it is only necessary to consider time periods when plasma (and therefore tumor extracellular) concentration is high enough to saturate cellular influx. Only during this period will the schedule of drug infusion affect cellular AUC. This justifies the neglect of the long-time tails for the analysis here.

In Equations 1 and 2, c_e and c_i are assumed to be uniform across the entire tumor. Given the diffusivity of doxorubicin (Table 1), this assumption is valid if microvessels are typically spaced around 200 microns or less, because time scales for the other transport steps are longer (Table 2). However, if the tumor has regions that are poorly vascularized (with regions where spacing between microvessels is much greater than 200 µm), spatial gradients of drug concentration may become significant. The effect of these spatial variations will be considered in a future study. The present analysis is limited to reasonably well-vascularized tumors. Such tumors appear to be the most likely to respond to chemotherapy [45–47].

Table 2.

Time Scales Involved in Transport of Circulating Doxorubicin to Tumor Cell Interiors.

Transport step	Timescale	Value	Comments
Clearance from plasma	τ	4.8 min	[24]
Crossing microvascular wall	1/(StP)	50 s	Assumes St=200 cm-1
		8.3 min	Assumes St= 20 cm-1 (poorly vascularized)
Diffusing in extracellular space to	L2/Dt	1 min	Assumes L= 100 µm
regions distant from microvessels		26 min	Assumes L=500 µm (poorly vascularized)
Crossing cell membrane		3–6 hours	[25–29]

See Table 1 for parameter definitions and values.

The parameter D in this model, the total amount of doxorubicin injected in a single therapy cycle, is limited by myelosuppression and leukopenia to around 60 to 75 mg/m² [4]. Therapy cycles are normally separated by at least a week, so that residual drug from a previous cycle is too small to affect the next cycle. Cardiotoxicity limits the cumulative dose from multiple cycles to around 500 mg/m² for bolus injection, but with continuous infusion, some patients have tolerated cumulative doses up to 700 mg/m² [4]. The recent development of high-dose chemotherapy protocols, where chemotherapy is combined with bone marrow rescue, have allowed as high a dose per cycle as 110 mg/m² for multiple cycles [48], and 165 mg/m² for a single cycle [49]. Assuming an average body surface area of 1.73 m² [50], this gives a range for D of 100 to 285 mg.

Equations 1 and 2 were integrated in time using a fourth-order Runge-Kutta scheme [51]. Initially, doxorubicin concentration is zero in both the extracellular and intracellular spaces. Time steps of 0.01 minutes gave results sufficiently close to results with smaller time steps, and were therefore used.

The analysis for the case of doxorubicin encapsulated in liposomes is now formulated. Intravenously injected liposomes are assumed to extravasate selectively in the tumor, and to release their contents in the extracellular space. Extravasation in nontumor tissues is neglected. Liposomes cannot penetrate into tissue further than the immediate perivascular area [52], so their concentration in the tumor compartment is nonuniform. However, diffusion of free doxorubicin over the typical distance between vessels is rapid relative to the rates of uptake by vessels and cells (Table 2), and also relative to the timescale for release of drug from the liposomes. Therefore, the concentration of free doxorubicin is well approximated as uniform, and moreover, taking into account the nonuniform concentration of liposomal doxorubicin would make negligible difference to the calculations. Consequently, spatial variations in both unencapsulated and liposomal doxorubicin concentration between microvessels are neglected.

Only free doxorubicin can enter the tumor cells and kill them. Therefore, the concentrations of free and liposomally encapsulated doxorubicin must be distinguished. The variables are: c_i, c_e, and c_v, the concentrations of free doxorubicin in the intracellular, extracellular, and vascular compartments, respectively; and c_Lv, c_Le, the concentrations of encapsulated doxorubicin in the vascular and extracellular compartments, respectively. The first three have the same units as above; c_Lv has units of micrograms per milliliter of plasma, and C_Le is in micrograms per milliliter of total tissue.

The equation used for liposomal doxorubicin in the plasma is a biexponential fit made by Gabizon et al. [53] to their clinical data:

$$c_{\text{Lv}}(t)=\frac{D}{D_{\text{G}}}\left[A_1{\text{e}}^{\text{-}{k}_{1}t}+A_2{\text{e}}^{\text{-}{k}_{2}t}\right],$$ 6

(see Table 1), where the factor D/D_G scales linearly for doses D other than the dose D_G they used. Their total dose (of encapsulated doxorubicin) was 50 mg/m²; as before an average body surface area of 1.73 m² is used [50] to obtain D_G=86.5 mg. Equation 6 is for nonthermosensitive liposomes coated with polyethylene glycol (“PEG”). PEG-coated liposomes have slower plasma clearance than uncoated liposomes [12,53,54]. Current clinical trials have focused on PEG-coated liposomes, and for this reason, only this type is modeled here. Equation 6 is used here for thermosensitive liposomes as well, because they are of similar size and also PEG-coated.

For liposomal doxorubicin in the extracellular space,

$$\frac{d{c}_{\text{Le}}}{dt}=P_{\text{L}}{S}_{\text{t}}\left(c_{\text{Lv}}-c_{\text{Le}}\right)-\frac{c_{\text{Le}}}{{\tau }_{\text{re}}},$$ 7

where the first term accounts for transvascular transport and the second for release of free doxorubicin from liposomes within the extracellular space. The equations for intracellular and extracellular free (unencapsulated) doxorubicin (c_i and c_e) are the same as (1) and (2), except that a third term, c_Le/τ_re, is added to the right-hand side of Equation 2 to represent release of doxorubicin from liposomes. As before, c_e and c_v (the plasma concentration of unencapsulated doxorubicin) are for protein-unbound drug. Although the amount of free doxorubicin in the plasma is initially zero, over time the circulating liposomes release doxorubicin, and the doxorubicin released in the extracellular spaces can diffuse back into the plasma. Therefore, the plasma concentration of free doxorubicin c_v is governed by

$$\frac{d{c}_{\text{Le}}}{dt}=P_{\text{L}}{S}_{\text{t}}\left(c_{\text{Lv}}-c_{\text{Le}}\right)-\frac{c_{\text{Le}}}{{\tau }_{\text{re}}},$$ 8

where the first term accounts for transvascular transport, the second is due to doxorubicin released from circulating liposomes, and the third is due to clearance of free doxorubicin from the plasma (by excretion in other organs of the body). V_t and V_B are the tumor and blood volumes, respectively. The factor (V_t/V_B) S_t is essentially a conversion from amount of drug per unit volume of tumor, to amount per unit volume of plasma. The factor AV_B, which uses the volume of distribution parameter determined by Robert et al. [24], corrects for the fact that when doxorubicin is released by liposomes into the plasma, not all of it becomes available as protein-unbound drug. Because the drug is released only in the extracellular spaces of the tumor, some drug is lost to surrounding normal tissue by diffusion and convection; this is neglected here. Because doxorubicin diffuses across 0.5 cm on a timescale of 3.6 hours (from the value of D_t, Table 1), loss to surrounding tissue by diffusion is not expected to be a major effect, except for extremely small tumor nodules.

The kinetics of drug release from liposomes can be manipulated [55,56]. Clinical trials of liposomal doxorubicin have used different preparations and unfortunately data on the kinetics of drug release from these preparations are not reported. Gabizon et al. [53] give pharmacokinetic fits to both the total doxorubicin and liposomal doxorubicin in plasma, from which it can be seen that the rate of release of drug from the liposomes in plasma for their particular preparation is very slow. It is also not known whether release of doxorubicin from liposomes occurs at the same rate in plasma as in the tissue extracellular spaces. The possibility that tumor-associated macrophages might take up liposomes and release doxorubicin has been investigated and found to be insignificant [57]. Factors such as pH that may differ between tumor and plasma may affect doxorubicin release, but in the absence of any data on this, the assumption is made here that the release follows first-order kinetics with a rate-constant that is the same in plasma and tumor extracellular space. An exception is the case of thermoliposomes, which release their contents within minutes on heating [19]. Zou et al. [18], who observed continuing increases of doxorubicin concentration in tissue over a period of 24 or more hours, attributed this increase to “drug leakage from liposomes retained in the tumor vasculature into the tumor cell compartment.” Because hyperthermia was applied at 2 hours, this presumably reflects drug release primarily in the absence of heat. This is the basis for an assumed time constant of doxorubicin release of 24 hours (Table 1), for what are here termed “slow-release” liposomes. As noted by Lim et al. [56], “Liposome formulations… traditionally focused on lipid concentrations that exhibit decreased plasma elimination rates and slow drug release rates.” Thus preparations used up until now in clinical trials are represented by this “slow-release” case. However, because the time constant for drug release can be manipulated, this time constant is also taken as a parameter to be optimized in the analysis below.

Initial conditions for the system of equations are c_Le=c_v=c_e=c_i=0. Although liposomal delivery appears to reduce cardiotoxicity, myelosuppression still limits the dose D that can be administered on a single cycle. Moreover, macrophage uptake of liposomes in the liver [16] also causes toxicity. Clinical studies with humans have used doses for single-therapy cycles of 10 to 80 [58], 10 to 50 [10], 30 to 50 [59], and 25 to 50 mg/m² [53]. Daemen et al. [16] used doses of 5 mg/kg in rats, which, for a 70 kg human would correspond to 350 mg. However, rats generally tolerate higher doses than humans. Doses in the range D=50 to 350 mg are assumed here. The equations are solved numerically as already described.

The above model for liposomes is now adapted to thermosensitive liposomes (thermoliposomes), which are designed to release their contents rapidly on heating [18,19]. Apart from its effect on release kinetics of doxorubicin from thermoliposomes, hyperthermia increases the tumor vascular permeability to liposomes. Several studies have found that it increases drug influx into cells [21,60], although one study was far less conclusive in finding enhanced doxorubicin-induced cytotoxicity to cells also exposed to heat [61]. Because of lack of quantitative data, the effects of heat on cytotoxicity and drug influx are not included in this study, which analyzes only the other transport effects of heat. Drug delivery by thermoliposomes is modeled with Equations 1 and 2 as modified, (6) to (8), with two changes. Firstly, τ_re, the time constant for release of doxorubicin from the liposomes in the tumor extracellular space, is replaced by the following function of time:

$${\tau }_{\text{re}}(t)=\{\begin{array}{l}{\tau }_{\text{re}}^{\text{0}}\text{if}t\text{<}{t}_{\text{h}}\text{or}t\text{>}{t}_{\text{h}}+t_{\text{d}}\\ {\tau }_{\text{re}}^{\text{h}}\text{if}{t}_{\text{h}}\text{<}t\text{<}{t}_{\text{h}}+t_{\text{d}};\end{array}$$ 9

to reflect the change in kinetics of release on heating. Here, t_h is the time at which hyperthermia is begun, and t_d is the duration of hyperthermia. Zou et al. [18] in their animal experiments applied hyperthermia starting 2 hours after initial injection, so that t_h=2 hours is used here. Gaber et al. [17] sustained heating for 1 hour in their rat experiments, and this value for t_d was used here. It takes around 5 minutes for tissue to reach the target temperature [19]; because this is short relative to t_d, transients due to this startup time are neglected. The time constant${\tau }_{\text{re}}^{\text{h}}$ for release of doxorubicin from liposomes under hyperthermia (45°) is determined from Wu et al. [19], who note that at this temperature the liposomes release 10% of their contents after 100 seconds. This implies${\tau }_{\text{re}}^{\text{h}}$=0.72 minutes. Secondly, the permeability of the vessel to liposomes is assumed to increase during heating, so that the parameter P_L is replaced by a function of time:

$$P_{\text{L}}(t)=\{\begin{array}{l}{P}_{\text{L}}^{\text{0}}\text{if}t\text{<}{t}_{\text{h}}\text{or}t\text{>}{t}_{\text{h}}+t_{\text{d}}\\ E{P}_{\text{L}}^{\text{0}}\text{if}{t}_{\text{h}}\text{<}t\text{<}{t}_{\text{h}}+t_{\text{d}};\end{array}$$ 10

where E is an enhancement factor. Gaber et al. [17] observed a 76-fold increase in liposome extravasation on heating to 45°C. It is difficult to deduce from this the increase in the value of P_L itself. The range of E=1 to 100 is considered here.

Wu et al. [19] argue that release of doxorubicin from circulating thermoliposomes into the plasma on heating is negligible in their experiments, based on the short residence time of blood in the tumor. This is the “idealized” case of local heating: the time constant of release from liposomes in the plasma τ_rv remains constant, whereas the time constant for release in the tumor extracellular space τ_re is greatly decreased (to ${\tau }_{\text{re}}^{\text{h}}$). On the opposite extreme, if the blood temperature equilibrates to the temperature of the heated region, τ_rv will also become much smaller. For a human patient, the actual situation is probably between these two extremes, depending on how large a portion of the body is heated. Both “idealized” local heating and the case of heated blood (i.e., blood temperature equilibrated to the heated temperature) are modeled here. For the latter case, τ_rv is set equal to the function τ_re(t) given by Equation 9.

To relate peak intracellular concentration of doxorubicin to fractional cell kill, data of Kerr et al. [29] for human non-small cell lung cancer are used. For such cells in monolayer culture, Kerr et al. present a plot of surviving clonogenic cell fraction as a function of intracellular concentration. The intracellular drug concentration shown in their Fig. 6 is the peak level reached during the treatment, because it represents levels when the cells were removed from the incubating solution of drug.

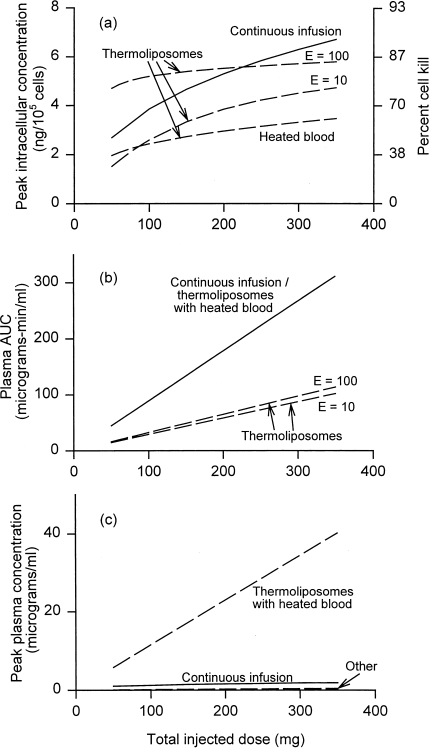
Figure 6.

Comparison of drug delivery and toxicity for thermoliposomes, and continuous infusion for the optimal duration (from Figure 1b). For thermoliposomes, three cases are shown: heated blood, and idealized local heating assuming the vascular permeability of liposomes is increased by a factor of 10 upon heating, or by a factor of 100. (a) Maximum tumor intracellular concentration. (b) Toxicity measured by plasma AUC. (c) Toxicity measured by peak plasma concentration. All as a function of total injected dose.

The plasma half-life of doxorubicin used here was measured for patients with breast cancer [24]. It mainly reflects the clearance by eliminating organs such as the liver and kidneys. Variations in plasma clearance rates due to tumor size (i.e., varying tumor uptake) are neglected. For a typical plasma concentration of 20 µg/ml, the total amount of drug initially in the circulation is 100 mg (assuming 5 l total blood volume). A typical peak extracellular drug concentration is 2 µg/ml, and a typical peak intracellular concentration is 10 ng/(10⁵ cells) or 60 µg/ml (using d_c from Table 1). Therefore the maximum total amount of drug in a 50-cm³ tumor is on the order of 3 mg. It is evident that clearance of the drug from the circulation is mainly due to eliminating organs and not to uptake by the tumor.

Results

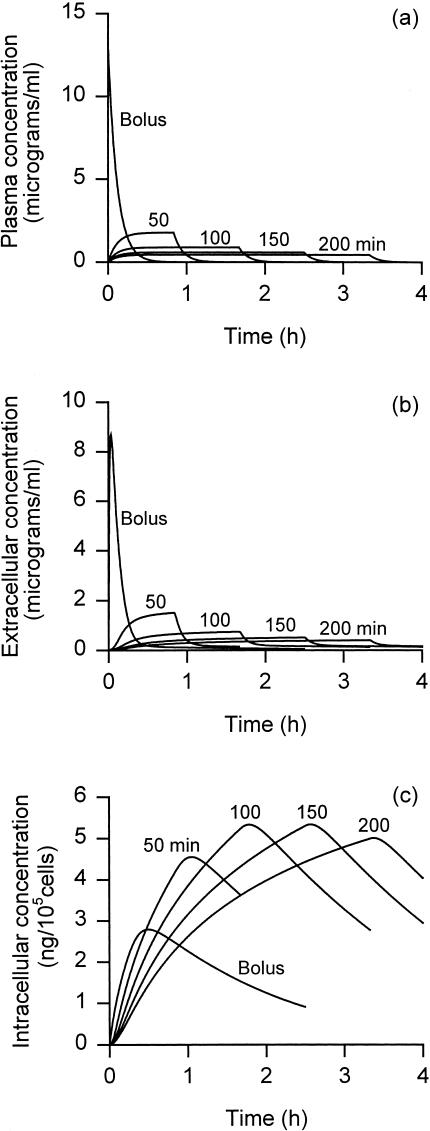
Figure 1 shows the predicted time course of plasma and intracellular doxorubicin concentrations, for a total dose of 100 mg administered by bolus injection and by continuous infusion (for durations 50–200 minutes). Intracellular concentration shows a time dependence very different from plasma concentration. Bolus injection gives an order of magnitude higher initial plasma level compared with continuous infusion (Figure 1a), but this leads to only a slight increase in the initial rate of cellular influx (initial slope of the curves in Figure 1b), as a consequence of saturation of cell uptake. The high plasma values achieved for a short time with bolus injection are therefore wasteful because their contribution to toxicity (plasma AUC and peak plasma levels) is substantial, but their effect on tumor cell kill is minor. The peak intracellular concentration initially increases with increasing duration of infusion, but then decreases.

Figure 1.

Concentrations of doxorubicin in (a) plasma, (b) tumor extracellular space, and (c) tumor intracellular space as a function of time after start of treatment, for bolus injection, and continuous infusion for indicated durations. Total injected dose 100 mg.

Figure 2a shows the peak intracellular concentration of doxorubicin achieved with continuous infusion, for several total injected doses, as a function of infusion duration. The duration of infusion has a significant effect on the amount of drug delivered to the cell interior. Continuous infusion is normally administered over 48 to 96 hours. From Figure 2a, such infusion durations result in much lower intracellular concentrations than could be achieved with shorter durations. Shorter durations still give lower peak plasma concentrations compared with bolus injection and therefore less cardiotoxicity. The optimum infusion duration increases with dose, and is in the range 1 to 3 hours (Figure 2b).

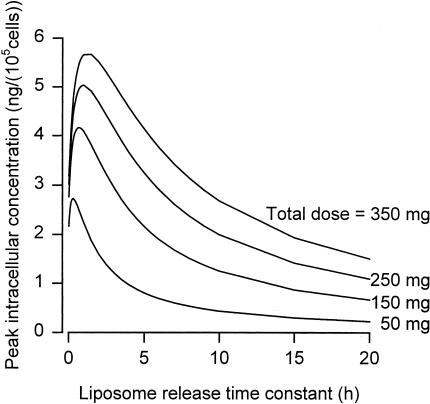
Figure 3 shows results for liposomes, with the time constant for release of doxorubicin from the liposomes (τ_re=τ_rv) varied. This parameter is analogous to the duration of continuous infusion. In fact, the liposomal case may be regarded as a continuous infusion directly in the extracellular tumor compartment, rather than the plasma compartment. As in the continuous infusion case, for each dose, peak intracellular concentration is maximized at a particular value of τ_re=τ_rv. This optimum release rate is dose-dependent, and appears to be much faster than in formulations of liposomal doxorubicin used in clinical trials so far.

Figure 3.

Peak intracellular concentration as function of the time constant for release of drug from the liposomes, for indicated total injected doses. Other parameters as in Table 1.

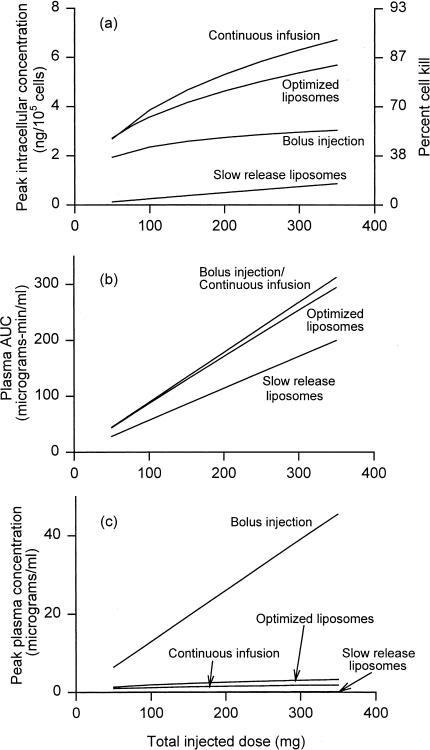
Drug delivery and toxicity resulting from several delivery modes are shown in Figure 4 as functions of total injected dose. The duration of continuous infusion at each dose is chosen to maximize peak intracellular drug concentrations (Figure 2b). With this choice, continuous infusion is significantly more effective than bolus injection (Figure 4a), while giving comparable or less toxicity. Figure 4b shows that toxicity that correlates with plasma AUC (such as myelosuppression) is identical in both cases. Figure 4c, however, shows the much lower peak plasma concentration for continuous infusion, which, as discussed earlier, is believed to be associated with reduced cardiotoxicity.

Figure 4.

Comparison of drug delivery and toxicity for various delivery modes: bolus injection, continuous infusion for the optimal duration (from Figure 1b), and liposomal delivery. Both slow-release liposomes (time constant 24 hours) and optimized liposomes (time constant for release varying with dose, less than 3 hours) are shown. (a) Maximum tumor intracellular concentration. (b) Toxicity measured by plasma AUC. (c) Toxicity measured by peak plasma concentration. All as a function of total injected dose.

Figure 4 also compares continuous infusion with liposomal delivery. Two cases of liposomes are shown: “slow release,” for which τ_re=τ^rv=24 hours, and “optimized,” for which at each dose τ_re=τ_rv, is chosen to give the maximum peak intracellular concentration (cf. Figures 3). Slow-release liposomes offer reduced toxicity, but greatly reduced efficacy. Optimized liposomes are slightly less effective than continuous infusion, with comparable toxicity. It appears that release in the tumor extracellular space, rather than the plasma, whereas in principle advantageous, in reality makes little difference. The explanation is that the rate-limiting step is entering the cells, with transport from the plasma to the tumor extracellular space taking place relatively fast. The comparison might be quite different for drugs other than doxorubicin, if their concentrations equilibrate much faster across the cell membrane.

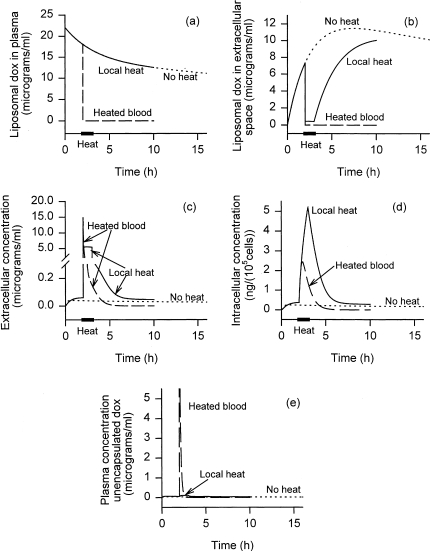
Figure 5 shows the time course of liposomally encapsulated doxorubicin concentration in the plasma and tumor extracellular spaces, as well as intracellular doxorubicin, for a 100-mg total dose of liposomal doxorubicin injected at time t=0. Three cases are shown: nonthermosensitive “slow-release” liposomes (without hyperthermia); thermosensitive liposomes with heated blood; and thermoliposomes with “idealized” local heating (no change in τ_rv), assuming the enhancement factor E=100 for liposomal vascular permeability. For nonthermosensitive “slow release” liposomes, the rate of release into the extracellular space is so low that extracellular concentrations are always low. Consequently, peak intracellular concentrations are low. Whereas the time constant for drug release from the “slow-release” liposomes was 24 hours in these simulations. Parr et al. [54] estimated a half-life of release of over 5 days for the liposomes they studied in mice. This much slower release would have resulted in even poorer results. This, along with Figure 4, shows the importance of optimizing liposomal drug release kinetics.

Figure 5.

Concentrations of (a) liposomally encapsulated doxorubicin in plasma, (b) liposomally encapsulated doxorubicin in the tumor extracellular space, (c) unencapsulated doxorubicin in the tumor extracellular space, (d) intracellular doxorubicin, and (e) unencapsulated doxorubicin in plasma as a function of time. Total injected dose 100 mg. For three cases: nonthermosensitive liposomes, thermoliposomes with heated blood, and thermoliposomes with “idealized” local heating, assuming enhancement factor of 100. Heating begins at 2 hours and lasts 1 hour.

For nonthermosensitive liposomes, in the case shown in Figure 5, plasma concentrations actually exceed tumor extracellular concentrations for the first 19 minutes. During this time, more doxorubicin reaches the tumor by leaking out of circulating liposomes and crossing the vessel wall as free drug, than by leaking out of liposomes that have extra-vasated into the tumor. By 19 minutes, the intracellular concentration reaches 78% of its maximal level. Thus, the original idea that liposomes would selectively extravasate into the tumor and leak drug into the tumor, with only a small amount clearing back into the plasma, is not borne out. Tumor extracellular concentration peaks at 39 minutes, and intracellular concentrations peak at 52 minutes. Liposomes remain circulating for hours after this, but have no more effect on peak cellular exposure.

For thermoliposomes in the “heated blood” case (for which the heated area is large enough so that the blood equilibrates to the elevated temperature), after initiation of hyperthermia all encapsulated doxorubicin in the plasma and tumor extracellular spaces is released very rapidly (Figure 5a and b). The doxorubicin suddenly released in the extracellular space (Figure 5c) is then available to enter the cells. For a short time, plasma concentration of free doxorubicin remains higher than the tumor extracellular concentrations, so that doxorubicin diffuses from the plasma into the tumor. As drug clears out of the plasma, however, within minutes the transvascular flux reverses direction, and doxorubicin begins to clear out of the extracellular space. This clearance is fast relative to cellular influx so that only a modest peak intracellular level is achieved (Figure 5d). This case is in fact nearly equivalent to bolus injection, because, as discussed earlier, the site of drug release is not very significant as long as the rate-limiting step is equilibration across the cell membrane.

With “idealized” local heating, the doxorubicin in the plasma remains encapsulated. There is a slightly faster decline in plasma levels of liposomal drug compared with the nonthermosensitive case (Figure 5a), because of the transient increase (by a factor E=100) in vascular permeability caused by hyperthermia. Heating also causes a much more rapid release of doxorubicin from the liposomes in the tumor extracellular space, explaining the dip in Figure 5b, lasting during the course of heating. After cessation of heating, tumor extracellular liposomal doxorubicin once again steadily accumulates due to extravasation (Figure 5b). However, because the rate of release after cessation of heat is slow compared with the rate of clearance back into the circulation, tumor extracellular free doxorubicin levels decline (Figure 5c). A decline in intracellular doxorubicin follows (Figure 5d).

It has been suggested that increased cellular uptake of doxorubicin with heat will lead to improved outcome when the drug is administered simultaneously with hyperthermia [21]. Equation 1 was fitted to data of Nagaoka et al. [21] for the temperatures 37, 39, 41, and 43°C. The fit suggested that the parameter K_i was virtually unchanged over these temperatures, but that the change in uptake was due to V_max increasing by a factor of 2.2. The simulations for thermoliposomes were performed again with V_max (from Table 1) multiplied by this factor, but K_i unchanged. The effect of this was negligible. This is attributed to the fact that K_i, the parameter determining at what concentration the cellular influx saturates, is the crucial parameter limiting uptake under in vivo conditions. It appears then that intervention strategies that increase uptake in vitro may not translate to increased delivery in vivo.

Some studies suggest that heat administered before exposure to doxorubicin will desensitize tumor cells to the drug [62], whereas simultaneous exposure to heat and doxorubicin gives enhanced cellular uptake of drug (presumably both in tumor and host cells). To investigate whether the delay time t_h between injection and heating has any effect on delivery, simulations were performed for various values of t_h. Only weak dependence of peak intracellular concentration on t_h was found, although values in the range 2 to 4 hours were found to be slightly better than much shorter or longer times. For all other simulations, the value t_h=2 hours (Table 1) was used.

Figure 6 compares drug delivery and toxicity for thermoliposomal delivery with the case of continuous infusion (for the optimal duration) already discussed. Figure 6a shows that thermoliposomes might give higher peak intracellular levels than continuous infusion at low doses, but only if hyperthermia increases liposome vascular permeability by at least two orders of magnitude (E=100). For high-dose chemotherapy, continuous infusion is comparable or superior. Thermosensitive liposomes with “idealized” local heating can be expected to give much lower cardiotoxicity, given the low peak plasma levels of free doxorubicin (Figure 6c), and they do give lower plasma AUC (Figure 6b). In reality, because tumors are likely to be disseminated, and the residence time of blood even in a single limb or other heated unit of the body is nonnegligible compared with the total circulation time through the body, the low plasma AUC of Figure 6b is unlikely to be achieved. Further, thermosensitive liposomes may still show dose-limiting liver toxicity due to uptake of whole liposomes by Kupffer cells. Therefore, although Figure 6 shows that thermoliposomes have a potential advantage over continuous infusion at lower doses, this advantage may be difficult to realize.

The effect of the enhancement factor E, which measures how much hyperthermia increases vascular permeability to liposomes, is also shown in Figure 6. For local heating, delivery depends strongly on E. For the heated blood case, the enhancement factor E gives no noticeable difference in delivery. This is because all liposomally encapsulated drug in the plasma is released within minutes after heating, after which the rate of liposome extravasation into the tumor becomes irrelevant.

Figures 4 and 6 show both the cost and the benefit of giving the maximum possible dose in a single cycle of therapy, based on the fractional cell kill percentages of Kerr et al. [29] (indicated on the axis). However, ever greater increases in dose are required to achieve each increment in fractional cell kill. For multiple therapy cycles, however, a small increase in fractional cell kill per cycle can have a substantial effect. Five cycles with 95% cell kill gives a surviving fraction of 3x10^-7 but with 97% cell kill the surviving fraction is one hundred times smaller. (Complete eradication of a tumor with, say, 5 billion cells requires a fractional cell survival of less than 2x10^-10.) This multiple-cycle effect becomes less significant as the single-cycle fractional cell kill decreases. These estimates are very approximate, because they do not take into account the increasing fraction of resistant cells on subsequent cycles, and the effect of tumor growth between cycles.

Given the uncertainty in experimental measurements of many of the parameters used in this model, as well as the possibility of wide interpatient variability, the sensitivity of the model to these parameters is of interest. The strongest sensitivity is to the cell pharmacokinetic parameters. Achieving extracellular concentrations much higher than the level of saturation is not useful because it does not result in faster transport. Thus, K_e or K_i, which are a measure of the concentration range at which saturation starts to slow transmembrane transport across the cell wall, are the most critical parameters for determining optimal time course for delivery. Changing these parameters would affect not only absolute levels of drug reached in the tumor cells, but also the relative performance of the various therapeutic modalities.

The parameter A, which is the inverse of a volume of distribution for the fastest-eliminating compartment in the plasma pharmacokinetic model of Robert et al. [24], has a significant effect on levels of intracellular drug reached for bolus injection or continuous infusion. This is expected because the plasma concentration is proportional to A. Robert et al. measured values from 0.0157 to 0.13/l, and the value 0.13/l was used in Figures 1–6. Smaller values of A are in fact equivalent to using a lower total dose D. For A=0.0157/l, the optimal durations of infusion are shorter (in the range 15–35 minutes) and show less dependence on dose. Peak levels of intracellular drug are roughly 40 to 60% of their values for A=0.13/l.

For bolus injection, increasing the half-life of doxorubicin in plasma results in more favorable delivery, at the expense of increased exposure (AUC). Some patients with cancer have impaired liver function as a result either of their disease or prior treatment. This can lead to a longer half-life of drug.

For liposomal doxorubicin, the assumption of Equation 6 that clearance is linear with dose is probably inaccurate. The results of Gabizon et al. [53] at two different doses suggest that clearance increases with dose. However, Allen [10] states that “The circulation half-life of small PEG-coated liposomes in humans is approximately 45 hours and is independent of dose.” An increase in plasma clearance reduces both the plasma AUC and the intracellular concentrations, but has little effect on comparison of peak intracellular concentration achieved at the same plasma AUC. Thus, the conclusions about performance of liposomal delivery relative to continuous infusion will not be affected by dose-dependent clearance.

Increasing vascular permeability P or P_L or increasing vascular surface density S_t results in faster delivery of drug from the circulation to the tumor, allowing higher extracellular concentrations. However, the drug also clears from the tumor faster, allowing less time for transport into the cell interiors. Because of these competing effects, there is an optimum value of the product PS_t or P_LS_t, which depends on the cellular pharmacokinetics. If S_t is decreased significantly, the above model may be inappropriate, because the diffusion of doxorubicin over the distance between microvessels may not be sufficiently rapid (cf. Table 2). Modeling the case of low S_t, such as occurs in poorly vascularized tumors, would require taking into account spatial variations of doxorubicin concentration between microvessels.

For liposomal delivery, increasing the tumor volume will increase the amount of free drug in plasma. Given Figures 4c and 6c, this will have a negligible effect on peak plasma concentrations, except for thermoliposomes when hyperthermia is not sufficiently localized. Figure 4b shows that plasma AUC for various cases of liposomal delivery is nonnegligible for the assumed tumor volume of 50 cm³. As tumor volume is increased the plasma AUC for all forms of liposomal delivery will increase, without any significant increase in tumor intracellular concentrations, making liposomal delivery more unfavorable.

Although this model represents a first step to rationally optimizing doxorubicin chemotherapy, it has a number of limitations, most notably the uncertainties in the cellular pharmacokinetic data.

Discussion

Table 2 shows the time scales for the various transport steps involved in the transport of drug from blood to the interior of tumor cells. Some of these values depend strongly on the microvascular permeability of doxorubicin, vascular surface density, and typical vessel spacing, all of which might vary from one tumor type to another. The rate-limiting step for doxorubicin, however, is transport across the cell membrane. Because of saturability of the kinetics of extra- to intracellular doxorubicin transport, there is a threshold beyond which increasing extracellular concentration in the tumor to a very high level results in negligible increase in intracellular drug levels. Because cellular influx is slow, extracellular concentrations must be sustained for a relatively long time to achieve significant transport of drug into the cell. This explains why continuous infusion can be more effective than bolus injection, for the same total injected dose and same plasma AUC. However, because intracellular concentration does not continually accumulate with time, but rather equilibrates to a level that increases monotonically with extracellular concentration, maintaining very low extracellular concentrations for a long time cannot give a high peak intracellular level. This is the reason why very long durations of continuous infusion are also less effective. The balance between these effects leads to an optimal length of time for continuous infusion, as seen in Figures 1 and 2. With liposomal delivery, the rates of release of drug from the liposomes are either very slow (in the absence of heat) or very fast (upon hyperthermia). Therefore, liposomal delivery may be difficult to optimize.

The results of Figures 1–6 are dependent on the cellular pharmacokinetic parameters, which may vary among tumors. It is well established, however, that transport across the cell membrane is saturable, and that cellular transmembrane transport of doxorubicin takes hours and is slower than the other transport steps (Table 2). These conditions imply that peak intracellular concentration is maximized at an optimal continuous infusion duration. The values of this optimal duration may differ from Figure 2b for other tumor types.

The most important prediction of the model is the dependence of drug delivery of doxorubicin to a tumor on the schedule of administration. Doroshow [7] concluded that “essentially equivalent antitumor activity is observed whether the anthracycline is given as a single large bolus dose once a month, as a weekly intravenous bolus, or as a prolonged infusion.” This conclusion is based on the clinical studies cited earlier [4] showing nearly equivalent antitumor responses from bolus injection and continuous infusion. Legha et al. [4] used infusion durations of 24 to 96 hours. Figure 2a shows that peak intracellular concentrations for such long infusion times are very low, and this may explain why higher response was not seen with these particular schedules of continuous infusion. The present model suggests a need for clinical trials with shorter infusion times.

The model presented here for liposomal delivery provides some insight into the effect of liposome pharmacokinetics. The half-life used here (Table 1) is for liposomes coated with polyethylene glycol. Murine studies suggested that their long circulation half-life relative to uncoated liposomes resulted in greater drug accumulation in tumors [53]. However, Parr et al. [54] compared PEG-coated with noncoated liposomes and concluded that PEG-coating may have little advantage. The model here shows that the liposome half-life should not be much shorter than the timescale for release of contents, because if it were, most of the drug would be cleared before it was released. Figure 3 shows that the optimal value of time constant for drug release is less than 3 hours. From Allen [10], the initial and terminal half-lives of PEG-coated liposomes containing doxorubicin (at 25 mg/m² dose) are 3.2 and 45.2 hours, whereas for uncoated liposomes at the same dose they are 0.29 and 6.7 hours. Thus, at least the terminal half-life of these uncoated liposomes is not too short relative to the optimal time constant of release. With optimal, rather than very slow, rates of drug release, it is therefore unclear whether PEG-coating provides a significant advantage.

The rationale for the development of thermoliposomes has involved several factors, one of which is the increased uptake of doxorubicin by cells on heating. The model predictions here suggest that this effect is insignificant because extracellular to intracellular transport under In vivo conditions appears to be limited by saturation rather than by the rate of uptake at very low intracellular concentrations. In contrast, the increase in vessel hydraulic conductivity on heating is predicted to result in significant increased intracellular levels. There are conflicting reports on whether heat actually increases cell kill at the same intracellular doxorubicin levels. Nagaoka et al. [21] report an increase, whereas Rice and Hahn [63] found, for doxorubicin administered simultaneously with heating, that “the mechanism of increased cytotoxicity observed with simultaneous exposure is simply one of increased drug permeability.” Urano et al. [61] found synergism only for heating times longer than 60 minutes. This issue was not addressed in this paper, and is further complicated by the fact that any genuine synergism between heat and toxicity will also result in increased toxicity to normal cells. This study may therefore underestimate both tumor cell kill and host toxicity.

In conclusion, this study suggests that outcome from continuous infusion of doxorubicin could be improved by using optimal durations of infusion. The optimal duration depends on the cellular pharmacokinetics of the particular tumor cells, and for the tumor considered here is in the range 1 to 3 hours. The optimal duration increases with increasing dose. Continuous infusion, when the optimal infusion duration is used, is predicted to be superior to bolus injection and liposomal delivery. The rate of drug release from nonthermosensitive liposomes is found to be an important parameter. If this rate is optimized, nonthermosensitive liposomes are slightly less efficient than continuous infusion, but do not appear to offer any advantage in reduced toxicity. However, quite different conclusions might be reached for other drugs for which equilibration across the cell membrane is not the rate-limiting transport step. Thus, the fact that clinical trials have not yet shown benefit from using liposomal formulations of doxorubicin except in the case of Kaposi's sarcoma should not necessarily discourage the investigation of other drugs encapsulated in liposomes. Thermosensitive liposomes combined with hyperthermia have a potential advantage over continuous infusion for some doses, but only if the blood is not heated significantly while passing through the area where hyperthermia is applied.