Monte Carlo Validation of the Dorfman-Berbaum-Metz Method Using Normalized Pseudovalues and Less Data-Based Model Simplification

Abstract

Rationale and Objectives

Two problems of the Dorfman-Berbaum-Metz (DBM) method for analyzing multireader ROC studies are that it tends to be conservative and can produce AUC estimates outside the parameter space – i.e., greater than one or less than zero. Recently it has been shown that the problem of AUC (or other accuracy) estimates outside the parameter space can be eliminated by using normalized pseudovalues, and it has been suggested that less data-based model simplification be used. Our purpose is to empirically investigate if these two modifications – normalized pseudovalues and less data-based model simplification – result in improved performance.

Materials and Methods

We examine the performance of the DBM procedure using the two proposed modifications for discrete and continuous ratings in a null simulation study comparing modalities with respect to the ROC area. The simulation study includes 144 different combinations of reader and case sample sizes, normal/abnormal case sample ratios, and variance components. The ROC area is estimated using parametric and nonparametric estimation.

Results

The DBM procedure with both modifications performs better than either the original DBM procedure or the DBM procedure with only one of the modifications. For parametric estimation with discrete rating data, use of both modifications resulted in the mean type I error (0.043) closest to the nominal .05 level and the smallest range (0.050) and standard deviation (0.0108) across the 144 type I error rates.

Conclusions

We recommend that normalized pseudovalues and less data-based model simplification be used with the DBM procedure.

Introduction

There are several different statistical methods for analyzing multireader ROC studies, with the Dorfman-Berbaum-Metz (DBM) method [1–3] being the most frequently used. The DBM method involves an analysis of variance (ANOVA) of pseudovalues computed with the Quenouille-Tukey jackknife [4–6]. The basic data for the analysis are pseudovalues corresponding to modality-reader ROC accuracy measures, such as the area under the ROC curve (AUC), computed by jackknifing cases separately for each reader-modality combination. A mixed-effects ANOVA is performed on the pseudovalues to test the null hypothesis that the average accuracy of readers is the same for all of the diagnostic tests studied. Accuracy can be characterized using any accuracy measure, such as sensitivity, specificity, area under the ROC curve, partial area under the ROC curve, sensitivity at a fixed specificity, or specificity at a fixed sensitivity. Furthermore, these measures of accuracy can be estimated parametrically or nonparametrically; the DBM method accuracy estimates are the corresponding jackknife estimates. Software for implementing the DBM method is available to the public [7].

One problem with the DBM procedure is that jackknife accuracy estimates can be outside the parameter space; in particular, jackknife AUC estimates can sometimes be greater than 1 or even less than 0. For example, if the binormal maximum likelihood estimate (MLE) for the AUC is .97 and the jackknife AUC estimate is 1.02, clearly most investigators would prefer to report the MLE. For trapezoidal-rule (trapezoid) AUC estimates this is not a problem, since the trapezoid and corresponding jackknife AUC estimates are equal [8].

Another problem is that the DBM procedure tends to be conservative. Roe and Metz [2] evaluated the performance of the DBM method for continuous rating data in a Monte Carlo study, while Dorfman et al [3], using the same simulation framework as Roe and Metz, evaluated the performance for discrete rating data. In both studies the empirical type I error rates for the DBM method are usually either in close agreement with the nominal significance levels or conservative. Dorfman et al [3] conclude that the DBM method provides a “moderately conservative statistical test of modality differences”, with the degree of conservatism greatest with very large ROC areas and decreasing as the number of cases increases. The downside of a conservative test is that the power is diminished as compared to the same test with the critical value adjusted to yield significance levels closer to the nominal level.

Recently Hillis et al [8] generalize the DBM method by showing how it can be used with normalized pseudovalues, which allow the procedure to be based on the original accuracy estimates rather than the jackknife accuracy estimates. Although use of the normalized pseudovalues eliminates the problem of jackknife accuracy estimates outside the parameter space, they do not empirically investigate the performance of the DBM procedure using normalized pseudovalues. They also give conceptual reasons for using less data-based model simplification than used by Dorfman et al [3], but again do not empirically evaluate this approach.

Our purpose is to empirically investigate the performance of these two suggested modifications – normalized pseudovalues and less data-based model simplification. We conduct simulations using the same simulation structure used by Dorfman et al [3] and compare the modified procedure with the originally proposed procedure. We find that both modifications result in improved performance. Finally, we illustrate the proposed modifications with two examples.

Materials and Methods

The DBM Model and Method

The DBM method is typically used with the modality × reader × case study design where each case (i.e., patient) undergoes each of several diagnostic tests and the resulting images are evaluated once by each reader. Throughout we assume that the data have been collected using this factorial design. The competing modalities can be compared using the DBM method; in particular, the null hypothesis of no modality effect can be tested and confidence intervals for modality differences can be computed. Results generalize to both the population of cases and the population of readers; specifically, we can test if the expected value of the accuracy measure for a randomly selected reader interpreting randomly selected cases is the same for each treatment. To simplify the narration we assume that the outcome is the area under the ROC curve, although more generally any accuracy measure can be used.

For the DBM method AUC pseudovalues are computed using the Quenouille-Tukey jackknife separately for each reader-modality combination as described in Dorfman et al [1]. Let Y_ijk denote the AUC pseudovalue for modality i, reader j, and case k; by definition $Y_{ijk}=c{\widehat{\theta }}_{ij}–(c–1){\widehat{\theta }}_{ij(k)}$, where c denotes the number of casees, ${\widehat{\theta }}_{ij}$ denotes the AUC estimate based on all of the data for the ith modality and jth reader, and ${\widehat{\theta }}_{ij(k)}$ denotes the AUC estimate based on the same data but with data for the kth case removed. Using the Y_ijk as the responses, the DBM procedure tests for a modality effect using a fully crossed three-factor ANOVA with modality treated as a fixed factor and reader and case as random factors. The jackknife estimate of the AUC for the ith modality and kth reader is given by $Y_{ij\cdot }=\frac{1}{c}\sum _{k=1}^c{Y}_{ijk}$, the mean of the corresponding pseudovalues. We refer to the Y_ijk as the raw pseudovalues.

The analysis model is given by

$$Y_{ijk}=\mu +{\tau }_i+R_j+C_k+{(\tau R)}_{ij}+{(\tau C)}_{ik}+{(RC)}_{jk}+{(\tau RC)}_{ijk}+{\varepsilon }_{ijk},$$ (1)

i = 1,. . . ,t, j = 1,. . . ,r, k = 1,. . .,c,where τ_i denotes the fixed effect of modality (or treatment) i, R_j denotes the random effect of reader j, C_k denotes the random effect of case k, the multiple symbols in parentheses denote interactions, and ɛ_ijk is the error term. Main fixed effects are denoted with a Greek letter and random effects with a capital English letter. The interaction terms are all random effects. The random effects are assumed to be mutually independent and normally distributed with zero means and variances σ²_R, σ²_C, σ²_τR, σ²_τC, σ²_RC, σ²_τRC, and σ²_ɛ, where the subscript indicates the corresponding random effect. Since there are no replications, σ_τRC and σ²_ɛ are inseparable and hence we define σ² = σ²_τRC + σ²_ɛ

The DBM F statistic for testing for a treatment effect is the conventional mixed-model ANOVA F statistic based on the pseudovalues. Letting MS(T), MS(T*R), MS(T*C), and MS(T*R*C) denote the means squares corresponding to the treatment, treatment × reader, treatment × case, and treatment × reader × case effects, respectively, the F statistic for testing for a treatment effect for model (1) is given by

$$F=\frac{\text{MS(T)}}{\text{MS(T}*\text{R)}+\text{MS(T}*\text{C)}–\text{MS(T}*\text{R}*\text{C)}}$$ (2)

We conclude that there is a significant modality effect if the F ratio exceeds the (1 − α) 100th percentile of an F_df1,df2 distribution, where α is the significance level, df₁ = t − 1, and df₂ is the Satterthwaite [9, 10] degrees of freedom approximation given by

$$\frac{{[\text{MS(T}*\text{R)}+\text{MS(T}*\text{C)}–\text{MS(T}*\text{R}*\text{C)}]}^{\text{2}}}{\frac{{\text{MS(T}*\text{R)}}^{\text{2}}}{(t–1)(r–1)}+\frac{{\text{MS(T}*\text{C)}}^{\text{2}}}{(t–1)(c–1)}+\frac{{\text{MS(T}*\text{R}*\text{C)}}^{\text{2}}}{(t–1)(r–1)(c–1)}}.$$ (3)

Data-Based Model Simplification

It is possible for the F statistic (2) to be negative due to a negative denominator; in this situation the F distribution approximation is not adequate since a negative outcome is impossible for a random variable with an F distribution. Although several courses of action exist when a negative denominator occurs, few of them are satisfactory [11]. Often the action taken is to simplify the model by omitting variance components from the model that have zero or negative estimates and then to re-estimate the model.

Taking this approach, Dorfman et al [1, 3] suggest that model (1) be simplified by omitting (or equivalently, setting to zero) the treatment × reader and the treatment × case variance components if the corresponding estimates are not positive. For the simplified model the appropriate F statistic contains only one mean square in the denominator and hence cannot be negative. Specifically, they use the following rules to determine the denominator of the F statistic:

1. If MS(T*R)/MS(T*R*C) ≤ 1 and MS(T*C)/MS(T*R*C) ≤ 1 , assume σ²_τR = σ²_τC = 0 and use MS(T*R*C).

2. If MS(T*R)/MS(T*R*C) ≤ 1 and MS(T*C)/MS(T*R*C) > 1 , assume σ²_τR = 0 and use MS(T*C).

3. If MS(T*R)/MS(T*R*C) > 1 and MS(T*C)/MS(T*R*C) ≤ 1 , assume σ²_τC = 0 and use MS(T*R).

4. If none of the conditions for rules (a) – (c) hold, then no model simplification is recommended and the F statistic (2) is used.

The F statistic denominator degrees of freedom df₂ for (a), (b), (c), and (d) is (t − 1) (r −1) (c − 1), (t − 1) (c − 1), (t − 1) (r − 1), and df₂ as defined by equation (3), respectively. We refer to the use of rules (a – d) as original model simplification.

Hillis et al [8] and Hillis and Berbaum [12] suggest a similar approach but with less model simplification: model (1) is simplified by omitting the treatment× case variance component if its estimate is not positive, but the treatment × reader variance component is never omitted. Specifically, they suggest that the denominator in equation (2) be changed according to the following rules:

(a′) If MS(T*C)/MS(T*R*C) ≤ 1, assume σ²_τC = 0 and use MS(T*R) with df₂ = t − 1) (r −1).

(b′) If the condition for (a′) does not hold, the model is not simplified and the F statistic (2) is used with df₂ defined by equation (3).

We refer to the use of rules (a′) and (b′) as new model simplification. The original and new model simplification rules are compared in Table 1.

Table 1.

Comparison of Original and New Model Simplification.

	original model simplification		new model simplification
condition	assumptions	MSden	assumptions	MSden
(a) MSTR/MSTRC ≤ 1 and MSTC/MSTRC ≤ 1	σ2τR = σ2τC = 0	MSTRC	σ2τC = 0	MSTR
(b) MSTR/MSTRC ≤ 1 and MSTC/MSTRC > 1	σ2τR = 0	MSTC		MSTR + MSTC − MSTRC
(c) MSTR/MSTRC > 1 and MSTC/MSTRC ≤ 1	σ2τC = 0	MSTR	σ2τC = 0	MSTR
(d) MSTR/MSTRC > 1 and MSTC/MSTRC > 1		MSTR + MSTC − MSTRC		MSTR + MSTC − MSTRC

MS_den: F statistic denominator mean square for testing H₀: equal treatment effects.

The original and new model simplification F statistics are easily compared by writing F in the form

$$F=\frac{\text{MS(T)}}{x_1+x_2+x_3}$$ (4)

where x₁ = MS(T*R) − MS(T*R*C), x₂ = MS(T*C) MS(T*R*C), and x₃ = MS(T*R*C). Original model simplification implies setting x₁ and x₂ to zero in equation (4) if they are negative, while new model simplification implies setting only x₂ to zero if it is negative. It follows that if x₁ is not negative, that is, if MS(T*R) ≥ MS(T*R*C), then F_new = F_orig, where F_new and F_orig denote the F statistics corresponding to new and original model simplification, respectively; in this case, the denominator degrees of freedom is the same for F_new and F_orig. In contrast, if MS(T*R) < MS(T*R*C) then F_new > F_orig and the denominator degrees of freedom differs.

Conceptual reasons given by Hillis and Dorfman [12] for using less data-based model simplification as described by rules (a′) and (b′) are the following. (1) The assumption that σ²_τR = 0 in rules (a) and (b) is unrealistic since it implies that differences between treatments are the same for all readers in the population; furthermore, this assumption cannot be supported by the data for typical studies with only a few readers since the estimate of σ²_τR lacks precision. (2) The assumption σ²_τC = 0 in rules (a), (c), and ( a′) implies that the AUC estimate covariances between different readers using the same modality are the same as between different readers using different modalities; this is an acceptable assumption that can be supported by the data for typical studies having a moderate or large number of cases. (3) The motivation for rules (a – d) is to avoid a zero or negative denominator in equation (2), but this can be accomplished by simplifying model (1) only if the estimate for σ²_τC is not positive, which is the approach given by rules ( a′) and ( b′).

Normalized Pseudovalues

Hillis et al [8] generalize the DBM method by showing how it can be used with normalized pseudovalues Y_ijk^* , defined by $Y_{ijk}^{*}=Y_{ijk}+({\widehat{\theta }}_{ij}–Y_{ij\cdot })$. That is, the normalized pseudovalue for patient k, reader j, and treatment i is equal to the sum of the raw pseudovalue Y_ijk and the difference between the ijth treatment-reader original and jackknife AUC estimates. They show that the F statistic (2) based on the normalized pseudovalues is a valid test statistic and that the estimate for θ_ij, given by $Y_{ij\cdot }^{*}=\frac{1}{c}\sum _{k=1}^c{Y}_{ijk}^{*}$, is equal to the original AUC estimate ${\widehat{\theta }}_{ij}$. Thus the DBM procedure with normalized pseudovalues yields single treatment and treatment-difference confidence intervals centered on the original accuracy estimates and their differences; in contrast, when raw pseudovalues are used the confidence intervals are based on jackknife accuracy estimates that can be outside the parameter space. For the special case of trapezoid AUC estimation, they show that normalized and raw pseudovalues yield identical results.

Hillis et al [8] also show that the DBM procedure and the corrected F procedure proposed by Obuchowski and Rockette [13] yield identical F statistics when based on the same procedure parameters. For instance, when normalized pseudovalues are used, the DBM procedure yields the same F statistic as the corrected F procedure using jackknife covariance estimates. Furthermore, they show that the new model simplification approach corresponds to the constraints used with the corrected F procedure. However, they do not empirically investigate the performance of the DBM procedure using either new model simplification or normalized pseudovalues.

Results

Simulation Study

In a simulation study we examine the performance of the DBM procedure using the two proposed modifications – new model simplification and normalized pseudovalues – with respect to the empirical type I error rate for testing the null hypothesis of no treatment effect. The simulation model of Roe and Metz [2] provides continuous decision-variable outcomes generated from a binormal model that treats both cases and readers as random. We use this simulation model for simulating continuous and discrete rating data. The discrete rating data, taking integer values from one to five, are created by transforming the continuous outcomes using the cutpoints used by Dorfman et al [3]: 0.25, 0.75, 1.25, and 1.75, corresponding to false-positive fractions of 0.40, 0.23, 0.11, and 0.04, respectively. The combinations of reader and case sample sizes, AUC values, and variance components are the same as used in Roe and Metz [2] and Dorfman et al [3]. Briefly, rating data are simulated for 144 combinations of three reader-sample sizes (readers = 3, 5, and 10), four case sample sizes (10+/90−, 25+/25−, 50+/50−, and 100+/100−, where “+” indicates a diseased case and “−” indicates a normal case), three AUC values (AUC = 0.702, 0.855, and 0.961), and four combinations of reader and case variance components. Two thousand samples are generated for each of the 144 combinations; within each simulation, all Monte Carlo readers read the same cases for each of two treatments. Since these are null simulations the treatment effect in the model is set to zero.

Each simulated sample is analyzed using the four possible combinations of model simplification (original or new) and pseudovalues (raw or normalized). Maximum likelihood (parametric) estimation assuming a binormal model [14, 15] and trapezoid (nonparametric) estimation is used to estimate the AUC for the discrete rating data, while for the continuous rating data only nonparametric estimation is used. For each of the 144 combinations the empirical type I error rate is the proportion of samples for which the null hypothesis is rejected. Simulations are performed using the IML procedure in SAS [16]. The parametric area-under-the-curve pseudovalues are computed using a dynamic link library (DLL), written in Fortran 90 by Don Dorfman and Kevin Schartz, that is accessed from within the IML procedure; this DLL can be obtained from the first author.

We first discuss the parametric estimation results. The parametric empirical type I error rates from the simulation study are described in Table 2. Overall, the combination of normalized pseudovalues and new model simplification combination performs the best, having the mean type I error (0.043) closest to the nominal .05 level and having the smallest range (0.050) and standard deviation (0.0108) across the 144 type I error rates.

Table 2.

Parametric Estimation Results of the Simulation Study for Discrete Rating Data.

		Type I error rates
Model simplification	Pseudovalues	N	Mean	Minimum	Maximum	Range	SD
original	raw	144	0.036	0.009	0.063	0.054	0.0124
	normalized	144	0.036	0.011	0.062	0.052	0.0111
new	raw	144	0.042	0.011	0.070	0.060	0.0123
	normalized	144	0.043	0.017	0.067	0.050	0.0108

SD: standard deviation

For parametric estimation, use of new model simplification yields a considerable improvement in performance for each pseudovalue method. The mean type I error rate for new model simplification is much closer to the nominal .05 rate than for original model simplification: new = 0.043 vs. original = 0.036 for normalized pseudovalues, and new = 0.042 vs. original = 0.036 for raw pseudovalues. In addition, for each pseudovalue method the standard deviation of the type I error rates for new model simplification is slightly smaller than for original model simplification. Since the F statistics and denominator degrees of freedom are the same for original and new model simplification if MS(T*R) ≥ MS(T*R*C), the increase in the type I error rates using new model simplification is due to rejecting H₀ more often for those samples where MS(T*R) < MS(T*R*C).

In contrast, use of normalized pseudovalues yields only a small improvement in performance for each model simplification method. The mean type I error rates for raw and normalized pseudovalues differ only slightly: raw = .036 vs. normalized = .036 for original model simplification; and raw = 0.042 vs. normalized = 0.043 for new model simplification. However, the normalized pseudovalue type I error rates have a slightly smaller range and standard deviation than the raw pseudovalue type I error rates for each model simplification method.

The parametric empirical type I error rates are displayed in dot plots in Figure 1. In each plot a single dot represents the type I error rate corresponding to one of the 144 simulation study design-factor combinations. Since dots representing the same type I error rate are stacked, each dot plot conveys visual information similar to a histogram while also showing the actual error rates. The dot plot for the combination of normalized pseudovalues and new model simplification shows that the type I error rates have an approximate bell-shaped distribution without extreme outliers, and compared to the other three parametric plots, have less variability with a mean closer to the nominal .05 level.

Figure 1.

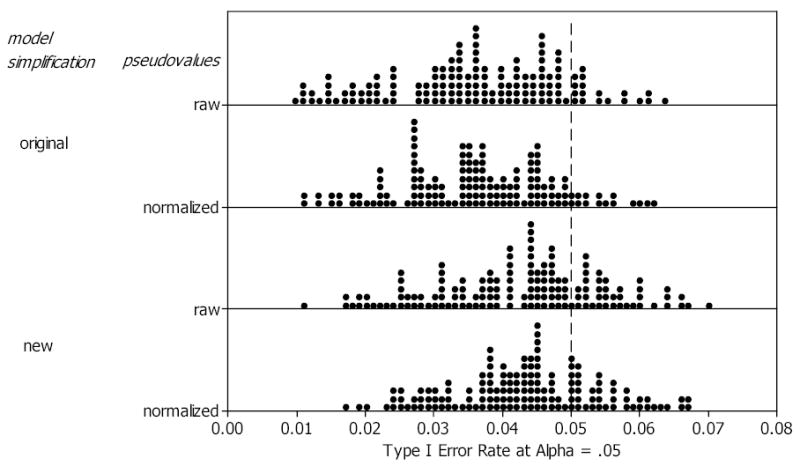
Dot plots of parametric AUC estimation empirical type I errors for the 144 combinations of reader-sample size, case-sample size, AUC, and variance components. Each dot represents one type I error rate.

Simulation results using nonparametric estimation for both discrete and continuous rating data are summarized in Table 3. Since the trapezoid estimate is the same for raw and normalized pseudovalues, we only report the original versus new model simplification results. We see that new model simplification performs better, with its mean type I error rate considerably closer to the nominal .05 rate than the original model simplification mean type I error rate: new = 0.046 vs. original = 0.041 for discrete ratings, and new = 0.043 vs. original = 0.039 for continuous ratings. Differences between new and original model simplification are small with respect to the range and standard deviation.

Table 3.

Nonparametric Estimation Results of the Simulation Study for Discrete and Continuous Rating Data.

		Type I error rates
Rating data	Model simplification	N	Mean	Minimum	Maximum	Range	SD
discrete	original	144	0.041	0.014	0.069	0.055	0.0098
	new	144	0.046	0.024	0.072	0.049	0.0100
continuous	original	144	0.039	0.008	0.070	0.062	0.0123
	new	144	0.043	0.013	0.074	0.062	0.0125

Notes: No distinction is made between raw and normalized pseudovalues since the trapezoid estimate is the same for either type of pseudovalues. SD: standard deviation

Example 1: SE versus CINE MRI for Detection of Aortic Dissection

The data for this example are provided by Carolyn Van Dyke, MD. The study [17] compared the relative performance of single Spin-Echo Magnetic Resonance Imaging (SE MRI) to CINE MRI for the detection of thoracic aortic dissection. There were 45 patients with an aortic dissection and 69 patients without a dissection imaged with both SE MRI and CINE MRI. Five radiologists independently interpreted all of the images using a 5-point ordinal scale: 1 = definitely no aortic dissection, 2 = probably no aortic dissection, 3 = unsure about aortic dissection, 4 = probably aortic dissection, and 5 = definitely aortic dissection.

Table 4 shows that the differences between the parametric and the corresponding jackknife estimates for the treatment-reader AUCs are relatively small, and hence there is little difference in the population estimates: the treatment AUC estimates based on the raw pseudovalues (i.e., the jackknife estimates) are .918 for CINE and .951 for Spin Echo, while the estimates based on the normalized pseudovalues (i.e., the parametric estimates) are .911 for CINE and .952 for Spin Echo. Table 5 presents the ANOVA table corresponding to the raw and normalized pseudovalues. Since MS(T*R) > MS(T*R*C) and MS(T*C) > MS(T*R*C) using either raw or normalized pseudovalues, there is no data-based model reduction using original or new model simplification; hence results are the same regardless of which model simplification method is used. The test statistic has the form F = MS(T)/[MS(T*R) + MS(T*C) − MS(T*R*C)] with the Satterthwaite approximation (3) used for df₂: for the raw pseudovalues F = 1.568, df₂ = 11.36, p = 0.2357, and for the normalized pseudovalues F = 2.470, df₂ = 11.53, p = 0.1912. Thus results are somewhat similar, which is not surprising since differences are attributed only to the different types of pseudovalue.

Table 4.

Parametric and Corresponding Jackknife AUC Estimates for CINE MRI and Spin-Echo MRI.

	treatment
	1 (CINE)		2 (Spin Echo)
reader (j)	${\widehat{\theta }}_{1j}$ (parametric)	Y1j· (jackknife)	${\widehat{\theta }}_{2j}$(parametric)	Y2j· (jackknife)
1	0.933	0.947	0.951	0.950
2	0.890	0.909	0.935	0.933
3	0.929	0.929	0.928	0.928
4	0.970	0.971	1.000	1.000
5	0.833	0.836	0.945	0.943
	${\widehat{\theta }}_{1\cdot }$= .911	Y1 · · = .918	${\widehat{\theta }}_{2\cdot }$= .952	Y2 · · = .951

Table 5.

ANOVA Table for Van Dyke et al [17] data.

Source	df	Raw pseudovalue mean square	Normalized pseudovalue mean Square
T	1	0.301223	0.469014
R	4	0.287974	0.297323
C	113	0.403689	0.403689
T × R	4	0.110275	0.108062
T × C	113	0.150114	0.150114
R × C	452	0.093926	0.093926
T × R × C	452	0.068255	0.068255

T: treatments; R: readers; C: cases.

Example 2: Picture Archiving Communication System versus Plain Film Interpretation of Neonatal Examinations

Franken et al [18] compared the diagnostic accuracy of interpreting clinical neonatal radiographs using a picture archiving and communication system (PACS) workstation versus plain film. The case sample consisted of 100 chest or abdominal radiographs (67 abnormal and 33 normal). The readers were four radiologists with considerable experience in interpreting neonatal examinations. The readers indicated whether each patient had normal or abnormal findings and their degree of confidence in this judgment using a five-point ordinal scale. A DBM analysis of the data using raw pseudovalues and original model reduction is presented by Dorfman et al [1].

The parametric and corresponding jackknife treatment AUC estimates are equal when rounded off to three significant digits: .868 for PACS and .850 for plain film. Table 6 presents the ANOVA table for the raw and normalized pseudovalues. Since MS(T*R) < MS(T*R*C) and MS(T*C) < MS(T*R*C) for either type of pseudovalue, then for original model simplification we assume σ²_τR = σ²_τC = 0 and use MS(T*R*C) as the denominator for F with df₂ = (t − 1) (r −1) (c − 1) = 287; in contrast, for new model simplification we only assume σ²_τC = 0 and use MS(T*R) as the denominator with df₂ = (t − 1) (r −1) = 3. LettingF_orig and F_new denote the F statistics using original and new model simplification, respectively, we have the following results: for raw pseudovalues F_orig = 0.761, df₂ = 287, p = 0.385 and F_new = 8.179, df₂ = 3, p = 0.065; for normalized pseudovalues F_orig = 0.796, df₂ = 287, p = 0.372 and F_new = 8.888, df₂ = 3, p = 0.059. Thus new model simplification method yields considerably larger F statistics and smaller p-values for each type of pseudovalue, with the p-values for the normalized pseudovalues being slightly less than for the raw pseudovalues for each model simplification method. The considerably smaller p-values for new model simplification are not surprising, since in the simulation study the higher mean type I error rate for new model simplification compared to original model simplification is due to rejecting H₀ more frequently when MS(T*R) < MS(T*R*C), as is the situation here.

Table 6.

ANOVA Table for Franken et al [18] data.

Source	df	Raw pseudovalue Mean square	Normalized pseudovalue Mean square
T	1	0.063263	0.066606
R	3	0.088753	0.097685
C	99	0.547736	0.547736
T × R	3	0.007780	0.007494
T × C	99	0.078072	0.078072
R × C	297	0.127583	0.127583
T × R × C	297	0.083643	0.083643

T: treatments; R: readers; C: cases.

Discussion

We have empirically shown that the use of normalized pseudovalues and less data-based model simplification improves the performance of the DBM procedure. For parametric estimation we found in simulations that use of both modifications resulted in empirical type I error rates that were closer to the nominal level and had less variability than those obtained using the original DBM method or using only one of the modifications. Most of the improvement was due to the use of new model simplification, with only slight improvement from use of the normalized pseudovalues. However, the normalized pseudovalues are important because the corresponding AUC (or other accuracy) estimate, computed as the mean of the normalized pseudovalues, is equal to the original AUC estimate which is within the parameter space for typical estimation methods (e.g., parametric and trapezoid). In contrast, the corresponding jackknife estimates, computed as the mean of the raw pseudovalues, can be outside of the parameter space.

Similarly, in simulations using trapezoid estimation for both discrete and continuous rating data, new model simplification resulted in empirical type I error rates closer to the nominal level, although variability was similar to that obtained from original model simplification. For trapezoid estimation no distinction was made between raw and normalized pseudovalues since the trapezoid estimate is the same for either type of pseudovalue.

Since we find that these two modifications result in improved performance and since there are conceptual reasons for not using the original model simplification method, as discussed in the Methods section, we recommend that these two modifications be used with the DBM procedure. Although the change in the type I error rate is modest, Example 2 shows that the impact can be dramatic for a particular analysis. We presently are developing stand-alone DBM software that incorporates these modifications. DBM software in the form of a SAS macro that incorporates these modifications is available from the first author.