An Improved Electronic Colon Cleansing Method for Detection of Colonic Polyps by Virtual Colonoscopy

Abstract

Electronic colon cleansing (ECC) aims to segment the colon lumen from a patient abdominal image acquired using an oral contrast agent for colonic material tagging, so that a virtual colon model can be constructed. Virtual colonoscopy (VC) provides fly-through navigation within the colon model, looking for polyps on the inner surface in a manner analogous to that of fiber optic colonoscopy. We have built an ECC pipeline for a commercial VC navigation system. In this paper, we present an improved ECC method. It is based on a partial-volume (PV) image-segmentation framework, which is derived using the well-established statistical expectation-maximization algorithm. The presented ECC method was evaluated by both visual inspection and computer-aided detection of polyps (CADpolyp) within the cleansed colon lumens obtained using 20 patient datasets. Compared to our previous ECC pipeline, which does not sufficiently consider the PV effect, the method presented in this paper demonstrates improved polyp detection by both visual judgment and CADpolyp measure.

1. Introduction

Colon cancer is the third most common human malignancy and the second leading cause of cancer-related deaths in the United States in 2004 [1]. It results in more than 130,000 new cases and 56,000 deaths each year. The overall risk of developing the disease is approximately 5% over a lifetime. More than 90% of colon cancers develop from adenomatous polyps, which take five to 15 years for malignant transformation. Early detection and removal of the polyps will dramatically reduce the risk of death [2].

Currently available detection methods include fecal occult blood test, sigmoidoscopy, barium enema, and fiber optic colonoscopy (OC), where OC is the gold standard for examination of the entire colon. Virtual colonoscopy (VC) is an emerging method for polyp detection throughout the entire colon. VC utilizes advanced medical imaging and computer technologies to mimic the OC navigation procedure, looking for polyps via fly-through in a virtual colon model which is constructed from patient abdominal images [3-9]. Compared to OC, VC has demonstrated the potential to become a mass screening modality in terms of safety, cost, and patient compliance [10-15]. Therefore, only suspicious findings uncovered using non-invasive VC screening would need to be re-examined by invasive OC follow-up [16, 17]. As a screening modality, VC has another advantage of utilizing computer-aided detection (CAD) techniques to examine the internal tissue image textures beyond the inner surface of the colon. A CAD scheme that automatically detects potential polyp candidates could substantially reduce the radiologists’ interpretation time (i.e., fly-through of the entire colon model may no longer be necessary) and improve their diagnostic performance with reduced false positives and false negatives [18-22]. However all current implementations of VC and CAD require a rigorous cleansing of the colon prior to the virtual examination. With some stool residues and colonic fluids remaining during patient image acquisition, the efficiency of VC and CAD will be lowered dramatically because the residues mimic polyps while the fluids may cover polyps.

Electronic colon cleansing (ECC) is a new technology that has been under development to remove the colonic materials from the acquired images [23-32]. First, the patient undergoes a less-stressful bowel preparation with oral contrast to tag the colonic materials, so that the residue stool and fluid have an enhanced image density compared with the colon/polyp tissues. Taking advantage of image segmentation and pattern recognition techniques, an ECC method can identify the enhanced colonic materials and restore a “cleansed” colon model for both VC navigation and CAD analysis. A simple approach is to apply thresholds to the images for segmentation and removal of the tagged materials. However this simple approach suffers from the partial volume (PV) effect that causes unexpected layers at the air-material interface and the tissue-material interface. In order to mitigate this PV effect, Lakare et al. [27] introduced a ray-based detection technique which utilizes a predefined profile pattern to detect the interfaces. Zalis et al. [31] presented a technique of using morphological and linear filters to mitigate the PV effect. Chen et al. [24] explored image gradient information while Liang et al. [23] explored a priori models to address the PV effect. In this paper, we propose a new ECC method for VC navigation and CAD analysis. This new method is based on PV image segmentation which quantifies the tissue mixtures in each image element or voxel rather than assuming a single tissue type in each voxel as was done in previous techniques. Following PV segmentation, a series of dilation and erosion operations are performed to remove the tagged colonic materials.

The content of this work is organized as follows. Section 2 presents the new ECC method. Validation of the method using 20 patient datasets is reported in Section 3, followed by discussion and conclusion in Section 4.

2. Methods

The ECC method presented in this section assumes that the images are obtained using a computed tomography (CT) scanner, which is the current standard for VC examination.

2.1. Partial Volume Image Segmentation Algorithm

2.1.1. Partial Volume Image Model

Let the acquired CT image density distribution Y be represented by a column vector [y₁, y₂,...,y_N]^T, where y_i is the observed density value at voxel i and N is the total number of voxels in the image. Assume the acquired image { y_i } contains K tissue types distributed inside the body. Within each voxel i, there possibly are K tissue types, where each tissue type has a contribution to the observed density value y_i at that voxel. Let tissue type k contribute x_ik to the observation y_i at voxel i, then we have $y_i={\sum }_{k=1}^K{x}_{ik}$.

Assume the unobservable variable x_ik follows a Gaussian distribution with mean μ_ik and variance ${\sigma }_{ik}^2$. If voxel i is fully filled by tissue type k, then x_ik becomes an observable variable, i.e., y_i in this case, with Gaussian probability distribution characterized by tissue parameters, μ_k and ${\sigma }_k^2$. If voxel i is partially filled by tissue type k and let m_ik be the fraction of tissue type k inside that voxel, then we have ${\mu }_{ik}\begin{array}{c}\hfill \mathit{def}\hfill \\ \hfill =\hfill \end{array}{m}_{ik}{\mu }_k$ and ${\sigma }_{ik}^2\begin{array}{c}\hfill \mathit{def}\hfill \\ \hfill =\hfill \end{array}{m}_{ik}{\sigma }_k^2$, where ${\sum }_{k=1}^K{m}_{ik}=1$, 0≤m_ik≤1 and $({\mu }_k,{\sigma }_k^2,{\mu }_{ik},{\sigma }_{ik}^2)\ge 0$. Therefore, the observed image density value at voxel i is expressed as $y_i={\sum }_{k=1}^K{m}_{ik}{\mu }_k={\epsilon }_i$ and also follows a Gaussian distribution, where ε_i is Gaussian noise associated with the observation y_i at voxel i and has zero mean and a variance of ${\sigma }_{y_i}^2={\sum }_{k=1}^K{\sigma }_{ik}^2={\sum }_{k=1}^K{m}_{ik}{\sigma }_k^2$. The probability distribution of sampling { y_i }, given the parameters { m_ik, μ_k, ${\sigma }_k^2$}, is

$$\mathrm{Pr}(Y\mid M,\mu ,\sigma )=\prod _{i=1}^N\mathrm{Pr}(y_i\mid m_i,\mu ,\sigma )=\prod _{i=1}^N\frac{1}{\sqrt{2\pi {\sum }_{k=1}^K{m}_{ik}{\sigma }_k^2}}\exp \left[-\frac{{(y_i-{\sum }_{k=1}^K{m}_{ik}{\mu }_k)}^2}{2{\sum }_{k=1}^K{m}_{ik}{\sigma }_k^2}\right]$$ (1)

where the NK×1 vector M=[m₁, m₂,...,m_N]^T with m_i=[m_i1,m_i2,...,m_iK]^T, μ = [μ₁,μ₂,...,μ_K]^T and ${\sigma }^2={[{\sigma }_1^2,{\sigma }_2^2,\dots ,{\sigma }_K^2]}^T$. The probability distribution of sampling { x_ik }, given the parameters { m_ik, μ_k, ${\sigma }_k^2$ }, is

$$\mathrm{Pr}(X\mid M,\mu ,\sigma )=\prod _{i,k=1}^{N,K}\frac{1}{\sqrt{2\pi m_{ik}{\sigma }_k^2}}\exp \left[\frac{-{(x_{ik}-m_{ik}{\mu }_k)}^2}{2m_{ik}{\sigma }_k^2}\right]$$ (2)

where the NK×1 vector X= [x₁,x₂,...,x_N]^T with x_i = [x_i1, x_i2,...,x_ik]^T. The above independent noise model represented by equations (or likelihood functions) (1) or (2) is consistent with the derived results in [33, 34]. Due to the one-to-one correspondence between the voxel density (the data: Y and X) and its label (the parameters: M, μ and σ), the independence of the conditional likelihoods (1) and (2) can be assumed. Furthermore, when signal-to-noise ratio is not small, the correlation of voxel densities can be ignored, thus, equations (1) and (2) approximately hold. The local signal correlative information will be considered by an a priori model (to be described later) for an a posteriori distribution toward a maximum a posteriori probability (MAP) solution.

A similar PV image model has been described which performs down-sampling of the acquired image using discrete labels [35]. When the down sampling is performed infinite times, the previous discrete label model becomes similar to the above presented continuous model for continuous mixtures { m_ik } in the range 0 ≤ m_ik ≤ 1. Partial volume image segmentation aims to determine (a) the tissue mixtures { m_ik }, (${\sum }_{k=1}^K{m}_{ik}=1$ and 0 ≤ m_ik ≤ 1), and (b) the tissue model parameters {μ, ${\sigma }_k^2$} from the acquired image data { y_i }. This is a well-known problem of parameter estimation from incompletely observed data { y_i }, which is related to the complete unobservable data { x_ik } by $y_i={\sum }_{k=1}^K{x}_{ik}$. The well-established EM (expectation-maximization) algorithm [36, 37] is the method that we will use to estimate the parameters via conditional expectation and maximization in an iterative manner, given the measurements { y_i }.

2.1.2. Parameter Estimation by the EM Algorithm

The conditional expectation or the E-step in the EM algorithm [36], given the observed data { y_i } and the estimate { M⁽ⁿ⁾,μ⁽ⁿ⁾, σ²⁽ⁿ⁾ } in the n-th iteration, has the form of [38]

$$\begin{array}{cc}\hfill & Q(M,\mu ,\sigma \mid M^{\left(n\right)},{\mu }^{\left(n\right)},{\sigma }^{2\left(n\right)})=\mathrm{E}[\ln \mathrm{Pr}(X\mid M,\mu ,\sigma )\mid Y,M^{\left(n\right)},{\mu }^{\left(n\right)},{\sigma }^{2\left(n\right)}]\hfill \\ \hfill & =-\frac{1}{2}\sum _{i,k}\left[\ln \left(2\pi \right)+\ln \left(m_{ik}{\sigma }_k^2\right)+\frac{1}{m_{ik}{\sigma }_k^2}(x_{ik}^{2\left(n\right)}-2m_{ik}{\mu }_k{x}_{ik}^{\left(n\right)}+m_{ik}^2{\mu }_k^2)\right]\hfill \end{array}$$ (3)

where the conditional means for x_ik and $x_{ik}^2$ are given, respectively, by

$$x_{ik}^{\left(n\right)}=\mathrm{E}[x_{ik}\mid y_i,M^{\left(n\right)},{\mu }^{\left(n\right)},{\sigma }^{2\left(n\right)}]=m_{ik}^{\left(n\right)}{\mu }_k^{\left(n\right)}+\frac{m_{ik}^{\left(n\right)}{\sigma }_k^{2\left(n\right)}}{{\sum }_{j=1}^K{m}_{ij}^{\left(n\right)}{\sigma }_j^{2\left(n\right)}}\cdot (y_i-{\sum }_{j=1}^K{m}_{ij}^{\left(n\right)}{\mu }_j^{\left(n\right)})$$ (4)

$$x_{ik}^{2\left(n\right)}=\mathrm{E}[x_{ik}^2\mid y_i,M^{\left(n\right)},{\mu }^{\left(n\right)},{\sigma }^{2\left(n\right)}]={\left(x_{ik}^{\left(n\right)}\right)}^2+m_{ik}^{\left(n\right)}{\sigma }_k^{2\left(n\right)}\frac{{\sum }_{j\ne k}^K{m}_{ij}^{\left(n\right)}{\sigma }_j^{2\left(n\right)}}{{\sum }_{j=1}^K{m}_{ij}^{\left(n\right)}{\sigma }_j^{2\left(n\right)}}.$$ (5)

The maximization or the M-step in the EM algorithm determines the estimate in the (n+1)-th iteration, which maximizes the conditional expectation of equation (3). For the tissue model parameter { μ_k }, we have ${\partial Q(.)∕\partial {\mu }_k\mid }_{{\mu }_k={\mu }_k^{(n+1)}}=0$, which leads to

$${\mu }_k^{(n+1)}=\frac{{\sum }_{i=1}^N{x}_{ik}^{\left(n\right)}}{{\sum }_{i=1}^N{m}_{ik}^{\left(n\right)}}.$$ (6)

For the other tissue model parameter $\left\{{\sigma }_k^2\right\}$, we obtain

$${\sigma }_k^{2(n+1)}=\frac{1}{N}\sum _{i=1}^N\frac{x_{ik}^{2\left(n\right)}-2m_{ik}^{\left(n\right)}{\mu }_k^{\left(n\right)}{x}_{ik}^{\left(n\right)}+m_{ik}^{2\left(n\right)}{\mu }_k^{2\left(n\right)}}{m_{ik}^{\left(n\right)}}.$$ (7)

Maximizing the conditional expectation function Q(.) with respect to the tissue mixture parameter { m_ik }, under the conditions of ${\sum }_{k=1}^K{m}_{ik}=1$ and 0 ≤ m_ik ≤1, does not generally have a closed-form solution as those shown in equations (6) and (7). When only a single CT image { y_i } is available (where each voxel has only an observed density value, i.e., y_i) and under the condition of ${\sum }_{k=1}^K{m}_{ik}=1$, then if a solution exists, it is limited to have a maximum number of two tissue types in each voxel. When noise is present in the image, constraints may be needed for a regularization solution. In image processing applications, a Markov random field (MRF) a priori regularization is typically used for a MAP solution. The MRF a priori model has the following form of $\mathrm{Pr}\left(m_i\mid N_i\right)=\frac{1}{Z}\exp (-\beta {\sum }_{k=1,j\in N_i}^K{\alpha }_{ij}{(m_{ik}-m_{jk})}^2$, where N_i denotes the neighborhood of voxel i, β is a parameter controlling the degree of the penalty on the mixture M, α_ij is a scale factor reflecting the difference among different orders of the neighboring voxels, and Z is the normalization factor for the MRF model. In this study, only the first-order neighborhood system is considered and α_ij is the same for the six first-order neighbors if the image has a uniform spatial resolution in three dimensions (e.g., α_ij = 1). When the axial resolution is two times lower than the transverse resolution, then α_ij is twice as small for the two neighbors in the axial direction than for the four neighbors in the transverse plane (e.g., α_ij = 1 in transverse plane and α_ij = 0.5 in axial direction). Adding the MRF prior to equation (3), we then have a conditional a posteriori distribution about the tissue mixture { m_ik }. The conditional expectation of the posteriori distribution at the n-th iteration has a quadratic form when the variance ${\sigma }_{ik}^2=m_{ik}{\sigma }_k^2$ is fixed for the (n+1)-th iterated estimate. Then, maximizing this quadratic form $Q(.)+\mathrm{Pr}\left(m_i\mid N_i\right)$ with respect to the tissue mixture parameter { m_ik }, under the conditions of ${\sum }_{k=1}^K{m}_{ik}=1$ and 0 ≤ m_ik ≤1, has a closed-form solution. By limiting each voxel to a maximum of two tissue types, i.e., m_i2 = 1 - m_i1, we have

$$m_{i1}^{(n+1)}=\frac{x_{i1}^{\left(n\right)}{\sigma }_{i2}^{2\left(n\right)}{\mu }_1^{\left(n\right)}+{\sigma }_{i1}^{2\left(n\right)}{\mu }_2^{2\left(n\right)}-x_{i2}^{\left(n\right)}{\sigma }_{i1}^{2\left(n\right)}{\mu }_2^{\left(n\right)}+4\beta {\sigma }_{i1}^{2\left(n\right)}{\sigma }_{i2}^{2\left(n\right)}\sum _{j\in N_i}{\alpha }_{ij}{m}_{j1}^{\left(n\right)}}{{\mu }_1^{2\left(n\right)}{\sigma }_{i2}^{2\left(n\right)}+{\mu }_2^{2\left(n\right)}{\sigma }_{i1}^{2\left(n\right)}+4\beta {\sigma }_{i1}^{2\left(n\right)}{\sigma }_{i2}^{2\left(n\right)}\sum _{j\in N_i}{\alpha }_{ij}}.$$ (8)

Equations (6), (7) and (8) provide a MAP-EM solution for PV image segmentation under the constraint that each voxel has a maximum of two tissue types. However, there is no limitation on the number of tissue types in the image. In our case, the CT image may contain four tissue types with different image densities, i.e., K = 4: (i) air in the colon lumen and lungs, (ii) fat or soft tissues, (iii) muscle, and (iv) bone or tagged colonic materials. Such information can be utilized to facilitate the segmentation of a CT image into mixtures with a maximum of two tissue types in each voxel. Given a global concave posteriori distribution, the EM algorithm has been proven to climb up the hill or converge to the maximum point [36, 39]. In our study, the quadratic form is concave, but not necessarily global concave, therefore, the MAP-EM solution could be a local maximum.

2.1.3. Use of Available Tissue Types to Improve the PV Image Segmentation

MRF prior model is generally applicable to any number of tissue types in each voxel. However, given a single CT image, a solution exists for a maximum of two tissue types in each voxel. When there are four tissue types present in the CT image, we have a total of 15 possible tissue mixtures as shown in Table 1. In practice, there is a very small probability that all four tissue types will be in a voxel. Most voxels are dominated by a single tissue type. The next most common scenario is when voxels contain two tissue types because they are situated on the boundary. Some voxels may contain three tissue types when they are on the intersection of two borders of three tissue types, e.g., the border of the air and the tagged colonic material intersects the colon wall. In this case, only the two dominating tissue types will be considered. A general rule to constrain the possible tissue mixtures shown in Table 1 into two tissue mixtures is outlined below.

Table 1.

A total of 15 possible tissue mixtures for four tissue types in a CT image.

Index	Tissue types	Index	Tissue type
1	Air only	9	Tissue and bone
2	Tissue only	10	Muscle and bone
3	Muscle only	11	Air, tissue and muscle
4	Bone only	12	Air, tissue and bone
5	Air and tissue	13	Air, muscle and bone
6	Air and muscle	14	Tissue, muscle and bone
7	Air and bone	15	Air, tissue, muscle and bone
8	Tissue and muscle

By considering three-dimensional (3D) spatial information around a voxel, the maximum number of two tissue types can be enforced by selecting the most likely solution. In this study, we use an iterative algorithm for PV image segmentation. After each iteration, the PV segmentation result can easily be transferred into a hard segmentation by labeling each voxel with the dominant tissue type in that voxel. This hard segmentation result reflects the neighborhood voxels’ tissue types. The mixture in the current voxel is comprised of the two most dominant tissue types in the neighboring voxels. For example, if the first-order neighborhood system is considered, we have a total of 6 neighbors. These six voxels are labeled as either air, tissue, muscle, or bone/tagged materials (TM). If three voxels are labeled as bone/TM and two are labeled as air, the current voxel is highly likely to contain a mixture of air and bone/TM. If the six voxels are labeled equally as air, tissue, and bone/TM, then the air components in the corresponding voxels will be added. We repeat this process for the tissue and bone/TM components. The two types with larger summations will be assumed as the mixture in the current voxel.

2.1.4. Implementation of the PV Image Segmentation Algorithm

Implementation of the presented iterative PV image segmentation algorithm starts with an initialization step. A simple threshold is used for hard segmentation. From this hard segmentation, the initial four tissue-type (i.e., the air, soft tissue, muscle, and bone/TM) or model parameter sets $\{{\mu }_k^{\left(0\right)},{\sigma }_k^{2\left(0\right)}\}$ are estimated using the labeled voxel density values. The initial tissue mixture $\left\{m_{ik}^{\left(0\right)}\right\}$ is determined from the hard segmentation result by assuming each voxel is 100% occupied by a single tissue type. As the iteration proceeds, convergence is assumed when the following termination criterion is satisfied: $\mathit{Max}\left({\mid \frac{{\mu }_k^{(n+1)}}{{\mu }_k^{\left(n\right)}}-1\mid }_{k=1,2}\right)<\gamma$ . When the maximum difference between the means of each tissue class at the n-th and the (n+1)-th iterations is less than the specified threshold γ, the iteration process is terminated. In this work, γ is set to be 0.05. Our experiments show that four iterations are usually sufficient to satisfy the criterion and converge to good segmentation results. The penalty parameter β was chosen in the range of [0.1, 1.0] and good noise control was observed.

2.2. Cleansing Colon Lumen from the PV Segmentation

After the iterative PV image segmentation is terminated, the voxels in the colon lumen are classified as air, mixture of air with tissue, mixture of air with tagged materials, or mixture of tissue with tagged materials. Cleansing the colonic materials is performed by a series of dilation and erosion operations [40] as well as region growing strategies.

In general, there exist two major challenges for electronic colon cleansing (ECC). The first is the removal of the interface layer between the air and the tagged colonic materials in Figure 1(d). Due to the PV effect and other errors (from scanner, patient motion, and image reconstruction procedure, especially the interpolation), the CT image density at the interface layer varies from the low end of -900HU (air) to the high end of 400HU (enhanced residues), see Figure 1(c). This layer covers the density values of colon tissues and so it is impossible to distinguish the voxels of colonic materials in this layer from that of the colon tissues. A simple threshold approach generates this interface layer in Figure 1(b). Another challenge is the restoration of the CT density values of colon tissues in the enhanced mucosa layer in Figure 1(c) and (d). A good ECC method should identify the enhanced mucosa layer and remove the portion with tagged colonic materials. Partial volume image segmentation is a desirable (theoretically-based) approach to identify the layers, quantify the material/tissue mixtures in the layers and restore the true CT density values of the colon mucosa layer. In the following, the voxels which are related to the layers will implicitly indicate the potential PV voxels, while others outside the layers are almost assured to be non-PV voxels, in order to take the errors of non-PV effect into the presentation.

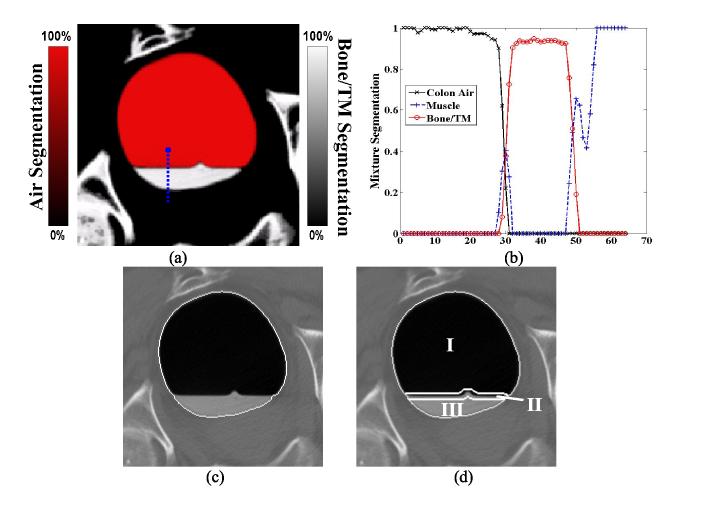
Figure 1.

A CT image slice of the colon with enhanced colonic materials (a). The white vertical line indicates a sample path for the profile of picture (c). A threshold of 200HU (Hounsfield unit) generates a segmentation of picture (b). Picture (d) shows the corresponding density profile from (b) along the vertical line in (a). The interface layer is a mixture of air and tagged colonic materials. The enhanced mucosa layer is a mixture of colon tissues and tagged materials.

2.2.1. Identifying the Interface Layer

Normally, PV image segmentation provides correct tissue/material mixtures within the interface and mucosa layers. A region growing on the PV segmentation is sufficient to cleanse the colonic materials. However in some cases, it may identify an incorrect mixture component in these layers. Figure 2(b) shows an example of such incorrectly segmented mixtures in voxels around location 30 along the vertical profile. In order to avoid such cases when identifying the interface layer, we utilize the well-known dilation-erosion strategy [40]. Let the colon air segmentation volume be S^a, which consists of the air component { m_air } in the voxel array. Similarly, we define the tagged colonic material segmentation volume as S^t. For each volume, we apply a 3D dilation operation by a three-cubic strel matrix

$$D^a=\mathit{Dilation}(S^a,\mathit{strel}),D^t=\mathit{Dilation}(S^t,\mathit{strel}),\mathit{strel}={\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right]}^T\cdot \left[\begin{array}{ccc}\hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right].$$ (9)

Then we construct a new volume S^e by applying the erosion operation on the sum of D^a and D^t, i.e., S^e = Erosion((D^a + D^t), strel).

Figure 2.

Picture (a) shows the mixture-based PV segmentation result from the corresponding image slice of Figure 1(a). In this picture, the red color (or air space) indicates the segmentation result for the colon air class; the white color (or tagged material space) indicates the segmentation result for the bone/tagged material (TM) class. Between these two colors/spaces is the interface layer. Picture (b) shows the corresponding segmentation profiles along the sample vertical line (or blue color) which is the same as shown in Figure 1(a). In most cases, the PV segmentation provides correct material mixtures in the layers, but in some cases, it may identify an incorrect mixture component. Picture (b) shows an example, where some voxels around location 30 along the vertical profile in the interface layer contain colon tissue component. This error must be corrected. Picture (c) illustrates the border of volume S^e (i.e., the entire lumen enclosure). Picture (d) shows the divided regions in the enclosure volume. Region I is the air space P^a, region II is marked as the interface layer space P^m, and region III is the tagged material space P^t .

The new volume S^e covers the entire colonic (lumen plus mucosa) space including the tagged material region and the interface layer, as shown in Figure 2(c). Based on the three volumes D^a, D^t and S^e, we divide the entire colonic space into three parts according to the following criteria

$$\begin{array}{cc}\hfill P^m& =\{{\mathit{voxel}}_i\mid S_i^e>0,D_i^a>0,D_i^t>0\}\hfill \\ \hfill P^a& =\{{\mathit{voxel}}_i\mid {\mathit{voxel}}_i\notin P^m,S_i^e>0,D_i^a>0,D_i^t=0\}\hfill \\ \hfill P^t& =\{{\mathit{voxel}}_i\mid {\mathit{voxel}}_i\notin P^m,S_i^e>0,D_i^a=0,D_i^t>0\}\hfill \end{array}$$ (10)

where P^a represents the colonic air space or region I in Figure 2(d), P^t reflects the tagged material region III in the figure, and P^m indicates the interface layer area II.

2.2.2. Cleansing the Colon Lumen and Restoring the CT Density Values of the Colon Tissues in the Enhanced Mucosa Layer

The colon lumen consists of the entire region I, the majority of region II and a small contribution from region III in Figure 2. Therefore, all voxels in region I or space P^a are classified as colon lumen voxels. For each voxel i in spaces P^t and P^m, their CT image density values $I_i^{\mathit{new}}$ are altered by

$$I_i^{\mathit{new}}=\{\begin{array}{cc}{I}_i^{\mathit{original}}+({\mu }_1-{\mu }_4)\cdot m_{i4}+({\overline{I}}_i-I_i^{\mathit{original}})\cdot m_{i4}\hfill & \hfill \mathit{if}{\overline{I}}_i\ge I_i^{\mathit{original}}\\ I_i^{\mathit{original}}+({\mu }_1-{\mu }_4)\cdot \left(m_{i4}+\frac{(I_i^{\mathit{original}}-{\overline{I}}_i)\cdot m_{i4}}{{\mu }_4}\right)\hfill & \hfill \mathit{if}{\overline{I}}_i<I_i^{\mathit{original}}\end{array}\phantom{\}}$$ (11)

where ${\overline{I}}_i={\sum }_{k=1}^4{m}_{ik}{\mu }_k$, and μ_k and m_ik have been defined before as the mean parameter of tissue type k in the image and the fraction of tissue type k in voxel i respectively. In equation (11), index 1 refers to the segmentation of colonic air and index 4 refers to the segmentation of the bone/TM. Using equation (11), the CT density values of all voxels in regions II and III are altered. In region III, the CT density values of those voxels containing mixtures of colon tissues and tagged materials (TM) are restored, and other voxels are converted to air or classified as colon lumen voxels by equation (11). The remaining task in our new ECC method is to restore and classify the voxels in region II.

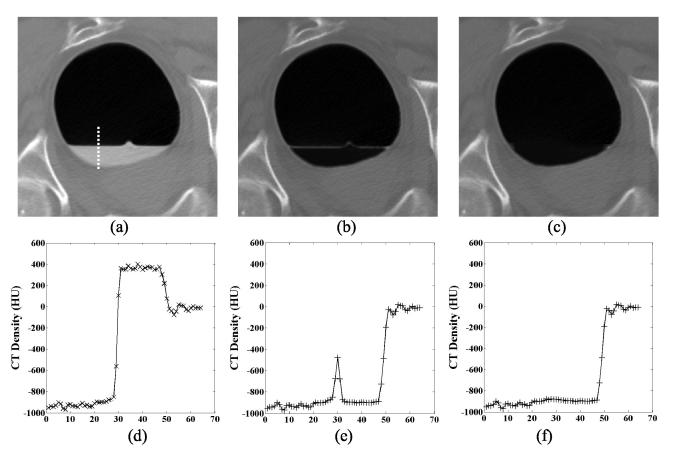
In region II, the voxels on each side (or at each boundary) of the interface layer are altered by equation (11), but not completely restored due to the presence of more than two tissue types. Some small spots may be retained along the horizontal direction in region II after processing by equation (11) and is shown in Figure 3(b). We have conducted experiments to demonstrate that the PV effect at the interface layer has been transformed to a patch-like effect after equation (11), similar to Figure 3(b). To alleviate this effect, we introduce another equation to restore the CT density for each voxel in region II or space P^m. First, we define a subtraction volume SUB which is generated by iteration

$$\begin{array}{cc}\hfill SU{B}_i^{\left(0\right)}& =I_i^{\mathit{new}}\hfill \\ \hfill SU{B}_i^{\left(n\right)}& =SU{B}_i^{(n-1)}+\sum _{n\in \mathit{neighbor}\left(i\right)}{e}^{-{\left({\nabla }_{n}SU{B}^{(n-1)}\right)}^2}\cdot \parallel {\nabla }_{n}SU{B}^{(n-1)}\parallel \hfill \end{array}$$ (12)

where ▽ represents the first-order derivative at the given position and the neighborhood of this voxel includes that voxel itself. After three iterations of equation (12), the CT density at the interface layer is further adjusted by $I_i^{\mathit{newII}}=I_i^{\mathit{new}}-SUB$ interface layer. The CT density values in the interface layer are then reduced to a reasonable level $I_i^{\mathit{newII}}$ toward that of air level. Thus the patch-like effect is removed and the CT density restoration at both ends of region II is improved, as shown in Figure 3(c) and (f).

Figure 3.

The restored CT image density values. Picture (a) is the original CT image slice of Figure 1(a). Picture (b) shows the cleansed CT image after equation (11). In the image, all the tagged colonic materials are removed and the CT densities of the mucosa layer are restored, except for some small spots retained along the horizontal direction in the interface layer. Picture (c) shows the final cleansed CT image after equation (12). Pictures (d), (e) and (f) show the corresponding density profiles from the images along the vertical line in (a).

The converted air voxels in regions I, II and III make up the colon lumen space, from which a virtual colon model is built for VC examination. Within this space, a centerline or fly-path is determined and a potential field is constructed to facilitate the VC navigation through the entire lumen space, looking for polyps [41-46]. The geometric information of the lumen border can be analyzed by a surface-based CAD technique to detect the polyps [18-20, 47]. The restored CT density values of the mucosa layer, which is comprised of five to ten voxels beyond the lumen border, can be extracted for texture analysis for improved CAD performance [21, 22, 48]. This improved CAD is called texture-based CAD below.

3. Results

Computed tomography (CT) datasets from twenty patients were used to evaluate the efficiency of the new electronic colon cleansing (ECC) method presented in this paper and compared to our previously developed ECC pipeline in the FDA-approved commercial V3D-Colon Module (http://www.viatronix.com). These datasets were acquired from patients who followed a less-stressful bowel preparation including a low-residue diet and oral contrast tagging of the colonic materials [17]. A single-slice spiral CT scanner was used with clinically available protocols to cover the entire abdominal volume during a single breath hold. The detector collimation was 5 mm and the images were reconstructed as 1 mm thick slices of 512×512 array size. Each patient study or dataset included both supine and prone scans (resulting in a total of 40 scans). Each dataset (including both supine and prone scans) contained approximately 800 images. Nine of these twenty patient datasets contained at least one polyp larger than 5 mm in diameter. Their polyp sizes and positions were documented by optical colonoscopy (OC) reports and also verified by radiologists’ VC navigation through their colon models.

Each dataset was processed by the presented ECC method and also by our previous ECC pipeline. If the colonic materials are fully tagged, both ECC methods can cleanse the colon lumen well. The covered polyps and colon folds can be exposed for visualization and CAD analysis. In some cases, the colonic residues may not be fully tagged due to patient variation, as shown in the top row of Figure 4. The resulting CT density values are similar to that of the colon tissues. Furthermore the density variation follows an irregular pattern. Insufficient tagging is a major reason for decreased performance of our previous ECC pipeline, as seen in the middle row of Figure 4. In our previous ECC pipeline, cleansing the colon lumen is based on a hard image segmentation which assumes that each voxel contains a single tissue type and ignores the PV effect [24, 27]. In the present ECC method, cleansing the lumen is based on a PV image segmentation which quantifies the material mixtures in each voxel. An improvement is expected and can be seen in the bottom row of Figure 4.

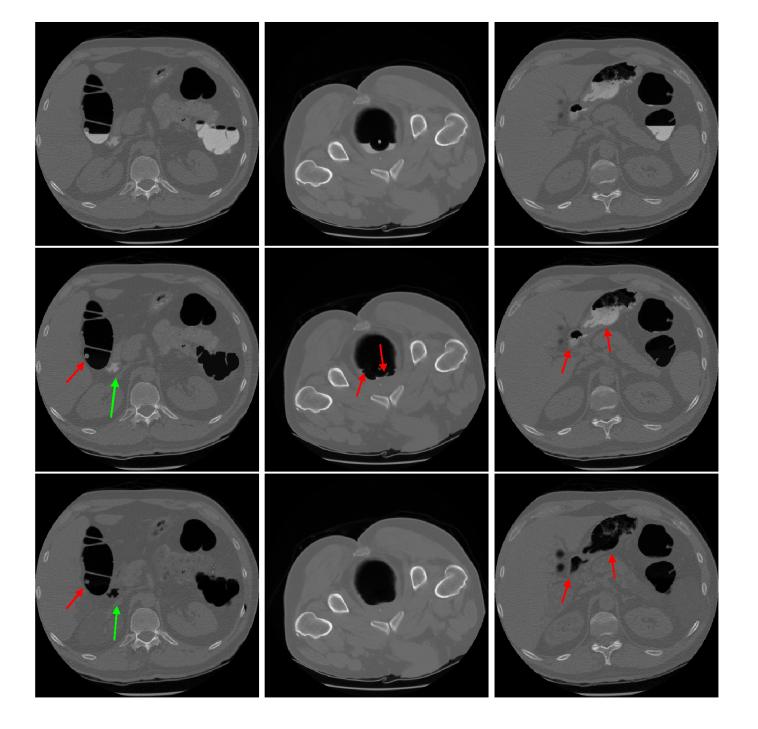
Figure 4.

Comparison of two different cleansing methods. The pictures at the top row are the original CT image slices. The results by our previous ECC pipeline are shown in the middle row. The results by this present ECC method are shown at the bottom row. The left column shows a case with a polyp covered by the colonic residues. Both methods removed the residues and uncovered the polyp successfully (see the short red arrow). However, the previous pipeline failed to cleanse a part indicated by the long blue arrow. The middle column shows an example for residues of irregular shape (but uniform tagging). The previous method left some small spots which could mimic polyps as indicated by the red arrows, while the new method did not. The right column shows an example for residues of non-uniform tagging. Due to the non-uniform density variance inside the residues as indicated by the red arrows, the previous method failed to cleanse these non-uniform tagging residues, while the new method succeeded.

In addition to the above 2D visual examination, all colon lumens were cleansed using each ECC method and input to the V3D-Colon Module for construction of virtual colon models and navigation through the colon lumens. During the fly-through navigation, the operator inspected the colon inner wall using volume-rendered 3D endoscopic views [46, 49]. Some endoscopic views are illustrated in Figure 5. The operator was asked to score the 80 virtual colon models (40 were cleansed using the present ECC method and 40 with our previous ECC pipeline) based on their endoscopic views and without knowing which ECC method was used. Both ECC methods received similar scores for nearly half of the 80 samples, however, the present ECC method was scored better on the remaining half.

Figure 5.

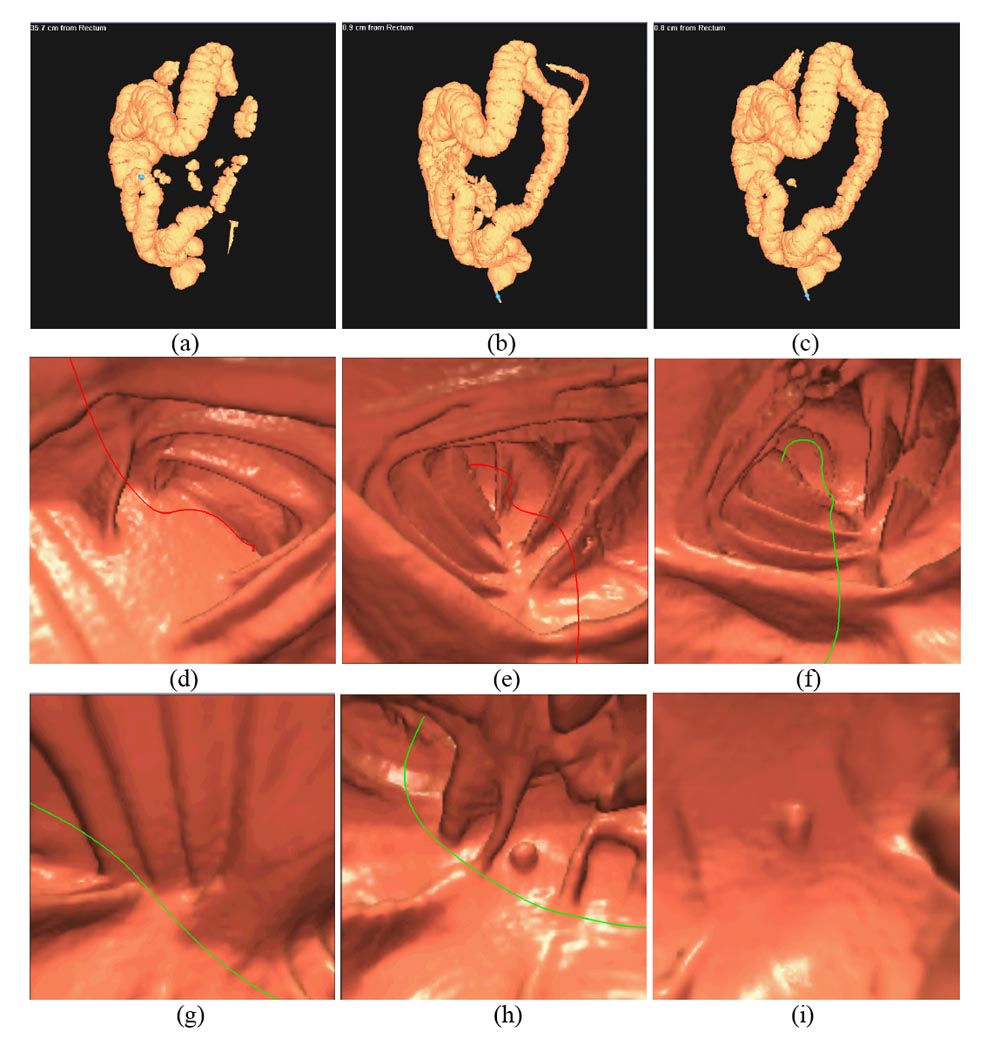
The 3D VC images or endoscopic views of the original and cleansed CT data. The left column shows the images generated from the original CT data. The middle column shows the images from the cleansed CT data by this present ECC method. The results by our precious ECC pipeline are shown on the right column. The top row shows the reconstructed 3D virtual models of the colon lumens from the original and cleansed CT data. Due to the presence of the colonic residues, the whole colon is separated into several disconnect segments. After ECC operation, the whole colon is obtained. There are some external parts retained for both ECC methods. This is a typical error from any automated image processing operation. This error can be easily corrected by the operator or by more sophisticated computer algorithm. Since it does not affect VC task of looking for polyps inside the colon, this error is ignored in this work. The middle row shows the endoscopic views before and after ECC operation. In picture (d), the navigation route is blocked by the residues. After ECC of the residues, the route resumes and more details can be seen in pictures (e) and (f). The bottom row shows a case where a polyp is covered by the residues. After ECC operation, the polyp and the colon folds under the residues are revealed. Improved performance of this presented ECC over our previous one is seen for uncover of the polyps (bottom row) and preservation of the colon folds (middle row).

In addition to the above visual judgment, we also performed computer-aided detection of polyps (CADpolyp) on the 80 cleansed colons obtained using both ECC methods. One CAD measure is the surface- or shape-based approach [47]. It combines both the traditional local principal curvature measures and a modified or smoothed version (which is called global principal curvature measures) to quantify the shape of the extracted mucosa layers from both ECC methods. Polyp detection is based on the quantitative measure of the local shape change which mimics the polyp shapes. The shape-based CADpolyp results are shown in Table 2. The present ECC method results in a noticeable improvement (less false positives) in the shape description of the extracted mucosa layers from the cleansed colons. In addition to the surface-based CAD measure, we applied our texture-based CAD to the extracted mucosa layers. This texture-based CADpolyp utilizes additional morphological and texture information of the polyp suspects detected by the shape-based approach to reduce the false positives [22, 48]. Improvement of the internal feature description of the extracted mucosa layers is also evident using the present ECC method when compared with the previous one. Given that the same CAD parameters were used for both ECC methods, the sensitivity and false-positive (FP) rate for each dataset shall reflect the varied performance of these two different ECC methods. For 100% detection sensitivity, both the surface- and texture-based CADpolyp schemes produce fewer false positives when the presented ECC method is used. This improvement is due to the improved ECC performance which handles the PV effect more accurately.

Table 2.

Comparison of CADpolyp on the virtual colons cleansed by two different ECC methods, where FP is the abbreviation of false positive as defined in the text.

	Shape-based CAD (Sensitivity∼FP Rate)	Texture-based CAD (Sensitivity∼FP Rate)
Previous ECC pipeline	100% ∼ 153.7/per dataset	100% ∼ 2.19/per dataset
Current ECC method	100% ∼ 147.7/per dataset	100% ∼ 2.06/per dataset

The presented ECC method was coded using the C++ programming language and implemented on a Pentium PC with 1.8GHz CPU speed and 1.5GB RAM memory. It took less than 20 minutes to read each DICOM volume image of approximately 400 slices, segment the image into mixtures, perform the dilation-erosion operations and write out the results for VC visualization-navigation and quantitative CADpolyp measure.

4. Discussion and Conclusion

A new ECC method was presented and evaluated with 20 patient studies. The improved performance of the new ECC method, when compared with our previous ECC pipeline, was demonstrated by visual judgment of the 2D slice show and 3D endoscopic view of the cleansed colons and also by quantitative measure using CADpolyp on the extracted mucosa layers. The improvement is mainly due to PV image segmentation which preserves more details than our previous hard segmentation does and is shown in Figure 6. Because of the lack of ground truth on the subjects, a quantitative measure on the segmented potential PV voxels from the two ECC methods is not feasible. A quantitative comparison on their segmentations by phantom experiments is desired and is under progress.

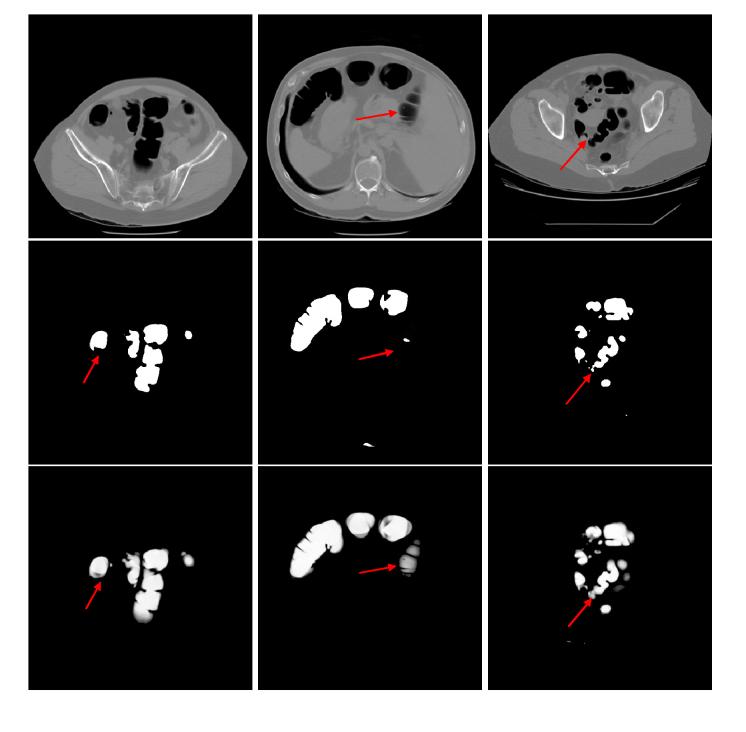
Figure 6.

Comparison of two different image segmentation methods. The pictures in the top row are the original CT image slices. The middle row shows the results of our previous hard segmentation algorithm. The results of our current PV segmentation method are shown in the bottom row. The PV image segmentation preserves more details because of its consideration of the PV effect than the hard image segmentation which does not consider the PV effect. The arrows indicate some example locations where the PV segmentation preserves more details.

The presented PV image segmentation is fully within the EM framework which maximizes the conditional expectation of the underlying tissue process given the acquired data. This differs from previous techniques [50, 51] which maximize the probability likelihood of the acquired incomplete data directly. A thorough comparison between this EM framework and the previous approaches [50, 51] is in progress.

The PV image model in this work is equivalent to the discrete PV model of [35] when the discrete down-sampling is performed infinite times and the number of labels becomes infinite. A through comparison between our continuous PV model and the discrete PV model [35] is an interesting topic and is also in progress.

The current PV presentation and that of previous work [35] share the same practice of constraining the maximum number of tissue types in each voxel to two, when even a single image can have more than two tissue types. Prior knowledge of the available tissue types may be helpful to improve the segmentation of more than two tissue types in a voxel from a single image [35, 50, 51]. In our opinion, use of multi-spectral images is a more statistically-robust approach. This multi-spectral approach to image segmentation can be based on magnetic resonance images of T₁-, T₂-, and proton density-weighted scans [38]. From these three images, we can determine with greater statistical significance the composition of a voxel with up to four tissue types. Further improvement is expected if the gravity of the tagged materials can be used as an a priori information [23], which results in a nearly horizontal surface between the air and the tagged materials.

In the derivation of the closed form of equation (8), we assumed the variance is fixed at the n-th iteration. This assumption results in a quadratic form for the posteriori cost function and makes its maximization (or minimization if the minor sign is changed to plus) numerically tractable. However, its effect on the segmentation of tissue mixture { m_ik } has not been rigorously studied, and the MAP-EM iterative convergence for { m_ik } needs to be proven mathematically. This is another interesting topic of our current research. Despite the lack of a mathematical proof, an iterative convergence for { m_ik } was observed in the experiments on all 80 data samples.

Due to many unexpected situations in the clinic, an automatic model-based approach will not provide perfect segmentation of the acquired images. Therefore, a task-specific post operation is necessary and manifested by the dilation-erosion operation employed in this paper in cleansing the colon lumen from the PV image segmentation. Other post operation shall be explored and is in progress.