Wiring optimization can relate neuronal structure and function

Abstract

We pursue the hypothesis that neuronal placement in animals minimizes wiring costs for given functional constraints, as specified by synaptic connectivity. Using a newly compiled version of the Caenorhabditis elegans wiring diagram, we solve for the optimal layout of 279 nonpharyngeal neurons. In the optimal layout, most neurons are located close to their actual positions, suggesting that wiring minimization is an important factor. Yet some neurons exhibit strong deviations from “optimal” position. We propose that biological factors relating to axonal guidance and command neuron functions contribute to these deviations. We capture these factors by proposing a modified wiring cost function.

Because brain structure is intimately related to its function, understanding structure should provide important clues to brain function. Traditionally, structural features of the brain are explained from the perspective of development, a complex process including such events as cell migration (1, 2), axonal guidance (3–5), cellular signaling (6), and synaptogenesis (7–10). Although much progress has been made in understanding the mechanisms of neural development, many unanswered questions remain. In particular, it is not known what determines the placement of neurons and synapses in the body, a question to be addressed in this paper.

Our approach for understanding neuronal structures complements neural development and relies on the existence of general principles governing the architecture of a mature brain. Specifically, we exploit the wiring economy principle proposed by Ramón y Cajal more than 100 years ago (11). This principle postulates that, for a given wiring diagram, neurons are arranged in an animal to minimize the wiring cost. The evolutionary “cost” can be attributed to factors such as wire volume (12–14) and signal delay and attenuation (15–17), as well as metabolic expenditures associated with signal propagation and maintenance (18, 19). Although the exact origin of the wiring cost is not known, the farther apart two neurons are, the more costly is the connection between them. The wiring cost can therefore be expressed as a function of distance between neurons and consequently minimized (12, 20 0–25).

Despite many successful applications of the wiring minimization principle (refs. 12–14 and 20–27, but see ref. 28), it has never been tested on the level of individual neurons for an entire nervous system. Such testing was precluded by the lack of wiring diagrams and by the computational complexity of the optimization problem. Previous works have shown that wire length minimization can explain the layout of small systems by tabulating the amount of wire required for every possible permutation of components in the network. The actual ordering of ganglia in Caenorhabditis elegans (20) and the arrangement of areas in the prefrontal cortex in the macaque (27) were found in this manner to have the shortest total wiring. Unfortunately, this brute force method is impractical for all but the smallest networks (number of components of order 10), because the number of permutations increases exponentially with the number of components. In addition, the results provide only the relative ordering of components and not their exact positions in an actual animal.

In this paper, we solve for the neuronal layout of an entire nervous system of the nematode C. elegans using the updated wiring diagram and powerful placement algorithms borrowed from computer engineering (29–33). We consider 279 neurons (pharyngeal and unconnected neurons excluded) of the hermaphrodite worm, whose identity, locations of cell bodies, sensory endings, and neuromuscular junctions, as well as the wiring diagram, have been well studied and found to be largely reproducible from animal to animal (34, 35). The length of the worm is >10 times greater than its diameter, allowing us to reduce the problem into one dimension.

By minimizing the cost of connecting the nervous system, our solution predicts the position of most neurons along the anterior–posterior (AP) body axis of the nematode worm. This result suggests that wiring minimization is a good general description of the relationship between connectivity and neuron placement. A comparison of the cost-minimized layout with actual neuron positions revealed groups of outlier neurons with distinct structural characteristics. Interestingly, neurons within each group have been shown in experiments to play similar roles in the worm nervous system: developmental pioneering and signal integration for motor control. We suggest that the results obtained from cost minimization can be used in a number of ways to infer neuron function.^§

Wiring Cost Minimization in the Dedicated-Wire Model

We start by modeling the nervous system (see Fig. 1B Inset for example) as a network of nodes that correspond to neuronal cell bodies, connected by wires that represent synapses (Fig. 1C Inset). We call such model “dedicated wire,” because each synapse has its own wire (similar to point-to-point axon design in ref. 14). Additional wires connect neurons to sensory endings and muscles. Assuming that the placement of these structures is subject to constraints independent of neuronal organization, their positions are fixed.

Fig. 1.

Actual and predicted neuronal cell body positions. (A) Neuronal layout in the worm, pharyngeal neurons excluded. Each color denotes a ganglion. (B) Actual placement of neuronal cell bodies projected onto anterior–posterior axis. Circles of the same color represent cell bodies belonging to the same ganglion. Plots for each ganglion are offset vertically to aid the eye. (Inset) Schematic example of biological network of three neurons and two fixed points: s, sensory ending; m, muscle. The blue neuron is bipolar, with one neurite attaching to the sensory ending and the other making two excitatory synapses onto the red neuron and one excitatory synapse onto the green neuron (circle represents the cell body). The red neuron makes an inhibitory synapse onto the blue neuron (line ending in circle) and a gap junction (bar) with the green neuron. The green neuron has a neuromuscular junction. (C) Neuronal layout predicted from minimization of quadratic wiring cost in dedicated-wire model. (Inset) Weighted dedicated-wire model. Each black line or wire corresponds to one synapse independent of polarity (excitatory vs. inhibitory), directionality, or modality (chemical vs. gap). (D) Neuronal layout predicted from the binary dedicated-wire model. (Inset) Binary dedicated-wire model. Each wire corresponds to a synaptic connection neglecting a multiplicity of synapses. (E) Neuronal layout predicted from the shared-wire model. (Inset) Shared-wire model. Neurons are represented as nonbranching wires (colored lines), which must overlap if a synaptic connection exists. Cell body location on the wire can be calculated by using different rules.

The total wiring cost (C^tot) can be expressed as the sum of an internal cost to connect neurons to each other (C^int) and an external cost to attach neurons to the fixed structures (C^ext):

We assume that the cost of wiring the ith and jth neurons is proportional to some power, ζ, of the distance between them. Then the total internal wiring cost is:

where x_i is the neuron position, and α is an unknown coefficient. A_ij is an element of the adjacency matrix A, representing the total number of synapses between neurons i and j in both directions. Because the wiring cost is assumed to be independent of the directionality of synapse (i.e., signal propagation from neuron i to j or vice versa), matrix A is symmetric (A_ij = A_ji). Also, the cost is assumed to be independent of synapse polarity (i.e., inhibitory vs. excitatory), so the adjacency matrix is nonnegative (A_ij ≥ 0).

The second term in Eq. 1 represents the cost of wiring neurons to sensory organs, k, located at positions s_k, and muscles, l, at positions m_l:

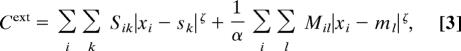where S_ik is the number of synapses between neuron i and sensory organ k, and M_il is the number of synapses between neuron i and muscle l. In the schematic network illustrated in Fig. 1C Inset, the adjacency matrix (A), neuron-to-sensory (S), and neuron-to-muscle matrices (M) are:

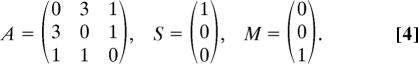To account for multiplicity of synapses on a single neurite, we apply a coefficient 1/α to neuron-to-neuron (Eq. 2) and neuron-to-muscle (second term in Eq. 3) costs based on the following. In the dedicated-wire model, the cost of connecting two neurons is directly proportional to the number of synapses between them (Fig. 1C Inset), equivalent to having a dedicated wire for each synapse. Yet, in the actual worm, the majority of neurons are nonbranching and bipolar, making an average of 58.6 en passant synapses and neuromuscular junctions with only two neurites (or two wires). This morphology can be taken into account by normalizing each neuron-to-neuron and neuron-to-muscle connection by the average number of synapses per neurite (α = 29.3 or 58.6 synapses per neuron divided between two neurites). Sensory neurons, on the other hand, typically send one specialized neurite to the sensory organ (34), which, with a few exceptions, does not make synapses with other neurons or muscles. Thus each sensory fixed point, by construction, connects to a neuron through a dedicated wire and needs not be normalized. An alternative way to incorporate this neuronal morphology is by using a “shared-wire” model (Fig. 1E Inset), which will be introduced later.

We find the optimal neuronal placement that minimizes the wiring cost function defined by Eqs. 1–3. Initially, we assume that the cost of connecting two neurons increases as the square of the distance between them (ζ = 2 in Eqs. 2 and 3). The quadratic cost function can be minimized analytically and the position of neuronal cell bodies is given by (26, 29, 30):

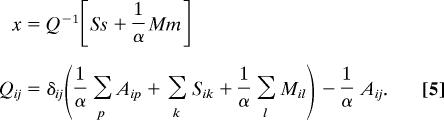Minimization of the quadratic cost function is mathematically identical to finding the equilibrium placement of objects connected with elastic rubber bands (minimum elastic energy of rubber bands with zero length at rest).

Comparison of the Minimum-Wiring Placement with Actual Layout

Using the complete connectivity diagram of the C. elegans nervous system, we calculate neuron positions that minimize the quadratic cost function (ζ = 2 in Eqs. 2 and 3, 1 < ζ < 4 to be considered later). Data sets are available at http://www.wormatlas.org/handbook/nshandbook.htm/nswiring.htm. Fig. 1C shows optimal neuronal layout in the one-dimensional worm, where neurons from the same ganglion are represented by the same color, offset vertically for clarity.

We compare this result to actual locations of neuronal cell bodies projected into one dimension along the anterior–posterior axis of the worm (Fig. 1B). Neurons belonging to the same ganglia are clustered (positioned near each other) in the actual layout. Wiring-cost minimization predicts somewhat more dispersed clusters of neurons located in the anterior two-thirds of the worm and no clustering for neurons in the tail ganglia (see Ganglia Distribution in Supporting Text and Fig. 5, which are published as supporting information on the PNAS web site). Later we will discuss possible causes for such discrepancies. Because a large number of the sensory organs are located in the tip of the head (34), aggregation of neurons in the anterior region of the animal is consistent with minimization of cost required to connect these sensors (20). The predicted anterior–posterior order of the first five ganglia, as defined by the median of neuron positions, agrees with the actual order. The actual ganglia ordering was previously obtained by Cherniak via brute force enumeration of all possible permutations (20). However, as mentioned previously, the method used to obtain Cherniak’s result cannot be applied at the level of individual neurons.

Next, we plot predicted positions of individual neurons as a function of actual positions in the worm (Fig. 2). Neuron locations in the animals are scaled between 0 and 1, where 0 is the head and 1 is the tail. The majority of neurons in the network lie along the diagonal of the plot, where predicted position equals actual position. On average, the cost-minimized neuron is located at 9.71% of the worm body length away from the actual location. Half of the predicted positions lie within 5.10% of their actual layout. The discrepancy between the mean and median of the distribution indicates that a small number of neurons account for the largest deviations. These “outlier” neurons will be analyzed further in the following sections.

Fig. 2.

Neuron positions predicted by the quadratic dedicated-wire model vs. actual neuron positions. (Upper) Positions are normalized by the worm body length (0 = head; 1 = tail). Perfect predictions fall on the diagonal. Circles of the same color represent cell bodies belonging to the same ganglion. Three classes of pioneer neurons are labeled. (Lower) Schematics depicting the progression of pioneer neurons during worm development. Arrows indicate direction of neurite growth.

To evaluate how well wiring-cost minimization predicts neuron position, we compare our results against a null hypothesis that more related neurons are positioned closer to each other. In C. elegans, the lineages of individual cells are reproducible and have been fully mapped (36, 37). By assuming that each cell division in the lineage tree reduces “relatedness” by one unit, we found the “relatedness” matrix between any two neurons in the nervous system (see Lineage Analysis in Supporting Text). Then we minimized the quadratic cost function with coefficients given by the “relatedness” matrix by substituting nonexistent external connection with a uniform repulsive force (26). The mean deviation from actual is 26.1%, a worse prediction than that generated by wiring minimization.

We also evaluate how well cost minimization is able to predict neuron position by comparing our results to a neuronal layout generated at random from a uniform distribution. Randomly placed neurons have a mean deviation from the actual position 34.6% and the median of 30.9%, both much greater than wire-minimized placement. Provided the distribution of the mean is Gaussian, the probability of obtaining an average deviation for 279 neurons better than the results from cost minimization is 10⁻⁶⁸. Therefore, wiring-cost minimization is a meaningful description of the relationship between neuronal arrangement and connectivity in the worm.

Despite reasonable agreement between predicted and actual layout, the total wiring cost of the actual network is almost four times greater than that of the optimized solution. Does this discrepancy arise from the cost of internal or external connections? The cost from neuron-to-neuron connections (C^int from Eqs. 1 and 2) makes up 91.7% of total cost in the actual worm. This value is 6.24 greater than the internal cost from the predicted layout. On the other hand, the ratio of actual to predicted external costs (C^ext from Eqs. 1 and 3) is significantly lower at 0.93. This result suggests that neurons in the actual layout are well positioned to minimize connections to external structures but are not fully optimized for neuron-to-neuron connections.

However, the total cost of the actual placement is still four times less than that of the randomly generated placement. In other words, the total cost ratio of optimized to actual to random layout is 1:4:16. Provided the distribution of cost for a random placement is Gaussian, the probability of obtaining a cost equal to or lower than the actual cost is 10⁻³³. Again, the significance of this metric suggests that the wiring-minimization approach gives nontrivial results.

Robustness of Optimization Results to Small Variations of Parameters

To determine the robustness of the wire-minimized solution, we explored several aspects of the cost function and assessed their impact on the ability to predict neuronal layout.

First, we analyze the sensitivity of the wire-minimized layout to the normalization coefficient α and the exponent ζ. As mentioned, our cost formulation accounts for multiple synapses on a given neurite by normalizing connection weights by the average number of synapses per neurite (α = 29.3). We test how the predicted layout changes by varying α between 1 and 45. Because the choice of the quadratic form of the cost function may seem arbitrary, we also varied the power of wire length in the cost function, ζ in Eqs. 2 and 3 between values of 1 and 4. As argued previously, the wiring cost is likely to scale supralinearly (ζ > 1) with distance between neurons (26). If so, the minimization problem is convex and can be efficiently solved numerically. The lowest mean deviation, 9.71%, is achieved by using the cost function with normalization coefficient ≈27 and exponent ≈2 (see General Power-Law Cost Function in Supporting Text and Fig. 6, which are published as supporting information on the PNAS web site). Interestingly, these values are close to those chosen from biological considerations and validate the quadratic cost function.

Second, we test the importance of synaptic multiplicity between neurons. Instead of a wire dedicated to each synapse between cells (Fig. 1C Inset), we use a single wire to connect a given pair of neurons regardless of the number of synapses (Fig. 1D Inset). In other words, we minimize the quadratic cost function with a binary connection matrix (only 0 or 1 elements in the matrix A from Eq. 2). Using ζ = 2, the lowest mean deviation between predicted and actual position (9.82%) is higher than the result from a synapse-number weighted cost function and was found at α = 8. In the actual worm, the average number of synaptic partners (as opposed to individual synapses) per neurite is 12.2, close to the optimal value of α obtained from the binary connection matrix.

To summarize, we find that various reasonable cost functions predict neuronal placement incomparably better than the random one. Although mean deviations vary somewhat between different cost functions, they are not far from the best known solution. Thus the wire length minimization approach is rather robust. Because the quadratic cost function can be solved exactly and is reasonably close to the best-known solution, it may serve as the reference predicted layout. Although the predicted placement is only approximately correct, we recall that the problem was solved in one dimension. Such dimensionality reduction may introduce errors on the order of the inverse aspect ratio of the worm, just under 10%. Because the mean deviations we report approach this range, wiring optimization results are encouraging.

What Causes Discrepancies Between Predicted and Actual Neuronal Layouts?

Several reasons may account for the deviation between positions predicted by wiring-cost-minimized and actual neuron positions. (i) The actual system is not fully optimized. (ii) The wiring diagram is still somewhat incomplete. (iii) The wiring cost function does not fully represent costs associated with neuronal placement, or constraints other than connectivity need to be taken into consideration. Although reason i remains a possibility, its exploration lies beyond the framework of the optimization approach (38). Reason ii can be addressed by future reconstructions. Here, we explore the merit of reason iii.

By taking a closer look at neurons with the greatest deviation between predicted and actual positions, we find that these “outliers” have common morphological features. Fig. 3A shows the histogram of differences between predicted and actual positions for neurons with cell bodies in the head, midbody, and tail of the animal. We define the head region by positions along the body axis <25% from the anterior of the worm, midbody is between 25% and 75%, and tail is >75% (see Neuron Position in Supporting Text). The top 10 outliers in the network are in the neuron classes PVQ, PVT, DVC, PVN, PVP, PVW, and PVC, all located in the tail of the worm. The biggest outliers in the head are AVA, AVG, and RID. In the midbody, SDQL, HSNL, and DA06 have the largest deviations. All of these neurons, except DA06, have long processes that span >25% of the worm body.

Fig. 3.

Analysis of cost-minimization outliers. (A) Histogram of absolute value of predicted-actual positions. (Top) Neurons with cell bodies in the head of the worm. (Middle) Neurons with soma in the midbody. (Bottom) Neurons with soma in the tail. Red vertical line in each plot marks the first standard deviation from the mean. Asterisks indicate neurons with ambiguous wiring (see text and Supporting Text for definitions). (B) Asymmetry of synapse position relative to the soma (1 = all synapses in the head and tail are located on opposite end of the worm as the cell body; 0 = all synapses in the head and tail are close to the cell body) vs. prediction error of wiring cost minimization. Bolded neurons above blue line (asymmetry >75%) are pioneer neurons. (C) Synaptic inputs near the cell body vs. prediction error of wiring cost minimization. Bolded neurons above the blue line (percent inputs >75%) are command interneurons for locomotion. The vertical red line is first standard deviation of wiring-cost model deviation.

Distribution of Synapse Locations Along a Neuron May Not Predict Cell Body Placement

Because most outliers have long processes spanning the worm body, could the constraints for cell body placement along the process be different from the dedicated wire model? Using the quadratic wiring cost, the dedicated wire model places the neuronal cell body at the weighted center of mass of the positions of its synaptic partners and fixed structures. Then, the cell bodies should not deviate too far from the center of mass location of their synapses.

We test whether actual cell body locations are consistent with synapse distribution along a neurite as expected from the dedicated-wire model. Because the position of synapses can be approximated only to within one-third of the worm body (see Synapse Position in Supporting Text), we consider long-reaching (>25% body length) neurons with cell body located in either the head or tail (109 neurons). Using an asymmetry factor defined by the percentage of head and tail synapses located on the same end of the worm as the cell body, we study how synapses distribute between head and tail. The asymmetry factor is 0 if all synapses are at the same end of the worm as the cell body. For neurons with 100% of head and tail synapses on the opposite end of the worm as the cell body, the asymmetry factor is 1.

We find all neurons with asymmetry factor >75% (above the blue line in Fig. 3B) are outliers in the wiring-minimized layout (right of the red line in Fig. 3B). This group of neurons includes all developmental pioneers of the ventral cord currently known in C. elegans: AVG, PVPL/R, and PVQL/R. By comparing the positional deviations of known pioneers with the deviations of the rest of the neurons in the system, we find that all pioneers are outliers in the wire-minimized layout (significant for pioneers as a group, P = 0.002 from Student’s t test). The most prominent anterior outlier, AVG, is born in the head (39). During development, the neuron sends the first posterior-directed projection into what eventually becomes the right ventral cord, pioneering a path for other anterior neurons to follow (Fig. 2). Along the way, AVG makes synapses with neurons in the midbody and the tail. Neurons PVP and PVQ, the biggest outliers in the tail, behave similarly but in the reverse direction: they are born in the tail and send pioneering processes forward. Ablation of these pioneer neurons results in disorganization of ventral cord fascicles, although a nerve cord is still formed (39). All of these pioneer neurons are characterized by long processes that span the entire length of the worm with the majority of synapses situated outside of the soma region.

Another key player in neural development, PVT, also has synapses mostly on the opposite end of the worm from the soma. The previously published wiring of PVT (34) was later amended (O. Hobert and D.H.H., unpublished work). Interestingly, only after these changes are incorporated does PVT emerge from this outlier analysis. Functionally, PVT acts as a guidepost cell for neurons located in the posterior region of the worm to grow forward (40, 41) and maintains the organization of ventral cord fascicles (42). Without PVT, axons in the lumbar ganglia fail to enter the ventral cord in a single bundle, and axons already in the ventral cord cross the ventral midline in an aberrant manner.

The remaining neurons with asymmetry factor >75%, DVC and PVR, are also outliers in the wire-minimized solution and, based on their structural characteristics, we propose that DVC and PVR may also play pioneering or developmental roles. PVR, an interneuron located in the lumbar ganglion, is a putative tail sensory neuron, with some animals displaying microtubule bundles in the posterior process (34, 35). The pioneering role of DVC has been previously postulated by Durbin (39) by using independent data. However, this hypothesis was not fully verified by experiments (39).

Directionality of Synapses Along the Neuron May Bias the Location of Cell Bodies

Because analysis of synapse position relative to the cell body does not account for all outliers, such as AVA and PVC where synapses are evenly distributed, we hypothesize that the directionality of synapses might be important. We found an asymmetry in the spatial distribution of pre- and postsynaptic terminals for AVA and PVC (Fig. 4). Specifically, the region containing cell bodies of these neurons contains more inputs or post- than presynaptic terminals. This unexpected result suggests that the distance between cell bodies and pre- vs. postsynaptic terminals invokes different connection costs. Because the dedicated-wire model does not distinguish between the location of individual synapses or the type of synaptic terminals, the failure of our cost minimization to predict the actual position of these neurons is not surprising.

Fig. 4.

Distribution of synapses by directionality and type along command interneurons. Neuronal outputs or presynaptic terminals are shown in blue, inputs or postsynaptic terminals are shown in red, and electrical junctions are shown in green. (Upper) AVAL. (Lower) PVCR.

By examining the type of synapses near the soma of neurons with long projections and >25% of head/tail synapses near the cell body (101 neurons), we find a small group of 12 neurons with predominately postsynaptic terminals (>75%) near the cell body (above the red line in Fig. 3C). With the exception of AVEL/R, all of these neurons are either outliers (AVAL/R, DVA, and PVCR) or very close to being outliers (AVBL/R, AVDL/R, and AVL). Within this group, AVEL/R are the only neurons that do not have neurites spanning the entire length of the worm; their cell bodies are in the head, and neurites project halfway down the worm, terminating anterior to the vulva. The shorter span might be the reason why AVEL/R do not emerge as outliers.

The directionality of synapses (input or output) near the cell body is a structural property capable of identifying neurons important for integrative signaling in motor control. The collection of neurons with mostly inputs near the soma includes all, except PVCR, of the command interneurons (nine neurons) functionally identified as responsible for worm locomotion (43, 44). Wild-type worms, when touched on the head, respond by moving backwards. Without AVA, AVD, and AVE, worms no longer exhibit this behavior. AVB and PVC are responsible for the exact opposite response; they mediate forward movement when worms are stimulated at the tail.

Although neurons in C. elegans appear isopotential and do not generate classical Na⁺ action potentials (45), command neurons may have special requirements to reach an activation threshold near the cell body before a command signal can be passed along the process to distant targets. Physiological study will be necessary to understand the underlying mechanism for the position of pre- vs. postsynaptic terminals relative to the cell body.

The analysis of asymmetry in directionality of synapses revealed noncommand neurons that appear to mediate motor functions. DVA, presynaptic to command interneurons and forward locomotion motor neurons, is involved in mechanosensory responses (46). When subject to a diffused mechanical stimulus, such as a disturbance (e.g., tap) of the substrate on which the worm is resting, the worm responds by moving either forward or backward. Without DVA, the acceleration of such movement is diminished. AVL, acting in conjunction with neuron DVB, is critical for activating muscle contraction for defecation (47). RID has unknown function although both AVL and RID make neuromuscular connections to body muscles.

Wiring Optimization Using the Shared-Wire Model

To incorporate the importance of synapse location and directionality into theory, we propose an anatomically more accurate shared-wire model (Fig. 1E Inset). In this model, each neuron is represented by a wire with multiple synapses. If a pair of neurons is synaptically connected, the corresponding wires must overlap. Similarly, if a neuron makes an external connection, the corresponding wire must include the location of that fixed point. Given these constraints, minimization of total wiring length (31, 33) yields the optimal placement of each synapse as well as the front and back ends of each neuron.

Because the actual locations of most synapses in the worm are not currently known, comparison with data requires predicting cell body positions. One possibility is to assign the cell body position to the center of mass of synaptic locations for each neuron. If connections are treated equally (analogous to the binary dedicated-wire model), the mean deviation of the predicted cell body location is 10.6% from actual. If connections are weighted by their multiplicity (number of synapses per connection analogous to the weighted dedicated-wire model), the mean deviation is 10.7%. In either case, the accuracy of the shared-wire model is no better than the dedicated-wire model.

However, the shared-wire model allows us to apply the results from outlier analysis by adopting different rules for the placement of cell bodies in neurons with specialized functions. First, we incorporate the observation that cell bodies of command interneurons gravitate toward postsynaptic terminals. For these neurons, the cell body is placed at the end of the neuron closest to the center of mass of postsynaptic terminals. Second, we incorporate the observation that cell bodies of neurons important in developmental pioneering are located on the opposite end of the neuron from the majority of synapses. For these neurons, we consider only the synapse-containing region (excluding connections to external structures). The cell body is placed at the end of this region most distant from the synaptic center of mass. Applying these rules for specialized neurons to the distribution of synapses obtained in the shared-wire model, we obtain a placement (Fig. 1E, Shared-Wire Model in Supporting Text and Fig. 7, which are published as supporting information on the PNAS web site) with mean deviation of 9.41%, better than predictions from the quadratic dedicated-wire model.

Wiring optimization using the shared-wire model makes an interesting prediction where a large fraction of all synapses congregates in a single anterior location along the worm (Fig. 7 Lower). It is natural to associate this location with the nerve ring. Of course, because our model is 1D, the actual 3D structure of the nerve ring could not emerge. Yet, this congregation of synapses is an unexpected demonstration of the predictive power of wiring optimization.

Discussion

Here we show that wiring minimization can establish a relationship between neuronal structure and function. We found that, for given connectivity, wiring optimization predicts the layout of many neurons in the animal despite some uncertainty about the exact form of the wiring cost. Thus, wiring optimization is a constructive approach for relating wiring diagram and neuron placement. Detailed comparison of the wiring optimization prediction and actual layout reveals neurons with special structural properties that have specialized function. Therefore, wiring optimization may also be used for predicting neuronal function.

Although wiring optimization establishes a structure–function relationship, there could be other factors affecting neuronal placement. In particular, we were unable to fully explain the placement and clustering of neurons belonging to the tail ganglia. In addition to the causes considered in the paper, other constraints could account for these discrepancies. For example, nonsynaptic communication between neurons via neuromodulators or paracrine signaling is not accounted for by wiring cost minimization. In principle, these constraints could be incorporated into the model if we knew which neurons participate in such signaling and the cost function. Also, we ignored the volume exclusion effect, which could push neurons away from their optimal positions (14). Finally, absence of clustering and relatively forward placement of the tail ganglia may be due to incomplete or ambiguous wiring data for posterior neurons (34).

Given that positions of neurons are optimized for specified functional constraints, what underlying biological mechanisms are responsible for such optimization in C. elegans? Experimental evidence suggests that wiring minimization may be driven by genetics as well as forces generated during embryonic and postembryonic development. Studies that support evolutionary mechanisms show that the position of synapses can be perturbed without affecting cell body position and vice versa (48). The identification of pioneers in the outlier analysis also demonstrates the importance of genetics in neuronal layout. Furthermore, a few neurons in the worm migrate long distances during development to positions where connection costs are lower than their initial positions (data not shown) (49). However, mutant worms with miswired neurons demonstrate both wild-type as well as displaced cell body positions (50, 51). This displacement could result from tension in neurites demonstrated in vivo (52) and in vitro (53, 54). Such tension may pull connected cells closer together and optimize the layout during development (55). We hope that future research will contribute to the field of evolutionary developmental biology by shedding light on the interplay between developmental mechanisms and genetic information in specifying neuronal position (56).

In conclusion, we show that neuronal layout can be largely predicted by minimizing the wiring cost for given synaptic connectivity. The discrepancy between optimized and actual placement is mainly due to neurons with stereotypical roles in the network, such as developmental pioneers and command interneurons. This discrepancy may be due to the specialized requirements on synapse placement relative to cell body. Although wiring optimization may not be the only factor in neuronal placement, it is the only one that has been quantified and has predictive power to relate neuronal structure and function.

Note added in proof.

After completion of this work, we became aware of two related studies (57, ¶) .