Variation in External Rotation Moment Arms among Subregions of Supraspinatus, Infraspinatus, and Teres Minor Muscles

Abstract

A rotator cuff tear causes morphologic changes in rotator cuff muscles and tendons and reduced shoulder strength. The mechanisms by which these changes affect joint strength are not understood. This study’s purpose was to empirically determine rotation moment arms for subregions of supraspinatus, infraspinatus, and for teres minor, and to test the hypothesis that subregions of the cuff tendons increase their effective moment arms through connections to other subregions. Tendon excursions were measured for full ranges of rotation on 10 independent glenohumeral specimens with the humerus abducted in the scapular plane at 10 and 60°. Supraspinatus and infraspinatus tendons were divided into equal width subregions. Two conditions were tested: tendon divided to the musculotendinous junction, and tendon divided to the insertion on the humerus. Moment arms were determined from tendon excursion via the principle of virtual work. Moment arms for the infraspinatus (p < 0.001) and supraspinatus (p < 0.001) were significantly greater when the tendon was only divided to the musculotendinous junction versus division to the humeral head. Moment arms across subregions of infraspinatus (p < 0.001) and supraspinatus (p < 0.001) were significantly different. A difference in teres minor moment arm was not found for the two cuff tendon conditions. Moment arm differences between muscle subregions and for tendon division conditions have clinical implications. Interaction between cuff regions could explain why some subjects retain strength after a small cuff tear. This finding helps explain why a partial cuff repair may be beneficial when a complete repair is not possible. Data presented here can help differentiate between cuff tear cases that would benefit from cuff repair and cases for which cuff repair might not be as favorable.

INTRODUCTION

Joint torque produced by muscle force is in direct proportion to the muscle’s moment arm. Rotator cuff tear causes morphologic changes to the cuff’s muscles and tendons ^1–4 that can alter the mechanical performance of the joint by decreasing joint stability.^5–7 Additionally, shoulder rotation strength is known to decrease following rotator cuff tears.^8–11 One mechanism by which rotator cuff tear can affect joint strength is alteration of muscle moment arms. The altered moment arms may occur in the involved muscle–tendon or in adjacent muscle–tendons not directly involved in the tear, because the rotator cuff is a contiguous tissue where tendon excursions and muscle forces are transferred across adjacent tendons and tendon subregions. With rotator cuff tear, tendon excursions can be reduced and moment arms decreased.

Glenohumeral rotation moment arms have been determined empirically in previous studies.^12–14 Bassett et al. measured moment arm data in five specimens with the shoulder in the 90° abduction and 90° external rotation by taking serial cross-sections of the joint and geometrically determining distances from joint center to muscle centroids. Kuechle et al. measured instantaneous moment arms via the tendon excursion method in 10 specimens in four elevation positions. In these two studies, rotator cuff muscles were considered as one linear unit from the muscle origin to the muscle insertion, instead of considering the contributions of these muscles at the suborgan level. Otis et al. determined moment arms via tendon excursion and joint rotation data in 10 specimens for multiple positions of abduction and rotation. The infraspinatus was divided into three portions, the supraspinatus into two portions, and the teres minor was treated as having one path. They did not find a significant difference between moment arms of the infraspinatus subregions, but did find a significant difference between the anterior and posterior supraspinatus moment arms.

These studies did not examine the interaction between portions of the rotator cuff, or between subregions of cuff tendons. Because the rotator cuff muscles insert into the broad tendinous cuff rather than directly into the humerus through individual tendons, we believe that an interaction between subregions increases the moment arms of each region. This interaction is clinically relevant for two reasons. First, tears can occur in one or more subregions, leaving only a portion of the muscle still attached. The functional effect of a subregion tear might be reduced through transfer of force through adjacent intact cuff attachments. Second, tendon transfers may be performed to repair or alter the torque generating capacity of rotator cuff muscles. By definition, these transfers require removal of tendons and disruption of the rotator cuff. The mechanisms by which these tears or transfers affect excursion of adjacent tendons or subregions and the moment arms are not well understood.

The purpose of this study was to empirically determine rotation moment arms for subregions of infraspinatus, supraspinatus, and teres minor. The hypotheses for our study were twofold. First, that these muscles possess differences in moment arm due to joint angle and muscle subregion. Second, that subregions of the cuff tendons increase their effective moment arms through connections to other subregions. The moment arms measured here increase our understanding of muscle action at submuscle–tendon level and increase our understanding of the mechanical changes associated with rotator cuff tears.

MATERIALS AND METHODS

Glenohumeral rotation moment arm data were collected from 10 independent unembalmed human cadaver humerus–scapula extremities obtained from anatomical donations. Cuff integrity and condition was inspected by dissecting all tissue superficial to the rotator cuff. Specimens with severe arthritis, rotator cuff tears, or abnormal muscle or bone anatomy were not included. Prior to testing the upper extremities, anthropometric measurements were made on the cadavers (Table 1). Specimens were a convenience sample of seven males and three females (average age was 72 years). On individual cadavers, side was randomly selected by coin toss. Scapula length was the distance from the acromio-clavicular joint to the inferior angle of the scapula. Humerus length was measured from the most superior point on the humeral head to the most inferior point on the humerus.

Table 1.

Cadaver Anthropometric Parameters

Specimen (Gender)	Height (m)	Weight (kg)	Scapula Length (AC-AI) (cm)	Humerus Length (cm)
1 (F)	1.68	50.0	17.0	31.1
2 (F)	1.63	61.4	15.6	27.4
3 (M)	1.78	58.6	17.6	29.7
4 (M)	1.75	97.7	21.7	35.8
5 (M)	1.73	60.9	20.2	37.1
6 (M)	1.96	122.7	20.7	36.7
7 (M)	1.88	118.2	19.8	33.5
8 (M)	1.57	100.0	20.5	36.4
9 (M)	1.75	109.1	19.7	32.7
10 (F)	1.68	77.3	18.6	30.9

Specimens were frozen at −20°C for approximately 2 weeks. Specimens were thawed in a room temperature water bath 24 h prior to dissection. Specimens were prepared by blunt dissection of all muscles and tissue superficial to the rotator cuff. A hole aligned with the axis of the humeral epicondyles was drilled in the proximal humerus 2 cm distal to the humeral head. A threaded rod was rigidly fixed to the humerus through this hole, and later used to rotate the specimen. The humerus was then transected 1 cm distal to the deltoid tuberosity. An intermedullary PVC rod was threaded into the humerus and rigidly locked with two screws perpendicular to the humerus. PVC rods were of diameter 3/8 inch, 1/2 inch, or 5/8 inch to match the intermedullary diameter. An acrominectomy was performed to access the supraspinatus and allow for routing of cords approximating supraspinatus morphology. The coracohumeral ligament was preserved. Careful dissection was used to identify rotator cuff muscle origins and to elevate muscles from their respective origins. Tendon width and muscle belly width at the widest point of supraspinatus and infraspinatus were measured with a digital caliper. Tendon and muscle were then dissected into three and four equal width portions for the supraspinatus and infraspinatus, respectively. The teres minor was dissected as one unit.

Muscles were then dissected from tendon at the musculotendinous junction, and measurements for estimating the force-generating capacity of the muscles (physiologic cross-sectional area, pennation angle, and force-length dependence) were recorded.^15,16 The subscapularis tendon was divided into two equal portions. Each muscle subregion was treated as an individual muscle for moment arm measurement. Twelve-pound test fishing line was sutured to each tendon stump. For each muscle subregion, custom cord guides determining muscle subregion origins were located at the spinoglenoid notch. A second set of guides routing cords to potentiometer pulleys were attached along the medial border of the scapula. Guides were located by measuring the circumferences of the supraspinatus and infraspinatus fossa, dividing each fossa into three and four equal circumferential regions, respectively. Holes were drilled in the scapula, and the guides screwed into bone so that guide locations were coincident with centroids of each third of the supraspinatus and each fourth of the infraspinatus.

A custom-fabricated instrument was designed and used to measure the change in tendon excursion relative to humeral head rotation (Fig. 1). The instrument was calibrated with PVC rods representing phantom humeral heads of known fixed and varying radii. The difference in measured and actual radii of the phantom heads was < 0.5 mm. Following preparation, specimens were mounted to the instrument with a clamp to secure the scapula, and the cords were wrapped around pulleys attached to 10 turn potentiometers (3500S-2-103, Bourns Corp., Riverside, CA; linearity tolerance −0.2%) that were calibrated to ensure linearity and aligned so that potentiometer end points were not reached during each trial. The humeral intermedullary rod was attached to a one-turn potentiometer that measured humeral rotation. Potentiometers were powered by a 10-V power supply. Masses of 250 g were attached to the cords. Stretch of the cords during excursion occurred in a linear elastic nature. This relationship was the same for all muscles/cords, and was measured and accounted for during data analysis. Cords were also sutured to subscapularis tendon stumps and routed over a low-friction pulley. Subscapularis tendons were weighted with 750-g masses whose size was determined from earlier data¹³ and pilot testing as that necessary to maintain static equilibrium at all rotation angles. The humeral head was moistened with saline. All trials were 10 s duration, and data were collected at 30 Hz with an analog–digital converter (Measurements Computing Corp., Middleboro, MA) using LabView (National Instruments Corp., Austin, TX) virtual instrument software.

Figure 1.

Tendon excursion–rotation angle measuring instrument with specimen mounted at 60° abduction in the scapular plane.

Rotation moment arms were measured at two positions of abduction in the scapular plane, 10° and 60° of glenohumeral abduction using the tendon excursion versus joint angle method. These two positions simulated the positions of neutral abduction and 90° of humeral abduction, based on previous reports describing glenohumeral motion and scapular position relative to the thorax.^17,18 Rotation moment arms were measured for both positions for two conditions: tendon divided in a medial to lateral direction just to musculotendinous junction (intact cuff condition, Fig. 2A), and tendon further divided laterally to the ultimate insertion on the tuberosities or humeral head (divided cuff condition, Fig. 2B). These conditions were used not to simulate cuff tears, but to determine how tears that occur along and between cuff tendons affect the excursions and moment arms of adjacent tendons.

Figure 2.

Cuff tendon conditions. The humeral head is depicted with rotator cuff tendons and cords sutured to the tendons for the two cuff conditions. The acromion is at the left of each image. (A) Intact cuff condition. Tendon divided just to musculotendinous junction. (B) Divided cuff condition. Tendon further divided to the ultimate insertion to bone on the humeral head. Divisions denoted with dotted lines.

The specimens were carefully aligned in the scapular plane, and the abduction angle set with a goniometer. Neutral rotation was defined by aligning the rod aligned with the humeral epicondyles with the scapular plane. Maximum internal and external rotation was found by rotating the specimen and observing the maximum possible rotation that maintained humeral head–glenoid contact. Voltages across the humeral rotation potentiometer were observed and recorded to ensure trials were initiated and completed at the same angles. Following testing for the intact condition, tendons of the respective muscles were divided to the insertion on the humeral head. Specimens were retested for the divided condition at 10 and 60° abduction angles. Three trials were performed at each position and condition.

Tendon excursions versus joint angles were plotted for the three trials of a given abduction angle and condition, and moment arms determined.^13,14,19 Polynomials of second through sixth order were fit to the data. Higher order polynomials resulted in fitted excursions that did not match measured excursions for the initial and final portions of the data. For each independent muscle of each specimen, the order of polynomial that minimized root-mean-square error between measured and fitted excursions was selected. Derivatives of the tendon excursion versus joint angle relationships were determined analytically to calculate moment arms²⁰ via the principle of virtual work (Fig. 3). Moment arms were determined by evaluating the derivatives at 1° increments through the arc of rotation.

Figure 3.

Superior–inferior view of the humeral head depicting excursion of the infraspinatus tendon with increasing external rotation. The moment arm is the instantaneous derivative of the tendon excursion to joint angle relationship.

Data analysis and reduction were performed using MatLab 6.5 (Mathworks, Natick, MA). Statistical analysis was performed with SYSTAT 10.2 (Systat Software, Inc., Point Richmond, CA). For infraspinatus and supraspinatus, four-way analysis of variance (ANOVA) models were used to test the effect of abduction angle (10 and 60°), rotation angle (10 levels in 15° increments from 45° internal rotation to 90° external rotation), cuff condition (intact and divided), and muscle subregion (four and three levels, respectively) on moment arm. For teres minor, a three-way ANOVA was used to test the effect of abduction angle, rotation angle, and cuff condition (same levels) on moment arm. In each case, specimen was a blocking variable to account for inter-specimen variability. Data were presented as mean and standard deviation.

RESULTS

Abduction angle, rotation angle, cuff condition, and muscle subregion had significant effects on rotation moment arm of infraspinatus (Figs. 4A, 5A and 6A) and on the supraspinatus moment arm (Figs. 4B, 5B and 6B). For teres minor, abduction angle and rotation angle had a significant effect on moment arm (Fig. 4C), but the condition of the cuff did not significantly affect moment arm (Fig. 5C). (Summary statistics for moment arms for all tendon conditions and joint angles are submitted as a separate document for electronic linking to this article.)

Figure 4.

Rotation moment arms (mean ± SD) as a function of external rotation angle at 10° and 60° abduction. (A) Infraspinatus demonstrated a greater change in moment arm at 10° abduction compared to 60° abduction (p < 0.001). (B) Supraspinatus also demonstrated a greater change in moment arm at 10° compared to 60° (p < 0.001). (C) At 10° abduction teres minor moment arm increased as the shoulder was externally rotated. Conversely, at 60° abduction teres minor moment arm decreased with increasing external rotation (p < 0.001).

Figure 5.

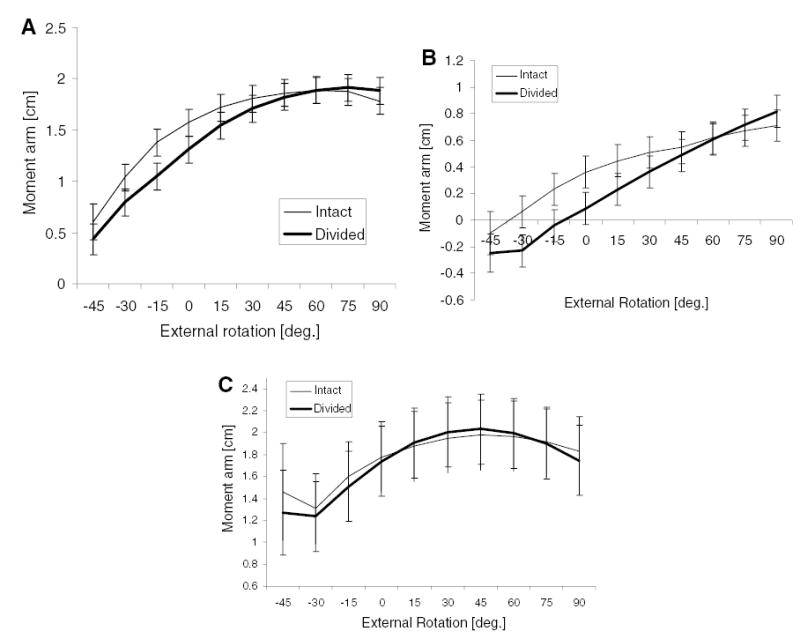
Rotation moment arms (mean ± SD) as a function of external rotation angle for the intact and divided tendon conditions. (A) Infraspinatus moment arm was reduced for the divided cuff condition at rotation angles less than 30° external rotation (p < 0.001). (B) Supraspinatus moment arm was also reduced for the divided cuff condition at less than 30° external rotation (p < 0.001). (C) For teres minor, the division of the cuff did not significantly affect moment arm (p = 0.46).

Figure 6.

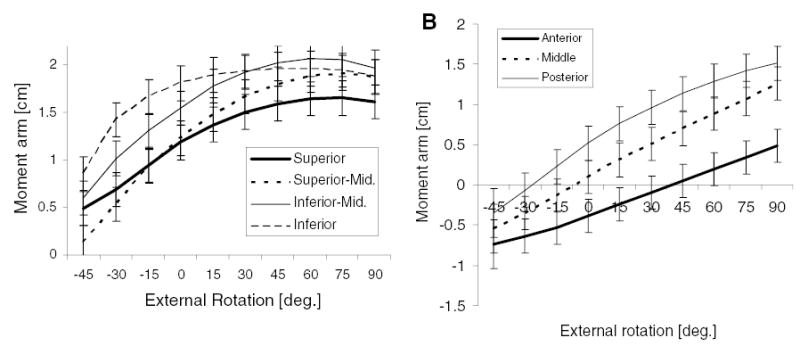
Rotation moment arms (mean ± SD) as a function of external rotation angle across muscle subregions. (A) Infraspinatus moment arms were significantly different across subregions (p < 0.001). With increased external rotation, moment arms for the superior and inferior subregions did not continually increase as much as moment arms for the two middle subregions. (B) Supraspinatus moment arm increased from the anterior, to middle, to poster subregions (p < 0.001).

Infraspinatus moment arm increased with increasing rotation angle (p < 0.001). Average moment arm across subregions was greater at 10° (1.72 ± 0.03 cm) versus 60° (1.27 ± 0.031 cm) abduction (p < 0.001) (Fig. 4A). Infraspinatus demonstrated a greater change in rotation moment arm at 10° compared to 60° abduction (p < 0.001). Consequently, moment arms at positions of 15° and greater internal rotation were smaller at 10° than 60° abduction. Conversely, at positions of neutral and external rotation, moment arms were larger.

Average moment arms of supraspinatus subregions (p < 0.05) were significantly greater at 60 (0.37 ± 0.03 cm) compared to 10° (0.41 ± 0.03 cm) abduction, although this small difference is not clinically significant. At 10° abduction, supraspinatus contributed to external rotation at positions of increased external rotation, but at 60° abduction supraspinatus was an agonist for external rotation at all rotation angles. Supraspinatus rotation moment arms were larger for an increased external rotation angle (p < 0.001). However, the effects of rotation angle were modified by a significant interaction (p < 0.001) with abduction angle resulting in moment arms that remained relatively constant with increasing rotation angle at 60° abduction (Fig. 4B). Subregions of supraspinatus at 10° abduction were antagonists for external rotation when at internally rotated joint angles (Fig. 4B). Then, as joint angle increased (external rotation), the subregions became agonists for external rotation. These muscle subregions were initially anterior to the rotation axis, and thus lengthened during external rotation. Then, with increased external rotation the muscle path changed relative to the axis of rotation, such that the muscle subregions could shorten and contribute to external rotation.

Average moment arm of teres minor (p < 0.001) was significantly greater at 60° (1.94 ± 0.09 cm) compared to 10° (1.56 ± 0.09 cm) abduction (Fig. 4C). This contrasted with infraspinatus, perhaps indicating a naturally determined interaction between these two muscles. Teres minor moment arm was significantly larger (p < 0.001) with increasing rotation angle. Abduction of 60° caused an initially large moment arm that decreased slightly with increasing rotation (Fig. 4C), resulting in significant interaction (p < 0.001) between abduction angle and rotation angle.

Division of the rotator cuff and tendon subregions resulted in a significant (p < 0.001) reduction in average infraspinatus moment arm across subregions (1.44 ± 0.03 cm) as opposed to an intact cuff (1.55 ± 0.03 cm). A divided cuff decreased moment arm more at internally rotated positions than at external rotation (Fig. 5A). Like infraspinatus, moment arms of supraspinatus (p < 0.001) were smaller for the divided (0.28 ± 0.03 cm) versus intact condition (0.41 ± 0.03 cm) (Fig. 5B). We did not find a difference (p = 0.46) in teres minor moment arm for the intact versus divided cuff condition (Fig. 5C).

Average moment arms of infraspinatus muscle subregions, superior (1.27 ± 0.06 cm), superior-middle (1.35 ± 0.06 cm), inferior-middle (1.63 ± 0.06), and inferior (1.73 ± 0.06 cm), were significantly (p < 0.001) different (Fig. 6A). Average moment arms of supraspinatus subregions, posterior region (0.60 ± 0.06 cm), middle (0.38 ± 0.06 cm), and anterior (0.05 ± 0.06 cm), were significantly (p < 0.001) different (Fig. 6B).

DISCUSSION

Our objective was to determine the rotation moment arms for subregions of infraspinatus and supraspinatus and for teres minor. We generated data for use in computational models of the musculotendinous elements crossing the glenohumeral joint. Most importantly, we provided estimates of instantaneous moment arms, which are required for predicting torques resulting from muscle forces.

Interestingly, muscle subregion significantly affected rotation moment arm for infraspinatus and supraspinatus. The differences in moment arms between subregions and for different cuff conditions may have clinical implications for differentiating between those subjects who retain strength with partial rotator cuff tear and those who do not function as well, or similarly between those patients who might benefit from cuff repair and those for whom results of cuff repair might not be as favorable. Additionally, moment arms were greater with an intact rotator cuff as opposed to a divided cuff. The divided tendon is underconstrained, and can find the path that minimizes or reduces excursion and moment arm. The clinical significance of this finding is that in the presence of a rotator cuff tear that does not involve an entire muscle, these cuff muscles have less ability to generate joint torque in the remaining muscle–tendon tissue due to altered force transmission and tendon excursion sharing. Given that some loss of strength seen clinically with isolated supraspinatus tears is in part due to muscle inhibition or pain, this finding might explain why supraspinatus tears are often associated with a decrease in external rotation strength despite the small external rotation moment arm. With loss of load transmission through an intact shared cuff insertion, the infraspinatus moment arm is decreased due to a supraspinatus tear. Furthermore, repair of even a portion of a cuff tear could result in greater recovery of external rotation strength than would be predicted based on the potential of that subregion alone.

Infraspinatus demonstrated little change in moment arm through the arc of rotation at 60° abduction compared to relatively large moment arm change at 10° abduction. Mechanically, this observation makes sense, because with the humerus in the 10° abducted position, the muscle–tendon path is at some joint angle nearly orthogonal to the axis of rotation. At this angle, a given change in humeral rotation will result in maximal tendon excursion, and hence, maximal moment arm. At all other joint angles a given humeral rotation will result in smaller tendon excursion and reduced moment arm. With the humerus abducted at 60° the muscle–tendon path is not orthogonal to the axis of rotation. Consequently, moment arm remains relatively constant throughout the arc of rotation.

Our data compare favorably with those of Otis et al.¹⁴ We also found that all subregions of supraspinatus at 10° abduction were internal rotators at positions of internal rotation, and only became external rotators at rotation angles greater than neutral. Also, all supraspinatus subregions were slight agonists for external rotation for all rotation angles at 60° abduction. In contrast to Otis et al., however, we found a difference in infraspinatus rotation moment arm between subregion for some positions. Additionally, the increase in infraspinatus moment arm with external rotation was greater for superior middle and inferior middle subregions than for the superior or inferior subregions. Teres minor was found to have a comparable moment arm with infraspinatus, but in contrast to Otis et al., increased abduction decreased teres minor moment arm while infraspinatus moment arm was less affected and remained relatively constant. Like Otis et al., we found substantial interaction effects between joint posture, muscle subregion, and, for our study, cuff condition. Otis and colleagues did not consider how condition of the rotator cuff affected moment arm. Our study increases understanding of how cuff condition affects tendon excursion, moment arm, and external rotation strength.

Biomechanical models require information relating moment arm as a function of joint angle to predict joint torque.^21,22 For simplicity, these models use data from previous studies to describe this relationship. Most previous studies provided moment arm data for the muscle as a whole even for broad, multipennate muscles with varying lines of action across the muscle and potentially varying moment arm. A strength of our study was that moment arms were measured for subregions of infraspinatus and supraspinatus. Excursions for the cuff tendons for subregions of muscles with broad origins and insertions were determined. The rotator cuff possesses contractile force generating tissue consisting of varying pennation and multiple force directions.^23–27 Models that lump the subregions as one muscle unit lack fidelity in representing a muscle’s force and moment generating ability.

A limitation is that specimens were rotated by hand, and the resulting kinematics might not exactly replicate in vivo motion. However, the instrument for measuring tendon excursion allowed for physiologic translation and rotation of the humeral head within the glenoid. Such an allowance reduces kinematic errors resulting from excessive constraints that might cause unnatural motion of the humeral head relative to the glenoid.

Despite these limitations, the tendon excursion technique was used to measure rotational moment arms for 10 specimens and provides information concerning the mean and variability of these parameters. This study is an attempt to capture the effects of some anatomical and morphological factors, as well as variability of these factors, on muscle–tendon excursion and moment arm.