Skip to main content
NCBI home page
Genome Research logoLink to Genome Research
. 2002 Jan;12(1):37–46. doi: 10.1101/gr.205602

Relating Whole-Genome Expression Data with Protein-Protein Interactions

Ronald Jansen 1,4, Dov Greenbaum 2,4, Mark Gerstein 1,3,5
PMCID: PMC155252  PMID: 11779829

Abstract

We investigate the relationship of protein-protein interactions with mRNA expression levels, by integrating a variety of data sources for yeast. We focus on known protein complexes that have clearly defined interactions between their subunits. We find that subunits of the same protein complex show significant coexpression, both in terms of similarities of absolute mRNA levels and expression profiles, e.g., we can often see subunits of a complex having correlated patterns of expression over a time course. We classify the yeast protein complexes as either permanent or transient, with permanent ones being maintained through most cellular conditions. We find that, generally, permanent complexes, such as the ribosome and proteasome, have a particularly strong relationship with expression, while transient ones do not. However, we note that several transient complexes, such as the RNA polymerase II holoenzyme and the replication complex, can be subdivided into smaller permanent ones, which do have a strong relationship to gene expression. We also investigated the interactions in aggregated, genome-wide data sets, such as the comprehensive yeast two-hybrid experiments, and found them to have only a weak relationship with gene expression, similar to that of transient complexes. (Further details on genecensus.org/expression/interactions and bioinfo.mbb.yale.edu/expression/interactions.)

Analysis of gene expression data is currently one of the most exciting areas in genomics. Computationally, it involves clustering and grouping individual expression measurements and interrelating them to other sources of information, such as phenotypes, functional classifications, or cellular responses (Golub et al. 1999; Brown et al. 2000; Califano et al. 2000; Gaasterland and Bekiranov 2000; Raychaudhuri et al. 2001; Subrahmanyam et al. 2001). In particular, functional assignment of uncharacterized genes can take place through transferring the annotation from a characterized gene (gathered from databases such as the catalog of the Munich Information Center for Protein Sequences (MIPS) or Gene Ontology (Ashburner et al. 2000; Mewes et al. 2000)) to an uncharacterized gene when their expression profiles are strongly related by a similarity criterion (such as the correlation coefficient). While this procedure is usually not sufficient to unambiguously determine the function of an uncharacterized gene, it can be the starting point (e.g., in target selection) for further genetic experiments, functional characterization, or high-throughput proteomic analysis (Luscombe et al. 1998; Westhead et al. 1999; Christendat et al. 2000a,b; Eisenberg et al. 2000; Emili and Cagney 2000; Gerstein and Jansen 2000).

An important component of functional annotation is characterizing protein interactions, as these often circumscribe (or effectively define) protein function. Moreover, protein interactions can be described more precisely than protein functions. Thus, rather than directly dealing with the general relationship between protein function and expression, we look here at a subproblem: the relationship between mRNA expression and protein-protein interactions, especially those in protein complexes. A priori it seems reasonable that there should be a well-defined relationship between the expression levels of the subunits in a complex: because the functionality of many complexes hinges on the presence of all the subunits, a haphazard and independent expression of any one subunit would be energetically costly. For instance, the components of the ribosome are regulated in a complex way but there is usually agreement that they should be present in equimolar amounts, although this has not yet been measured directly (Woolford et al. 1991; Planta et al. 1997; Li et al. 1999; Nomura 1999).

We investigate this relationship for many of the known protein complexes in a comprehensive, global fashion by interrelating many of the yeast data sets for protein interactions and expression. The diversity and number of yeast experiments provide high-quality data under varied conditions. Additionally, we investigate the relationship between other types of protein-protein interactions (e.g., aggregated physical and genetic interactions) and mRNA expression. Our work follows up on many recent analyses of protein-protein interactions (Fellenberg et al. 2000; Hishigaki et al. 2001; Teichmann et al. 2001; Walhout and Vidal 2001).

In general, our goal was to integrate and cross-correlate already existing data from different sources and find general trends in it. This is an exploratory study prior to any type of prediction. In a sense, this study can be understood as an exploration of the knowledge already implicit in the current data but not yet obvious because, previously, it has not yet been integrated and put together in this way.

RESULTS

In our survey of existing data, we used two different approaches to analyze the two different types of expression data available: the computation of normalized differences for absolute expression levels and a more standard analysis of the correlation of profiles of relative expression levels (expression ratios). We explain these two approaches in more detail in the following two sections.

Calculation of Normalized Differences between Absolute Expression Levels

To compare absolute mRNA expression levels between subunits of a protein complex, we define the normalized difference Dij as follows:

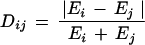graphic file with name M1.gif

where Ei and Ej are the mRNA expression levels of subunits i and j. This quantity defines the difference as a fraction of the sum of the expression levels, thus allowing for a comparison of gene pairs of both high and low expression. Values for the normalized difference range from 0 to 1.

For a group of N proteins in a complex, we generally compute the normalized difference not only for the pairs that are in direct physical contact, but for all (N2 − N)/2 theoretically possible pairs, thus arriving at a distribution of normalized differences of these pairs for each complex. We can then investigate this distribution of normalized differences and compare it with those among randomly chosen proteins. In our following discussion, we often refer to the median of the (N2 − N)/2 protein pairs as a key summarizing statistic.

In general, we assume stoichiometric ratios of 1:1 between subunits, although the above equation could be adjusted to account for other ratios. But even then, as shown in the Methods section below, we would not expect this quantity to always be close to zero because of the relationship between mRNA and protein abundance and also the noise in the expression data.

It should also be noted that there are obviously many limitations in treating GeneChip and SAGE data, our input (see Methods), as absolute measurements of mRNA expression (Schadt et al. 2000).

To judge the statistical significance of normalized differences for particular groups of proteins, we compare them to the control distribution of randomly chosen protein pairs (Fig. 1). An interesting theoretical aspect in this context is that if Ei and Ej are random variables with an exponential distribution (which is a close approximation to the actual distribution of expression of levels in the reference expression set), then Dij is distributed uniformly between 0 and 1 (Pitman 1993). This explains why we can observe a nearly uniform distribution of normalized differences for randomly selected pairs of proteins (Fig. 1).

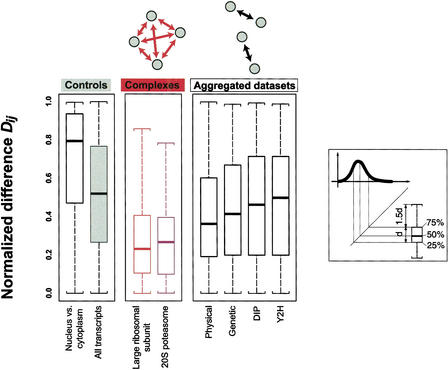
Figure 1.

Figure 1

Open in a new tab

Distributions of normalized differences for various groups of proteins in boxplot representation. The normalized difference Dij is a measure of the relative similarity of two absolute gene expression levels Ei and Ej. The middle panel shows the distribution for two protein complexes (the large ribosomal subunit and the 20S proteasome). Note that we considered all theoretically possible protein pairs within the protein complex (as indicated in the schematic drawing above the panel). The right panel shows the distribution for the aggregated data sets of protein-protein interactions (Y2H is yeast two-hybrid) (Bader and Hogue 2000; Cagney et al. 2000; Fellenberg et al. 2000; Ito et al. 2000; Schwikowski et al. 2000; Uetz et al. 2000; Uetz and Hughes 2000; Xenarios 2000; Ito et al. 2001). Unlike in the complexes, where we consider interactions among a whole group of proteins, the interactions in the aggregated data sets are specific to individual protein pairs (see schematic drawing). The left panel shows two control distributions of the normalized difference, on the left for pairs of nuclear and cytoplasmic proteins, which presumably, because of spatial separation, do not interact, and on the right for any random protein pair (“all transcripts”) in yeast. The distribution of nuclear versus cytoplasmic proteins is strongly skewed toward one (the maximum value of the normalized difference), which is partially explained by the fact that cytoplasmic proteins tend to have higher expression levels than cytoplasmic ones (Drawid 2000; Drawid and Gerstein 2000). The distribution of all transcripts is nearly uniform (with a median of 0.5) (see Methods). The complexes distributions are clearly skewed toward zero with medians between 0.2 and 0.3. The medians of the distributions of the aggregated data sets are still somewhat smaller than the control median, most notably for the physical interactions data set; on the other hand, there is virtually no difference between the control and the distribution of the yeast two-hybrid data set. The aggregated data, obviously, includes some interactions implied by the complexes, with the degree of intersection ranging from 35% for the physical interactions to ∼6% for Y2H.

Correlation of Expression Profiles for Relative Expression Levels

Analysis of expression profiles may be more useful than that of absolute levels for characterizing interacting proteins that exist in unequal but stoichiometrically related amounts (e.g., 3:1) as it refers to the relative shape of expression profiles. It can be carried out on data from cDNA microarrays (such as the Rosetta data) because only relative rather than absolute expression levels are necessary. Specifically, we look at the distribution of Pearson correlation coefficients for pairs of genes as the measure of similarity. Other measures of similarity are possible as well (D'haeseleer 1997; Wen et al. 1998; Heyer et al. 1999; Qian et al. 2001).

As the input for our procedure, we use the expression vectors or profiles of all the subunits of a complex and then compute their pair-wise correlations. Like for the normalized difference, we compute the correlation coefficients for all protein pairs in a complex, thus gaining a distribution of correlation coefficients. If the complex consists of N subunits, this yields (N2 − N)/2 different combinations of protein pairs and thus correlation coefficients. To summarize these distributions, we calculate the “average correlation” (meaning the average of all pair-wise correlations within a complex). As a suitable control to assess statistical significance, we use the distributions of correlation coefficients for random groups of proteins and their averages (see Methods). We would expect correlations of close to one for subunits in a tight complex. However, as we show in the Methods section, this will not be exactly the case because of the relationship between mRNA and protein abundances.

Specific Complexes

We first outline some results obtained for specific protein complexes, then we proceed to a more general overview of complexes.

Ribosome

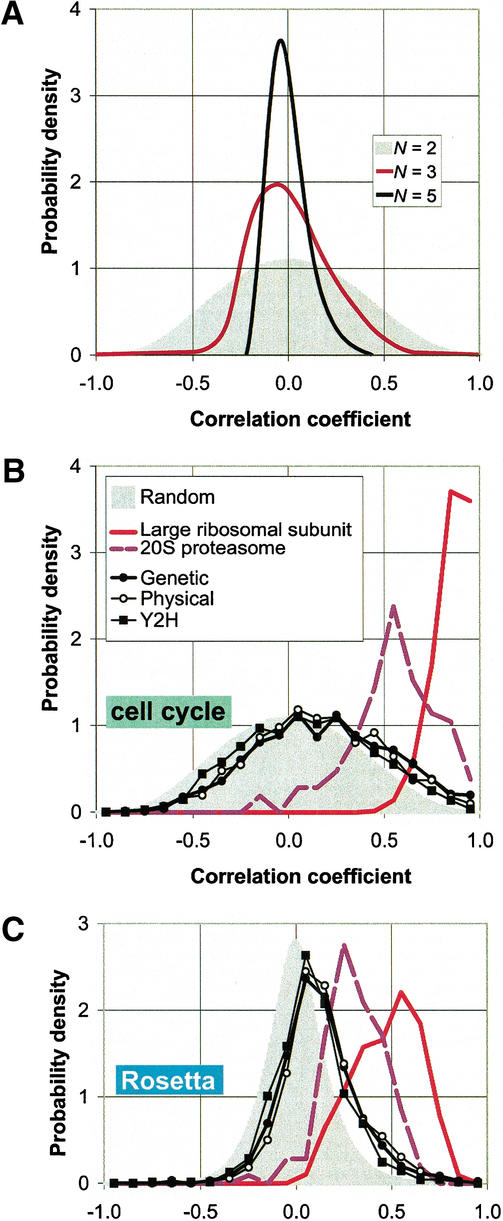
It has long been known that the mRNA expression levels of the ribosomal proteins are strongly correlated with one another (Johannes et al. 1999). Figure 1 shows the observed distribution of normalized differences for protein pairs in the large subunit of the cytoplasmic ribosome. The median of this distribution is 0.23, much lower than the median of 0.5 for randomly selected protein pairs. While there is a wide range of normalized differences (which may partially result from the fact that many proteins in the ribosome are known not to be expressed in a 1:1 ratio [Kruiswijk et al. 1978]), the ribosomal distribution is clearly skewed toward zero. Considering pairs of duplicated ORFs in the ribosome as one subunit by summing their expression levels leads to an even lower median normalized difference of 0.20 (data not shown). Distributions of the correlation coefficients for protein pairs within the large ribosomal subunit are shown in Figure 2. For both the cell cycle and the Rosetta data, the correlations tend to be much higher than the random control.

Figure 2.

Figure 2

Open in a new tab

Distributions of correlation coefficients between expression profiles. In A, we show distributions of the average correlation ρ̄N of N genes for the cell cycle experiments. The gray curve in the background represents the case N = 2 (i.e., simply the distribution of pair-wise correlations). In the case of N >2, ρ̄N is defined as the average of all possible (N2−N)/2 pairwise correlations among the N genes. We show here, as examples, the distributions for N = 3 and N  = 5. The distributions obviously become narrower, reflecting the fact that it becomes more unlikely to find large groups of strongly correlated genes at random as N increases. These distributions provide a suitable control for the observed correlations between pairs of genes (N  = 2) or for the average correlations among the subunits of a complex (N>2). We have developed a method to efficiently sample the distribution curves f(ρN) (see Methods). Based on the distribution function of f(ρN) we can calculate a one-sided P-value:

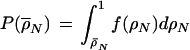graphic file with name M11.gif
This P-value then represents the chance that a group of N randomly selected genes could exhibit an average correlation greater than or equal to that of a complex with N proteins (see Fig. 3).

(B and C) The distribution of pair-wise correlations for both the cell cycle (Cho et al. 1998) and the Rosetta experiments (Hughes et al. 2000) in two protein complexes (the ribosome and the proteasome) as well as for the aggregated data sets (genetic, physical and yeast two-hybrid). The gray curves in the background are the control distributions for N  = 2 as explained above. The distributions for the ribosome and the proteasome are strongly shifted to the right of the control; this effect is much weaker for the data sets of aggregated interactions.

Similar observations can be made for the proteins in the small cytoplasmic ribosome. Key statistics are summarized in Figure 3 in comparison to those for other protein complexes. Furthermore, the two separate ribosome particles are strongly coregulated. In fact, the large and the small ribosomal particles cannot be differentiated by our measures of expression similarity.

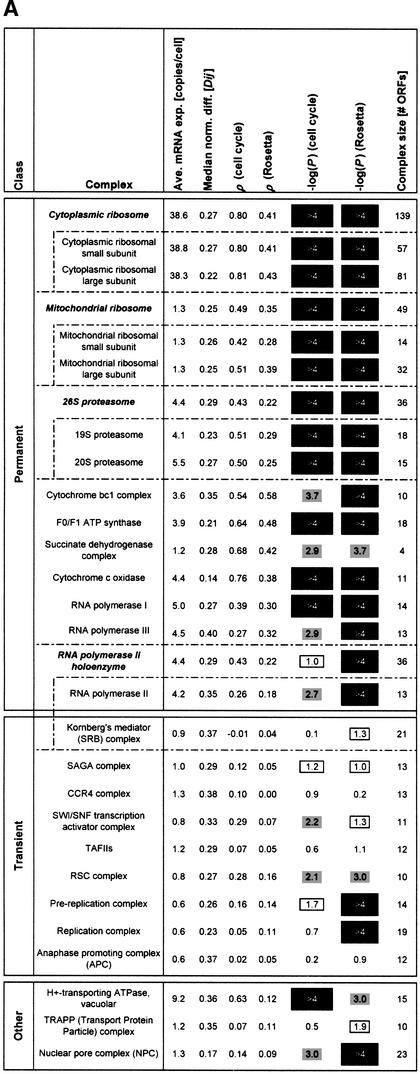
Figure 3.

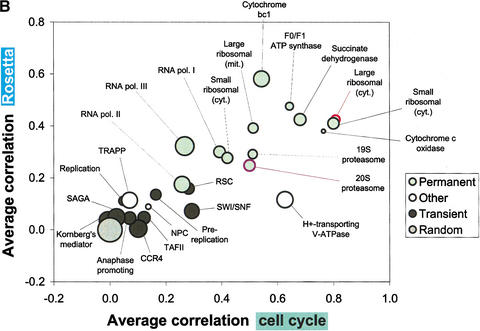
Figure 3

Figure 3

Open in a new tab

(A) Consolidates various key statistics shown in Figures 1 and 2 for the ribosome and proteasome as well as for a large number of protein complexes. We list all protein complexes from the MIPS catalog having at least 10 open reading frames (ORFs). The complexes are divided into three classes: permanent, transient, or other (see below). Some complexes can be divided into smaller subcomplexes (e.g., the ribosomes) as indicated. The table lists (from left to right) the average expression level of the complex, the median normalized difference (see Fig. 1A), the average correlation for the cell cycle and Rosetta experiments (see Fig. 2), the negative logarithm of the P-value of the average correlations in both experiments (see Fig. 2), and the size of the complex in terms of the number of ORFs. In general, the P-values for the average correlations are very low for most of the permanent protein complexes [accordingly, −log10(P) is very high], indicating that these averages are significantly greater than for random groups of proteins of the same size. The same cannot be observed for the transient protein complexes, for which the correlation averages are usually much smaller. The section “other” at the bottom of A contains complexes that are either difficult to classify as permanent/transient or for which, as a result of very small turnover rates, down-regulations of mRNA levels take a very long time to affect protein abundance. The H+-transporting ATPase can be thought of as containing a mixture of permanent and transient components at the same time (P. Kane, pers. comm.). The nuclear pore complex (NPC) and the TRAPP complex are known to have low turnover rates (Bucci and Wente 1997; Winey et al. 1997; Sacher et al. 1998; Barrowman et al. 2000). The NPC has relatively small average correlations, but this still yields P-values of 10–3 (cell cycle) and <10−4 (Rosetta) because the nuclear pore complex is a relatively large aggregation of proteins, and even these weak average correlations are very unlikely to occur for random groups of proteins of this size. The TRAPP protein complex, while existing throughout the cell cycle, has a low turnover rate and as such its mRNA expression data would not be sufficient for our analysis. The RNA polymerase holoenzyme is composed of both permanent and transient components. Note that the MIPS complexes catalog does not include the SWI/SNF chromatin-remodeling complex and a subset of basal transcription factors (Wilson et al. 1996) as part of the holoenzyme, thus we list them separately here. The list does not include those categories from the MIPS complexes catalog that do not really represent protein complexes per se, but rather aggregations of disparate proteins that are involved in similar types of complex interactions, such as the “actin-associated” and “tubulin-associated” protein groups. (B) Shows a graphical representation of part of the protein complex statistics from A. The abscissa and ordinate represent the average correlations in the cell cycle and the Rosetta data, while the bubble sizes are a function of the normalized differences (larger bubbles represent larger normalized differences). In general, the permanent complexes tend to be located in the upper right region of the plot, whereas transient complexes are closer to the random control in the lower left.

Proteasome

A second example of a complex whose individual subunits are strongly coregulated is the proteasome, which is involved in protein degradation and responsible for the rapid breakdown of ubiquitinated proteins. Like the ribosome, the 26S proteasome can be divided into two subparticles: the 20S and the 19S (or 19S/22S regulatory particle). The 20S particle is present as a dimer in the center of the complex structure and contains the catalytic core, whereas two 19S particles are attached to both ends of the 20S particle dimer (Coux et al. 1996; Wilkinson et al. 1999).

The distribution of the normalized differences for all possible protein pairs in the 20S proteasome is shown in Figure 1. Like the ribosome, it is clearly skewed toward zero, compared to the control, with a median of 0.29. Figure 2 shows the distribution of correlation coefficients, which is strongly shifted to the right of the control, though to a lesser extent than that for the ribosome. An investigation of the crystal structure of 20S particle (Whitby et al. 2000) did not reveal any relationship with the gene expression differences (e.g., proteins with slightly more random correlations tending to be more on the surface of the particle).

Similar results can be observed for the 19S particle of the proteasome (Fig. 3A). Also, in terms of both measures of coexpression (normalized differences and correlation of expression profiles), the 19S and the 20S particles of the proteasome form a single unit that is difficult to separate. Part of the reason for this may be that the common classification into 19S and 20S particles is based on the purification procedure for the proteasome (M. Hochstrasser, pers. comm.) and thus does not necessarily reflect functional or biochemical properties in a direct way.

One subunit, Doa4p, exhibits a very low average correlation (−0.02). Biochemical studies have previously shown that not all proteasomes have Doa4p bound and that the Doa4p-proteasome interaction is more likely to be transitory (Papa and Hochstrasser 1993; Papa et al. 1999).

RNA Polymerase II Holoenzyme

We have seen above that the ribosome and proteasome can be regarded as strongly associated and coregulated multiparticle complexes. However, in some cases a complex contains more loosely associated components. An example is the RNA polymerase II holoenzyme, which contains the core RNA polymerase II together with the more loosely associated SRB complex (Kornberg's mediator) and other smaller components (such as the SWIF/SNF complex and the TAFIIs).

It is known that, unlike the RNA polymerase II core enzyme, the SRB complex and the other holoenzyme components are only needed for the transcription of a fraction of genes (Holstege et al. 1998). In other words, the holoenzyme is an example of a complex of transitory nature with a permanent core. This permanent-and-transitory structure is clearly evident in the gene expression analysis. For the core enzyme, the average correlation in both the cell cycle and Rosetta data sets are significantly higher than for the random control (Fig. 3). However, for the SRB complex and a variety of other, smaller components (e.g., the TAFIIs) the average correlations are virtually indistinguishable from the random control.

Replication Complex

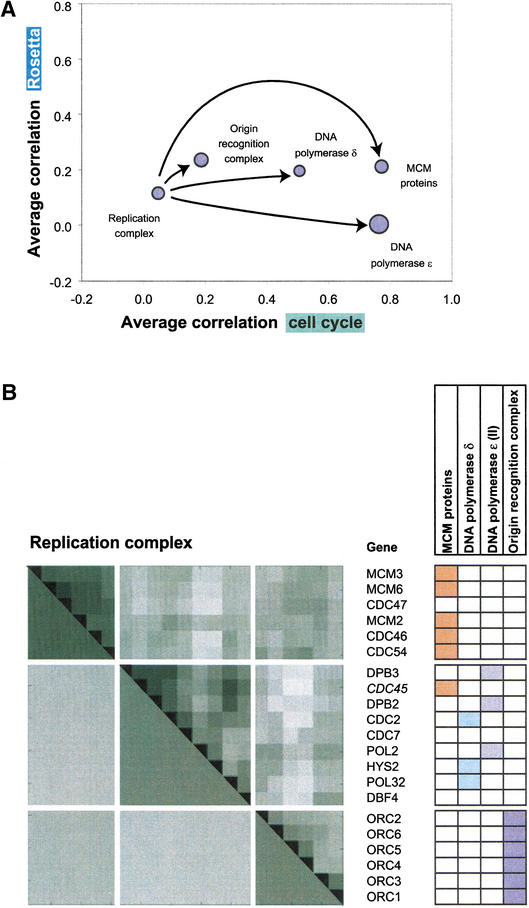
Another example of a transient complex is the replication complex, which binds to DNA and is needed for the initiation of replication. The replication complex can be subdivided into a number of subcomponents: the MCM proteins, the origin recognition complex, and the DNA polymerases δ and ɛ (Aparicio et al. 1997).

As a whole, the replication complex exhibits a low average correlation not significantly different from that of the random control (Fig. 3, 4). However, Figure 4 shows how the entire complex breaks into subcomponents in terms of correlations in the cell-cycle experiment. The individual correlations for each of the subcomponents are much higher than that of the complex as a whole. This indicates that the replication complex is composed of independent units in terms of expression regulation. Using the permanent-transient terminology, each subcomponent behaves similarly to an independent permanent complex, whereas the replication complex as a whole can be characterized as transient. The permanent subcomponents can be seen to come together to form a transient functional entity. (Note, this effect is more evident in the cell cycle experiment than the Rosetta data, as it should only be observable in a synchronized population of cells, not those averaged across the cell cycle.)

Figure 4.

Figure 4

Open in a new tab

(A) A representation of the replication complex and its components on the same coordinates as the protein complexes in Figure 3B. The transient replication complex can be decomposed into smaller complexes: the origin recognition complex, the MCM proteins, and the DNA polymerases δ and ɛ. Whereas the whole replication complex exhibits an average correlation close to zero (in both the cell cycle and the Rosetta data), the four smaller complexes show greater correlations in the cell cycle experiment. The four subcomplexes behave more like permanent complexes than the replication complex as a whole. (B) The correlation coefficient matrix for the subunits of the replication complex derived from the cell cycle data. The upper triangle of the correlation matrix shows the individual correlation coefficients for particular gene pairs (with darker colors indicating higher correlations). The lower triangle shows the average correlations for subgroups of proteins (representing the MCM proteins, the two DNA polymerases, and the origin of the replication complex) within the complex as a whole. The table on the right side shows which genes belong to which subgroups in different colors. The genes were ordered with unsupervised clustering (average linkage) without regard to their classification according to the three subgroups. It can be seen that this order reflects the separation according to the subgroups very well (only the proteins in the two DNA polymerase cannot be separated into two groups). An exception is the CDC45 protein that belongs to the MCM proteins but tends to cluster with the DNA polymerases.

Complexes in General: Permanent versus Transient

In discussing the specific examples above, we have found the permanent or transient nature of the association to be an important feature. This distinction is, in fact, valuable in a more general context. As shown in Figure 3, we have a priori formalized a division between “permanent” complexes, which are maintained throughout the cell cycle and most cellular conditions, and “transient” ones, which we define here as a group of proteins that do not consistently maintain their interactions. That is, the existence of a transient complex is temporal and specific to a part of the cell cycle or a subset of cellular states. We are aware that the division into the two absolute categories “permanent” and “transient” is perhaps somewhat oversimplifying as there can be varying degrees and combinations of these attributes (see Discussion).

In Figure 3, we show a general classification of the large MIPS complexes into permanent and transient classes, together with key statistics (details of the classification method are given in the legend). We list all complexes with more than 10 subunits (which together account for ∼80% of all the theoretically possible protein-protein interactions in the MIPS complexes), with smaller complexes listed on our website. Figure 3B shows a graphical representation of the complex list, synthesizing the correlations for both the Rosetta and cell-cycle experiments with the normalized differences. It clearly shows that there is a greater tendency for permanent complexes to have higher average correlations than for transient ones.

Comparing the average correlations in Figure 3A against random controls allows us to derive P-values for the statistical significance of the correlation. As shown in the figure, these are <10–4 for most of the permanent complexes. On the other hand, they are considerably higher, and thus less significant, for transient complexes. The separation between permanent and transient complexes is also evident in terms of the normalized difference statistics, although not as strongly.

Aggregated Protein-Protein Interaction Sets

From our analysis above, it seems reasonable to conclude that there is indeed a strong relationship between mRNA expression and the protein-protein interactions in “permanent” complexes. This raises the question whether or not similar observations can be made for other types of protein-protein interactions. We briefly summarize here the degree to which the interactions in the aggregated interaction data sets, such as the yeast two-hybrid data, are related to expression.

Figure 1 shows the distribution of normalized differences, and Figure 2 shows the distributions of correlation coefficients between interacting proteins in the aggregated data sets. The distributions of normalized differences are relatively similar to those of the transient protein complexes. The physical interactions show the smallest median normalized difference while the yeast two-hybrid interactions have a median normalized difference closest to the random control (∼0.5). Figure 2 shows that the correlation distributions for the aggregated data sets are fairly similar among themselves and only slightly shifted toward the right of the distribution curve for random protein pairs. This, again, is very similar to the behavior of transient protein complexes.

Thus, overall, it seems fair to conclude that the aggregated protein-protein interactions are related to mRNA expression in a similar fashion as the transient protein complexes.

DISCUSSION AND CONCLUSION

We have investigated the relationship of protein-protein interactions and mRNA expression levels, integrating and surveying a variety of data sources for yeast. We have focused our investigation on the protein interactions within specific complexes. While we have demonstrated a strong relationship between expression data and most permanent protein complexes, this relationship is much weaker for transient protein complexes as well as for the aggregated sets of protein-protein interactions (i.e., physical, genetic, and yeast two-hybrid interactions).

Issues with Permanent-Transient Classification

Our complex classification scheme—separating most complexes into either permanent or transient—while useful, cannot account for all complexes in the MIPS database. Some complexes may not clearly fit into the permanent-transient classification. We list a few of these as “other” in Figure 3. Moreover, the complexes list is a compilation of current biochemical knowledge and therefore reflects its inherent limitations (sometimes not all subunits are known or some proteins are mistakenly assigned to a complex).

Of course, even for the complexes that we do classify, the terms “transient” and “permanent” are somewhat of an over-simplification. In particular, our detailed discussions of the RNA polymerase II holoenzyme and the replication complex above are precisely two examples where our simplified terminology fails to completely explain the situation since these complexes are somewhere between fully “transient” and “permanent”.

One can think about the distinction between permanent and transient in terms of the mathematical model introduced in the Methods section. Whenever a complex is formed, its subunits tend to be expressed at equimolar protein concentrations: Pi≈Pj and dPi/dt≈dPj/dt (where Pi and Pj are the protein concentrations of two subunits i and j). If the complex is “permanent”, then these conditions should be approximately or vaguely met. If the complex is “transient”, then these conditions can be relaxed in those situations where the complex is not formed. There are some complexes that are always formed (“permanent”) whereas the “transient” complexes are only formed under particular conditions. There can be different degrees of being transient: for instance, complexes that are formed under 80% of conditions or those that are formed under 20% of conditions. The transient complex formed under 80% of conditions behaves almost like “permanent” (i.e., 100% of conditions), whereas the transient complex formed only 20% of the time would be expected to show less significant normalized differences and correlations.

If one goes as far as to accept the premise that the subunits in a complex should be present at equimolar amounts, then it is perhaps circular reasoning to say that they should also be coexpressed.

Complexes versus the Aggregated Interactions: The Need for Structures

We found it difficult to discern expression-based relationships in the aggregated data sets. This may be because of the generalized and heterogeneous nature of the aggregated data sets, (e.g., inconsistent physiological conditions, false positives, and false negatives). Moreover, both the aggregated sets and the transient complexes suffer partially from the limited amount of mRNA expression data as their interactions may occur under particular physiological conditions that may not be sampled by mRNA expression data. Our results, thus, illustrate the difficulty in drawing general conclusions for the pair-wise interaction sets and highlight the important role clearly resolved crystal structures of complexes, detailing protein interactions between subunits, have in studying protein-protein interactions.

Noise in the Expression and Interaction Data

In general, the interactions in the aggregated data sets exhibited surprisingly little deviation from randomness in terms of the coexpression of interaction pairs. This was most strongly observed for the yeast two-hybrid data. It is true that, overall, this deviation from randomness is statistically significant. All the same, the gene expression data and the aggregated protein interaction data do not reinforce each other strongly and it seems that the prediction of these type of interactions from expression data would be of little benefit.

Perhaps the most optimistic view of this situation is that the strong degree of independence of the two types of data makes both of them suitable for use in machine-learning approaches to characterize genes of unknown function: if they were strongly correlated, then one type of data could perhaps well replace the other since it represents very similar information. A negative view would be that the reason for the surprisingly weak relationship between the aggregated interactions and mRNA expression are to be found in the problems with the either the expression or the interaction data.

We feel confident that our results are robust to the noise in the expression data for the following reasons. With respect to the correlation analysis of expression profiles, roughly the same results (in terms of statistical significances) can be obtained for two independent data sets (the cell-cycle time course and the Rosetta knockout series). The normalized difference analysis is perhaps more sensitive to problems with the data, in particular, considering that the measurement of absolute expression levels with gene chips is problematic to start with. However, we have looked at an integrated data set from various chip experiments and the SAGE data, thus averaging out errors to some degree (see Methods). In addition, for both the correlation and the normalized difference analysis, we have concentrated on the statistical significance of distributions rather than relying on the error-prone data for individual protein pairs, thus observing more robust, aggregate trends for whole complexes and groups of proteins.

Part of the aggregated data, in particular the yeast two-hybrid data, represent a relatively new approach to studying protein-protein interactions and it is interesting to note that it, obviously, includes some interactions implied by the complexes. However, the degree of intersection with possible complexes interactions ranges from 35% for the physical interactions to only ∼6% for the yeast two-hybrid data (as a fraction of the number of interactions in the aggregated datasets). This is surprisingly low, given that the yeast two-hybrid data is from experiments that covered the complete genome (Uetz et al. 2000; Ito et al. 2001). Independently, Ito et al. (2001) reported that only a small fraction of the previous yeast two-hybrid data (Uetz et al. 2000) overlapped with their own yeast two-hybrid results. (Although Ito and colleagues assumed that their core data was similar in quality as the Uetz data, the fraction of interactions present in both data sets was only 16.8% for the Ito core and 20.4% for the Uetz data).

mRNA versus Protein Expression

The coregulation of subunits in a protein complex should be primarily observable in terms of protein abundance and only indirectly in terms of mRNA expression. Several recent studies have attempted to investigate the relationship between mRNA and protein expression levels in yeast cells and found them to be correlated to various degrees (Anderson and Seilhamer 1997; Futcher et al. 1999; Gygi et al. 1999; Greenbaum et al. 2001; Lian et al. 2001). Generally, post-transcriptional regulation is more difficult to investigate given the sparse data resources currently available for protein abundance levels. It is possible that in some situations coregulation occurs mostly on the protein level, almost independent of cellular mRNA levels. Particularly, those permanent complexes that do not have high levels of correlation in our analysis may be indicative of translational or post-translational control and could be a starting point for further experimental investigation. See Methods section for further discussion.

METHODS

Interactions Data Sources

The primary focus of this paper is the interactions occurring within specific complexes. These were obtained from the MIPS complexes catalog (Fellenberg et al. 2000), which represents a carefully annotated, comprehensive data set of protein complexes culled from the scientific literature. In addition, we looked at other types of protein-protein interactions from large “aggregated” data sets collecting many heterogeneous pair-wise interactions. We collected these from the MIPS catalogs of physical and genetic interactions (Fellenberg et al. 2000), databases of interacting proteins (DIP and BIND) (Bader and Hogue 2000; Xenarios 2000), and a comprehensive collection of yeast two-hybrid experiments (Cagney et al. 2000; Ito et al. 2000; Schwikowski et al. 2000; Uetz et al. 2000; Uetz and Hughes 2000; Ito et al. 2001). These interactions are subdivided into groups based on their method of discovery. They include physical interactions (e.g., collected through coimmunoprecipitation and copurification), genetic interactions (e.g., determined through genetic means such as synthetic lethality or suppression experiments), and yeast two-hybrid pairs.

Expression Data Sources

We included two different types of expression measurements in our analysis: absolute expression levels in vegetative yeast cells as determined by SAGE or gene chip experiments, and profiles of ratio-type expression data from microarray experiments. For the first type, we use a comprehensive reference set, which we merged and scaled together from a variety of Affymetrix GeneChip and SAGE data sets (Velculescu 1997; Holstege 1998; Roth et al. 1998; Jelinsky and Samson 1999) into a single representative data source (scaling details on our website; Greenbaum et al. 2001). For the expression profiles, we focused on two different data sets: a cell cycle experiment (Cho et al. 1998) and the Rosetta yeast compendium (Hughes et al. 2000). The two data sets provide a fairly good sampling of the possible cellular states of yeast and represent different experimental methodologies. The cell-cycle data contains expression profiles obtained from synchronized cells over the course of two cell cycles, whereas the Rosetta data contains genome-wide expression ratios for 300 stationary cell states, which are derived from 280 gene deletions and the 20 drug interaction experiments.

Efficient Calculation of the Average Correlations

For two expression ratio profiles Xi and Xj (transformed to average 0 and standard deviation 1), the Pearson correlation coefficient ρij is given by the dot product:

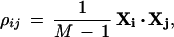graphic file with name M2.gif

where M is the number of elements in the profiles Xi and Xj. The profile X can be computed as a ‘Z-score’ from the measured expression ratio profile x, through the relation Xk = (xk − 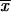Inline graphic)/σx, where 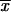Inline graphic denotes the average and σx the standard deviation of values in x, and Xk and xk are the kth components of their respective profiles.

Given a group of N genes, we can compute the correlation coefficient matrix R, where each element ρij of the matrix denotes the Pearson correlation coefficient between genes i and j. We can then compute the average correlation coefficient ρ̄ by averaging the matrix elements (excluding the main diagonal). This statistic gives an idea of the overall similarity of the expression profiles in a group of genes. Although there are O(N2) elements in R, the computation time for ρ̄ can be kept proportional to O(N) by using the linearity of the correlation to calculate ρ̄ as follows:

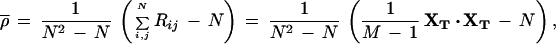graphic file with name M5.gif

where

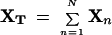graphic file with name M6.gif

is the sum of all expression profiles in the group of N genes.

Kinetic Model of the Relationship between Protein and mRNA Concentration

For a protein complex that is perfectly coregulated we can assume that its components are present at equimolar amounts and change similarly over time. So for the protein concentrations Pi and Pj of two different subunits i and j we would get: P1≈Pj and dPi/dt≈dPj/dt. Using a simple model for the relationship between mRNA and protein concentrations, we can see how even under these ideal conditions similarity measures based on the mRNA concentrations would deviate from perfect results. For instance, a linear kinetic model for the protein concentration Piand the mRNA concentration Ri of a subunit i in a complex is given by:

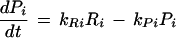graphic file with name M7.gif

where kRi is an mRNA translation rate constant and kPi is a protein degradation constant.

Why Expression Profile Correlations Have to Be Less Than One

For two subunits in a complex with Pi = Pj ≡ P and dPi/dt = dPj/dt, we can deduce:

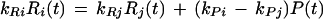graphic file with name M8.gif

It is clear that only under the strong assumption that the two protein degradation constants are equal (kPi = kPj)

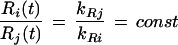graphic file with name M9.gif

from which would follow corr(Ri, Rj) = 1. Otherwise, corr(Ri,Rj) <1.

Why Normalized Differences Are Greater Than Zero

Furthermore, assuming steady-state (that is, dPi/dt = dPj/dt = 0), we can deduce the following relationship for the relationship between the mRNA levels of two complex subunits:

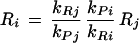graphic file with name M10.gif

Thus, the two mRNA expression levels are only expected to be equal if the ratios of the rate constants for translation and degradation are the same for both proteins. This is not necessarily the case for the subunits of a complex and therefore normalized differences should not be expected to be zero.

It is clear that the arguments above are based on a variety of simplifying assumptions. In reality, there are additional factors (such as the noise in the expression data, the stochastic nature of gene expression) that add even more difficulty to the analysis of mRNA levels.

Supplementary Information

Additional information can be found at genecensus.org/expression/interactions and bioinfo.mbb.yale.edu/expression/interactions.

The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.

Acknowledgments

MG acknowledges support by the Keck Foundation. RJ is supported by an IBM PhD Fellowship. The authors wish to thank Mark Hochstrasser and Jiang Qian for stimulating discussions.

Footnotes

E-MAIL Mark.Gerstein@Yale.edu ; FAX (360) 838-7861.

Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.205602.

REFERENCES

  1. Anderson L, Seilhamer J. A comparison of selected mRNA and protein abundances in human liver. Electrophoresis. 1997;18:533–537. doi: 10.1002/elps.1150180333. [DOI] [PubMed] [Google Scholar]
  2. Aparicio OM, Weinstein DM, Bell SP. Components and dynamics of DNA replication complexes in S. cerevisiae: Redistribution of MCM proteins and Cdc45p during S phase. Cell. 1997;91:59–69. doi: 10.1016/s0092-8674(01)80009-x. [DOI] [PubMed] [Google Scholar]
  3. Ashburner M, Ball CA, Blake JA, Botstein D, Butler H, Cherry JM, Davis AP, Dolinski K, Dwight SS, Eppig JT, et al. Gene ontology: Tool for the unification of biology. The Gene Ontology Consortium. Nat Genet. 2000;25:25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bader GD, Hogue CW. BIND—A data specification for storing and describing biomolecular interactions, molecular complexes and pathways. Bioinformatics. 2000;16:465–477. doi: 10.1093/bioinformatics/16.5.465. [DOI] [PubMed] [Google Scholar]
  5. Barrowman J, Sacher M, Ferro-Novick S. TRAPP stably associates with the Golgi and is required for vesicle docking. EMBO J. 2000;19:862–869. doi: 10.1093/emboj/19.5.862. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Brown MP, Grundy WN, Lin D, Cristianini N, Sugnet CW, Furey TS, Ares M, Jr, Haussler D. Knowledge-based analysis of microarray gene expression data by using support vector machines. Proc Natl Acad Sci. 2000;97:262–267. doi: 10.1073/pnas.97.1.262. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Bucci M, Wente SR. In vivo dynamics of nuclear pore complexes in yeast. J Cell Biol. 1997;136:1185–1199. doi: 10.1083/jcb.136.6.1185. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Cagney G, Uetz P, Fields S. High-throughput screening for protein-protein interactions using two-hybrid assay. Methods Enzymol. 2000;328:3–14. doi: 10.1016/s0076-6879(00)28386-9. [DOI] [PubMed] [Google Scholar]
  9. Califano A, Stolovitzky G, Tu Y. Analysis of gene expression microarrays for phenotype classification. Proc Int Conf Intell Syst Mol Biol. 2000;8:75–85. [PubMed] [Google Scholar]
  10. Cho RJ, Campbell MJ, Winzeler EA, Steinmetz L, Conway A, Wodicka L, Wolfsberg TG, Gabrielian AE, Landsman D, Lockhart DJ, et al. A genome-wide transcriptional analysis of the mitotic cell cycle. Mol Cell. 1998;2:65–73. doi: 10.1016/s1097-2765(00)80114-8. [DOI] [PubMed] [Google Scholar]
  11. Christendat D, Yee A, Dharamsi A, Kluger Y, Gerstein M, Arrowsmith CH, Edwards AM. Structural proteomics: Prospects for high throughput sample preparation. Prog Biophys Mol Biol. 2000a;73:339–345. doi: 10.1016/s0079-6107(00)00010-9. [DOI] [PubMed] [Google Scholar]
  12. Christendat D, Yee A, Dharamsi A, Kluger Y, Savchenko A, Cort JR, Booth V, Mackereth CD, Saridakis V, Ekiel I, et al. Structural proteomics of an archaeon. Nat Struct Biol. 2000b;7:903–909. doi: 10.1038/82823. [DOI] [PubMed] [Google Scholar]
  13. Coux O, Tanaka K, Goldberg AL. Structure and functions of the 20S and 26S proteasomes. Annu Rev Biochem. 1996;65:801–847. doi: 10.1146/annurev.bi.65.070196.004101. [DOI] [PubMed] [Google Scholar]
  14. D'haeseleer P, Wen X, Fuhrman S, Somogyi R. Mining the gene expression matrix: Inferring gene relationships from large scale gene expression data. In: Holcombe PM, editor. Information processing in cells and tissues. New York: Plenum; 1997. pp. 203–212. [Google Scholar]
  15. Drawid A, Jansen R, Gerstein M. Genome-wide analysis relating expression level with protein subcellular localization. Trends Genet. 2000;16:426–430. doi: 10.1016/s0168-9525(00)02108-9. [DOI] [PubMed] [Google Scholar]
  16. Drawid A, Gerstein M. A Bayesian system integrating expression data with sequence patterns for localizing proteins: Comprehensive application to the yeast genome. J Mol Biol. 2000;301:1059–1075. doi: 10.1006/jmbi.2000.3968. [DOI] [PubMed] [Google Scholar]
  17. Eisenberg D, Marcotte EM, Xenarios I, Yeates TO. Protein function in the post-genomic era. Nature. 2000;405:823–826. doi: 10.1038/35015694. [DOI] [PubMed] [Google Scholar]
  18. Emili AQ, Cagney G. Large-scale functional analysis using peptide or protein arrays. Nat Biotechnol. 2000;18:393–397. doi: 10.1038/74442. [DOI] [PubMed] [Google Scholar]
  19. Fellenberg M, Albermann K, Zollner A, Mewes HW, Hani J. Integrative analysis of protein interaction data. Proc Int Conf Intell Syst Mol Biol. 2000;8:152–161. [PubMed] [Google Scholar]
  20. Futcher B, Latter GI, Monardo P, McLaughlin CS, Garrels JI. A sampling of the yeast proteome. Mol Cell Biol. 1999;19:7357–7368. doi: 10.1128/mcb.19.11.7357. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Gaasterland T, Bekiranov S. Making the most of microarray data. Nat Genet. 2000;24:204–206. doi: 10.1038/73392. [DOI] [PubMed] [Google Scholar]
  22. Gerstein M, Jansen R. The current excitement in bioinformatics-analysis of whole-genome expression data: How does it relate to protein structure and function? Curr Opin Struct Biol. 2000;10:574–584. doi: 10.1016/s0959-440x(00)00134-2. [DOI] [PubMed] [Google Scholar]
  23. Greenbaum, D., Jansen, R., and Gerstein, M. 2002. Analysis of mRNA expression and protein abundance data: An approach for the comparison of the enrichment of features in the cellular population of proteins and transcripts. Bioinformatics. (in press). [DOI] [PubMed]
  24. Golub TR, Slonim DK, Tamayo P, Huard C, Gaasenbeek M, Mesirov JP, Coller H, Loh ML, Downing JR, Caligiuri MA, et al. Molecular classification of cancer: Class discovery and class prediction by gene expression monitoring. Science. 1999;286:531–537. doi: 10.1126/science.286.5439.531. [DOI] [PubMed] [Google Scholar]
  25. Gygi SP, Rochon Y, Franza BR, Aebersold R. Correlation between protein and mRNA abundance in yeast. Mol Cell Biol. 1999;19:1720–1730. doi: 10.1128/mcb.19.3.1720. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Heyer LJ, Kruglyak S, Yooseph S. Exploring expression data: Identification and analysis of coexpressed genes. Genome Res. 1999;9:1106–1115. doi: 10.1101/gr.9.11.1106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Hishigaki H, Nakai K, Ono T, Tanigami A, Takagi T. Assessment of prediction accuracy of protein function from protein-protein interaction data. Yeast. 2001;18:523–531. doi: 10.1002/yea.706. [DOI] [PubMed] [Google Scholar]
  28. Holstege FC, Jennings EG, Wyrick JJ, Lee TI, Hengartner CJ, Green MR, Golub TR, Lander ES, Young RA. Dissecting the regulatory circuitry of a eukaryotic genome. Cell. 1998;95:717–728. doi: 10.1016/s0092-8674(00)81641-4. [DOI] [PubMed] [Google Scholar]
  29. Hughes TR, Marton MJ, Jones AR, Roberts CJ, Stoughton R, Armour CD, Bennett HA, Coffey E, Dai H, He YD, et al. Functional discovery via a compendium of expression profiles. Cell. 2000;102:109–126. doi: 10.1016/s0092-8674(00)00015-5. [DOI] [PubMed] [Google Scholar]
  30. Ito T, Chiba T, Ozawa R, Yoshida M, Hattori M, Sakaki Y. A comprehensive two-hybrid analysis to explore the yeast protein interactome. Proc Natl Acad Sci. 2001;98:4569–4574. doi: 10.1073/pnas.061034498. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Ito T, Tashiro K, Muta S, Ozawa R, Chiba T, Nishizawa M, Yamamoto K, Kuhara S, Sakaki Y. Toward a protein-protein interaction map of the budding yeast: A comprehensive system to examine two-hybrid interactions in all possible combinations between the yeast proteins. Proc Natl Acad Sci. 2000;97:1143–1147. doi: 10.1073/pnas.97.3.1143. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Jansen R, Gerstein M. Analysis of the yeast transcriptome with structural and functional categories: Characterizing highly expressed proteins. Nucleic Acids Res. 2000;28:1481–1488. doi: 10.1093/nar/28.6.1481. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Jelinsky SA, Samson LD. Global response of Saccharomyces cerevisiae to an alkylating agent. Proc Natl Acad Sci. 1999;96:1486–1491. doi: 10.1073/pnas.96.4.1486. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Johannes G, Carter MS, Eisen MB, Brown PO, Sarnow P. Identification of eukaryotic mRNAs that are translated at reduced cap binding complex eIF4F concentrations using a cDNA microarray. Proc Natl Acad Sci. 1999;96:13118–13123. doi: 10.1073/pnas.96.23.13118. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Kruiswijk T, Planta RJ, Mager WH. Quantitative analysis of the protein composition of yeast ribosomes. Eur J Biochem. 1978;83:245–252. doi: 10.1111/j.1432-1033.1978.tb12089.x. [DOI] [PubMed] [Google Scholar]
  36. Li B, Nierras CR, Warner JR. Mol Cell Biol. 1999;19:5393–5404. doi: 10.1128/mcb.19.8.5393. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Lian Z, Wang L, Yamaga S, Bonds W, Beazer-Barclay Y, Kluger Y, Gerstein M, Newburger PE, Berliner N, Weissman SM. Genomic and proteomic analysis of the myeloid differentiation program. Blood. 2001;98:513–524. doi: 10.1182/blood.v98.3.513. [DOI] [PubMed] [Google Scholar]
  38. Luscombe NM, Laskowski RA, Westhead DR, Milburn D, Jones S, Karmirantzou M, Thornton JM. New tools and resources for analysing protein structures and their interactions. Acta Crystallogr D Biol Crystallogr. 1998;54:1132–1138. doi: 10.1107/s0907444998007318. [DOI] [PubMed] [Google Scholar]
  39. Mewes HW, Frishman D, Gruber C, Geier B, Haase D, Kaps A, Lemcke K, Mannhaupt G, Pfeiffer F, Schuller C, Stocker S, Weil B. MIPS: A database for genomes and protein sequences. Nucleic Acids Res. 2000;28:37–40. doi: 10.1093/nar/28.1.37. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Nomura M. Regulation of ribosome biosynthesis in Escherichia coli and Saccharomyces cerevisiae: Diversity and common principles. J Bacteriol. 1999;181:6857–6864. doi: 10.1128/jb.181.22.6857-6864.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Papa FR, Amerik AY, Hochstrasser M. Interaction of the Doa4 deubiquitinating enzyme with the yeast 26S proteasome. Mol Biol Cell. 1999;10:741–756. doi: 10.1091/mbc.10.3.741. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Papa FR, Hochstrasser M. The yeast DOA4 gene encodes a deubiquitinating enzyme related to a product of the human tre-2 oncogene. Nature. 1993;366:313–319. doi: 10.1038/366313a0. [DOI] [PubMed] [Google Scholar]
  43. Pitman J. Probability. New York: Springer-Verlag; 1993. [Google Scholar]
  44. Planta RJ. Regulation of ribosome synthesis in yeast. 1997. Yeast. 1997;13:1505–1518. doi: 10.1002/(SICI)1097-0061(199712)13:16<1505::AID-YEA229>3.0.CO;2-I. [DOI] [PubMed] [Google Scholar]
  45. Qian, J., Dolled-Filhart, M., Lin, J., and Gerstein, M. 2002. Beyond synexpression relationships: Clustering of time shifted and inverted gene expression profiles identifies new biologically relevant interactions. J. Mol. Biol. (in press). [DOI] [PubMed]
  46. Raychaudhuri S, Sutphin PD, Chang JT, Altman RB. Basic microarray analysis: Grouping and feature reduction. Trends Biotechnol. 2001;19:189–193. doi: 10.1016/s0167-7799(01)01599-2. [DOI] [PubMed] [Google Scholar]
  47. Roth FP, Hughes JD, Estep PW, Church GM. Finding DNA regulatory motifs within unaligned noncoding sequences clustered by whole-genome mRNA quantitation. Nat Biotechnol. 1998;16:939–945. doi: 10.1038/nbt1098-939. [DOI] [PubMed] [Google Scholar]
  48. Sacher M, Jiang Y, Barrowman J, Scarpa A, Burston J, Zhang L, Schieltz D, Yates JR, 3rd, Abeliovich H, Ferro-Novick S. TRAPP, a highly conserved novel complex on the cis-Golgi that mediates vesicle docking and fusion. EMBO J. 1998;17:2494–2503. doi: 10.1093/emboj/17.9.2494. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Schadt EE, Li C, Su C, Wong WH. Analyzing high-density oligonucleotide gene expression array data. J Cell Biochem. 2000;80:192–202. [PubMed] [Google Scholar]
  50. Schwikowski B, Uetz P, Fields S. A network of protein-protein interactions in yeast. Nat Biotechnol. 2000;18:1257–1261. doi: 10.1038/82360. [DOI] [PubMed] [Google Scholar]
  51. Subrahmanyam YV, Yamaga S, Prashar Y, Lee HH, Hoe NP, Kluger Y, Gerstein M, Goguen JD, Newburger PE, Weissman SM. RNA expression patterns change dramatically in human neutrophils exposed to bacteria. Blood. 2001;97:2457–2468. doi: 10.1182/blood.v97.8.2457. [DOI] [PubMed] [Google Scholar]
  52. Teichmann SA, Murzin AG, Chothia C. Determination of protein function, evolution and interactions by structural genomics. Curr Opin Struct Biol. 2001;11:354–363. doi: 10.1016/s0959-440x(00)00215-3. [DOI] [PubMed] [Google Scholar]
  53. Uetz P, Giot L, Cagney G, Mansfield TA, Judson RS, Knight JR, Lockshon D, Narayan V, Srinivasan M, Pochart P, et al. A comprehensive analysis of protein-protein interactions in Saccharomyces cerevisiae. Nature. 2000;403:623–627. doi: 10.1038/35001009. [DOI] [PubMed] [Google Scholar]
  54. Uetz P, Hughes RE. Systematic and large-scale two-hybrid screens. Curr Opin Microbiol. 2000;3:303–308. doi: 10.1016/s1369-5274(00)00094-1. [DOI] [PubMed] [Google Scholar]
  55. Velculescu VE, Zhang L, Zhou W, Vogelstein J, Basrai MA, Bassett DE, Jr, Hieter P, Vogelstein B, Kinzler KW. Characterization of the yeast transcriptome. Cell. 1997;88:243–251. doi: 10.1016/s0092-8674(00)81845-0. [DOI] [PubMed] [Google Scholar]
  56. Walhout AJ, Vidal M. High-throughput yeast two-hybrid assays for large-scale protein interaction mapping. Methods. 2001;24:297–306. doi: 10.1006/meth.2001.1190. [DOI] [PubMed] [Google Scholar]
  57. Wen X, Fuhrman S, Michaels GS, Carr DB, Smith S, Barker JL, Somogyi R. Large-scale temporal gene expression mapping of central nervous system development. Proc Natl Acad Sci. 1998;95:334–339. doi: 10.1073/pnas.95.1.334. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Westhead DR, Slidel TW, Flores TP, Thornton JM. Protein structural topology: Automated analysis and diagrammatic representation. Protein Sci. 1999;8:897–904. doi: 10.1110/ps.8.4.897. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Whitby FG, Masters EI, Kramer L, Knowlton JR, Yao Y, Wang CC, Hill CP. Structural basis for the activation of 20S proteasomes by 11S regulators. Nature. 2000;408:115–120. doi: 10.1038/35040607. [DOI] [PubMed] [Google Scholar]
  60. Wilkinson CR, Penney M, McGurk G, Wallace M, Gordon C. The 26S proteasome of the fission yeast Schizosaccharomyces pombe. Philos Trans R Soc Lond B Biol Sci. 1999;354:1523–1532. doi: 10.1098/rstb.1999.0496. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Wilson CJ, Chao DM, Imbalzano AN, Schnitzler GR, Kingston RE, Young RA. RNA polymerase II holoenzyme contains SWI/SNF regulators involved in chromatin remodeling. Cell. 1996;84:235–244. doi: 10.1016/s0092-8674(00)80978-2. [DOI] [PubMed] [Google Scholar]
  62. Winey M, Yarar D, Giddings TH, Jr, Mastronarde DN. Nuclear pore complex number and distribution throughout the Saccharomyces cerevisiae cell cycle by three-dimensional reconstruction from electron micrographs of nuclear envelopes. Mol Biol Cell. 1997;8:2119–2132. doi: 10.1091/mbc.8.11.2119. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Woolford JL, Warner JR. In. In: Broach JR, Pringle JR, Jones EW, editors. The molecular and cellular biology of the yeast Saccharomyces: Genome dynamics, protein synthesis, and energetics. Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press; 1991. pp. 587–626. [Google Scholar]
  64. Xenarios I, Rice DW, Salwinski L, Baron MK, Marcotte EM, Eisenberg D. DIP: The database of interacting proteins. Nucleic Acids Res. 2000;28:289–291. doi: 10.1093/nar/28.1.289. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES