Gene Expression Analysis with Universal n-mer Arrays

Abstract

Gene expression profiling is one of the many applications that have benefited from the massively parallel nucleic acid detection capability of DNA microarrays. Current expression arrays, however, are expensive and inflexible. They are custom-designed for each organism and they do not offer the possibility of incorporating updated genomic information without production of a new chip. One possible solution is the development of a universal chip, consisting of all 4ⁿ possible DNA sequences of length n. Studying different organisms or new genes would simply require modifications to the hybridization pattern analysis software. The key problem is to find a value of n that is large enough to afford sufficient specificity, yet is small enough for practical fabrication and readout. We developed an analytical model, supported by computer-assisted calculation with yeast and mouse transcript data, to argue that it is both practical and useful to fabricate n-mer arrays with 10 ⩽ n ⩽ 16.

The ability of DNA microarrays to measure thousands of binding interactions simultaneously has led to their rapid adoption in many applications: gene expression profiling (Marton et al. 1998; Spellman et al. 1998), DNA sequencing (Drmanac et al. 1998), genomic fingerprinting (Landegren et al. 1998), and studies of DNA-binding proteins (Bulyk et al. 1999). Diverse methods for fabricating arrays have been developed in the past several years, some based on the deposition of cDNA libraries and/or oligonucleotides by robots (Schena et al. 1995) or ink-jet printers (Okamoto et al. 2000) and others based on in situ DNA synthesis using photolithographic (Lockhart et al. 1996) or ink-jet technology (Hughes et al. 2001).

A drawback of all of these methods is that one must carefully choose, in advance, which sequences to probe. As a result, revisions to the arrays to correct mistakes or incorporate new genomic information are costly, requiring arrays to be redesigned and manufactured. It is desirable to have a universal gene expression chip that is applicable to all organisms, from bacteria to human, including those that lack complete cDNA libraries or whose genomes are not yet sequenced.

One way to obtain universality is to synthesize a combinatorial n-mer array containing all 4ⁿ possible oligos of length n, the key problem being to find a value of n that is large enough to afford sufficient specificity, yet is small enough for practical fabrication and readout. Combinatoric n-mer arrays can be fabricated in a small number of simple steps using conventional solid phase synthesis chemistry and arrays of parallel fluid channels in perpendicular orientations to mask the reagents (Southern and Maskos 1994).

Until high-resolution non-optical readout methods become practical, microarray densities will be constrained by the optical diffraction limit. With this lower bound of ∼0.28 μm on pixel size, n-mer arrays are limited to 8×10⁹ distinct spots per square inch, corresponding roughly to a 16-mer array on a 1" × 1" chip. Although it is possible to fabricate arrays with larger areas we consider here arrays whose size (one inch square) is comparable to the current state of the art to facilitate sensitivity comparisons. Therefore, we address the question of whether one can extract useful gene expression information from combinatorial arrays of short (i.e., n ⩽ 16) oligonucleotides.

We first develop an analytical model to predict, for a given value of n and a particular genome, the average ambiguity of the resulting hybridization pattern. With the model, we argue that for a certain minimum value of n, the ambiguity is sufficiently low that individual gene expression levels can be extracted from the hybridization data.

RESULTS AND DISCUSSION

Basic Analytical Model

Hybridization of a single labeled mRNA species to an n-mer array will cause numerous spots to fluoresce, yielding a characteristic “fingerprint” pattern. A diverse sample of mRNA transcripts yields an equilibrium hybridization pattern which is a linear superposition of numerous overlapping fingerprints, a pattern from which gene expression levels can be deduced by inverting a huge matrix of size 4ⁿ, the number of distinct sequences on the array (see Methods). This calculation is impractically large, but can be avoided by taking advantage of the vast redundancy inherent in a combinatorial array. One can ignore the ambiguous oligonucleotides that bind many different transcripts, instead concentrating on the information-rich oligonucleotides that bind few transcripts. We formalize this approach by defining the “degeneracy” of an n-mer as the number of different mRNA transcripts it can capture, which of course depends on the transcriptome being analyzed. In the best case, one could find an oligonucleotide that binds each transcript uniquely; however, it is more realistic to expect to find small oligonucleotide groups, each oligo of which binds only to transcripts in a small independent group. In these cases, the aforementioned matrix has vastly reduced dimension, is sparse, and is in block-diagonal form, greatly simplifying its inversion. The lower the average degeneracy, the easier is the construction of the block-diagonal matrix.

We now describe an analytic model that predicts the average degeneracy of the N_o = 4ⁿ distinct oligonucleotides on an n-mer array when analyzing a transcriptome of N_g “genes”. An individual mRNA transcript of length ℓ has b = ℓ + 1 − n ≈ ℓ subsequences of length n, any of which can serve as a site for binding the complementary n-mer affixed to the array. Assuming the transcript has a random nucleotide sequence, the probability that a particular n-mer captures the transcript is p = b/N_o. This is a simple Bernoulli trial; to compute the expected number of different transcripts to which the n-mer binds (i.e., its degeneracy d), it is necessary to carry out N_g Bernoulli trials, one for each transcript. The result is a binomial distribution of degeneracies that can be approximated by a Poisson distribution P₀(d;λ)=e^−λλ^d/d!, in which λ = N_gp is the average degeneracy. One can account for non-uniform transcript length by computing the degeneracy distribution as a weighted average of Poisson distributions:

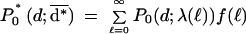1

in which ƒ(ℓ) is the fraction of transcripts with length ℓ. The mean value of this new distribution is:

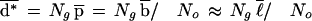2

where ℓ is the average transcript length.

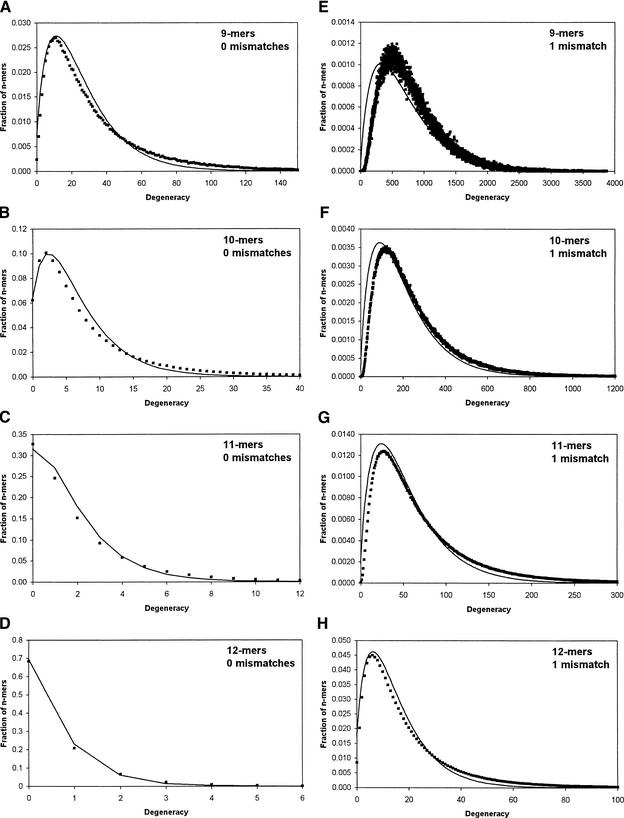
The predictions of this model are compared with the true degeneracies calculated from yeast ORFs and mouse transcripts in Table 1 and Figure 1. It is well known that there are significant statistical biases in nucleotide and codon distributions (Nakamura et al. 2000). Although this model neglects these variations, its predictions agree surprisingly well with the genomic data. The slightly reduced agreement for larger average degeneracy values can be attributed primarily to a clipping effect that occurs when the average degeneracy value is close to its maximum possible value (i.e., the number of genes), a regime in which we are not interested.

Table 1.

Comparison of Average Degeneracy Values Predicted by the Analytical Model with Those Calculated from Actual Yeast and Mouse Genomic Sequence Data

Organism	n	0 Mismatches		1 Mismatch
d (Actual)	d (Predicted)	d (Actual)	d (Predicted)
yeast	7	479.3	544.2	4190	11970
yeast	8	130.2	135.9	2120	3399
yeast	9	33.42	33.96	790.0	950.9
yeast	10	8.420	8.485	245.8	263.0
yeast	11	2.110	2.120	70.29	72.07
yeast	12	0.5275	0.5295	19.39	19.59
mouse	9	130.2	134.1	3308	3754
mouse	10	32.66	33.44	976.2	1037
mouse	11	8.161	8.343	273.8	283.6
mouse	12	2.037	2.081	74.96	77.00
mouse	13	0.518	0.519	20.27	20.77
mouse	14	0.127	0.130	5.442	5.569

Figure 1.

Comparison of degeneracy histograms determined from actual yeast genomic sequences (square markers) with predictions of the analytical model (continuous line). Each histogram shows the fraction of n-mers having a given degeneracy value. Predicted curves were obtained by taking a weighted average of Poisson distributions as in Equation 1, with the weights corresponding to the distribution of transcript lengths in yeast. There are no fitted parameters. Actual histograms were generated with custom computer software that counted the degeneracy of each n-mer in the yeast genome. (A–D) Histograms for the case of 0 mismatches for n = 9, n = 10, n = 11, and n = 12, respectively. (E–H) Histograms for the case of 1 mismatch for the same range of n-values.

Accounting for Mismatches

In practice, hybridization is imperfect and stable duplexes can form between strands that are not perfect complements. As a first approximation, we suppose that the hybridization stringency can be tailored to prevent duplex formation when the number of mismatched positions exceeds some threshold m. Implementing this assumption requires one to establish hybridization and wash conditions that provide adequate stringency for all spots on the array simultaneously.

Comparing the melting curve for a perfectly matched duplex with that of a mismatched duplex indicates that a window of hybridization temperatures exists within which the perfect match is stable and the mismatch sufficiently unstable that the two can be distinguished. Fortunately, the width of this temperature window is largest for short oligonucleotides because single-nucleotide mismatches have an increasingly destabilizing effect as oligo length is reduced. Numerous experiments have shown that single-nucleotide mismatches can be distinguished reliably from perfect matches. This capability is exemplified by Wang et al. (1998), who designed several huge microarrays (with 150,000–300,000 features) to detect single nucleotide polymorphisms (SNPs) in the human genome. They were able resolve single-nucleotide central mismatches for all features on each chip simultaneously. The discrimination of end mismatches is somewhat more difficult because of the narrower range of suitable temperatures, but successful techniques have been shown by several groups. Kutyavin et al. (2000) used minor-groove-binding molecules that stabilize properly formed double helices. Yershov et al. (1996), Stomakhin et al. (2000), and Maldonado-Rodriquez et al. (1999) described methods whereby duplexes with properly matched ends are stabilized by the phenomenon of contiguous base stacking. It has also been reported that this level of discrimination can be achieved by hybridizing DNA to a PNA (peptide nucleic acid) array, because of the higher mismatch sensitivity of DNA–PNA binding compared to DNA–DNA binding (Weiler et al. 1997; Igloi 1998; Ratilainen et al. 2000).

To achieve adequate discrimination across the whole n-mer array simultaneously requires a means of reducing the intrinsic variation in melting temperatures (owing to the variation in CG content from 0%–100%, among other factors). This is an active area of research and already a number of groups have shown successful techniques with small arrays. For example, Sonowski et al. (1997) reported single-nucleotide mismatch discrimination under the same hybridization and wash conditions for two different sequences differing in intrinsic melting temperature by 20°C. More recently, chips with several thousand addressable spots have been produced based on this electronic stringency control method (Heller et al. 2000). Other approaches include the addition of auxiliary molecules during hybridization (Rees et al. 1993; Jacobs et al. 1988), the use of modified bases, or the modification of the DNA backbone to homogenize melting temperatures (Hoheisel 1996). Although progress in array technology may yield nearly perfect hybridizations, for practical purposes we have relaxed this requirement in the conclusions that follow. Therefore, we assume that sequences can bind with up to one mismatch.

Mismatches increase the probability p that a gene binds to a particular immobilized n-mer. The increase is a simple multiplicative factor,

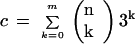3

reflecting the increased number of subsequences that are sufficiently complementary (i.e., having ⩽m mismatches) for binding to the n-mer. An alternative viewpoint is that the number of distinct oligonucleotides on the array is reduced by this factor to N = 4ⁿ/c. Furthermore, because the decreased number of spots corresponds to a lower effective value for the n-mer length, n* = log₄(4ⁿ/c) = n−log₄(c), one can quantify the effect of mismatches. When the analytic model is modified to include the effects of mismatches, we continue to find excellent agreement between predictions and actual calculation (Table 1).

Truncation of Transcripts

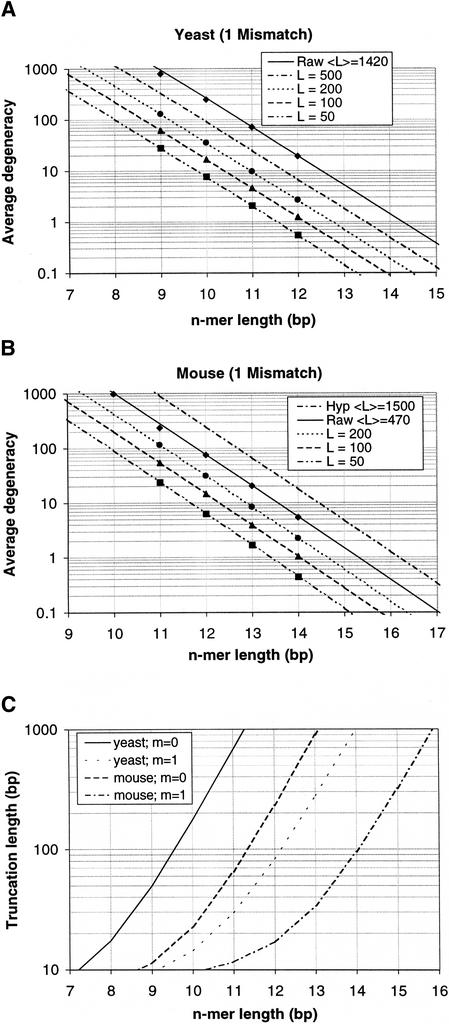
The size of the n-mer array is not the sole degree of freedom available to reduce the average degeneracy; one can also reduce ℓ, the average transcript length. With appropriate nucleases and controlled reaction conditions it should be possible to truncate the length of all transcripts before hybridization according to one of two methods, (1) reduction in transcript length by an average length ΔL from one end or (2) reduction of all transcripts to the same average length L. For example, the first method could be implemented by tailoring the duration of enzymatic digestion to remove a desired average number of nucleotides from all transcripts. To implement the second method, one could protect the transcripts along a desired length (e.g., by polymerizing a second strand for a controlled time), subsequently digesting away the remaining unprotected portion. Because truncation would occur before hybridization, it can be incorporated into the analytic model simply by replacing ℓ everywhere with ℓ–ΔL or with L, depending on the truncation scheme. Figures 2A,B show that the model continues to yield accurate predictions with truncated transcripts in addition to mismatches.

Figure 2.

Predictions of average degeneracy compared with calculations from actual sequence data for the case of 1 mismatch for yeast (A) and mouse (B). Continuous lines represent predictions (with no fitted parameters) of average degeneracy as a function of the n-mer length n for varying degrees of transcript length truncation to a fixed length L, computed from Equation 2 with modifications for mismatches and length truncation. (Raw designates the untruncated cases). Discrete points represent the actual average degeneracy values. Owing to the presence of many ESTs in the mouse UniGene database, the average transcript length for mouse is reported as much lower than yeast, so we have included a predicted curve for a hypothetical average gene length of 1500 bp. (C) Predicted relationship between parameter values to achieve an average degeneracy of 1 (the trivial case).

Estimating n

Having validated the model over a wide range of parameter values, we can estimate useful sizes for n-mer arrays. Figure 2C illustrates combinations of parameter values that are predicted to yield an average degeneracy of 1 — the “ideal” case, for which gene expression levels can be solved trivially. As shown for the case of one mismatch, achieving this target in yeast requires a 14-mer array if transcripts are untruncated or a 12-mer array after transcript truncation to ∼80 bp. In mouse, the target degeneracy is nearly realized with a 15-mer array without truncation or a 14-mer array after truncation to ∼90 bp.

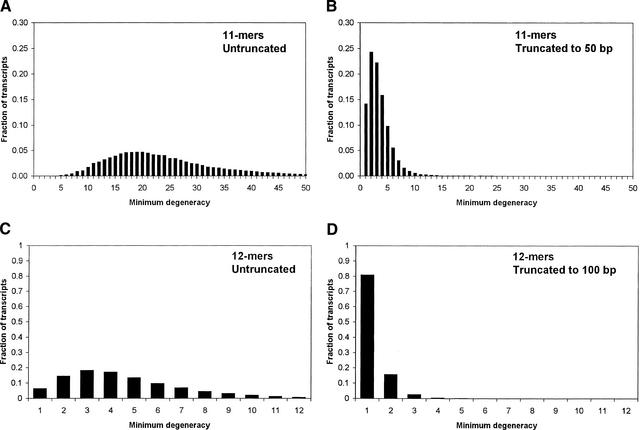
Our results so far have considered the average degeneracy of all n-mers on the array. However, when the degeneracy is sufficiently low, only a tiny subset of the oligos is needed for monitoring individual gene expression levels. A logical starting point is considering, for each gene, the minimum degeneracy n-mer to which it can bind. Transcripts having minimum degeneracy equal to 1 are obvious trivial cases, as they can be monitored uniquely by a single array spot. Of the remaining transcripts, those that share their minimum degeneracy oligo with only trivial genes are also trivial by this association. Statistically, a sufficiently large fraction of genes having a minimum degeneracy of 1 should render all genes trivial. Modifications to our purely analytic model fail to make accurate predictions for small subsets of oligonucleotides, presumably owing to the underlying non-randomness of real genomes. However, beginning only with a histogram of the minimum degeneracy values for all genes in an organism (Figure 3), it is easy to estimate the likelihood of the above associations and to predict the total fraction of genes whose expression levels can be solved trivially (see Methods). To check these predictions, we wrote a computer program to determine exactly the fraction of trivially solvable genes based on the individual gene sequences.

Figure 3.

Minimum degeneracy histograms for mouse assuming 1 mismatch. (A) 11-mers, no truncation; (B) 11-mers, truncation to 50 bp; (C) 12-mers, no truncation; (D) 12-mers, truncation to 100 bp. Each histogram shows the fraction of transcripts having a given minimum degeneracy value. Histograms were generated by custom computer software that examined actual sequence data to find the n-mer with lowest degeneracy that binds to each transcript (allowing up to 1 mismatch). As expected, increasing n and decreasing transcript length both increase the proportion of genes having low minimum degeneracy.

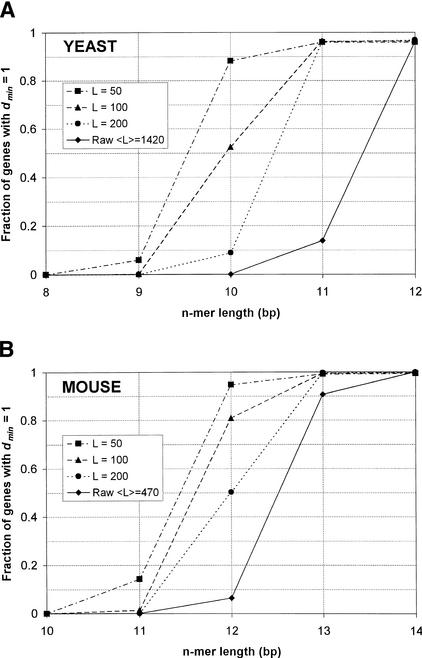
A few results for the case of one mismatch are summarized in Table 2. In general, we found that nearly all genes turn out to be trivial if the fraction of genes having minimum degeneracy of 1 (Figs. 4A,B) is at least ∼80%. With a 10-mer array and transcript truncation to 50 bp, 98.8% of yeast transcripts are trivial. Most of the non-trivial genes are in fact unsolvable because they have identical sequences after truncation. Omitting the truncation would eliminate this problem and also simplify the experimental protocol. No truncation is needed with a 12-mer array, in which case 99.8% of transcripts are trivial. On close inspection, we found that most of the non-trivial genes may actually be unsolvable because they differ by only a few base pairs from one another. Similar results were obtained for mouse. With a 12-mer array and truncation to 100 bp, 97.9% of mouse transcripts are trivial; with a 13-mer array and no truncation, 99.6% of mouse transcripts are trivial. Note that these n values for both yeast and mouse are lower (by 1 or 2 bp) than the previous predictions, which were based on the average degeneracy taken over all n-mers. It is likely that even smaller arrays can be used if one is willing to expend more computational effort and address also the non-trivial cases.

Table 2.

Fraction of Genes That Can be Trivially Solved and Inherent Redundancy for Several Useful Array Sizes (Assuming Single Mismatches)

Organism	n	Truncation	Fraction with minimum degeneracy of 1	Fraction trivial (predicted)	Fraction trivial (actual)	Inherent redundancy
yeast	10	50 bp	0.887	0.988	0.987	10.96
yeast	12	none	0.966	1.000	0.998	54.14
mouse	12	100 bp	0.809	0.996	0.979	6.17
mouse	13	none	0.906	1.000	0.996	20.28

Figure 4.

Fraction of transcripts having minimum degeneracy equal to 1 (i.e., containing an oligo not found in any other transcripts) over a range of n-mer sizes and truncation lengths L, assuming 1 mismatch for yeast (A) and mouse (B). Raw designates untruncated cases. It turns out that when a sufficient fraction of transcripts have minimum degeneracy d_min equal to 1, nearly all gene expression levels can be solved trivially.

Redundancy

Generally, microarrays using oligonucleotides require more than one probe per gene to produce reliable results. With the decreased feature sizes and shorter probe lengths of combinatorial n-mer arrays, the importance of redundancy is likely to be greater. Thus, although in principle only a single oligo is needed to monitor each gene, in practice one would use multiple oligos to allow averaging over independent measurements.

An approximate measure of the inherent level of redundancy in an array is the average number of unique oligos per gene. This quantity can be predicted by dividing the total number of unique oligos (determined from either the Poisson model or the actual genomic data) by the number of genes. For the four array sizes discussed in the previous section, the average redundancy is on the order of ten unique oligos per gene (see Table 2).

To ensure that a high fraction of genes have at least ten unique oligos per gene, computing the average is insufficient; the fraction must be calculated directly from the genomic sequence data. For yeast with one mismatch, an 11-mer array with truncation to 100 bp ensures that 97.0% of genes bind to at least ten unique oligos. A 13-mer array with truncation to 200 bp ensures that 99.6% of genes bind to at least ten unique oligos in mouse with one mismatch.

CONCLUSIONS

Because the mouse genome is only slightly smaller than the human genome, the above results provide an estimate of the required size for a universal array, namely n ⩾ 12 for truncated transcripts or n ⩾ 13 for untruncated transcripts. To ensure a redundancy of at least 10 unique oligos per gene, the required size is n ⩾ 13. All figures are well within the limit of practical fabrication and readout (n ⩽ 16). Arrays as small as n = 10 should be universal for organisms up to the complexity of yeast.

In addition to universality, combinatorial n-mer arrays offer other significant advantages. For instance, because selection of n-mers with which to identify transcripts is performed in software, data can be reanalyzed (avoiding additional experiments) as genomic sequence data is updated. The selection criteria can be modified easily to incorporate additional constraints on parameters, such as spot quality and melting temperatures, to yield higher quality measurements. Besides gene expression analysis, combinatorial n-mer arrays have potential application in such diverse areas as DNA sequencing by hybridization (Drmanac et al. 1998), the study of DNA binding proteins (Bulyk et al. 1999), and genomic fingerprinting (Landegren et al. 1998).

As a final note, we point out that whereas combinatorial n-mer arrays can be fabricated without genomic knowledge, our analysis strategy does make use of known genomic sequence data as a prerequisite for interpreting the data. This data now exists in an essentially complete form for several bacteria, yeast, worm, fly, mouse, human, and many others. For unsequenced organisms, we believe that it may be possible to deduce partial gene expression information without prior genomic knowledge by performing multiple hybridization experiments.

METHODS

Mathematical Analysis of Gene Expression

A hybridization experiment can be expressed as the matrix equation S = H·E, in which S = (S₁,S₂,…,S_i,…,S_No)^T is the vector of measured signal intensities and E = (E₁,E₂,…,E_i,…,E_Ng)^T is the vector of unknown transcript concentrations (i.e., expression levels). For a particular set of hybridization conditions, H is a constant matrix if the system is in chemical equilibrium and the array is not saturated. Each coefficient H_ij of H is closely related to the melting temperature (affinity) of the binding interaction between transcript j and oligo i and can be estimated using semi-empirical formulae (Breslauer et al. 1986; Hartemink and Gifford 1997) or can be measured by calibration experiments with known quantities of various mRNA species. Deducing transcript expression levels is reduced to the computational problem of solving the above system of equations for E. Because it is impractical to invert H directly, our approach is to find a projection P such that H‘ = P·H is a square N_g×N_g matrix. The vast reduction in dimensionality allows one considerable freedom in choosing a projection and choosing P such that H‘ is invertible and in block diagonal form permits trivial determination of expression levels, E = (P·H)⁻¹·(P·S) = (H‘)⁻¹·S‘. We search for a projection beginning with the minimum degeneracy oligo for each gene then selecting additional oligos until H‘ is invertible.

Source of Sequence Data

Genomic sequence data for degeneracy calculations was drawn from public gene sequence databases for two organisms, yeast (Saccharomyces cerevisiae) and mouse (Mus musculus). These two organisms were selected because of their availability and because they are representative of the two ends of the eukaryotic genome-size spectrum.

Yeast sequence data was obtained from the Saccharomyces Genome Database at Stanford University (http://genome-www.stanford.edu/Saccharomyces/). We downloaded the complete set of coding sequences at ftp://genome-ftp.stanford.edu/pub/yeast/yeast_ORFs/orf_coding.fasta.Z on December 14, 1999. For this database, N_g = 6306 and ℓ ≈ 1420. Because identical gene sequences cannot be distinguished by any microarray, duplicates were removed, leaving N_g = 6276 unique genes.

Sequences for mouse were downloaded from the UniGene System at the National Center for Biotechnology Information (http://www.ncbi.nlm.nih.gov/UniGene/). We downloaded the file ftp://ftp.ncbi.nlm.nih.gov/repository/UniGene/Mm.seq.uniq.Z, Build 74. Although this database does not contain the complete mouse genome, it contains both genes and ESTs representing a substantial portion of the expressed genome. For this database, N_g = 75963 and ℓ ≈ 471. Owing to the many ESTs, the average transcript length is quite small. Thus, we included some calculations with a longer hypothetical average gene length.

Degeneracy Calculations

To calculate degeneracy values from actual sequence data, we wrote a computer program that scans through the sequences composing a transcriptome and tallies the number of times each subsequence of length n (n-mer) is encountered in different transcripts. Accounting for length truncation to length L is accomplished by examining only the first L characters of each transcript. To deal with mismatches, each subsequence of length n within a transcript is expanded into a set of all sequences that differ by at most m nucleotides from the original subsequence. Sequences containing characters other than A,C, G, and T were ignored (0% of sequence data in yeast; 1%–2% in mouse). From the list of degeneracy values for each of the 4ⁿ possible n-mers, the average degeneracy is calculated easily for comparison with the analytic model. In addition, the degeneracy list itself is used to generate a histogram showing the fraction of n-mers having each degeneracy value, for comparison with theoretical histograms calculated from Equation 1.

Predicting the Fraction of Solvable Expression Levels

The fraction of trivially solvable expression levels was estimated in a probabilistic fashion from a minimum-degeneracy histogram derived from actual sequence data (e.g., Fig. 3). These histograms were generated by a computer program that makes use the list of n-mer degeneracies to determine the lowest degeneracy oligo to which the transcript can bind. A minimum-degeneracy histogram indicates the fraction of genes x_i having each value of minimum degeneracy i.

Genes having minimum degeneracy equal to 1 are clearly trivial because their expression level can be deduced unambiguously from the fluorescence of the minimum degeneracy oligo. A fraction x₁ of all transcripts fall into this category. Those genes having minimum degeneracy equal to 2 are trivial if the other gene that shares the degeneracy 2 oligo has minimum degeneracy equal to 1. Of all transcripts, a fraction x₂·x₁ is expected to fall into this category. Similarly, those genes having minimum degeneracy equal to 3 are trivial if both of the other (distinct) genes that share the degeneracy 3 oligo have minimum degeneracy equal to 1. Statistically, a fraction x₃·x₁·(x₁−1/N_g) of genes should fall into this category. Continuing in this fashion, one obtains a summation that estimates the fraction of genes whose expression level can be solved trivially.

A computer program was written to examine actual gene sequences to determine the exact total fraction that could be solved trivially. As above, all genes having minimum degeneracy equal to 1 are clearly trivial. Each of the remaining genes is handled in the following manner. First, all n-mers to which the gene binds are identified and sorted in increasing order of degeneracy. Then, for each n-mer in turn, the other genes that bind the n-mer are identified. If all of these other genes have minimum degeneracy equal to 1, then the original gene is trivial by its association. If this condition is not met for any of the n-mers with which the gene binds, then the gene is declared non-trivial.

The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.