Estimating Coarse Gene Network Structure from Large-Scale Gene Perturbation Data

Abstract

Large scale gene perturbation experiments generate information about the number of genes whose activity is directly or indirectly affected by a gene perturbation. From this information, one can numerically estimate coarse structural network features such as the total number of direct regulatory interactions and the number of isolated subnetworks in a transcriptional regulation network. Applied to the results of a large-scale gene knockout experiment in the yeast Saccharomyces cerevisiae, the results suggest that the yeast transcriptional regulatory network is very sparse, containing no more direct regulatory interactions than genes. The network comprises >100 independent subnetworks.

Estimating the coarse structure of genetic networks is necessary to solve a wide variety of problems in genome biology. These range from network reconstruction—reconstruction would be straightforward for some network architectures, but excruciating for others (Weaver et al. 1999; Ideker et al. 2000; Wagner 2001a)—to a plethora of open biological questions that eluded pregenomic biology. They regard the degree to which genes have pleiotropic effects, the modularity of genetic networks, and the amount of cross-talk in biochemical pathways. But estimating coarse genetic network structure has a catch: How does one characterize a network's structure before having reconstructed the network? I propose a statistical solution to this problem. Like most statistical approaches it has a caveat: It requires assumptions about network features, assumptions that cannot be rigorously validated until a network is completely reconstructed.

Before introducing this approach, I need to introduce some terminology. For the purpose of this paper, I define a genetic network as a group of genes in which individual genes can change the activity of other genes. What, then, is a change in gene activity? It might include changes in gene expression (on the mRNA or protein level), methylation state, phosphorylation state, or alternative splicing. I will restrict myself here to mRNA expression as measured by microarrays (Lockhart and Winzeler 2000) as the notion of gene activity and its change in response to a genetic perturbation. However, the principal idea applies to any notion of gene activity. When manipulating a gene that affects the activity of other genes, whether by mutation, overexpression, or any other means, one can ask whether this effect is due to a direct or an indirect interaction. For example, when overexpressing a transcription factor X, I might find that the expression level of genes A and B change. On further investigation, I may find that X binds the upstream regulatory region of A and up-regulates its expression. This is what I call a direct effect of X on A. However, in the case of B, I might find that X induces the expression of a protein phosphatase that dephosphorylates and thus inactivates a transcriptional repressor of B. This is what I call an indirect effect of X on B.

What is the most useful mathematical representation to estimate the coarse structure of a genetic network? Candidate representations include differential equation models (Reinitz 1995, 1999; von Dassow et al. 2000), Boolean switching networks (Kauffman 1967; Somogyi et al. 1997; Dhaeseleer et al. 2000; Ideker et al. 2000), and graph models. The first class of models requires a detailed network wiring diagram and information on many biochemical parameters. It is aimed at describing gene activity dynamics and, therefore, has too high a level of resolution for my purpose. Switching networks assume either that genes can only be in one of two states, on or off. Although cooperative gene interactions are pervasive in gene regulation, the limiting case of discrete switch-like regulation may be the exception rather than the rule. This is evident from numerous microarray studies of genetic networks (Chu et al. 1998; Spellman et al. 1998; Iyer et al. 1999), where thousands of genes show continuous—not discrete—mRNA expression changes in response to environmental and genetic changes.

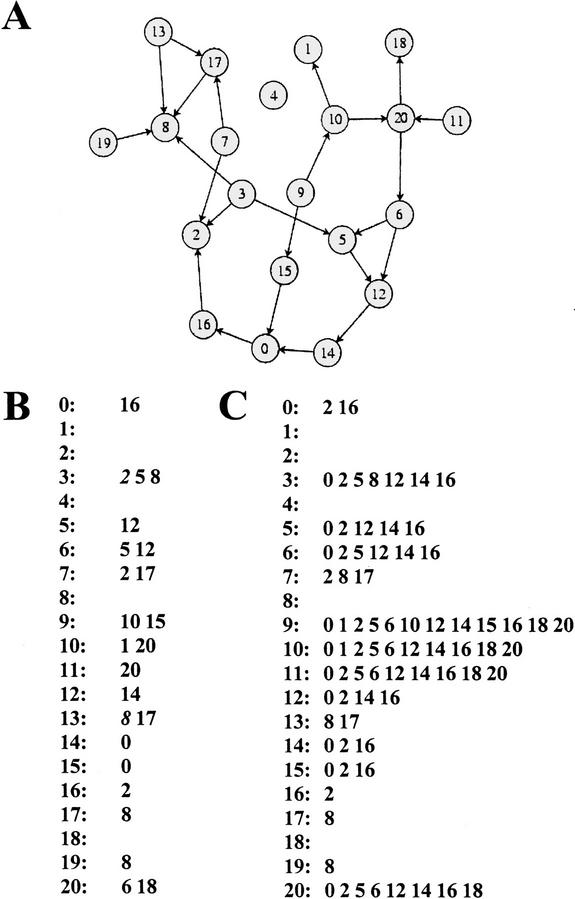
Lastly, a graph model requires only information on which genes affect each other directly in their activity. Its low level of resolution is ideal for my purpose, especially given the inherent noise of the gene expression data I will be using. More specifically, I will use a directed graph or digraph model, which is a mathematical object consisting of nodes and directed edges. In a graph representation of a genetic network, the nodes of the graph correspond to genes, and two genes, say gene 1 and gene 2, are connected by a directed edge (an arrow, 1→2) if gene 1 influences the activity of gene 2 directly. Figure 1A shows a graph representation of a hypothetical genetic network of 21 genes. Figure 1B shows an alternative representation of the network shown in 1A. For each gene i, Figure 1B contains a list of genes whose activity is directly influenced by gene i. One might also call this the list of direct regulatory interactions. It completely defines the structure of the graph.

Figure 1.

Direct and indirect perturbation effects in a genetic network. (A) Genetic network represented as a graph whose nodes correspond to genes numbered from 0 through 20. Two genes are connected by an arrow if they influence each other's activity directly. (B) List of direct regulatory interactions in the network. For each gene i (to the left of the colon), it is the list of all genes directly influenced by i. (C) List of direct and indirect perturbation effects for the network in A. When perturbing the activity of a gene i in the network, all genes whose activities are directly or indirectly influenced by this gene will change their activity. For each perturbed gene, one gets this list by following all paths leaving a gene along the arrows shown.

Genetic perturbation experiments cannot distinguish direct from indirect interactions. That is, when perturbing a gene in the network shown in Figure 1A, one would identify all genes that this perturbation affects directly or indirectly as its effects ripple through the network. For the hypothetical network of Figure 1, the genes affected by perturbing a gene are shown in the list of Figure 1C. This list can be obtained from Figure 1A by following all paths of arrows starting at a perturbed gene.

In the context of this representation, I am asking the following question. When given information on the number of genes whose activity changes—directly or indirectly—through a genetic perturbation, can one say anything about the structure of the underlying graph, the underlying genetic network? That is, given information like that in Figure 1C, can one say anything about the structure of the network as defined in Figure 1A and B? The answer is yes, if one is willing to make assumptions about coarse statistical features of a genetic network. (Any large genetic network has such features, the question is just what they are.)

RESULTS

In the absence of other information, the most parsimonious assumption about the distribution of direct interactions in the graph is that of a random graph with a given number of edges, where any two nodes are equally likely to be connected by an edge. Such graphs are known as Erdős-Rényi (ER) random graphs (Bollobás 1985). Recent analyses on cellular circuits as diverse as metabolic networks (Fell and Wagner 2000; Jeong 2000; Wagner and Fell 2001) and a microbial protein interaction network (Wagner 2001b) show that these cellular networks share commonalities with ER random graphs, such as their short path lengths. However, a conspicuous deviation regards the distribution of the number of direct interactions per node in these networks. In the ER model, this number follows a Poisson distribution. However, in the studied cellular networks this number follows a broad-tailed power law distribution, where the likelihood that a randomly chosen node from the network has d direct interactions is P(d) ∝ d^−τ (1.5 < τ < 2.5) (Fell and Wagner 2000; Jeong 2000; Wagner and Fell 2001; Wagner 2001b). Such networks have not only a wider range of direct interactions per node, they also have a greater number of nodes with many direct interactions than ER networks. For transcriptional regulation networks (where gene perturbations influence mRNA gene expression patterns) such broad-tailed distributions meet an important biological objection to the ER model. It is that regulatory networks should consist of regulatory genes, genes that directly influence the activity of many genes, and other genes that influence the activity of few or no genes.

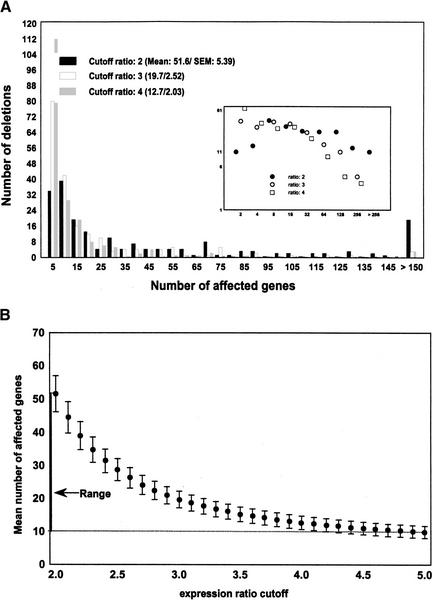
Here, I use both the ER assumption and that of a broad-tailed distribution of direct regulatory interactions to coarsely estimate the connectivity, that is, the number of direct interactions in a transcriptional regulation network. I include the ER model because the number of direct interactions estimated from it is larger than for any of the broad-tailed models considered. In this sense, it provides a maximal estimate of the number of direct interactions. The data for the estimate come from a recent large-scale gene perturbation experiment in the yeast Saccharomyces cerevisiae, in which 271 yeast genes were deleted (Hughes et al. 2000). The authors assessed the effect of each deletion on the mRNA expression level of 6312 yeast genes on synthetic complete medium (SC) using cDNA microarrays (Hughes et al. 2000). More specifically, for each genetic perturbation and for each of 6312 genes, they determined a ratio r = w/d of the relative expression level of a gene in the wild-type, w, and after a gene deletion, d. As microarray gene expression measurements are notoriously noisy, it is not clear what ratio r assures that a gene's expression has changed significantly relative to the wild type. It is thus necessary to choose a threshold R beyond which an expression ratio is deemed significant. In the absence of rigorous statistical methods to determine an appropriate R, I will allow R to range between 2 (least conservative) and 5 (most conservative) and report only results unaffected by changing R. Figure 2A shows the distribution of the number of genes affected by a gene deletion for varying values of R, the cutoff-ratio, in this data set. Figure 2B summarizes this distribution by showing means and standard errors of the number of genes affected by a perturbation, as R is varied from 2 to 5. On average, a genetic perturbation affects the mRNA expression level of between 9.9 (R = 5; S.E. = 1.84) and 51.6 (R = 2; S.E. = 1.89) genes. This range of values is the key ingredient to the following analysis.

Figure 2.

Number of genes affected by a genetic perturbation. (A) Distribution of the number of genes whose mRNA expression levels changes as a result of a gene deletion for three different significance thresholds R of expression ratios. (Inset) Same distribution on a log–log scale. (B) Mean and standard error of the mean (S.E.M.) of the number of genes whose expression ratio is affected by a genetic perturbation as a function of the significance threshold R. Averages are taken over the 196 genetic perturbations reported in (Hughes et al. 2000). The mean number of affected genes varies between 9.9 (R = 5; S.E.M. = 1.84) and 51.6 (R = 2; S.E.M. = 1.89) genes.

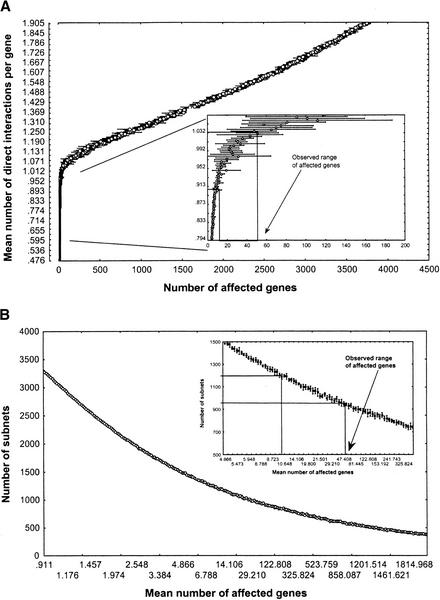
Figure 3A shows the relation between the mean number of direct interactions per gene (y-axis) and the number of genes affected by a genetic perturbation (x-axis) for Erdős-Rényi networks of n = 6300 genes. The inset also shows the experimentally observed range (from Fig. 2B) of the mean number of genes whose mRNA expression is affected by a gene deletion. This range maps onto a narrow interval of direct regulatory interactions d per gene (0.9 < d < 1.05, approximately). Thus, the yeast transcriptional regulatory network appears very sparse, showing no more direct regulatory interactions than genes. (The maximally possible number of inter actions would be 1.9 × 10⁷, three orders of magnitudes higher.)

Figure 3.

Connectivity and module number in ER networks. (A) Mean number of direct interactions per gene (y-axis, the connectivity of the network) as a function of the mean number of genes affected by a genetic perturbation (x-axis). (Inset) Same relation for a part of the connectivity range, together with the experimentally observed range of the mean number of genes whose expression is affected by a gene deletion (Fig. 2B). This range maps onto a narrow interval of direct regulatory interactions, d, per gene (0.9<d<1.05, approximately). (B) Number of subnets in a random network as a function of the number of genes affected by a genetic perturbation. (Inset) Same relation for a part of the range, together with the experimentally observed range of genes affected by a perturbation.

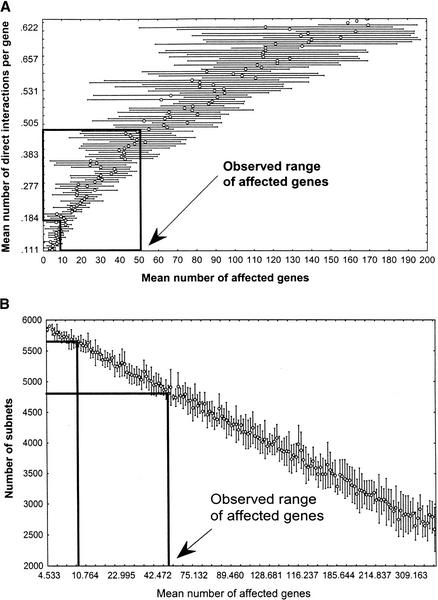
In comparison with ER networks with the same number of direct interactions, networks with a broad-tailed degree distribution generally show greater mean and variance in the number of genes affected by a perturbation. The reason lies in their disproportionately large number of genes with many direct interactions. This is exemplified by Figure 4A, which shows numerical estimates from a network with n = 6300 genes whose degree distribution follows a power law with τ = 2, an exponent within the range found for other biological networks (Barabasi and Albert 1999; Fell and Wagner 2000; Jeong 2000; Wagner 2001b; Wagner and Fell 2001). Networks with lower τ have even lower connectivity, but even networks with higher τ would have lower connectivity than ER networks. For τ = 2 the estimated number of direct interactions per gene falls within a range of 0.15 < d < 0.5 (Fig. 4A).

Figure 4.

Connectivity and subnet number in networks with power law degree distribution. (A) Mean number of direct interactions per gene (y-axis, the connectivity of the network) as a function of the mean number of genes affected by a genetic perturbation (x-axis). (B) Number of subnets in a random network as a function of the number of genes affected by a genetic perturbation. (Boxed regions) Upper and lower boundaries of the mean number of genes affected by a perturbation, according to experimental data (Hughes et al. 2000, Fig. 2B). The corresponding range of subnets is 4584–5638 (σ = 153 and σ = 92, respectively), most of which are isolated genes. Notice that the scale of both x-axes corresponds approximately to that of the insets in Fig. 3.

Gene perturbation data can also be used to derive a coarse picture of other network features. One such feature is the number of modules or subnets of a network, groups of genes that influence only each others expression, but not that of other genes.

More precisely, I define a subnet as a weak component of a graph, a group of genes where any two genes are connected through a path regardless of edge orientation (for a formally rigorous definition, see Harary 1969). Figure 3B shows the number of subnets as a function of the number of genes affected by a genetic perturbation for ER networks. For a network with 9.9 < a < 51.6 genes affected by a genetic perturbation, this relation implies between 1282 (σ = 16.8; a = 9.9) and 956 (σ = 31; a = 51.6) subnets, respectively. Many of these subnets are isolated genes, genes neither transcriptionally regulated nor regulating the mRNA expression of any other gene. More specifically, the expected number of isolated nodes in a sparse ER network with n nodes and k = nd edges is approximated by n₀ ≈ n[1−2k/(n(n−1))]ⁿ⁻¹. For an ER network, this leads to an estimated mean number of 185–241 subnets containing more than one gene (1282 − 1041 = 241 for a = 9.9 and d = 0.9; 956 − 771 = 185 for a = 51.6 and d = 1.05). Figure 4B shows analogous numerical results for networks whose interactions follow a power-law (τ = 2), and leads to a predicted number of 144–349 subnets containing more than one gene.

DISCUSSION

Crude estimates of gene network structure as obtained here begin to approach biological questions, for example, whether genetic networks have a modular organization, or whether they are globally connected. Put differently, to what degree do genes have pleiotropic effects when mutated? While the estimated number of modules in this network has formidable error margins and depends on statistical assumptions about network architecture, the network may well comprise hundreds of modules. This and the fact that there are many isolated genes makes global connectedness and pervasive pleiotropy unlikely.

Complementary if anecdotal evidence is available from a variety of sources. First, a study of 225 genotypes of Escherichia coli carrying one, two, or three mutations showed that a sizable fraction of mutations affect fitness independently from each other (Elena and Lenski 1997). This argues against the concept of pervasive pleiotropy. It is consistent with the idea of sparse genetic networks with multiple subnets that affect fitness independently. Suggestive are also the results of numerous microarray experiments showing that genes fall into clearly distinguishable coexpressed clusters (Chu et al. 1998; Eisen et al. 1998; Spellman et al. 1998; Iyer et al. 1999; Lockhart and Winzeler 2000). The third class of evidence comes from the large scale analysis of physical interactions among gene products in yeast (Ito et al. 2000; Uetz et al. 2000). Despite significant caveats to the available data (it collapses spatial and temporal dimensions onto a static network image, and may contain substantial amounts of error), the data suggest that the yeast protein interaction network consists of a disproportionately large subnetwork and >100 smaller subnetworks (Wagner 2001b). A different story is told by the connected network of core intermediate metabolism (Fell and Wagner 2000; Wagner and Fell 2001). The reasons for its connectedness, however, may be specific to metabolism: Metabolism provides energy and biochemical building blocks that are necessary at all times and in all environments, albeit in different amounts. It thus may need to be able to react as a whole to environmental perturbations.

There are a number of caveats to the estimates made here. First, the graph model used here certainly provides only the crudest of network caricatures. It is adequate given the limitations of the data used, but neglects many important factors that would influence the dynamics of gene activity, such as quantitative differences in strengths of interactions, and various control structures such as feedback loops that may be of great importance in influencing gene activity dynamics (Omholt et al. 2000). In addition, one might argue that the restriction to transcriptional regulation networks (imposed by experimental technology) compromises biological interpretation of network structure estimates. In this regard, it is worth keeping in mind that transcriptional regulation is ubiquitous and that the endpoint of most regulatory pathways are transcriptionally regulated genes. Thus, while imperfect, a transcriptional regulation network provides a backbone around which more inclusive analyses can be organized.

Second, the number of modules and the number of isolated genes are likely underestimates, because gene perturbation studies (Hughes et al. 2000) preferentially perturb a sample of interesting regulatory genes with many interactions and not an unbiased random sample.

Third, limits of experimental resolution make a flawless detection of all indirect interactions impossible. For instance, competing effects of the same knockout mutation on different pathways in the network might compensate for each other at a gene's promoter, resulting in a small overall change of the gene's expression level. The fraction of such genes is difficult to estimate. However, the enormous success of perturbative approaches in dissecting biochemical pathways suggests that this fraction is not very large. The liberally chosen lower threshold of R=2 may also alleviate the problem. By using it, even genes whose expression level does not change drastically are included in the analyzed data.

The number of direct regulatory interactions in this network is of the order of the total number of genes. It may be much smaller if few genes are responsible for most interactions. The global yeast transcriptional regulatory network is thus very sparse. The cardinal weakness of the approach used to obtain this estimate is the need to make an assumption—currently ad hoc, although supported anecdotally—about global network structure. However, the main result of sparse network connectivity is robust to changes in assumptions about this network structure. That genetic networks are very sparse is good news for methods to reconstruct them—without statistical assumptions—from perturbation experiments (Weaver et al. 1999; Ideker et al. 2000; Wagner 2001a).

METHODS

Data summarizing the effects of 271 gene deletions (and other treatments) on gene expression was made available as supplemental material to Hughes et al. (2000; file data-expts-1-300- ratios.txt). From this data set, which contains log₂-transformed expression ratios of 6312 strains for each mutation, I eliminated all data on haploid and aneuploid deletion strains, as well as data on nongenetic treatments. I analyzed the remaining data set of the effects of 196 gene deletions on the expression 6312 yeast genes. In analyzing this data, I have not distinguished between perturbations of transcriptional activators and that of other genes, as there does not seem to be a clear distinction with respect to their perturbation effects. For instance, one might expect that perturbation of transcription factors affects more genes than other perturbations. However, among the 10 functionally characterized genes whose null mutation affects the mRNA levels of the most other genes, there is only 1 bona fide transcriptional activator (SWI4). Two others may have indirect roles in transcriptional regulation, that is, in mRNA turnover (MRT4) and histone acetylation (HDA1).

The random networks considered in Figure 3 are Erdős-Rényi (ER) random graphs, where any pair of n nodes (genes) is equally likely to be connected by one of k directed edges (Bollobás 1985). Random graph generators used are based on Mehlhorn and Naher (1999; section 3.2.2). A subnet corresponds to a weak component (Harary 1969) of a graph. The number of subnets for an ER random graph with given n and k was calculated following (Mehlhorn and Naher 1999). The number of isolated nodes in a sparse random graph with n nodes and k edges can be estimated as n₀ ≈ n[1−2k/(n(n−1))]ⁿ⁻¹.

The networks analyzed in Figure 4 are random graphs whose probability distribution P(d) of the number of direct interactions is proportional to d^−τ, for τ = 2. Such graphs, with a prespecified number of n = 6300 nodes and varying numbers of k edges were generated following a prescription by M. Newman (unpubl.). Briefly, a graph with n = 6300 isolated nodes was generated. A node was then chosen at random from this graph. A random integer d > 0 with the desired power law distribution was then assigned to this node in the following way. First, a random number d =  ⌈−γ*log(1 − r)⌉ was generated, where r is a random real number uniformly distributed in the interval (0,1), and γ > 0 is a constant (see below). The symbol ⌈x⌉ refers to the smallest integer greater than x. Second, this number d was accepted with probability d^−τ. If d was not accepted, it was discarded, and a new d was generated according to the same prescription, repeating this process until a d was accepted. Strictly speaking, the resulting distribution of d is a power law with an exponential cutoff, P(d) ∝ d^−τexp(−d/γ). (Such a cutoff is necessary for graphs with τ < 2. They are otherwise ill-defined, because their distribution P(d) diverges.) A large value of γ = 1000 was used here, such that the distortion caused by the cutoff is negligible. Once a d was accepted, it was assigned to the randomly chosen node. Another node was chosen at random (without replacement), an integer d was assigned to it in the same way, and this process was repeated until the sum S of all the integers assigned to the chosen nodes first exceeded 2k. The integers assigned to each node correspond to the node's degree. They may also be thought of as the stubs of edges emerging from a node. Two such stubs were then chosen at random, and the respective nodes were connected via an edge, until the reservoir of stubs was exhausted, that is, until S/2 edges had been placed on the graph.

For both ER random graphs and random graphs with power-law degree distributions, each data point shown in Figures 3 and 4, respectively, is a numerical estimate based on the mean number of affected genes (horizontal bars correspond to standard deviations) over 10 numerically generated networks with n=6300 genes. For each of the 10 networks, the mean number of genes affected by a perturbation (i.e., reachable from a gene) was determined exhaustively via a breadth-first search algorithm (Mehlhorn and Naher 1999).

The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.