Abstract
Background
The hallmarks of age-related macular degeneration, the leading cause of blindness in the developed world, are the subretinal deposits known as drusen. Drusen identification and measurement play a key role in clinical studies of this disease. Current manual methods of drusen measurement are laborious and subjective. Our purpose was to expedite clinical research with an accurate, reliable digital method.
Methods
An interactive semi-automated procedure was developed to level the macular background reflectance for the purpose of morphometric analysis of drusen. 12 color fundus photographs of patients with age-related macular degeneration and drusen were analyzed. After digitizing the photographs, the underlying background pattern in the green channel was leveled by an algorithm based on the elliptically concentric geometry of the reflectance in the normal macula: the gray scale values of all structures within defined elliptical boundaries were raised sequentially until a uniform background was obtained. Segmentation of drusen and area measurements in the central and middle subfields (1000 μm and 3000 μm diameters) were performed by uniform thresholds. Two observers using this interactive semi-automated software measured each image digitally. The mean digital measurements were compared to independent stereo fundus gradings by two expert graders (stereo Grader 1 estimated the drusen percentage in each of the 24 regions as falling into one of four standard broad ranges; stereo Grader 2 estimated drusen percentages in 1% to 5% intervals).
Results
The mean digital area measurements had a median standard deviation of 1.9%. The mean digital area measurements agreed with stereo Grader 1 in 22/24 cases. The 95% limits of agreement between the mean digital area measurements and the more precise stereo gradings of Grader 2 were -6.4 % to +6.8 % in the central subfield and -6.0 % to +4.5 % in the middle subfield. The mean absolute differences between the digital and stereo gradings 2 were 2.8 +/- 3.4% in the central subfield and 2.2 +/- 2.7% in the middle subfield.
Conclusions
Semi-automated, supervised drusen measurements may be done reproducibly and accurately with adaptations of commercial software. This technique for macular image analysis has potential for use in clinical research.
Background
Color fundus photographs have been routinely employed for diagnostic purposes for many years, and fundus photo gradings are central to clinical studies of macular disease [1,2]. The natural history of age-related macular degeneration (AMD), the leading cause of blindness in the developed world [3], is in particular tied to that of subretinal deposits known as drusen [4-12]. Drusen are key in the classification of AMD, hence the importance of drusen identification and measurement in clinical studies. The classification of patients by stage of age-related maculopathy involves painstaking analysis of drusen size, number, area and morphology in several subcategories. Significant effort has been placed in developing and validating the International [1] and Wisconsin [2] Grading Systems. The systematic study of drusen resorption following laser photocoagulation also underscores the importance of drusen measurement and recognition. [8-10,13-16].
There has been continued interest in the use of digital techniques for quantification of macular pathology, particularly drusen, over the last two decades [17-25]. However, despite progress, none of these methods have gained widespread use. A major obstacle has been that the reflectance of the normal background, on which the pathology is superimposed, is inherently non-uniform. In particular, the normally less reflectant central macula is superimposed on whatever the underlying or "true" drusen reflectance might be. Hence, given two anatomically identical drusen, one in the center of the macula and one at 3000 μm, the observer will see them differently in the fundus photograph. The outlying drusen will appear brighter and larger than its identical counterpart. The human eye with training makes allowances for this variability, but a computer applying a threshold does not.
Prior methods have so far been unable to deal with this non-uniform macular background reflectance as a whole. An early study [25] used adaptive thresholding techniques on 1024 separate windows of 8 × 8 pixels. Perivascular windows sometimes incorrectly interpreted bimodal distributions as coming from perivascular drusen. Large areas of background were also sometimes included due to incorrect choices of threshold. These sources of error required many operator interventions to correct. The result was a method that was capable of excellent reproducibility (+/- 2.3 %), but was too tedious for general use. Hence, as early as 1986 the limiting factor was not the time complexity of computer algorithms, but the fact that the method itself was tied to local reflectance calculations. This problem persisted in a recent study that relied on applying local thresholds to regions ranging from 20 to 100 pixels square [17]. Drusen were identified first by checking the local histogram for sufficient skewness (equivalent in this method to determining that drusen were present in the region) and then setting a local threshold. However, the method was defeated if a large drusen dominated a local region. In this case the local distribution would not be skew, and the large drusen would be completely missed. A user would be required to correct this error manually after the automated segmentation. In general, a post-processing step was necessary to correct drusen segmentation errors or enlarge incompletely segmented drusen to achieve acceptable accuracy. These studies demonstrate that segmentation by local histograms and threshold techniques has serious deficiencies.
Rapantzikos [18] et al have used other morphological operators as well as varying local histogram criteria for threshold choice to try to correct these deficiencies. Their criteria involve kurtosis as well as skewness. The fundamental fact remains, as they readily admit, no matter how many histogram-based criteria are employed for local segmentation, that widely different combinations of image features (drusen and background) can yield the same histogram. An extreme example, as in [17], would be regions that were either all background or all drusen, in either case yielding the same mesokurtic nonskewed distribution. Their solution, a morphological dilation operator, is intended in the all drusen case to distort the local histogram by reintroducing background and thereby improve threshold recognition. It is unclear, however, that this artificial operator will always perform as intended. Another example of the arbitrary application of a general tool occurs when their segmentation leaves isolated bright groups of pixels. They conclude if these are in close proximity, then they possibly belong to the same large drusen and therefore must be expanded by a closing operator. But these could also be isolated small hard drusen. Lastly, despite the use of a wide range of general image analysis tools, their methods, as those in the other references, take no account of the intrinsic background variability, and accordingly can produce errors in a systematic and predictable fashion: inadequate segmentation centrally and over inclusive segmentation in the peripheral macula, as their own illustrations demonstrate.
An alternative to color photography is scanning laser ophthalmoscopy (SLO) imaging for recognition of bright features. This method has been used for detection of retinal exudates in diabetes [19] using a single optimized wavelength. The concept has been carried further in a multispectral approach using a tunable dye laser [20]. The problem of variable illumination and/or intrinsic background variability is also addressed by multiple local adaptive thresholds, but with a novel addition. Regions of the image are designated as "featureless" if the coefficient of variation of the local histogram is sufficiently small. The mean gray scale values of these regions are then used to determine local thresholds, which are then interpolated to give a global threshold function. Since diabetic exudates tend to be smaller than soft drusen, it is unclear if sufficient featureless windows would be available in an image with multiple soft drusen to apply this method.
Our approach to this problem has been as follows. We first demonstrated that there was an inherent geometric pattern to the background reflectance in normal fundus images [26]. We then developed a semi-automated interactive method based on these patterns to level the background reflectance of a drusen-containing image independent of the reflectivity of the overlying drusen (preliminary results presented in abstract form [27]). This allows the use of a global threshold to segment the drusen accurately. By adopting this unified approach to the macular reflectance problem, we avoid the multiple local thresholds used in previous approaches [17-20,24,25]. It is important to note, however, that our method is not the standard technique of shadowing by subtracting or dividing by a blur image. These standard techniques [28] (also used herein) are useful for shading correction on large scales. As we have shown in our previous work [26], however, the macular reflectance can change significantly over ranges of distance (50–100 μm) comparable to the size of pathologic structures of interest. Hence, subtracting the variation on this scale would tend to remove such structures from the image. Indeed, one reason we are presenting our particular method is that we found after many trials and errors that none of the standard morphological transform routines (dilations, erosion, closings) or combinations thereof, were able to precisely define the boundary of pathological features in a fundus image. We determined that it would be nearly impossible to completely automate the process relying solely on mathematical morphology. On the other hand, a potential advantage of using simpler techniques in less specialized software, with expert oversight of the final segmentations, is portability and use at other institutions for macular research.
We report a semi-automated digital method for drusen measurement in fundus photographs using commercially available software and test it for reliability against the current standard of fundus photo grading by stereo pair viewing in the central 1000-micron diameter and middle 3000-micron subfields.
Methods
Subjects
The drusen images consisted of stereo pairs of standard 35-degree film-based color fundus photographs centered on the macular regions. Clinicians expert in AMD (IB and CCWK) selected twelve good quality stereo pairs of cases with Stage 2 or 3 age-related maculopathy (as defined by the International Grading System) at random from the Columbia Macular Genetics Study (CMGS). Hence, all cases had soft drusen present but lacked the advanced lesions of geographic atrophy or choroidal neovascularization. Pigmentary abnormalities (hyper- or hypopigmentation) were not excluded. The CMGS is an ongoing cross-sectional case-control study of the possible genetic bases of macular degeneration. This study has been approved by the New York Presbyterian Hospital Institutional Review Board. One photograph from each pair was chosen for digitization. All patients were white and over 60 years of age. Photographs of normal maculae from the files of the first author (RTS) were also analyzed.
Image acquisition
All photographs were scanned and digitized (CoolScan LS-2000, Nikon Corporation, Tokyo, Japan) at resolutions of 2700 pixels/inch (actual optical resolution). The images were saved as 24-bit RGB TIFF files, with 256 levels of intensity value for each color channel.
Image Processing
For uniformity of processing, all images were resized with bicubic interpolation so that the distance from the center of the macula to the temporal disc edge was 490 pixels. These images were smaller than the originals, but still contained detail information that was more than adequate for our methods. This disc to macula distance anatomically (3000 microns) is a more reliable constant than the disc diameter (DD) often used as a clinical reference scale. We also found this approach more reliable than resizing based on camera magnifications. We worked completely within commercially available software (Photoshop 5.5, Adobe Systems Inc., San Jose, CA) on a desktop PC. The regions studied were the central 1000-micron diameter circular subfield and the 3000-micron outer diameter annular subfield (with 1000-micron inner diameter) centered on the fovea (the 1500 micron diameter anatomical center of the macula). These are the central and middle subfields defined by the Wisconsin grading template [2]. The outer 6000-micron subfield of the Wisconsin system was not used in this study.
We next corrected the large-scale variation in brightness found in most fundus photographs. The non-uniform illumination is a result of the acquisition step in the fundus photograph, and is not intrinsic to retinal reflectance. The correction process, known as shading correction, was carried out independently on each color channel, and the results combined as the red, green and blue channels of a new image. Specifically, each channel was copied, blurred (Gaussian blur, 450 μm radius), and then subtracted from the original, with constant offset values: 195 for red, 125 for green and 75 for blue. This is distinct from a difference-of-Gaussian operation that requires a much smaller kernel size for the Gaussian filter. This new average color was chosen to be a typical arbitrary extra-foveal background color, so that the result was a color-balanced shading-corrected fundus picture recognizable to the human eye. We called this the standardized image. While the offsets are mathematically arbitrary, and do not affect a study of image variation numerically, we found that human recognition of fundus features was essential. Further optimization of visual recognition of fundus features could be achieved by contrast enhancement in Photoshop (see below).
The resulting standardized images had the property that relative variation in brightness on a small scale was preserved with respect to the originals. Large-scale photographic variation as a source of bias had been removed, and the mean background colors of these images were nearly identical. Each standardized image was also stored with contrast-enhanced versions (Photoshop/Autolevels and Autocontrast) for ease of visual recognition of drusen. We found, as have others [17,18], that drusen had greater contrast in the green channel than in the other channels, or other combinations of channels. All further analysis and drusen segmentation were hence carried out on the green channel of the standardized image, with the full color contrast-enhanced versions used for subjective comparison.
Macular background leveling in images with drusen
This process takes place entirely within the Photoshop program. The semi-automated method relies on correcting the normal concentric patterns of macular reflectance [26]. These concentric elliptical patterns have the additional property that the background reflectance is radially increasing in all directions from the macular center. The ideal correction, then, would be to add back in to the image a signal with peak at the fovea and tapering radially that exactly compensated for the loss of central reflectivity in the underlying macular background pattern.
A macula interspersed with drusen, however, obstructs exact measurement of the reflectance pattern. Therefore, we have developed an approximate leveling based on the concentric elliptical geometry that "fills in" the non-background regions occupied by drusen (or other pathology). The method relies on the patches of normal to near normal retina amongst the drusen to provide a skeleton framework for what that underlying background would have been. At each step of the procedure, a prescribed elliptical region surrounding the center is brightened by an additive or multiplicative (percentage) correction; drusen included are thus brightened along with the background, so that a single threshold may ultimately identify them. If other abnormalities such as RPE hypopigmentation were present, they would be brightened also, hence possibly included in the final threshold (See Results and Discussion).
Step 1. Semi-automated method: luteal pigment correction
A major factor in these centrally darker patterns is absorbance by luteal pigment. We found in our mathematical modeling (data not presented) that fits to macular data were significantly improved when the region with evident luteal pigment was fit separately. Hence, if luteal pigment was evident (as judged by the presence of a disc of characteristic yellowish coloration in the central macula, or marked central background darkening consistent with that of luteal pigment), this region was corrected first. The corrections in this step were all multiplicative.
As an absorber, luteal pigment will reduce the brightness of each underlying structure by a percentage. We therefore constructed appropriate annular zones in the macula for percentage (multiplicative) increases in brightness to be empirically determined using published data on the spatial distribution of macular pigment [29,30]. These observers found that the macular pigment density (hence optical density) is greatest centrally, drops to half-maximum within a diameter of 500 to 600 μm, reaches a quarter-maximum at a diameter of about 1000 μm, and thence tapers slowly to a low constant level within a 2000 μm diameter region. We thus chose to bracket the 500 to 600 μm half-maximum range with a central disc of diameter 375 μm and an annulus of diameter 700 μm. We chose the next annulus of 1000 μm diameter to match the quarter-maximum density range, followed by a final annulus of 1250 μm, after which the effect of luteal pigment appeared to be essentially constant. The correction percentages to be used in these regions were determined empirically by testing on images from several subjects with clinically apparent luteal pigment. We looked at the green channel of these images (standardized as in Methods, III) and applied tapering percentage brightenings to them in the regions chosen above. We found that percentage increases in gray scale value of 3.5, 2.5, 1.5 and 1.0 percent, applied over the inner disc and three outer annuli of diameters 375, 700, 1000 and 1250 μm, respectively, provided essentially complete pattern corrections for some images, partial corrections for some images, but overcorrections (pattern reversal) in none. We therefore chose to fix these percentages and regions as a conservative (unlikely to overcorrect) luteal pigment correction if luteal pigment was present. The option to scale these percentages up or down in a given image was still available, but we chose not to exercise this option in the present study.
The resulting correction in any cross-section through the center was thus a series of step functions, which roughly approximated a Gaussian distribution A smoother approximation could have been achieved outside Photoshop, but the visual results of the current scheme were smooth to human observation.
The first step in the semi-automated method was therefore to apply the above correction to the green channel of the standardized image if luteal pigment was present. We then proceeded directly to the next step, interactive background leveling.
Step 2. Semi-automated method: interactive background leveling
Each iteration in this step is an additive correction, as will be described. This step was applied to the entire macular area, including the central luteal area. Hence, if the multiplicative Step 1 did not entirely level the background centrally, the leveling was completed additively in Step 2.
Since we were dealing with photography, not photometry, the choice of multiplicative or additive correction attempted to preserve semi-quantitative relationships of reflectance rather than absolute levels or precise numerical relationships [31]. Further, since reflectance variability was at issue, rather than absolute levels, we considered only the most variable components: the macular luteal pigment, dealt with above, the nerve fiber layer [32-35], and the RPE melanin [36]. The RPE melanin is denser in the fovea, and as such will reduce the reflectance of underlying drusen in much the same manner as the luteal pigment. However, the change in density from central to eccentric locations is not nearly so marked as that of the luteal pigment, and we did not include any further correction for this absorber.
In the case of the retinal nerve fiber layer (RNFL), we relied on the quantitative measurements of its spectral reflectance by Knighton [32]. The highest spectral reflectance is for blue light (460 nm), dropping off to perhaps 2/3 of this for green (510 nm). The reflectance spectrum has essentially the same shape at varying points along an arcuate nerve fiber bundle, but decreases almost linearly in magnitude with distance from the disc. The authors noted that this parallels the decline in thickness seen histologically [33-35], and hypothesized that the reflectance spectrum of the RNFL is proportional to its thickness. This hypothesis applied to the macular area implies that RNFL reflectance will be minimum centrally and will increase with its thickness to the arcades, which agrees with clinical observation and with our measurements of normal macular reflectance patterns [26]. Also, since the RNFL is transparent, with transmission on the order of 99% for visible light [31], its reflectance essentially adds to the apparent reflectance of underlying structures. This holds because if rN and rS are the reflectances of the RNFL and the subjacent structures, respectively, and tN is the transmission of the RNFL, then the net reflectance of the retina (both layers combined) will be:
rR = tN2 rS + rN
In this case tN is nearly unity, hence RNFL reflectance is additive to underlying structures such as drusen. For this reason, an additive correction was chosen to complete the background leveling.
The interactive steps in the additive correction proceed as follows. The user is presented with a pseudo-color topographic map, which highlights those areas in the image whose background lies between the foveal minimum and the higher levels toward the arcades. In Figure 1, the green channel is presented in gray scale. The color green is the pseudo-color representing those pixels whose value is within a given range of the foveal minimum, i.e., the lowest background sources. The user then draws on a graphic tablet (Intuos, Wacom Corp., Vancouver, WA) an ellipse chosen to be just large enough to enclose the background of the given pseudo-color (Fig 1A, magenta ellipse surrounding the green areas of low background). Non-background dark sources (e.g., pigment, retinal vessels) are ignored. The gray scale value of each pixel in the selected region (background, drusen and all else) within the ellipse is then raised two units, and the process repeated (Fig 1B,1C). Since each step is deliberately chosen to be only a partial correction, several iterations are performed on the resulting image until there are no more background sources below this threshold. This partial correction per step was chosen as a reasonable way to force a smoother result, since each iteration uses a new set of ovals with boundary discontinuities limited to two units. In our experience, these are indiscernible in the final result. A higher range of background is then tested, and again the background areas beneath this minimum are step-wise increased. The process terminates when all background has been increased to the higher levels at the arcades, which are the highest macular background levels [26].
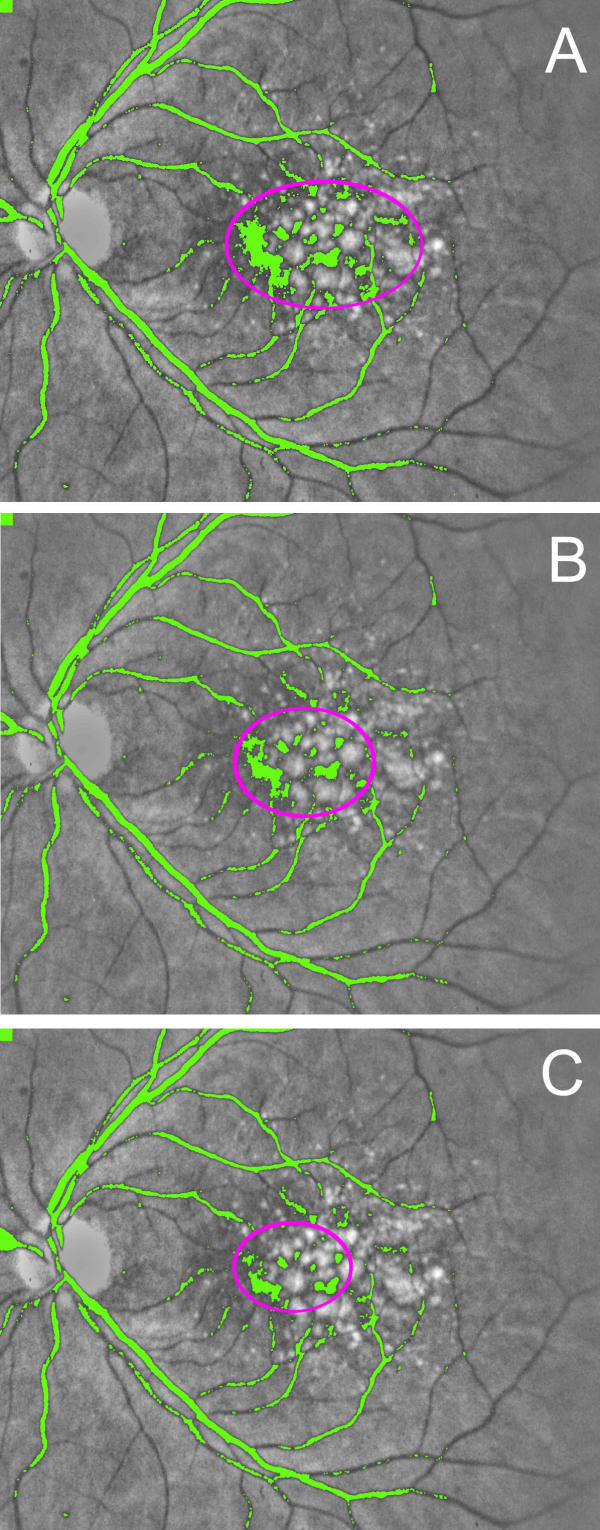
Figure 1.
Iterative macular background leveling. Processing takes place in the green channel; gray scale is used here for better reproduction. (A) All pixels darker than a fixed threshold are marked in a pseudo-color, in this case green. Note that green areas consist of the darker points in the central background, and the retinal vessels. The operator selects the size of the magenta oval such that it is just large enough to include the darker points in the central background, ignoring the retinal vessels. All pixels within this oval (both background and drusen) are brightened by 2 color intensity scale units. (B) The image created in (A) is subsequently fed back into the same algorithm. Note that all pixels darker than the same threshold are again marked in green, but the central region of darkness becomes smaller and is enclosed by a smaller magenta oval. Visualization of the retinal vessels is unaffected. The new region within the oval is further brightened as before. (C) The image created in (B) is sent back through the same algorithm. Note that the central darker region is again reduced in size, since points at the edges that were just below the threshold in (B) have been brightened. The process is continued until the macular background is uniform.
Step 3. Semi-automated method: choice of threshold
After background leveling, the optimum threshold level for drusen segmentation in the selected subfield is chosen by flicker comparison with the contrast-enhanced image, as follows. For a given threshold, the drusen image is segmented such that pixels with brightness intensities above the threshold are colored green, to label as drusen, and the rest darkened. Each such drusen image is superimposed on the contrast-enhanced image. The optimized threshold is selected by visually inspecting the correspondence of the boundaries of the segmented drusen objects to those of the contrast-enhanced objects. The threshold is then adjusted so that this visual fit is optimum in the aggregate as judged by the user. The total drusen area as a percentage of the selected subfield is then read directly (Photoshop/Histogram).
Method reproducibility and validation
Drusen area in each of the 12 digital images was measured in both the central and middle subfields by two independent graders (RTS and JKC) using the semi-automated method. Means and standard deviations were calculated. The first grader (RTS) also regraded the images in random order several weeks later, and the means and standard deviations of his gradings were calculated. An experienced retinal specialist (Grader 1, CCWK) graded the corresponding 12 stereo slide pairs independently, estimating drusen areas as a percent of the central and middle subfields in categories of 0 to 10%, 10 to 25%, 25 to 50%, and greater than 50%, as specified by the International Classification System [1]. This method of stereo pair grading is known to and accepted by clinicians as the "gold standard" for quantification of macular pathology. Another experienced retinal specialist (Grader 2, IB) also graded the corresponding 12 stereo slide pairs independently, but was asked to further refine her gold standard estimates of drusen areas as a percent of the central and middle subfields to the closest 5%. For example, if she first estimated drusen area to fall between 10 and 25%, then she was asked to assign an estimate of 10, 15, 20 or 25%. For areas less than 10%, an attempt was made to grade to the nearest 1%.
Results and Discussion
As proof of principle, we first demonstrated that the interactive procedure was effective in eliminating the concentric shading pattern in both a normal image (Figure 2A,2B,2C,2D) and a drusen-containing image (Figure 2E,2F,2G,2H). Line scans through the centers of these images (Figure 2C,2D,2G,2H) show the leveling of the central valleys in reflectance present in the originals. Since the technique raised the brightness of associated drusen along with the background, it provided a closer approximation to the underlying or true reflectance of the drusen. It was then possible to apply uniform thresholds in the central and middle subfields to define drusen boundaries (Figure 2A,2B,2C), and to create a binary image (Figure 3D) for further morphometric analysis.
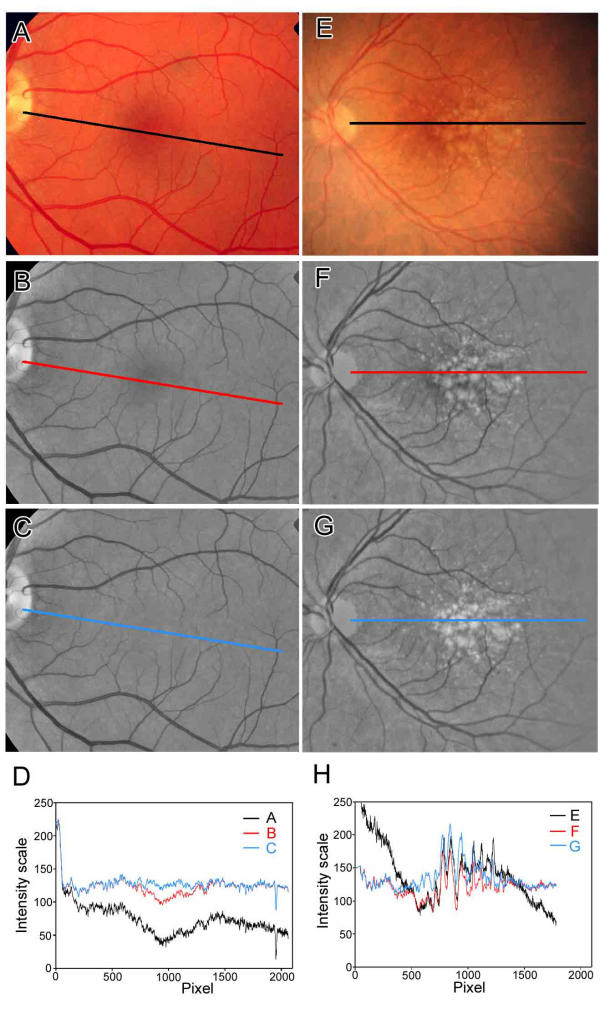
Figure 2.
Line scans demonstrating macular background leveling for drusen recognition. Left Panel. The line scans through a normal fundus image (A-D) demonstrate the effects of large-scale shading correction and macular background leveling. The color image (A) was processed and scanned in the green channel (B-D). For purposes of illustrating detail, these images were processed at higher resolution (1000 pixels from central macula to disc edge). The width of the scan line was 10 pixels. The original image (normal fundus A) is darker in the temporal quadrant and this is illustrated by the line scan (black line in D). The latter darkening is eliminated in the shading-corrected image (B) and verified by the line scan (red line in D). Note that the red line for the shade-corrected image still has a central dip of about 25 color intensity scale units corresponding to the darker central macula. This central dip is corrected with background leveling. The macular background is now quite uniform and the center is no longer dark (C). This is shown by the line scan (blue line in D). Right Panel. The line scans through a drusen-containing image (E-H) also demonstrate the effects of large-scale shading correction and macular background leveling. The color image (E) was processed and scanned in the green channel (F-H). The original image (drusen fundus E) is darker in the temporal quadrant and this is illustrated by the line scan (black line in H). The latter darkening is eliminated in the shading-corrected image (F) and verified by the line scan (red line in H). Note that the red line for the shade-corrected image (panel H, red line) still has a central dip of about 25 color intensity scale units corresponding to the darker central macula between pixels 500 and 750, but this is harder to interpret due to the multiple jagged drusen peaks. This central dip is corrected with background leveling (blue line in H). In the fundus image, the macular background between the drusen is also now uniform (G) without central darkness. Note that this technique also raises the brightness of associated drusen (G) along with the background. This is verified by the line scans, in which the drusen peaks in the central macula of the background-leveled image (blue peaks in H) are raised above the peaks in the image before background leveling (red peaks in H), allowing a uniform threshold.
Figure 3.
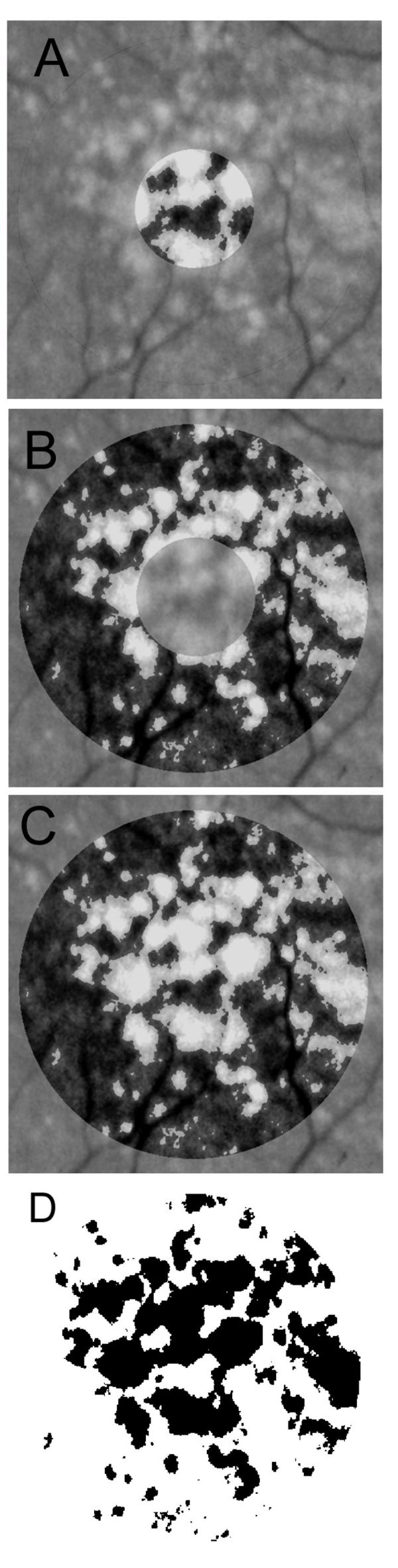
Drusen segmentation in central and middle subfields. The background-leveled drusen image from Fig 2 is shown in higher magnification. Drusen are identified by single threshold operations, respectively, in the central subfield (A), middle annular subfield (B), and combined regions (C), with the bit-mapped version (D) of segmentation (C) shown as being suitable for quantitative morphometric analysis.
Another application of this method to a drusen image is seen in Fig 4. The first frame is the standardized color image, which then was contrast-enhanced in Photoshop for ease of drusen visualization (middle frame). The last frame is the final drusen segmentation after leveling the macular background. As in Fig 3, minor errors are present, but no significant bias between quadrants or between central and middle subfields is observed. We found similar scattered errors in all images tested, but overall good qualitative agreement with the human graders.
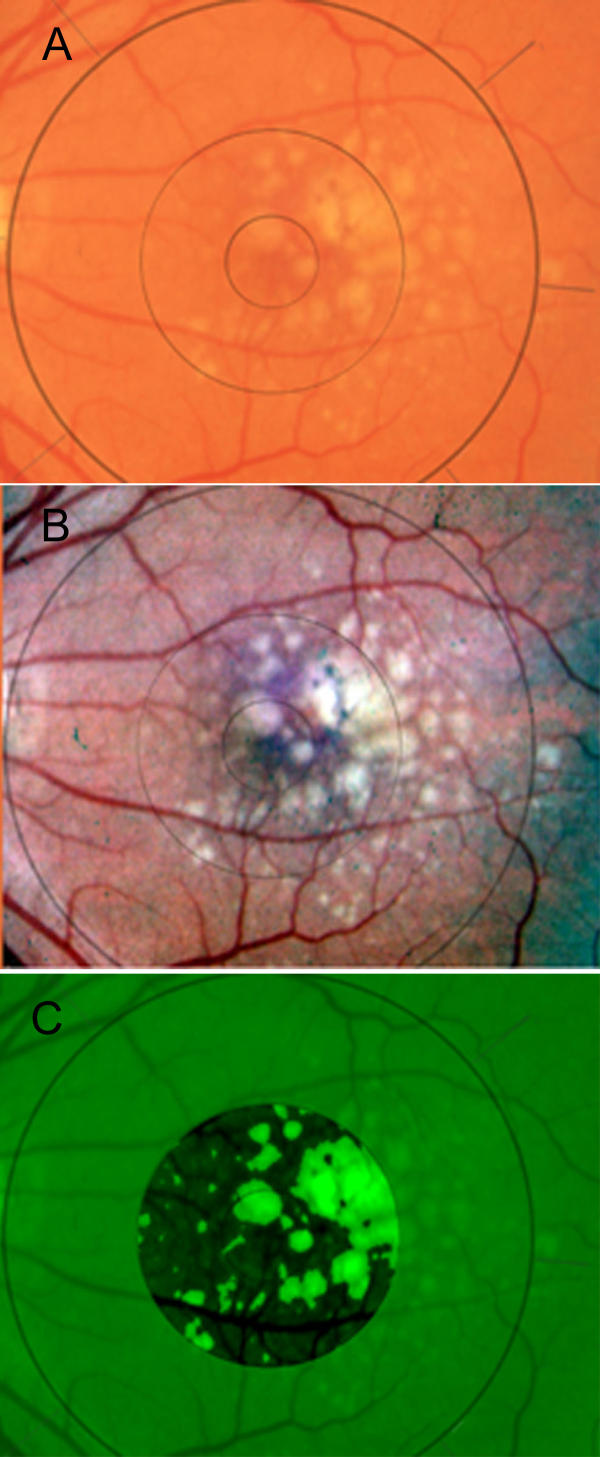
Figure 4.
Clinical case of drusen. A) Standardized color image with the inner, middle and outer regions of the Wisconsin template. Multiple large, soft drusen are present; B) the same image contrast-enhanced in Photoshop to assist in drusen identification. Note that pigment figures also stand out in this image; C) Final segmentation in the green channel after luteal correction and macular background leveling in the combined middle and central subfields, and choice of a global threshold. Close inspection shows small errors of segmentation and/or drusen boundaries with this threshold, but these are rather randomly distributed between the central and middle subfields, as well as between the four quadrants. There do not appear to be noticeable systematic errors here.
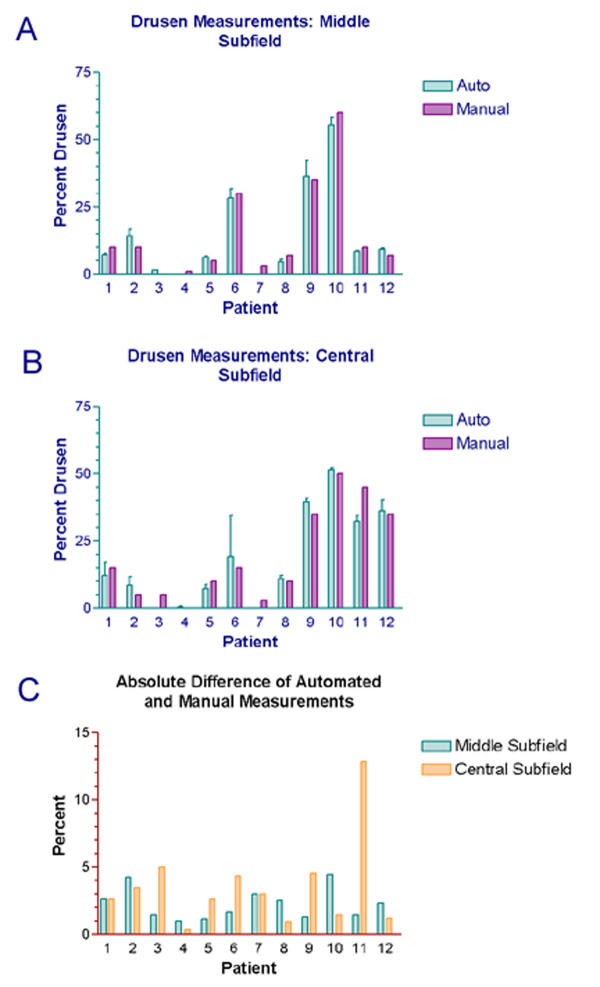
Testing of the digital method showed good inter-observer reproducibility in two independent measurements of 24 subfields (two subfields each from 12 images). The means of the two measurements had standard deviations ranging from 0.2% to 21.4%. Despite the large outlier, these standard deviations were less than 5% in 20 of 24 cases, and the median was 1.9%. This reproducibility compared favorably with that of standard methods [8]. There was one large deviation in the central subfield of Patient 6 (see Bar graph, Fig 5B). In this case, the photograph was of borderline quality due to cataract, and a large pale area within the central subfield was digitally segmented as drusen by one observer (JKC) and left out by the other observer (RTS). The clinical graders were also divided in their opinions as to whether this lesion was a druse or retinal pigment epithelium (RPE) hypopigmentation.
Figure 5.
Bar graphs: results of semi-automated vs. stereographic manual measurements. Bar graph (A) compares the measured percentage of drusen in the middle subfield obtained by two different methods. The semi-automated method uses computer-assisted interactive macular background leveling followed by a global threshold, and the manual grading estimates drusen areas from the original photographs viewed as stereo pairs (the gold standard). The means and standard deviations of independent computer-assisted measurements by two observers are displayed. The standard deviations, as shown on each bar, represent the reproducibility of the computer-assisted method. Bar graph (B) shows a similar comparison in the central subfield. Bar graph (C) displays the absolute differences between the automated measurements and the manual measurements in the central and middle subfields.
Intra-observer reproducibility of the digital method was tested by means of two temporally separated measurements by one observer. The mean measurements had a median standard deviation of 1.8% (range, 0% to 4.4%). These standard deviations were less than 5% in 22 of 24 cases. Overall, agreement was slightly better than for the inter-observer measurements, but not in every case. On review, intra-observer disagreements appeared to be more due to the subjective choice of threshold for final segmentation rather than to disparities in the final background-leveled image to which the threshold was applied.
For method validation, we then compared the results of the semi-automated digital method (24 fields from 12 slides) with the clinically accepted gold standard of expert stereo gradings of the same 24 fields from the 12 corresponding stereo pairs of slides. Comparison of the mean digital area measurements to the categories obtained by stereo Grader 1, who used the International Classification, showed 92 % agreement (22/24 digital measurements fell into the range in the International Classification chosen by Grader 1). The two disagreements were both in the middle subfield (digital measurement 41%, Grader 1 category greater than 50%; digital 7.3%, Grader I, 10 to 25%).
The mean digital area measurements were then compared to the more precise estimates of stereo Grader 2 (Bar graphs, Fig 5 and see Table 1.xls). The 95% limits of agreement [37] between the mean digital area measurements and this second set of stereo gradings were -6.4 % to +6.8 % in the central subfield and -6.0 % to +4.5 % in the middle subfield. The mean absolute differences between the digital and stereo gradings were 2.8 +/- 3.4 % in the central subfield and 2.2 +/- 2.7% in the middle subfield. Comparison with stereo grader 2 thus showed excellent agreement overall, with better agreement in the middle subfield (3000 micron diameter annulus) than in the central subfield (1000 micron diameter circle), as evidenced by the smaller absolute differences. The reason was that inclusion or exclusion of any single lesion in the smaller region had a proportionally larger effect on the measurement. With the exception of one measurement in the central subfield (Patient 11), the mean digital measurements were all within 5% of those of stereo Grader 2 (see Bar graph, Fig 5C). The measurements were often closer for those images with scanty drusen (<10%) in which Grader 2 made estimates to within 1%, but these findings were not statistically significant.
Table 1.
Semi-automated vs. stereographic manual drusen measurements. Measurements of drusen in the middle and central subfields were performed on twelve patients with AMD. Area measurements were made using the digital method by two independent graders (RTS and JKC). The means and standard deviations are displayed for the middle and central subfields. Similarly, stereo grader 2 (IB) estimated the percentage of drusen in the middle and central subfields using the original fundus photographs as stereographic pairs.
| Semi-automated drusen measurements (%) | Manual drusen measurements (%) | |||||
| ID # | Middle Subfield | std | Central Subfield | std | Middle Subfield | Central Subfield |
| 1 | 7.3350 | 0.4455 | 12.3450 | 6.4135 | 10 | 15 |
| 2 | 14.2600 | 3.3517 | 8.4750 | 4.7588 | 10 | 5 |
| 3 | 1.4550 | 0.1626 | 0.0000 | 0.0000 | 0 | 5 |
| 4 | 0.0000 | 0.0000 | 0.3400 | 0.4808 | 1 | 0 |
| 5 | 6.1600 | 0.7354 | 7.3350 | 1.9587 | 5 | 10 |
| 6 | 28.3700 | 4.8790 | 19.3550 | 21.4324 | 30 | 15 |
| 7 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 3 | 3 |
| 8 | 4.4550 | 1.5910 | 10.9500 | 1.9092 | 7 | 10 |
| 9 | 36.3100 | 8.5136 | 39.5600 | 1.7395 | 35 | 35 |
| 10 | 55.5350 | 3.7265 | 51.4350 | 1.2233 | 60 | 50 |
| 11 | 8.5500 | 0.3536 | 32.1550 | 3.3163 | 10 | 45 |
| 12 | 9.3200 | 0.5940 | 36.1850 | 5.6781 | 7 | 35 |
The above examples with larger errors illustrate the important point that both our method and the current standard of manual stereo grading are subjective, and occasional large disagreements may occur with either method. In our method, the subjective steps include: whether or not to make a luteal pigment correction; the exact placement of the ovals at each step of the interactive procedure; and the final choice of threshold for segmentation in each subfield. The manual stereo grading method is entirely subjective. Furthermore, while our procedure is logically based on a semi-quantitative geometric study of macular reflectance [26], there are photographic nonlinearities in each step that are incorporated only qualitatively. Hence, the procedure itself can be evaluated quantitatively only as to the validity of its outcome in comparison to the subjective current standard of stereo slide viewing at a light box.
A limitation of the present method is that introduction of substantial other pathologies besides drusen might confound our techniques, whereas a trained human observer makes such distinctions quickly. For example, areas of RPE hypopigmentation or frank geographic atrophy with higher reflectance in the green channel could be included in the drusen threshold. These would have to be removed manually or by additional software relying on other features. Image quality can also make the differentiation of drusen and RPE abnormalities difficult by any method. Another source of variability not encountered in this study of Caucasians could include racial pigmentation. However, we had found that the macular reflectance patterns in standardized images from normal subjects from other races were the same as those of Caucasians [26]. Hence no new difficulty would be anticipated in drusen segmentation in these populations.
Other sources of possible error in the automated method are as follows: the leveling of the macular background is an approximation that may make a given section too bright or too dim by a few units of gray scale. Drusen in such an area would be over or under-represented accordingly. Likewise, variation in the placement of the ovals in the interactive steps would lead to local irregular variability in the final leveled image. This latter error, however, tended not to be cumulative since the iterative process is to some extent self-correcting. That is, if a dark region of pixels were missed by one oval for brightening, they would still be "too dark" in the next iteration and should be picked up there. Hence, errors of this kind in the final result tend to be limited to that of a single iteration (two gray scale units). In practice, a) errors of opposing signs in different sections will tend to cancel out around the mean error, and b) the mean error will tend towards zero when the optimum threshold is chosen by the user to give the best subjective segmentation overall (i.e., if the image on average is too bright, the user will tend to use a higher threshold). This probably explains why our semi-automated results give close agreement in total area to the gold standard estimates. However, there may still be sections of an image in which the semi-automated segmentation is incorrect by wider margins. This means that if it is important to have the greatest precision in a particular subregion other than the standard subfields, a specific threshold for this region should be chosen separately. As noted above, however, we did not find any systematic errors of segmentation with respect to quadrants or subregions.
The luteal pigment correction, which was determined empirically, could similarly affect central macular drusen segmentation. Luteal pigment density of course varies in density and distribution between individuals, especially in AMD, and in this study we allowed only two options: apply the fixed correction in a given image, or not. As noted in the Methods, we used data on several normal subjects to aim deliberately for under-correction in this step, hence maintaining reflectance pattern concentricity. Further corrections could then be applied in the next steps, iterative background leveling. As it happened in this study, both observers thought that luteal pigment was present and thus applied the fixed correction in every case. As noted in the Methods, however, this correction is scalable. By the same reasoning as above, if it were desired to have the most precise segmentation of central macular drusen, the luteal correction scale could be optimized. Ideally, direct measurement of luteal pigment density by an independent method could have been incorporated. We did not pursue this here since central subfield segmentation appeared adequate.
The utility of a method is also a function of the human effort, i.e., time, required to evaluate a given image. The semi-automated method required, after training, about ten minutes of observer time (negligible computer time) per slide to complete drusen segmentation. Manual placement of ellipses followed by subjective decisions regarding final threshold choice was the most time consuming. We estimated that full automation of the background-leveling steps associated with ellipse placements, etc. would reduce operator time to about five minutes in total. Grader 2 required approximately ten minutes for the more precise gradings in two fields. Grader 1, highly experienced, needed about five minutes to grade by the International Classification System.
Conclusions
Quantification of drusen is essential to the study of age related macular degeneration. Current techniques are relatively imprecise, subjective, and labor intensive. By applying our findings with respect to macular reflectance patterns we have developed a reproducible, validated semi-automated method for leveling the macular background and segmenting drusen by a uniform threshold. At the present level of automation, this method can give drusen measurements at a higher level of precision (+/- 5%) than the widely used International Classification System, with a tradeoff of longer operator time until background leveling can be fully automated. The choice of a final threshold is still subjective, but its global application enforces some degree of objectivity as well.
Treating the macular background as a whole is a significant conceptual advance over previous methods, which rely on multiple local thresholds. Differentiation of drusen from RPE hypopigmentation, however, is still a limitation for both our method and previous methods in dealing with more complex images. The main practical advantage to our technique is that in leveling the macular background, the same correction is smoothly and simultaneously applied to the drusen embedded within the image, with the dimmer central ones being brightened or enhanced. There is still intrinsic variability in terms of the true reflectance of drusen, but the variability in background reflectance is largely eliminated. The result is increased precision and objectivity in drusen measurement.
Authors' contributions
RTS with the assistance of all the co-authors developed the digital drusen measurement method and wrote the paper.
TN contributed image analysis and software expertise in method development.
JRS provided cell biology expertise concerning the reflectors and absorbers in the macula.
IB and CCWK provided clinical expertise in method development, selected the clinical slides for testing the method and made independent drusen measurements by stereo pair grading for method validation.
JKC independently applied the digital measurement method to test reproducibility and did statistical analysis.
All authors read and approved the final manuscript.
Acknowledgments
Acknowledgements
The authors wish to thank Prof. Robert Knighton for reviewing an earlier version of the manuscript.
Contributor Information
R Theodore Smith, Email: rts1@columbia.edu.
Takayuki Nagasaki, Email: tn4@columbia.edu.
Janet R Sparrow, Email: jrs88@columbia.edu.
Irene Barbazetto, Email: ib206@columbia.edu.
Caroline CW Klaver, Email: carolineklaver@yahoo.com.
Jackie K Chan, Email: jc804@columbia.edu.
References
- Bird AC, Bressler NM, Bressler SB, Chisholm IH, Coscas G, Davis MD, de Jong PT, Klaver CC, Klein BE, Klein R. An international classification and grading system for age-related maculopathy and age-related macular degeneration. Survey Ophthalmol. 1995;39:367–374. doi: 10.1016/s0039-6257(05)80092-x. [DOI] [PubMed] [Google Scholar]
- Klein R, Davis MD, Magli YL, Segal P, Klein BE, Hubbard L. The Wisconsin age-related maculopathy grading system. Ophthalmology. 1991;98:1128–1134. doi: 10.1016/s0161-6420(91)32186-9. [DOI] [PubMed] [Google Scholar]
- Klaver CC, Wolfs RC, Vingerling JR, Hofman A, de Jong PT. Age-specific prevalence and causes of blindness and visual impairment in an older population: the Rotterdam Study. Arch Ophthalmol. 1998;116:653–658. doi: 10.1001/archopht.116.5.653. [DOI] [PubMed] [Google Scholar]
- Smiddy WE, Fine SL. Prognosis of patients with bilateral macular drusen. Ophthalmology. 1984;91:271–277. doi: 10.1016/s0161-6420(84)34309-3. [DOI] [PubMed] [Google Scholar]
- Bressler SB, Maguire MG, Bressler NM, Fine SL. Relationship of drusen and abnormalities of the retinal pigment epithelium to the prognosis of neovascular macular degeneration. The Macular Photocoagulation Study Group. Arch Ophthalmol. 1990;108:1442–1447. doi: 10.1001/archopht.1990.01070120090035. [DOI] [PubMed] [Google Scholar]
- Bressler NM, Bressler SB, Seddon JM, Gragoudas ES, Jacobson LP. Drusen characteristics in patients with exudative versus non-exudative age-related macular degeneration. Retina. 1988;8:109–114. doi: 10.1016/0278-4327(88)90022-3. [DOI] [PubMed] [Google Scholar]
- Holz FG, Wolfensberger TJ, Piguet B, Gross-Jendroska M, Wells JA, Minassian DC, Chisholm IH, Bird AC. Bilateral macular drusen in age-related macular degeneration. Prognosis and risk factors. Ophthalmology. 1994;101:1522–1528. doi: 10.1016/s0161-6420(94)31139-0. [DOI] [PubMed] [Google Scholar]
- Abdelsalam A, Del Priore L, Zarbin MA. Drusen in age-related macular degeneration: pathogenesis, natural course, and laser photocoagulation-induced regression. Survey Ophthalmol. 1999;44:1–29. doi: 10.1016/S0039-6257(99)00072-7. [DOI] [PubMed] [Google Scholar]
- Little HL, Showman JM, Brown BW. effect of laser photocoagulation of confluent soft macular drusen. Ophthalmology. 1997;104:623–631. doi: 10.1016/s0161-6420(97)30261-9. [DOI] [PubMed] [Google Scholar]
- Frennesson IC, Nilsson SE. Effects of argon (green) laser treatment of soft drusen in early age-related maculopathy: a 6 month prospective study. Br J Ophthalmol. 1995;79:905–909. doi: 10.1136/bjo.79.10.905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bressler NM, Munoz B, Maguire MG, Vitale SE, Schein OD, Taylor HR, West SK. Five-year incidence and disappearance of drusen and retinal pigment epithelial abnormalities. Waterman study. Arch Ophthalmol. 1995;113:301–308. doi: 10.1001/archopht.1995.01100030055022. [DOI] [PubMed] [Google Scholar]
- Bressler SB, Bressler NM, Seddon JM, Gragoudas ES, Jacobson LP. Interobserver and intraobserver reliability in the clinical classification of drusen. Retina. 1988;8:102–108. doi: 10.1097/00006982-198808020-00004. [DOI] [PubMed] [Google Scholar]
- Figueroa MS, Regueras A, Bertrand J. Laser photocoagulation to treat macular soft drusen in age-related macular degeneration. Retina. 1994;14:391–396. doi: 10.1097/00006982-199414050-00001. [DOI] [PubMed] [Google Scholar]
- Figueroa MS, Regueras A, Bertrand J, Aparicio MJ, Manrique MG. Laser photocoagulation for macular soft drusen. Updated results. Retina. 1997;17:378–384. doi: 10.1097/00006982-199709000-00004. [DOI] [PubMed] [Google Scholar]
- Sigelman J. Macular drusen resorption one year after perimacular laser photocoagulation. Ophthalmology. 1991;98:1379–1383. doi: 10.1016/s0161-6420(91)32122-5. [DOI] [PubMed] [Google Scholar]
- The Choroidal Neovascularization Prevention Trial Research Group. Laser treatment in eyes with large drusen. Short-term effects seen in a pilot randomized clinical trial. Ophthalmology. 1998;105:11–23. [PubMed] [Google Scholar]
- Shin DS, Javornik NB, Berger JW. Computer-assisted, interactive fundus image processing for macular drusen quantitation. Ophthalmology. 1999;106:1119–1125. doi: 10.1016/S0161-6420(99)90257-9. [DOI] [PubMed] [Google Scholar]
- Rapantzikos K, Zervakis M, Balas K. Detection and segmentation of drusen deposits on human retina: Potential in the diagnosis of age-related macular degeneration. Med Image Analysis. 2003;7:95–108. doi: 10.1016/S1361-8415(02)00093-2. [DOI] [PubMed] [Google Scholar]
- Leistritz L, Schweitzer D. Automated detection and quantification of exudates in retinal images. SPIE. 1994;2298:690–696. [Google Scholar]
- Schweitzer D, Kalve B, Leistritz L, Wagner M, Hammer M. Experimental results with a wavelength-tunable scanning laser. Lasers and Light. 1998;8:143–152. [Google Scholar]
- Sebag M, Peli E, Lahav M. Image analysis of changes in drusen area. Acta Ophthalmol. 1991;69:603–610. doi: 10.1111/j.1755-3768.1991.tb04847.x. [DOI] [PubMed] [Google Scholar]
- Morgan WH, Cooper RL, Constable IJ, Eikelboom RH. Automated extraction and quantification of macular drusen from fundal photographs. Aus New Zeal J Ophthalmol. 1994;22:7–12. doi: 10.1111/j.1442-9071.1994.tb01688.x. [DOI] [PubMed] [Google Scholar]
- Kirkpatrick JN, Spencer T, Manivannan A, Sharp PF, Forrester JV. Quantitative image analysis of macular drusen from fundus photographs and scanning laser ophthalmoscope images. Eye. 1995;9:48–55. doi: 10.1038/eye.1995.7. [DOI] [PubMed] [Google Scholar]
- Goldbaum MH, Katz NP, Nelson MR, Haff LR. The discrimination of similarly colored objects in computer images of the ocular fundus. Invest Ophthalmol Vis Sci. 1990;31:617–623. [PubMed] [Google Scholar]
- Peli E, Lahav M. Drusen measurement from fundus photographs using computer image analysis. Ophthalmology. 1986;93:1575–1580. doi: 10.1016/s0161-6420(86)33524-3. [DOI] [PubMed] [Google Scholar]
- Smith RT, Nagasaki TJ, Sparrow T, Koniarek J. The Fine Structure of Macular Images [abstract] Invest Ophthalmol Vis Sci. 2001;42:153. [Google Scholar]
- Smith RT, Barbazetto I, Barile G, Allikmets R. A Digital Reading Center for Fundus Photographs of the Columbia Macular Genetics Study [abstract] Invest Ophthalmol Vis Sci. 2002;43:E-Abstract 2507. http://www.iovs.org [Google Scholar]
- Russ JC. Correcting image defects. In: Fourth, editor. The image processing handbook. Boca Raton, CRC Press; 2002. pp. 131–206. [Google Scholar]
- Bone RA, Landrum JT, Cains A. Optical density spectra of the macular pigment in vivo and in vitro. Vision Res. 1992;32:105–110. doi: 10.1016/0042-6989(92)90118-3. [DOI] [PubMed] [Google Scholar]
- Snodderly DM, Auran JD, Delori FC. The macular pigment. II. Spatial distribution in primate retinas. Invest Ophthalmol Vis Sci. 1984;25:674–685. [PubMed] [Google Scholar]
- van de Kraats J, Berendschot TT, van Norren D. The pathways of light measured in fundus reflectometry. Vision Res. 1996;36:2229–2247. doi: 10.1016/0042-6989(96)00001-6. [DOI] [PubMed] [Google Scholar]
- Knighton RW, Jacobson SG, Kemp CM. The spectral reflectance of the nerve fiber layer of the macaque retina. Invest Ophthalmol Vis Sci. 1989;30:2392–2402. [PubMed] [Google Scholar]
- Ogden TE. Nerve fiber layer of the primate retina: thickness and glial content. Vision Res. 1983;23:581–587. doi: 10.1016/0042-6989(83)90063-9. [DOI] [PubMed] [Google Scholar]
- Ogden TE. Nerve fiber layer of the primate retina: morphometric analysis. Invest Ophthalmol Vis Sci. 1984;25:19–29. [PubMed] [Google Scholar]
- Radius RL. Thickness of the retinal nerve fiber layer in primate eyes. Arch Ophthalmol. 1980;98:1625–1629. doi: 10.1001/archopht.1980.01020040477018. [DOI] [PubMed] [Google Scholar]
- Weiter JJ, Delori FC, Wing GL, Fitch KA. Retinal pigment epithelial lipofuscin and melanin and choroidal melanin in human eyes. Invest Ophthalmol Vis Sci. 1986;27:145–152. [PubMed] [Google Scholar]
- Bland JM, Altman DG. Measuring agreement in method comparison studies. Stat Methods Med Res. 1999;8:135–160. doi: 10.1191/096228099673819272. [DOI] [PubMed] [Google Scholar]