Surface molecular view of colloidal gelation

Abstract

We investigate the phase behavior of surface-functionalized silica colloids at both the molecular and macroscopic levels. This investigation allows us to relate collective properties such as aggregation, gelation, and aging directly to molecular interfacial behavior. By using surface-specific vibrational spectroscopy, we reveal dramatic changes in the conformation of alkyl chains terminating submicrometer silica particles. In fluid suspension at high temperatures, the interfacial molecules are in a liquid-like state of conformational disorder. As the temperature is lowered, the onset of gelation is identified by macroscopic phenomena, including changes in turbidity, heat release, and diverging viscosity. At the molecular level, the onset of this transition coincides with straightening of the carbon–carbon backbones of the interfacial molecules. In later stages, their intermolecular crystalline packing improves. It is the increased density of this ordered boundary layer that increases the van der Waals attraction between particles, causing the colloidal gas to aggregate. The approach presented here can provide insights into phase transitions that occur through surface modifications in a variety of colloidal systems.

Colloidal dispersions are stable because intimate contact between the dispersed particles is physically barred. Given that the particles remain independent, they can exist in distinct states of aggregation analogous to the phases of molecular matter as follows: isolated as gas particles, condensed as an amorphous liquid, or ordered as a crystal. The macroscopic phase of a colloidal dispersion expresses the balance between interparticle attraction at relatively large separations, interparticle repulsion on close contact, and the energy available as thermal fluctuations. Because of their composite nature, such mixtures offer a unique opportunity to manipulate the interparticle potential energy: Attractive forces can be screened more or less by the dielectric properties of the solvent, and repulsive forces depend on the chosen chemical modification of the particle surface. In addition to their interest as models of phase behavior, surface-functionalized colloids are increasingly used to probe biomolecular interactions (1–3), specifically at (model) membranes (4). In such cases, the extreme sensitivity of a colloidal phase to surface modification can be exploited as a detection method, with dramatic changes in the collective properties (such as phase separation and gelation) indicating, for example, molecular adsorption at the interface.

Robust dispersions can be created by attaching a bulky molecular layer to the outer surface of the dispersed particles. Such coatings resist the interparticle van der Waals attraction at close range and prohibit or delay irreversible coalescence (5). Particles that have been sterically stabilized in this way show a rich variety of phase behavior in response to external conditions (6, 7), behavior that is usually attributed to changes in the structure or order of the stabilizing molecules and their interactions with the solvent.

In particular, dispersions that are stabilized by means of terminally bound alkyl chains are known to form gels at low temperature (being reversible, this gelation is distinct from the ultimate “collapse” or coalescence of an aged gel to a noncolloidal state). The gel state has been explained variously as a consequence of percolation (8), a dynamic instability (9), a frustrated gas–solid transition (10), and a manifestation of solvent–interface interactions (11). The origin of this controversy may be traced to the prevailing indirect or incomplete knowledge of interfacial structure (6). To date, colloids have been studied by techniques that are not specifically sensitive to the surface, such as calorimetry (see ref. 12 and references therein), linear scattering of neutrons (13), x-rays and visible photons (14–21), and particle distribution imaging (4, 22).

The recent extension of nonlinear optical techniques to probe specifically the surface of (sub-)micrometer-sized particles in a scattering geometry (23–27) has enabled the detailed observation of molecular events at particle surfaces. Here, we investigate the gelation transition of alkyl-coated colloids by using the surface-specific vibrational technique of sum-frequency generation (SFG) scattering (28, 29). SFG scattering allows us to probe the conformational and orientational order of surface molecules through their vibrational modes. When we combine them with turbidity and calorimetry measurements, we can correlate the molecular interfacial properties with the macroscopic, collective, mechanical state of the colloidal dispersion. We find that the transition between macroscopic states is triggered by an order/disorder transition among molecules at the colloidal interface. The results presented here for the well documented model system of alkyl-coated colloids in n-alkane solution demonstrate the capability of this approach in unraveling the molecular basis of macroscopic colloidal transitions and should be applicable to a much wider range of surface-functionalized colloids.

Results and Discussion

Interpretation of the SFG Spectra.

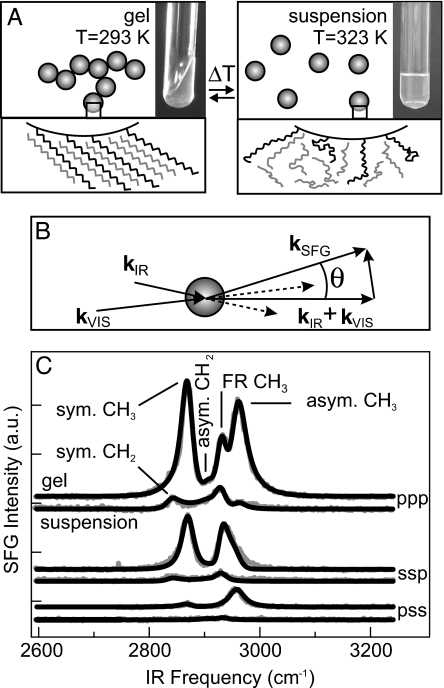
The samples consist of monodisperse silica particles with stearyl chains (C₁₈) chemically grafted to their surface (30, 31). The surface bond is a Si–O–C moiety, resulting from a condensation reaction between surface silanol groups and stearyl alcohol at 473 K. Particles of radii 123 and 36 nm were dispersed in deuterated n-hexadecane. With increasing temperature, these dispersions transform from a highly viscous gel to a freely flowing fluid, as illustrated in Fig. 1A. The transition is fully reversible (12, 32).

Fig. 1.

Overview of the experiment and key experimental results. (A) Schematic illustration of the reversible transformation from gel into suspension. The molecular-scale structural changes observed in this study are depicted with photographs illustrating the macroscopic change in viscosity. (B) The scattering geometry. k_SFG, k_VIS, and k_IR are the wave vectors of the scattered sum frequency and the VIS and IR fields; q is the scattering wave vector; and θ is the scattering angle. The detector and k vectors lie in one plane. The IR, VIS, and SFG fields are polarized either parallel (p) or perpendicular (s) to the plane of incidence. (C) Three sets of SFG scattering spectra (gray lines), obtained at three different polarization combinations. In each set the upper trace represents a gel (T = 293 K, 1 day after preparation), and the lower trace is a fluid suspension of colloidal particles in deuterated n-hexadecane-d₃₄ (T = 323 K). The three-letter codes denote the polarization states of the SFG, VIS, and IR beams, respectively. Spectra for sps (data not shown) and pss combinations are identical. The spectra were collected at θ = 51° and are offset for clarity. The black lines are fits described in the text. The vibrational modes that appear in the SFG spectra are marked in the upper pair of traces.

Fig. 1B schematically depicts the optical experiment, in which infrared (IR) and visible (VIS) laser pulses overlap within the colloidal dispersion. These electromagnetic fields drive an oscillating polarization throughout the material, but only where the sample is not centrosymmetric can this polarization have a component at the sum of the laser frequencies. Thus, sum-frequency emission is generated primarily at interfaces. For systems with macroscopic inversion symmetry, such as the colloidal dispersion investigated here, the emitted sum-frequency light has a broad angular distribution (28, 29). Although weak, it is easily separated from scattered incident laser light because of the large frequency difference. Furthermore, the SFG mixing process is strongly enhanced by molecular resonances, such as the C–H stretch vibration. By plotting the SFG intensity as a function of the IR laser spectrum, a vibrational spectrum of the molecular moieties at the surface of the colloids is obtained. Three sets of spectra are shown in Fig. 1C for different polarization combinations of the SFG, VIS, and IR light, as indicated in the plot for gel and fluid suspension states.

The CH₂ and CH₃ stretching modes of straight-chain alkyl chains are well documented and can be incorporated into the formalism describing the sum-frequency field (33, 34). The SFG spectra reflect the properties of the macroscopic nonlinear susceptibility, which is determined by molecular electronic properties (hyperpolarizability) and collective geometric ones (molecular conformational and orientational distributions of the surface alkyl chains) (33–35). Therefore, an SFG spectrum is sensitive to the degree of molecular order and orientation at the interface, in contrast to a linear IR absorption spectrum. Among the CH₂ groups, for example, local inversion symmetry is found in a highly ordered, all-trans alkyl chain, or when the chain is fully disordered, cases in which the radiated SFG intensity is very small. In intermediate cases, the SFG spectrum depends on the degree of order. Following the procedure described in ref. 28, our spectra can be reproduced by an SFG scattering model that allows the state of order to be quantified (33, 34). These model calculations are the black lines in Fig. 1C, with the underlying C–H stretching modes labeled.

From Fig. 1C, it is immediately apparent that the gel spectra are dominated by the symmetric and asymmetric methyl (CH₃) stretching modes (at 2,888 and 2,978 cm⁻¹, respectively) and that methylene (CH₂) modes (at 2,854 and 2,925 cm⁻¹) are essentially absent. Spectra of the fluid state (323 K), in contrast, contain only weak CH₂ stretch modes (plus a CH₃ Fermi resonance), whereas the CH₃ stretch modes are now below the detection limit. The overall weakness of the high-temperature spectrum is interpreted as a consequence of liquid-like disorder in a melted monolayer: The orientational distribution of terminal methyl groups is effectively isotropic (hence, no signal), but among the methylene groups a bias persists with respect to the particle surface, a consequence of their being chemically anchored to it (see, e.g., ref. 36). In the gel phase (293 K), these weak methylene signals vanish, an indication of the higher degree of centrosymmetry that is present within a crystalline slab of alkyl chains. In addition, for the gel, the dominant methyl signals are characteristic of a well ordered outer terminal layer of methyl groups. In other words: there are very few packing defects in the boundary layer, and the methyl groups are highly oriented with respect to the surface (35, 37).

The ordered and disordered boundary-layer scenarios are sketched in Fig. 1A. Here, surface-bound stearyl chains are shown mingling with the deuterated n-hexadecane solvent. This behavior is to be expected in the molten-monolayer phase, but intercalation in the highly ordered crystalline phase can be deduced from the spectroscopic results as follows. An analysis of the SFG spectra provides the tilt angle of the methyl groups and thus the characteristic tilt of the straight stearyl chains with respect to the local surface plane. In the gel phase, an angle of 52 ± 5° is obtained. Alkane crystals pack, by definition, at their van der Waals contact distance. This packing is routinely observed in self-assembled crystalline monolayers, which tilt precisely until the alkyl chain crystal density is achieved (38). In the present case, we estimate (from a comparison with self-assembled monolayers of known density; data not shown) that the coverage of stearyl groups is ≈1 per nm² (corresponding to ≈30–60% coverage). For the fully ordered layer, this coverage requires filling with >40% hexadecane molecules to achieve the crystalline density. This number is corroborated by experiments in which 20% of the solvent was not deuterated. A marked decrease in SFG signal intensity was observed because of destructive interference between the vibrations of the solvent and surface alkyl chains (39).

Correlation of SFG Response with the State of Gelation.

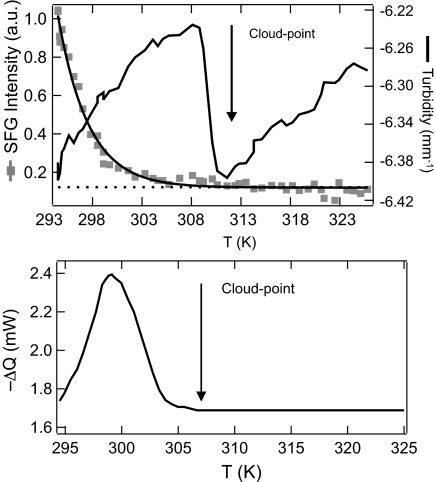
The gelation transition is named for its most conspicuous manifestation: the very high viscosity resulting from colloidal aggregation. To document the extent of colloidal aggregation, however, a nonmechanical probe is preferable. One such measure is elastic light scattering, expressed as turbidity. This visible cloudiness is greatest when aggregates of colloidal particles have structural features on a length scale comparable with the wavelength of visible light. The variety of SFG spectra discussed earlier can also be summarized in a single numeric index by integrating the entire C–H stretching spectrum. Fig. 2Upper shows this integrated SFG intensity together with the turbidity as a function of temperature. The turbidity shows a minimum at 310 K (known as the cloud point). The cloud point marks the transition between a stable uniform suspension at higher temperatures and an unstable region at lower temperatures in which heterogeneous and strongly scattering aggregates are present. In the latter region, the integrated SFG intensity decreases by an order of magnitude as the gel is heated from 293 K up to the cloud point at 310 K. Therefore, the qualitative change from an ordered to a disordered boundary layer occurs in the same temperature range as the physical breakup of an aggregated gel. Fig. 2 Lower shows that this temperature range is also a region of thermodynamic significance. Here the calorimetric excess thermal power (compared with neat hexadecane) is plotted as a function of increasing temperature. During breakup, the latent heat of gelation is evidently absorbed in a range of temperatures ≈15 K below the cloud point. This measurement was performed on a colloid chemically identical to that used for optical measurements but consisting of smaller particles. Their larger effective surface area yields a larger calorimetric signal. The latent heat is exclusively due to changes in the surface state of the colloids and not due to the colloidal transition itself. This conclusion is apparent from two independent observations: There is no excess heat of gelation when the surface transition does not occur (in a different solvent; data not shown), and the latent heat scales with particle surface area (39).

Fig. 2.

Nonlinear and linear optical response and thermodynamic behavior of the colloidal suspension vs. temperature. (Upper) Spectrally integrated SFG intensity and turbidity as a function of temperature for 123-nm particles. The line representing a single exponential decay is to guide the eye. (Lower) Calorimetric excess heat flow from a 28.9 vol% dispersion of 36-nm particles in deuterated n-hexadecane (≈30 min after preparation). The onset of aggregation is marked with an arrow in both images.

In light of the results presented in Fig. 2, we can consolidate our description of the gel breakup process and relate the surface molecular changes to those observed on the macroscopic level. As the temperature increases toward the cloud point, heat is absorbed by the initially crystalline interface and drives a molecular phase transition to a fluid state (40). A consequence of this transition is less efficient packing of molecules and hence a decrease in the density of the colloidal boundary layer. It has been shown that density changes of this magnitude (liquid vs. crystalline alkyl chains) can substantially modify the van der Waals interaction potential between colloidal particles (41, 42). This modified interaction potential results in a colloidal phase transition to a disaggregated, colloidal gas state. No change in the number of grafted chains is required; the average mass density may change through variations in the alkyl chain packing.

The present SFG measurement is not directly sensitive to the solvent molecules. Additional order/disorder phenomena may occur in the hexadecane that is adjacent to the boundary layer, perhaps contributing to the colloidal thermodynamics. It is convenient to separate such effects according to whether they occur globally or only at the contact points. Regarding the first possibility, there are well documented examples of a crystalline alkane monolayer inducing order in the closest layer of a contacting liquid (43). Interfacial freezing can also be spontaneous in the presence of surfactants, for example, at the tetradecane-water boundary (44). Such ordered solvation shells would obviously contribute to the colloidal phase behavior. Alternatively, solvent that is trapped in the region of close contact between two particles may become ordered or aligned purely because of confinement (45). Insofar as this process is a pressure-induced crystallization, it can lead to an effective attraction between particles. In this section we have given evidence that the boundary-layer phase transition is the primary driving force; but because the solvent is already implicated in this transition, and secondary ordering phenomena may be expected, the detailed role and structure of the solvent is not yet known.

Orientation and Alignment During Gel Aging.

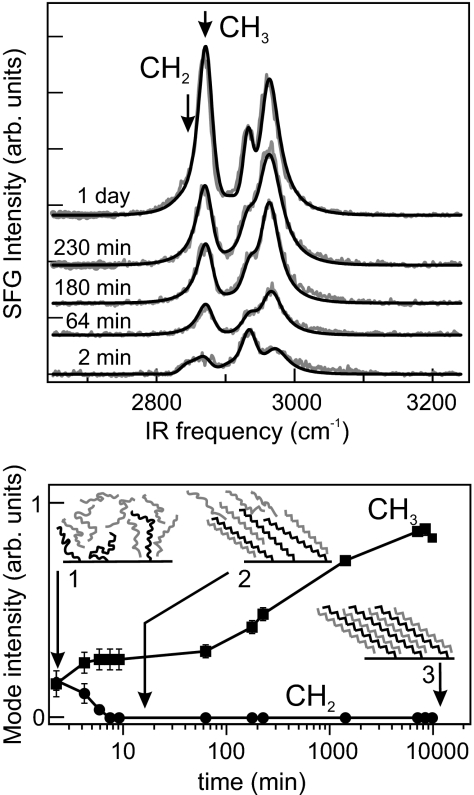
Although the integrated SFG intensity serves as a useful index of interfacial crystallinity, the spectra themselves can be analyzed in greater detail to reveal changes in the surface molecular organization. This analysis is particularly insightful for the reverse of gel breakup, namely, gelation triggered by crystallization of the boundary layer. Fig. 3Upper shows SFG spectra several times after rapidly cooling a freshly prepared dispersion. The first spectrum is weak; its strongest component (2,952 cm⁻¹) is in a region of unreliable Fermi resonances, but the CH₂ symmetric stretch is also present (2,854 cm⁻¹). Within a few minutes, the CH₃ modes appear. It is on this timescale that the sample ceases to flow under its own weight. Fig. 3 Lower displays the amplitudes (obtained from the fits) of the symmetric CH₃ and CH₂ stretching modes. A geometrical analysis of how their relative intensities are affected by the transition dipole distributions can be used to measure the orientational and conformational order in the surface layer (35, 36, 46–48). These traces show that upon gelation the CH₂ stretch mode quickly falls below the detection limit. Qualitatively, this result indicates that after ≈7 min, the SFG-active chain defects have already disappeared, and the interfacial alkyl chains are in the straight, all-trans conformation. At this stage, the dispersion is already gelatinous. However, the CH₃ signal continues to increase for several days after the formation of the gel. This result means that in addition to the fast molecular stretching process, there is a slow, collective alignment of the surface chains. SFG is particularly sensitive to such rearrangement because the individual molecular vibrational amplitudes add coherently to yield a bulk signal. The observation of very slow annealing of the surface layer is consistent with calorimetric measurements: The amount of heat required to break up a 3-day-old gel is 8% greater than that for a freshly prepared gel (data not shown). Three distinct surface states can be distinguished in the gelation process, as schematically depicted in Fig. 3 Lower. Initially, the molecular conformation and orientation of the surface groups are highly disordered. Over the course of minutes, the surface-anchored alkyl chains straighten out and assume the so-called all-trans configuration. Although the conformations are now uniform, orientational order is not yet present. The collective orientation of the ensemble of surface molecules occurs on timescales that are larger by ≈2 orders of magnitude. This slow relaxation process is not caused by lateral diffusion of surface-bound stearyl groups or changes in their coverage (through adsorption or desorption), because the covalent Si–O–C surface bond is too strong.

Fig. 3.

Temporal evolution of the colloidal surface after gelation. (Upper) SFG spectra (gray lines, ppp polarization) of a 24 vol% gel as a function of gel age as indicated. Fits (black lines) were performed as described in ref. 28. (Lower) Amplitude of the symmetric CH₃ (squares) and CH₂ (circles) stretch modes at the frequencies indicated by the arrows in Upper. The structure of the boundary layer is schematically depicted for the three most relevant time intervals during gel formation and aging.

The observed fast stretching and slow reorientation in the surface film have been reported for self-assembled monolayers (SAMs) of docosanethiol [CH₃(CH₂)₂₁SH] on polycrystalline gold (e.g., ref. 49). In the first few minutes after formation of the SAM, the chain defects disappear, followed by a gradual in-growth of the CH₃ stretch vibrations. This slow but large rise was assigned to a slight reorientation of the alkyl chains as the layer becomes fully packed. The final densification is driven by the last few percent of thiol headgroups adsorbing onto the gold surface. In the present case, stearyl monolayers on silica behave similarly with the final densification being due to the interdigitation of solvent molecules into the alkyl monolayer. Indeed, the increase of the CH₃ stretch mode intensity with time can be fully accounted for by a decrease in the distribution of the C–C backbone tilt angle from 25° to 8°. An average tilt of 52 ± 5° from the local surface normal has been calculated from SFG spectra at different polarization combinations (33). This increase in order can be accounted for by insertion of solvent molecules between the surface bound chains (as illustrated in Fig. 3). Although one would expect the interdigitation to give rise to a slight change not only in the distribution of tilt angles, but also to an increase in the average angle itself, this effect is estimated to be within the experimental error. Other annealing mechanisms that may enhance the methyl SFG signal are alignment in response to shear and the coalescence of rotational domains.

This densification of the surface layer has consequences for the interparticle colloidal interaction: It has been shown that a density increase of ≈1% deepens the interaction potential between micelles of ≈5-nm radius from −1.58 to −5.51 kT (42). Thus, the density increase reflected in the SFG spectra leads to an increase in the van der Waals interaction, as will the slow orientational relaxation accompanying the annealing process. Although our data do not provide direct evidence for such a mechanism, it was shown in ref. 50 that for coated spheres in contact it is the van der Waals interactions between the shells that gives the most important contribution to the total attractive interactions. Moreover, for short distances the van der Waals interactions scale with the radius of the sphere (or shell). Therefore, if such interactions can be significant for micelles as small as 5 nm, they can certainly be important for particles several times that size. During gel aging, additional ordering of the alkyl chains occurs, and the particle–particle attraction therefore becomes stronger, which should increase the frictional resistance to particle–particle reorientation. It follows that the particle–particle reorientations that constitute the aging process (leading ultimately to collapse) slow down with time (18–21, 51).

Conclusions

We have obtained a clear picture of the role molecular order plays on the phase behavior of a colloidal dispersion. In combination with turbidometry and calorimetry, vibrational sum-frequency scattering provides the direct connection between the molecular interfacial properties and the collective colloidal properties. These results illustrate the subtle interplay between surface groups and solvent molecules in determining the particle–particle interaction potential. On planar surfaces, vibrational SFG has been successfully used to identify molecular changes resulting from variations in temperature, charge, and pressure (see, e.g., refs. 52 and 53). Therefore, we expect that the method presented here will be applicable to other cases of bulk colloidal behavior that is mediated or triggered by a change of interfacial molecular structure.

Materials and Methods

The samples consist of stearyl alcohol (C₁₈H₃₇OH)-coated (30) silica particles (31) with radii (σ) of 123 and 36 nm dispersed in n-hexadecane-d₃₄ (Aldrich, St. Louis, MO; 98 atom % D, deuterated to suppress absorption of the IR light by the solvent) with a colloid volume fraction of 24%. Gels were prepared in a 1-mm path-length cuvette (Hellma GmbH, Müllheim, Germany) by dispersing the particles in warm (≈323 K) solvent and cooling the resultant dispersion to room temperature. If small gas bubbles (≈0.1 mm) did not rise through the dispersion, it was classified as a gel. The angle of maximum scattered intensity (measured in air) was 51°. For temperature-dependent turbidity and sum-frequency scattering measurements, the sample temperature was raised at a rate of 2.9 K/min by resistively heating the sample holder. Calorimetric measurements were performed at a heating rate of 0.5 K/min on a differential scanning calorimeter (DSC III; Setaram, Caluire, France) with a detection limit of 0.2 J/g.

The SFG experiments were performed by using a broadband, multiplex scheme operating at 1 kHz similar to that described in refs. 54 and 55. The IR laser spectrum was centered at 2,900 cm⁻¹ with a bandwidth of ≈180 cm⁻¹ (FWHM). Individual pulse duration was 120 fs with a typical energy of 7 μJ. The VIS laser spectrum was centered at 800 nm, and its 7-cm⁻¹ bandwidth (FWHM) determined the sum-frequency spectral resolution. The selectively polarized IR and VIS pulses were incident under a relative angle of 15° and focused down to an ≈0.4-mm beam waist. The scattered SFG light was collimated with a lens (with an angular acceptance of 17°), polarization selected, and dispersed by a spectrometer onto an intensified CCD camera. In the procedure to determine the molecular orientation, intensity variations due to polarization-dependent IR and VIS intensities and detector efficiency were taken into account. The acquisition time for one SFG spectrum was typically 100 s.

Turbidity measurements were performed with a 5-mW HeNe laser and detected with a CCD camera (Roper Scientific, Trenton, NJ). The sample scattering strength was determined through the decrease in the intensity of the forward beam.

Abbreviations

SFG

sum-frequency generation

VIS

visible.