Robust Temporal Coding in the Trigeminal System

Abstract

The ability of rats to use their whiskers for fine tactile discrimination rivals that of humans using their fingertips. Rats perform discriminations rapidly and accurately while palpating the environment with their whiskers. This suggests that whisker deflections produce a robust and reliable neural code. Whisker primary afferents respond with highly reproducible temporal spike patterns to transient stimuli. Here we show that, with the use of a linear kernel, any of these reproducible response trains recorded from an individual neuron can reliably predict complex whisker deflections. These predictions are significantly improved by integrating responses from neurons with opposite angular preferences.

In many sensory systems (1-3), including the rodent whisker-trigeminal system (4, 5), complex stimuli elicit sparse spike trains in individual neurons. Surprisingly, a small number of spikes may be sufficient for rapid sensory discrimination (6). This suggests that the nervous system extracts sufficient information from sparse spike trains to accurately encode complex stimuli (7, 8). To test this hypothesis, it is essential to reveal coding strategies used by first-order neurons in the sensory system, because these will constrain all subsequent processing and coding strategies. In the rodent whisker pathway, the first-order neurons are in the trigeminal ganglion.

To mimic whisker contacts during tactile discrimination, we deflected individual whiskers with a 2-s-long white noise waveform with frequencies from 10 to 125 Hz (Fig. 1A, middle column). We recorded well-isolated extracellular spikes from individual trigeminal ganglion neurons in response to 50 presentations of this stimulus. Data were obtained from four adult female rats, anesthetized with Nembutal and prepared for recordings as previously described (9). Because trigeminal neurons display a strong angular preference (9, 10), we applied the stimuli in each neuron's preferred direction. Figure 1B shows responses of an individual neuron. Most spikes occur at precisely the same time in every trial (11). These highly reproducible firing patterns suggest that a single spike train may contain sufficient information to encode the stimulus. We thus attempted to predict the stimulus from the recorded responses. We computed a linear kernel for stimulus-response pairs recorded during the first half of the stimulus. The kernel (K) identifies which features of the stimulus are present before each spike:

$$K=\frac{CS{D}_{(\text{spikes},\text{stimulus})}}{{\mathrm{PSD}}_{\text{stimulus}}}$$

where CSD_{(spikes, stimulus)} is the cross-spectral density between the spike trains and the stimulus and PSD is the power spectral density of the stimulus. We then convolved this kernel with each spike train recorded during the second half of the stimulus to derive the prediction. We estimated the accuracy of this prediction by computing the cross-correlation coefficient between the actual and the predicted stimuli (R^predict).

Fig. 1.

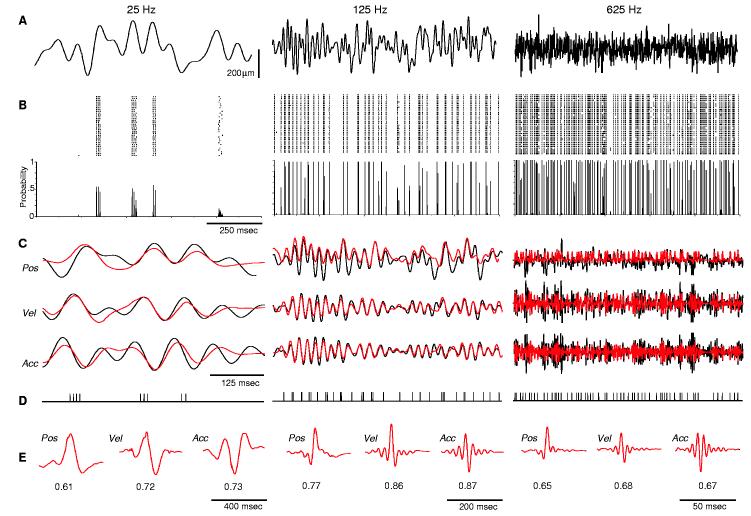
Single spike trains accurately predict complex stimuli. (A) Individual whiskers were stimulated 10 mm from their base by a piezoelectric device with white noise stimuli (10 to 25 Hz, 10 to 125 Hz, or 10 to 625 Hz) applied in each neuron's preferred direction. Upward deflections are in the preferred direction; downward deflections, opposite direction. Variability in stimulus waveforms was less than 5%. (B) Peristimulus rasters (top) and histograms (bottom) recorded from a trigeminal ganglion neuron in response to 50 presentations of each stimulus. Spikes were sampled at 10 kHz and sorted. msec, milliseconds. (C) Predictions (red) of actual stimulus (black) position, velocity, and acceleration at the three frequencies tested. (D) Individual spike trains used to compute the stimulus predictions in (C). (E) Kernels calculated for each of the stimulus parameters predicted in (C), with cross-correlation values between the original and predicted waveforms below the curves. Pos, position; Vel, velocity; Acc, acceleration.

We illustrated this process for one neuron in Fig. 1C (middle column). The original stimulus features (black trace) are well captured by the predicted stimulus (red). The prediction does not fully capture the peak amplitude of stimuli applied in the downward direction, because these deflections are in the cell's nonpreferred direction and produce no consistent spikes. Nevertheless, the predicted stimulus was highly correlated with the original stimulus. For the cell in Fig. 1, the prediction obtained by applying the kernel to a single spike train had a correlation coefficient, R^predict, of 0.77 (125-Hz position). Predictions computed from each of the other spike trains recorded from this cell were also highly correlated with the original stimulus (mean ± SD = 0.75 ± 0.01 and range of 0.73 to 0.77). We performed similar predictions from 15 additional neurons. For each of these cells, stimulus predictions were significantly correlated with the original stimulus (group mean R^predict = 0.66 ± 0.10 and an individual cell range of 0.45 ± 0.03 to 0.79 ± 0.02). We also computed, for each neuron, the coefficient of variation (CV) of R^predict for each of the 50 trials: The CV was <10%, indicating that a spike train from any individual trial provides an equally accurate prediction of the stimulus.

Trigeminal ganglion neurons respond more robustly to whisker deflections at high velocity or acceleration (10, 12). We therefore asked whether encoding of velocity or acceleration is more accurate than that of whisker position. Fig. 1, C and E, shows predictions for stimulus velocity and acceleration computed from the same spike train depicted in Fig. 1D. Both velocity and acceleration provided significantly better predictions than position [position R^predict = 0.75 ± 0.01, velocity R^predict = 0.85 ± 0.01, and acceleration R^predict = 0.86 ± 0.01; analysis of variation (ANOVA) with Tukey's honestly significant difference (HSD), P < 10^-5]. In 15 of 16 neurons, velocity and acceleration produced significantly better predictions than did position (P values < 0.01). Similarly, as a group, predictions of stimulus velocity (R^predict = 0.76 ± 0.12) and acceleration (0.77 ± 0.13) were significantly more accurate than position (0.66 ± 0.10, KruskalWallis, P = 0.004). This indicates that the neural code best captures abrupt changes in whisker trajectories. Such changes occur when a whisker contacts an object or when it encounters changes in an object's shape or texture. Neurons upstream in the whisker-to-barrel pathway also respond more robustly to high-velocity whisker deflections (13-15). Thus, whisker-based tactile discrimination appears to use a coding strategy similar to that of the visual system, in which neurons are sensitive to changes in contrast (16).

We therefore compared predictions of stimuli with different velocity content: white noise bandpass filtered at 10 to 25 Hz (25-Hz stimulus, velocity ≤ 1 μm/s, and acceleration ≤ 0.01 μm/s²), 10 to 625 Hz (625-Hz stimulus, velocity ≤ 20 μm/s, and acceleration ≤ 3 μm/s²), and 10 to 125 Hz (125-Hz stimulus, velocity ≤ 5 μm/s, and acceleration ≤ 0.2 μm/s²). We obtained high R^predict values from all three stimuli. For most neurons, predictions of the 25-Hz stimulus were significantly less accurate than those of the 125-Hz stimulus (position predictions significantly higher at 125 Hz for 14 of 16 neurons; velocity, 13 of 16 neurons; and acceleration, 15 of 16 neurons; ANOVAs, P values < 0.01). Deflections at such low velocities may be at or below the velocity threshold of these cells (10, 12). Predictions of the 625-Hz stimulus were also significantly less accurate than those of the 125-Hz stimulus (position predictions significantly higher at 125 Hz for 13 of 16 neurons; velocity, 13 of 16 neurons; acceleration, 12 of 16 neurons; P values < 0.01). The reduced R^predict values at 625 Hz may be confounded by the fact that the mean amplitude of this stimulus (37 μm) was smaller than that of the 125-Hz stimulus (56 μm).This is an unavoidable consequence of maintaining identical ranges of white-noise stimulus amplitudes while varying their frequency. Thus, the lower prediction values at 625 Hz may reflect an interaction between the velocity and amplitude sensitivity of these neurons (10, 12).

Alternatively, limitations inherent to the transduction process may limit decoding of stimuli at nonoptimal frequencies. If coding has its basis in limits of the transduction process, a different decoding mechanism (kernel) may be needed for different stimuli. We therefore asked whether a kernel computed from any stimulus could decode stimuli at other frequency ranges. We applied frequency-scaled kernels computed from higher frequency data to lower frequency spike trains (625- or 125-Hz kernels applied to 25-Hz data). Predictions obtained in this manner were unexpectedly accurate: Mean percent decreases in R^predict values were 5% (625 applied to 25 Hz) and 4% (125 to 25 Hz) (fig. S1). This suggests that encoding precision is constant across frequencies and that trigeminal neurons make use of a universal strategy to decode stimuli at all frequencies.

Different classes of somatosensory afferents may encode different qualities of som-esthesia. Trigeminal ganglion neurons are classified as rapidly adapting (RA) or slowly adapting (SA) (9, 10, 17). In response to ramp-and-hold stimuli, SA neurons produce more spikes (fig. S1), suggesting that they may better encode complex stimuli. However, in response to the white noise stimuli SA and RA neurons (n = 8 for each group) elicited similar mean spike counts at all frequencies tested (fig. S2). Indeed, RA and SA neurons provided indistinguishable R^predict values for every stimulus parameter (position, velocity, and acceleration) at every frequency tested (Kolmogorov-Smirnoff tests, P values > 0.32). We found no correlation between mean spike count and R^predict values for any parameter at any frequency tested (r values ≤ 0.13 and P values ≥ 0.14).

These findings indicate that mean spike counts do not provide a robust code for time-varying stimuli and suggest that precise spike timing is necessary to code these stimuli. We therefore randomly shifted the timing of individual spikes to determine the consequence of these jitters on stimulus predictions. We jittered every spike by varying time shifts (using Gaussian distributions of jitter, from ≤1 to ≤150 ms) (Fig. 2A) and computed kernels from these jittered trains to obtain stimulus predictions. Figure 2B plots normalized R^predict values as a function of jitter time shifts. Prediction values rapidly deteriorate as jitter is increased. We computed J₅₀, the jitter value that produced a 50% reduction in R^predict, as a measure of spike timing precision necessary to accurately predict each stimulus. The velocity J₅₀ values were 17.8 ± 3.1 ms (at 25 Hz), 6.8 ± 0.9 ms (125 Hz), and 1.6 ± 0.2 ms (625 Hz). This illustrates that precise spike timing is critical for accurate stimulus predictions; more rapidly varying stimuli require higher spike timing precision.

Fig. 2.

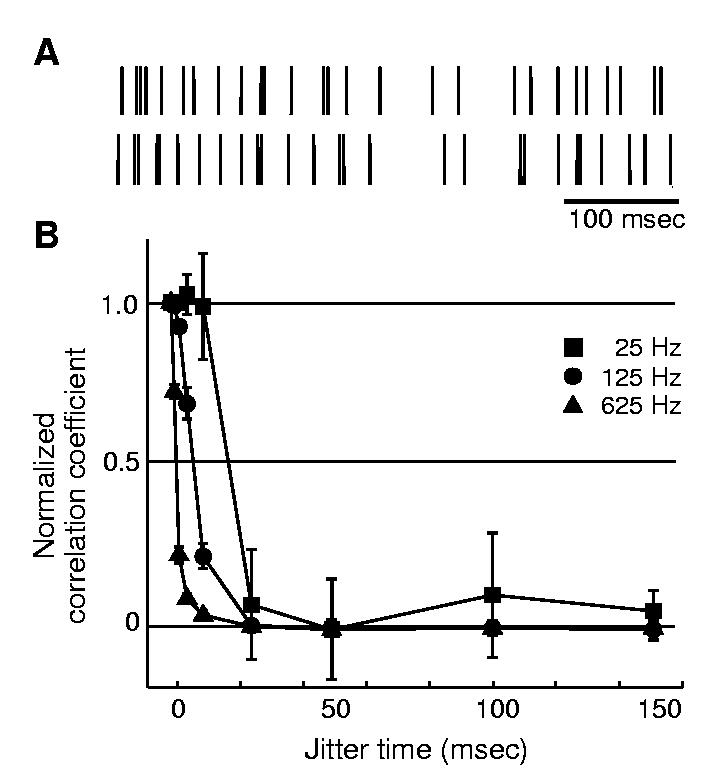
Shifting spike times degrades stimulus predictions. (A) The jittering process. Top raster is the original spike train in response to the 125 Hz stimulus, and bottom raster is the jittered train created by randomly shifting each spike from a Gaussian distribution of ±10 ms. (B) Prediction values degrade as jitter is increased. For clarity, only predictions of stimulus velocity are depicted. Correlation coefficients of the predictions were normalized to their unjittered value, and group data are plotted (mean ± SD) for all neurons (n = 16). Predictions degrade more rapidly for higher stimulus frequencies.

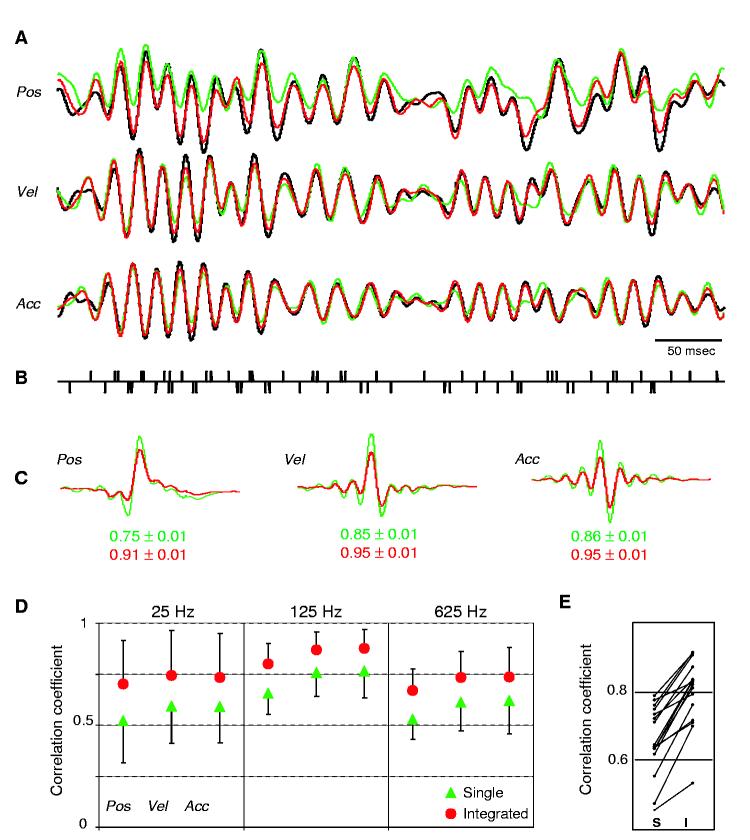
Our findings demonstrate that a single spike train from an individual neuron contains sufficient information to predict complex stimuli. However, whereas predictions accurately capture stimuli in the cells' preferred direction, they did not optimally predict deflections in the opposite direction (Fig. 1C). To obtain more accurate predictions, it might therefore be necessary to combine responses from neurons that are oppositely tuned. To mimic recording from two cells with opposite angular tuning, we presented to the same neuron the original stimulus and then its inverse. Spikes elicited in response to the original stimulus were integrated with spikes elicited by the inverse stimulus to compute kernels and to obtain predictions of the original stimulus. A similar approach was successfully used to compute reconstruction kernels from directionally selective neurons in the blowfly Calliphora vicina (18). Figure 3 demonstrates this analytical procedure for one neuron. The prediction computed from the integrated spike train now reliably captures deflections in both directions (Fig. 3A), and the prediction values improved significantly (for example, 125-Hz-position R^predict improved from 0.75 ± 0.01 to 0.91 ± 0.01, P < 10^-6). Similar significant improvements occurred in each of the 16 neurons analyzed for all stimulus parameters at all frequencies tested (Kruskal-Wallis, P < 10^-3) (Fig. 3E).

Fig. 3.

Prediction values significantly improve when integrating spikes elicited in response to stimulation in opposite directions. (A) Original 125-Hz stimulus (black), single predictions (green), and integrated predictions (red). (B) Integrated spike train used to compute the predictions in (A). Spikes in response to the original stimulus were assigned the value of +1; those in response to the reversed stimulus were assigned the value of -1. (C) Kernels used to compute the predictions in (A) and corresponding correlation coefficients: single (green) and integrated (red). (D) Group data (mean ± SD) for all neurons (n = 16). Prediction values increase for all stimulus parameters at all frequencies tested. (E) Integration significantly increases predictions for every neuron. Prediction values (125-Hz position) computed for single (S) and integrated (I) spike trains.

This suggests that integrating responses from neurons with different angular tuning is an effective way for neurons upstream in the somatosensory system to extract information about whisker deflections. The innervation of individual whisker follicles by multiple trigeminal neurons, having different angular preferences, ensures that the trigeminal population will accurately represent whisker deflections in every direction. Complete descriptions of multidirectional whisker deflections could then be extracted by upstream neurons through integration of these trigeminal spike trains. A coding mechanism based on a small number of precisely timed spikes in individual neurons might allow the whisker-trigeminal pathway to rapidly and accurately extract tactile features with the use of a limited number of whisker contacts (19, 20).