Simulating Force-Induced Conformational Transitions in Polysaccharides with the SMD Replica Exchange Method

Abstract

Conventional steered molecular dynamics (SMD) simulations do not readily reproduce equilibrium conditions of atomic force microscopy (AFM) stretch and release measurements of polysaccharides undergoing force-induced conformational transitions because of the gap between the timescales of computer simulations (∼1 μs) and AFM measurements (∼1 s). To circumvent this limitation, we propose using the replica exchange method (REM) to enhance sampling during SMD simulations. By applying REM SMD to a small polysaccharide system and comparing the results with those from AFM stretching experiments, we demonstrate that REM SMD reproduces the experimental results not only qualitatively but quantitatively, approaching near equilibrium conditions of AFM measurements. As tested in this work, hysteresis and computational time of REM SMD simulations of short polysaccharide chains are significantly reduced as compared to regular SMD simulations, making REM SMD an attractive tool for studying forced-induced conformational transitions of small biopolymer systems.

Recent atomic force microscopy (AFM) measurements of the elasticity of individual polysaccharide chains have observed large deviations from the simple entropic elasticity of polymer (1,2). The unusual elasticity of individual polysaccharide chains is characterized by pronounced plateau features in force-extension curves. It has been suggested that the pronounced plateau features are caused by force-induced conformational transitions that involve rotations of monomers about glycosidic linkages and various conformational transitions of sugar rings (1–7), whose atomic details have been revealed by steered molecular dynamics (SMD) simulations (8–10). SMD simulations have been extremely useful in interpreting experimentally measured force-extension relationships, but the gap between the timescales of computer simulations (up to ∼1 μs) and AFM experiments (∼1 s) means that SMD simulations of polysaccharides achieve qualitative rather than quantitative agreement with the experiment. Specifically, although the experimentally measured force-extension curves of polysaccharides are typically reversible (2), indicating that stretching of the polymer chain and force-induced conformational transitions of constituent sugar rings occur in equilibrium, there is a significant divergence between stretching and relaxing force-extension curves obtained from SMD simulations, which means that equilibrium has not been reached in computer experiments. It has been shown that in a near-equilibrium AFM stretching process, the force at which conformational transitions occur (transition force) is solely determined by the equilibrium constant between two conformations and not by the free energy barrier (11). In contrast, in a nonequilibrium stretching process, such as typically performed in regular SMD simulations, the transition force is influenced by the barrier and becomes dependent on pulling speed. Thus, better agreement between SMD and AFM experiments can be achieved only by slowing down the pulling speed (increasing the simulation time). Indeed, by slowing down the pulling/relaxing speed, near-equilibrium SMD simulations were achieved for the helix-coil transition process of deca-alanine in vacuum (12). However, as we will show, due to the complicated force-induced intra- and interresidue conformational transitions, even with ∼1 μs SMD simulations on dextran, a α-1→6 linked polysaccharide, the divergence between the stretching and relaxing cycles is still quite significant, making conclusions about the nature of modeled conformational transitions somewhat ambiguous. Therefore, it is important to find another approach that would circumvent these problems and bridge the gap between simulation and experiment on polysaccharides. Here we propose to use the replica exchange method (13) (REM) to enhance sampling efficiency during SMD simulations. With high-temperature replicas to overcome the energy barrier between two conformations and a sufficiently large exchange ratio between replicas, the phase space can be efficiently sampled even at the desired low temperature (e.g., 300 K). We employed combined REM SMD simulations to model the stretching and relaxation of the polysaccharide dextran, which has been extensively studied by AFM (1,2) and SMD (1,6). Using our novel approach, we produce forward and backward force-extension curves that display little hysteresis between them and reproduce the experimentally measured data not only qualitatively but also quantitatively.

Similar to standard REM MD simulations, in the REM SMD simulations, a set of SMD simulations (replicas) was conducted on the same molecular system over a range of temperatures. At different temperatures, the replicas exchange configurations at a fixed time interval, with a transition probability satisfying the detailed balance condition. The REM SMD simulations were performed with the Sigma program (14), and the regular SMD simulations were performed with the NAMD program (15). A 10-unit dextran fragment (213 atoms) was stretched and relaxed with the CSFF/CHARMM force field (16). The spring constant used in the simulations was 1.0 kcal/mol Å⁻², similar to the spring constant of the AFM cantilevers. The simulations adopted a time step 1 fs and a uniform dielectric constant 80. The REM SMD simulations were performed with 15 replicas distributed roughly exponentially between 300 and 900 K, with corresponding nearest neighbor acceptance ratios ranging from 29% to 35%.

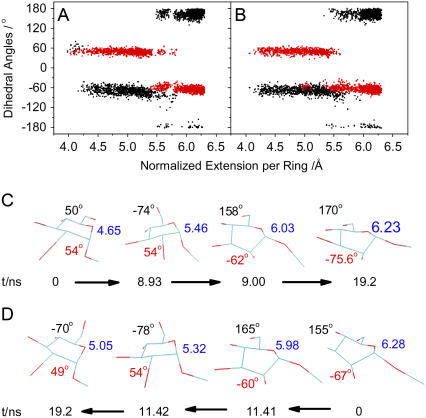
Fig. 1 compares the force-extension curves obtained from experiment and simulations, and Figs. 2 and 3 analyze in detail the conformational dynamics of ring 5, which is representative of the behavior of the other rings. We note, first, that even with long simulation times (800 ns stretching and 600 ns relaxing), the calculated force-extension curves from the regular SMD agree only qualitatively with the experimental one. Although both stretching and relaxing curves display the plateau feature characteristic of the experimental curve, the underlying conformational mechanisms are different, which cause a significant hysteresis between stretching and relaxing cycles of regular SMD simulations. This is evident in Fig. 2, which compares the behavior of the sugar ring during stretch (Fig. 2, A and C) and relaxation (Fig. 2, B and D). In the stretching process, the plateau feature represents a combined conformational transition that involves both forced rotation of the exocyclic group C5-C6 bonds and chair-boat transitions of the pyranose ring (characterized by the changes of the dihedral angle O1-C1-C2-O2). However, during the relaxing process, only C5-C6 bond rotations are observed, and the rings that started in boat-like conformations do not relax to chair conformations but remain in the boat-like conformation during the entire simulation. Second, short, ∼20 ns REM SMD simulations reproduce the AFM results fairly well, and the hysteresis between stretching and relaxing simulations is significantly decreased as compared to ∼800 ns regular SMD simulations. Moreover, the plateau features in the relaxing REM SMD simulation now involve both C5-C6 bond rotations and boat-chair transitions consistent with the stretching simulation (see Fig. 3, A–D). These self-consistent results strengthen the validity of our conjectured interpretation of the plateau feature in the force extension curve of dextran in terms of combined rotations and chair-boat transitions of the pyranose ring. Third, because little communication is required between replicas, REM SMD simulations take full advantage of parallel computation by letting each replica run on a separate computer node. In contrast, regular SMD simulations of small systems do not parallelize efficiently.

FIGURE 1 .

A comparison between force-extension curves of dextran obtained by AFM, REM SMD, and regular SMD simulations.

FIGURE 2 .

Conformational dynamics of ring 5 from regular SMD simulations. (A and B) Dihedral angles O6-C6-C5-O5 (black trace) and O1-C1-C2-O2 (red trace) during (A) 800 ns regular SMD stretching process and (B) 600 ns regular SMD relaxing process. (C and D) Time evolution of the structure of ring 5 from (C) stretching process and (D) relaxing process. The values of the dihedral angle O6-C6-C5-O5 are shown in black, dihedral angle O1-C1-C2-O2 in red, and O1-O6 distance in blue. The direction of the arrows denotes whether it is a stretching or relaxing process.

FIGURE 3 .

Conformational dynamics of ring 5 from the REM SMD simulations. (A and B) Dihedral angles O6-C6-C5-O5 (black trace) and O1-C1-C2-O2 (red trace) during (A) 19.2 ns REM SMD stretching process and (B) 19.2 ns REM SMD relaxing process. (C and D) Time evolution of the structure of ring 5 from (C) stretching process and (D) relaxing process. The color code is the same as in Fig. 2, C and D.

In summary, REM enhances the sampling efficiency and significantly reduces the computational time of SMD simulations, allowing them to approach near equilibrium conditions and thus correctly model AFM mechanical experiments on dextran. We expect the REM SMD combination to be a powerful means for interpreting force-extension relationships measured in AFM experiments on polysaccharides. It would be also interesting to use the REM SMD method to study other small biopolymer systems using implicit solvent models. We note that due to the complexity and the fact that the number of replicas needed scales as f^1/2 for a system with degrees of freedom f, the standard REM algorithm has only been proven to work well for small systems, as in this work. For simulations of large systems in explicit solvents, further work will be necessary to assess the performance of the standard or more advanced REM (e.g., Liu et al. (17)) combined with SMD.