Coupling of Global and Local Vibrational Modes in Dynamic Allostery of Proteins

Abstract

It is now recognized that internal global protein dynamics play an important role in the allosteric function of many proteins. Alterations of protein flexibility on effector binding affect the entropic cost of binding at a distant site. We present a coarse-grained model for a potential amplification of such entropic allostery due to coupling of fast, localized modes to the slow, global modes. We show how such coupling can give rise to large compensating entropic and enthalpic terms. The model corresponds to the pattern of calorimetry and NMR data from experiments on the Met repressor.

INTRODUCTION

It is now clear that dynamics plays an important role in protein function. For example, there is growing evidence for a dynamic contribution to allosteric signaling within protein molecules (1). Concepts introduced by Cooper and Dryden (2) have since been developed in coarse-grained theoretical models (3,4), detailed molecular dynamics (1,5,6), and computational normal mode analysis (7,8) including elastic network models (9–11). There is also a growing wealth of experimental evidence for protein dynamics in allostery (5,12) especially from NMR spectroscopy (13–18), neutron spin-echo spectroscopy (19), and fluorescence spectroscopy (20). Information on ligand binding can be communicated to a distant site in a protein via alterations of the global modes of vibration as well as by static conformational changes. High frequency modes are generally localized in proteins (21) and therefore are unable to communicate over large molecular distances. In this article, however, we investigate a mechanism by which such fast modes may contribute to the allosteric signaling by coupling to the global modes. We introduce and develop a simple theoretical model for such coupling and apply it to a specific example system, the Met repressor.

A strong experimental motivation for a model of this type arises from calorimetry (22) and NMR data (23) on the Met repressor. The Escherichia coli methionine repressor binds DNA only with its co-repressor S-adenosyl methionine (SAM), repressing the genes for the synthesis of the amino-acid methionine (22,24). The Met repressor is a dimer of two intertwined monomers, each with 104 amino acids, giving a dimer mass of 24 kDa. One SAM molecule binds to each monomer and the repressor dimer binds DNA with a β-strand binding motif (25). The Met operator contains 2–5 five Met boxes (tandem repeats of eight basepairs of similar sequence). Two dimers bind to DNA and form a dimer of dimers (26). The crystal structures of the holo- and apo-repressors (with and without co-repressor bound) show no significant conformation change on co-repressor binding (27). One theory to explain the activation of this allostery without conformational change is from long-range electrostatic interactions between the positive effector SAM and negative DNA phosphate groups (28). However, due to screening, electrostatic interactions are usually localized in proteins. An alternative suggested allosteric mechanism invokes changes in the flexibility of the repressor on ligand binding (22). This is supported by crystal structure B-factors (27), which show a stiffening of the protein on co-repressor binding. Initial results on the NMR structure and dynamics of the Met repressor indicate significant decreases in dynamics on SAM binding (23). Calorimetric data (22) indicate large compensatory entropic and enthalpic allosteric energies (∼20 k_BT). The entropic term is too large to be accounted for by the slow modes alone (a typical contribution of each degree of freedom in a global mode to entropic allostery is 0.5 k_BT (3)). There is also a large enthalpic component, yet this is unlikely to be due to major static conformational change, since the x-ray crystal structures show no structural change on effector binding (27). These observations motivate the search in this article for a model coupling fast modes to slow modes, which accounts for the effect in a way that retains the dynamic nature of the allosteric signal.

ALLOSTERY AMPLIFIED BY ENSLAVED FAST MODES

In this section we present a calculation of the vibrational allosteric free energy of a system that has fast, localized modes coupled to slow, global modes. The idea is that, by coupling to the delocalized global modes, despite their localized nature, the fast modes contribute to the allosteric communication. This contribution may result in an amplification of the allosteric signal. To make the idea more quantitative we begin with the scissor model of an allosteric protein drawn in Fig. 1 (the simplest case of slow-mode dynamic allostery). The model consists of two rods representing, for example, α-helices, with side chains indicated schematically. In this model there is one slow, delocalized mode (the scissor motion between the rods). There are several fast localized modes—the motions of the side chains of the α-helices. At this level we ignore the local, high wavenumber deformations of the stiff rods/helices, which also, in principle, contribute to the spectrum of fast modes. The key assumption of the model is that when the global mode is stiff (of low amplitude), the localized side-chain modes are also stiff. In this stiff case, the side chains will experience a more nativelike environment (a deep narrow native potential between the α-helices). This exposure to strong, specific interactions restricts their dynamics, corresponding to a deeper potential well for the motion of their degrees of freedom. However, if the amplitude of the flexible global mode increases, the enslaved side chains experience a different (and weaker) potential environment that is no longer as consistently exposed to close, specific interactions. We assume therefore that the potential seen by the fast modes is dependent on the instantaneous position x_s of the slow mode (or superposition of the slow modes for models with more than one enslaving slow mode). We assume that at all nonzero positions of the slow mode (x_s ≠ 0), the fast modes will experience a flatter potential than the native one seen at the minimum of the slow mode (x_s = 0). Increased motion of the slow mode, therefore, results in increased flexibility of the fast modes. On the timescale of the slow mode, the average motion of the fast modes appears increased. This is due to the fact that most of the time the side chains see a shallower and flatter potential, since the motion of the helices has displaced the side chains away from their native positions. At certain times within the trajectory of the slow mode the side chains will see their native potential and stiffen. This stiffening will be only temporary, however, before the global mode moves on and the side chains see a flatter potential again. Therefore, on the timescale of the slow mode, the average amplitude of the fast modes' motion will be correlated with the amplitude of the average motion of the slow mode.

FIGURE 1.

Single-mode scissor model of dynamic allostery. The rods represent α-helices. The side chains of such α-helices are shown schematically. Springs with spring constants k₁ and k_–1 are modified on binding to effector and substrate. The free energy for substrate binding is controlled by the amplitude of the thermally excited scissor mode, itself moderated by the presence of the effector.

Here we provide a calculation of this effect using the very simple scissor model shown in Fig. 1. This has just one slow global mode k_s controlled by the two effective springs, with spring constants k₁, k_–1 that are affected by ligand binding local to them (indicated by primed notation 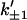). This is an allosteric model since the stiffening of one spring affects the vibrations of the other, due to the anchoring effect of the pivot point (which can be thought of as a spring of infinite strength). We assume that the system has N fast modes corresponding to the vibrations of the side chains shown schematically in Fig. 1. N such fast modes will arise from 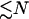side chains, since each side chain will contribute one or more fast-mode degrees of freedom. Our goal is to calculate the effect of coupled localized modes on the allosteric free energy ΔΔG, defined as the difference in the free energies of binding of the substrate at position (–1) in the two cases of the effector bound and unbound at position (+1). ΔΔG will naturally also be a function of the assumed changes to the local harmonic stiffnesses (k_–1 to 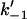and k₁ to 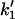) on binding.

To calculate the partition function as a route to the free energies of the model, we integrate over all the fast coordinates 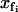and the slow coordinate x_s,

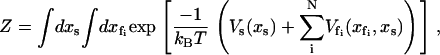(1)

for a single slow mode and N fast modes that are coupled to the slow mode. The quadratic approximation to the slow mode potential V_s is

(2)

The effective spring constant for the slow mode is k_s = k₁ + k_–1 (as in Fig. 1), where the effective spring constants k₁, k_–1 are affected by the binding of ligands local to them. The value 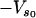is the minimum of the slow potential. If there is no coupling or the slow mode is infinitely stiff, the fast-mode potentials are, in the same harmonic approximation,

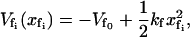(3)

where 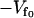is the minimum of the fast potential and k_f is the curvature, which at this level of calculation we assume to be the same for each fast mode. For a fast mode coupled to a finite slow mode, we modify the potential, Eq. 3, to

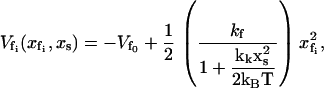(4)

where k_k is the coupling strength with dimensions of the force constant. Here, the choice of coupling function is arbitrary and chosen for analytical simplicity. By comparing Eqs. 3 and 4 it can be seen that the instantaneous position of the slow mode, x_s, smoothly decreases the curvature of the enslaved mode potential (as x_s → ∞ the curvature tends to zero). In this case we assume the depth of the enslaved mode remains constant. In Dynamic Enthalpic Allostery we will consider the case where the depth is also affected by the position of the slow mode.

Substituting Eqs. 2 and 4 into Eq. 1 and integrating over the fast modes, we obtain

(5)

where

(6)

The integral in Eq. 5 can be evaluated using the method of steepest decent in which the approximation

(7)

is made, where 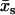is the maximum point of the function f(x_s). For 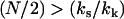, , 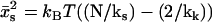leading to

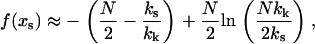(8)

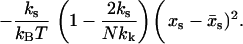(9)

The above case (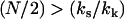) is appropriate, since N ≫ 1, and we assume that at the mean displacement of the slow mode, the fast-mode potential is modified by order-one changes to 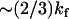or, equivalently, k_k ∼ k_s. The coupling of the fast modes to the slow mode therefore renormalizes the slow-mode spring constant to an effective spring constant, 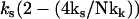. Substituting this into Eq. 5 and integrating gives

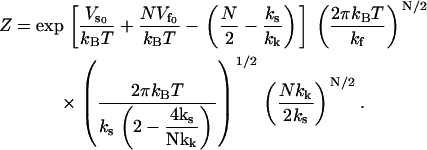(10)

From this partition function, we can find the free energy of the system:

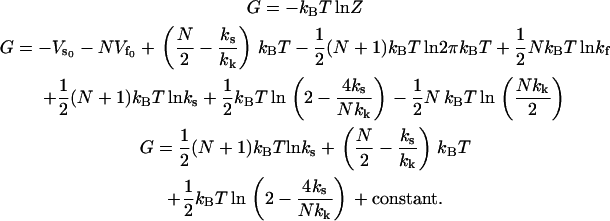(11)

Equation 11 lists explicitly only the terms that change on ligand binding. In Eq. 12 we apply the approximation 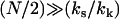for large N and k_k and substitute k_s = k₁ + k_–1 for the simple scissor model:

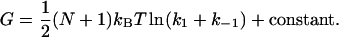(12)

Comparing this to the form with no enslaved modes, 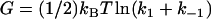, it is clear that enslaving N modes provides a strong amplification of the allosteric free energy. Interestingly, providing 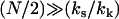, the free energy is independent of the coupling strength k_k. For the simple scissor model, modeling a ligand binding in the locality of k_–1 by a stiffening to k′_–1 (e.g., binding to DNA) in the two cases of apo k₁ and holo k′₁, the allosteric signal ΔΔG = ΔG_holo – ΔG_apo is given by

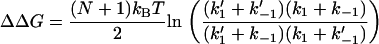(13)

For isothermal changes, this free energy change is purely entropic ΔΔG = −TΔΔS.

This first model produces a large, purely entropic, allosteric free energy. However, it cannot account for the allostery of the Met repressor, since the latter shows large compensating entropic and enthalpic terms. The potentially large amplification of the entropic allostery (Eq. 13) might well modify the calculation of ΔΔG for systems in the class of the Lac repressor (3). In this light, all slow-mode-only calculations give a lower bound to ΔΔG. However, further modifications of this model will clearly be required to produce a candidate theory for the Met repressor. We detail one in the following section.

DYNAMIC ENTHALPIC ALLOSTERY

In this section, we repeat the calculations in Allostery Amplified by Enslaved Fast Modes allowing the minimum of the potential seen by the fast modes to be affected by the position of the slow mode as well as the curvature. This is a much more realistic model because the depth, as well as the curvature, of the fast-mode potential is likely to be affected (to a different extent) by the slow mode. In this case we model the potential for the fast modes using two coupling functions of x_s. The coupling to the well-depth (shallowing) and to the well-width (flattening) are parameterized by the constants k_v and k_k, respectively. We choose for convenience to give these the dimensions of spring constants, as in the previous section. Now Eq. 3 becomes

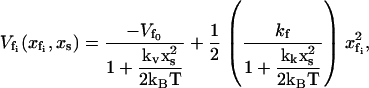(14)

in place of the form of Eq. 4. Substituting Eqs. 2 and 14 into Eq. 1 and integrating over the fast modes gives

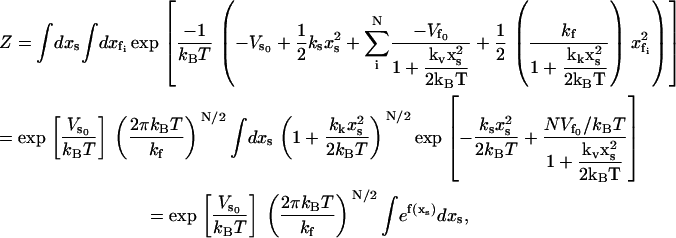(15)

where

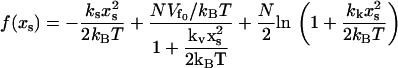(16)

As in Allostery Amplified by Enslaved Fast Modes, we use the method of steepest decent (Eq. 7). In this case, the maximum 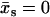for 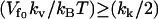(assuming 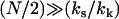) leads to

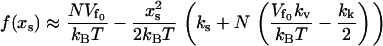(17)

Substituting this into Eq. 15 and integrating gives

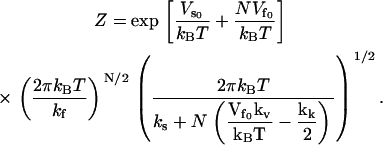(18)

The free energy G = –k_BT ln Z is therefore

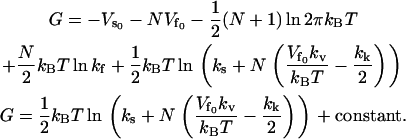(19)

As can be seen from Eq. 19, the free energy is not linear in N, so it does not show the amplification obtained in Eq. 12. In fact, in this case, for finite N and 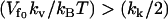the allosteric free energy is less than that for no-enslaved-modes N = 0. In the simplifying case of 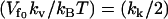, we obtain the nonenslaved result. However, this free energy hides enthalpic and entropic terms that are each affected strongly by the enslaved fast modes. Calculating the enthalpic and entropic terms separately (assuming isothermal changes) gives

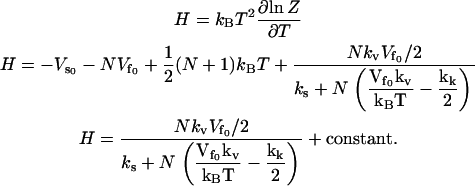(20)

This gives a large (linear in N) dynamic enthalpy contribution to the allosteric free energy where the enthalpy change is favorable for a stiffening of k_s. The entropy 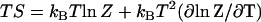includes this same term 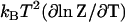. Thus this term cancels in the free energy ΔG = ΔH − TΔS. In this way, the favorable enthalpy of binding pays for the entropic cost of stiffening the protein.

If the enslaved fast localized modes are side chains at the DNA binding site, the potential that is affected by the slow-mode vibrations is the potential between the protein and the DNA (i.e., the static enthalpy of binding DNA). In this way the vibrational dynamics of the slow modes of the free repressor affects the static enthalpy of binding to DNA, causing a dynamic enthalpy contribution to the allostery. In this case, the enthalpy of binding to DNA, from Eq. 20 in the simplifying case of 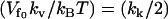, is

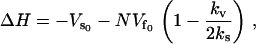(21)

where 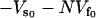is the static enthalpy of binding DNA. We have made the assumption that the potential minimum seen by the DNA binding site in the free repressor is zero and that seen in the complex with DNA is 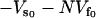. It can be clearly seen from Eq. 21 that the stiffer the slow-mode k_s, the more enthalpically favorable the DNA binding. The allosteric enthalpy has a dynamic component,

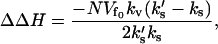(22)

where k′_s is the slow-mode stiffness of the free holo-repressor and k_s is that of the free apo-repressor. To obtain this equation we have assumed no static enthalpy change (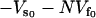 is unchanged on effector binding). The dynamic allostery is enthalpically favorable if the holo-repressor is stiffer than the apo-repressor. Since Eq. 22 is linear in the number of enslaved modes N, this contribution can be very large. We can easily extend this result for more than one slow mode coupled to the fast modes by replacing k_s with |K_s|, the modulus of the matrix of slow-mode stiffnesses. There will be a compensating unfavorable entropy component to this allostery given by

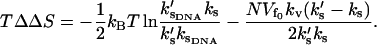(23)

The allosteric free energy will be the much smaller value

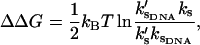(24)

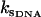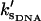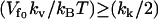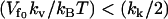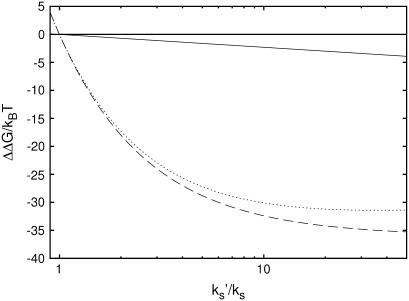
which is the same as that for no enslaved modes. The values and are the slow-mode stiffnesses of the apo-repressor complex with DNA and the holo-repressor complex with DNA, respectively. This exact cancellation of the enslaving effect between the enthalpic and entropic terms is true for . For the other case , the result will interpolate between Eq. 24 and the k_v = 0 result (Eq. 13) discussed in Allostery Amplified by Enslaved Fast Modes. So the condition 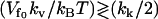actually separates two classes of qualitatively different behavior, giving zero or finite amplification to the net allosteric free energy. The large compensatory ΔΔH and ΔΔS values seen in the class discussed in this section, leaving a modest ΔΔG, is precisely the behavior seen in the calorimetry of the Met repressor. The plots of Eqs. 22–24 against the slow-mode spring constants ratio, k′_s/k_s, in Fig. 2, clearly show the compensating behavior.

FIGURE 2.

Graph of the dynamic allosteric free energy, ΔΔG, from Eq. 24 (solid) and the enthalpy ΔΔH from Eq. 22 (dashed) and entropy ΔΔS from Eq. 23 (dotted) components of this, against the stiffening of the effective slow-mode spring constant on corepressor binding to the apo-repressor, k′_s/k_s. For two tandem binding repressor dimers, the values plotted are twice those given in Eqs. 22–24. The graph is drawn for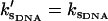, N = 12, 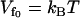, and k_v = 3k_s (see Application to the Met Repressor for a discussion on the choice of these values).

APPLICATION TO THE MET REPRESSOR

In this section we apply the theory described in Dynamic Enthalpic Allostery to the Met repressor as an example-case, discuss the choice of parameters, and compare the results with known experimental work. From normal-mode calculations we deduce parameters that reproduce observed thermodynamics.

To compare the theory described in Dynamic Enthalpic Allostery (Eq. 22) with experimental observations we need to make various assumptions about the values of the parameters used. Firstly, we assume the depth of the fast-modes potential is of the order of the strength of one hydrogen bond, giving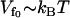. For the strength of coupling, we take the assumption k_v ∼ 3 k_s and k_k ∼ k_s, which is equivalent to saying that at the mean displacement of the slow mode, the fast-mode potential strength and stiffness is modified by order-one changes to 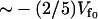and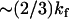. The resulting Eqs. 22–24 are not sensitive to the exact choice of k_k but are sensitive to k_v. Larger values of k_v give correspondingly lower modified fast-mode potentials and larger compensating dynamic entropic and enthalpic contributions to the allostery. We have chosen k_v ∼ 3 k_s to fit the observed compensatory enthalpy and entropy. The crystal structure of the Met repressor complex with DNA (protein data bank PDB ID: 1CMA (27)) reveals 14 side chains within 5 Å of DNA, six of which point toward the DNA. We assume the fast modes associated with these six side chains are enslaved and that each side chain contributes two fast modes (corresponding to librations parallel and perpendicular to the polypeptide backbone), giving an estimate of N = 12. Finally we assume 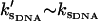. This means the slow-mode stiffness of the apo- and holo-repressors when complexed with DNA are of the same order, i.e., we assume the limit of large stiffening on DNA binding.

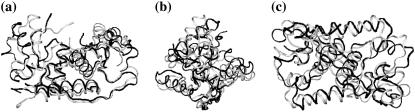
As an initial parameterization for k′_s/k_s, we use the six lowest collective normal modes of the Met apo (PDB ID: 1CMB) and holo-repressor (PDB ID: 1CMC) (27). These modes are stiffened on binding to DNA and to the co-repressor SAM. Choosing just the six lowest modes was found to be not-unreasonable for a coarse-grained model of the Lac repressor (3). We used the elastic network model software elNémo (29) (using the Tirion potential (30)) to calculate the normal modes, the lowest three of which are shown in Fig. 3. The ratio of the holo- to apo-repressor eigenvalues for the lowest six modes are given in Table 1. Since the modes calculated by elNémo are normal modes, we simply multiply the values of k′_s/k_s for each mode in Table 1 to obtain the ratio of moduli of the stiffness matrices of the holo- and apo-repressors, |K′_s|/|K_s|, for the combined effect of the lowest six modes. Interestingly the value obtained (≈11) corresponds to the start of the plateau-type behavior of the compensatory terms seen in Fig. 2. Substituting this into Eq. 24 and multiplying by two for the two dimers gives ΔΔG ∼ −2.4 k_BT. For a model at this level, this value compares favorably with the equilibrium measurements (28) ΔΔG = −5.5 k_BT, since all direct static enthalpic contributions are ignored. A similar pattern of dynamic allostery contributing approximately one-half of the total emerged in analysis of both the Lac repressor (3) and dynein (4) systems. The parameter values discussed, including the tuned value of k_v ∼ 3 k_s, reproduce to the correct order the enthalpic contribution to the dynamic allostery, ΔΔH ∼ −32 k_BT seen in the isothermal titration calorimetry experiments (22). Furthermore, the measured thermodynamics show a lack of temperature-dependence (22), consistent with the lack of static conformational changes seen in the crystal structures (unlike protein-DNA systems with linearly temperature-dependent compensating enthalpies and entropies thought to be due to the hydrophobic effect (31)). Our calculated dynamic enthalpy and entropy terms (Eqs. 22 and 23) are independent of temperature, so they are candidate explanations for the observed calorimetry.

FIGURE 3.

Met apo-repressor modes calculated by elNémo. The equilibrium structure is shown in black and the structure perturbed along the three lowest frequency modes are shown in gray. (a) Lowest mode (cleft-opening): a rotation that opens a cleft in the protein at the top of figure. (b) Second lowest mode (scissor): a rotation perpendicular to the first mode that causes the monomers in the Met dimer to move respect to each other in a scissor motion. (c) Third lowest mode (rocking): a rotation about the other perpendicular axis resulting a rocking mode.

TABLE 1.

Ratio of eigenvalues for the lowest six modes of the Met holo- and apo-repressor calculated by elNémo

Mode	k′s/ks
1	1.44
2	1.49
3	1.64
4	2.07
5	1.27
6	1.17

The simple theory discussed in this article makes some predictions of NMR spectroscopy data of backbone and side-chain dynamics. We expect the backbone amplitudes across the protein structure x_s to decrease by in the holo-repressor compared to the apo-repressor. The side-chain amplitudes near the DNA binding site x_f, however, will reduce by . This value is obtained by comparing the holo- and apo-values of the effective fast-mode spring constant at long times (for which ) and using the assumption k_k ∼ k_s. This predicted reduction will be smaller if the number of enslaved modes is larger than our assumed value of N = 12 and is also sensitive to the choice of k_v. We expect side chains that are distant from the co-repressor and DNA binding sites to show no change in dynamics on effector binding in comparison to slower backbone dynamics showing decreased dynamics far from the co-repressor binding site due to the delocalized nature of the slow modes. Initial analysis of NMR data on the Met repressor (23) indicates a qualitative agreement with these predictions of changes in dynamics on co-repressor binding. More quantitative analysis of the NMR data in the light of the theory presented here, should be possible in the future.

DISCUSSION

Our model allows us to collect the distinctive characteristics of systems that employ enslaving mechanisms: compensating, temperature-independent, dynamic entropic and enthalpic contributions to the allosteric free energy, and correlated changes to amplitudes of global and local modes. We expect repressor proteins, such as the Met repressor, that have these characteristics, to use an enslaving mechanism. For repressor proteins, such as the Lac repressor, which do not show these characteristics, we expect negligible enslaving effects. There are structural reasons to expect the Met and Lac repressors to belong to different classes. The Lac repressor monomers are internally rather rigid and communicate via an approximately planar interface. There is consequently little opportunity for the side chains within each monomer to couple strongly to their relative motion. The interface between the Met monomers, on the other hand, is highly convoluted and contains many more side chains that may be affected by slow global modes. There may exist repressor proteins that display behavior between these two limiting cases—that is, small but not negligible enslaving effects (for example, the core-binding factor, CBF (32)).

We have extended previous work on the lowest frequency modes (3) to consider the case of high frequency modes that are coupled to these global modes. This results in a dynamic model of compensating entropic and enthalpic terms in the allostery. Applying this to the example of the Met repressor reasonably explains the observed temperature-independent compensating enthalpic and entropic contributions to the allosteric free energy. We showed, in principle, how large amplifications of entropic allostery can be obtained if fast localized modes are enslaved to slow global modes. The model suggests both detailed molecular simulations and experiments that correlate NMR-derived information on dynamics with calorimetry thermodynamics measurements.