Bistability of Cell-Matrix Adhesions Resulting from Nonlinear Receptor-Ligand Dynamics

Abstract

Bistability is a major mechanism for cellular decision making and usually results from positive feedback in biochemical control systems. Here we show theoretically that bistability between unbound and bound states of adhesion clusters results from positive feedback mediated by structural rather than biochemical processes, namely by receptor-ligand dissociation and association dynamics that depend nonlinearly on mechanical force and receptor-ligand separation. For small cell-matrix adhesions, we find rapid switching between unbound and bound states, which in the initial stages of adhesion allows the cell to explore its environment through many transient adhesions.

In cell-matrix adhesion, cells use integrin-based contacts to collect information about their environment (1). The integrin receptors form two-dimensional clusters in the plasma membrane and are stabilized by connections to the cytoskeleton. Their extracellular domains reversibly bind ligands from the extracellular matrix like fibronectin, which present the ligand epitope through a polymeric tether. To efficiently explore a newly encountered surface and to commit itself to adhesion only if an appropriate combination of local signals is present, it is favorable for cells to start by establishing many small and transient adhesion sites. In the following, we introduce a simple theoretical model that predicts that small cell-matrix adhesions are characterized by bistability between bound and unbound states due to well-established principles of receptor-ligand dynamics. For biochemical control structures, positive feedback is well known to result in bistability and switch-like behavior, for example in the cell cycle and in the MAPK-cascade (2). Here we show that bistability in biological systems can also result from structural processes.

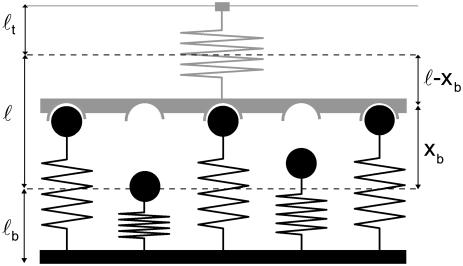
Fig. 1 shows the model studied in the following. The mechanical properties of the cell envelope holding the receptors and of the polymeric ligands are represented by harmonic springs. We consider a situation in which N_t receptor-ligand pairs are arranged in parallel along the cell-substrate interface. At a given time t, there are i closed and N_t-i open bonds. The dynamic variable i ranges from 0 (completely unbound state) to N_t (completely bound state). The probabilities for the N_t + 1 states are denoted by p_i(t) (0 ≤ i ≤ N_t) and their time evolution is described by a one-step master equation

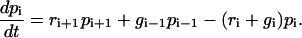(1)

FIGURE 1 .

Schematic representation of our model for an adhesion cluster with N_t bonds, out of which i are closed at a given time (here N_t = 5 and i = 3). The force transducer at the top and the ligand tethers at the bottom are modeled as harmonic springs, with rest lengths ℓ_t and ℓ_b and spring constants k_t and k_b, respectively. The positions of the unloaded springs (dashed lines) are separated by the unloaded receptor-ligand distance ℓ. The extensions of the loaded transducer and bond springs are denoted x_b and x_t = ℓ − x_b, respectively.

This equation states that i can either decrease due to rupture of a closed bond (reverse rate r_i) or increase due to binding of an open bond (forward rate g_i).

The reverse rate is r_i = ik_off(i) because any of the i closed bonds can be the next to break. The single bond dissociation rate increases exponentially with force according to the Bell equation, k_off(i) = k₀exp(F_b(i)/F₀), with the unstressed dissociation rate k₀ and the internal force scale F₀ (3). The force F_b(i) acting on each of the closed bonds changes dynamically and follows from mechanical equilibrium for the arrangements of springs depicted in Fig. 1:

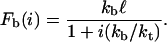(2)

Here, k_b represents the stiffness of the polymeric tethers carrying the ligands and k_t represents the effective stiffness of the cell envelope. The distance ℓ is the average distance between receptors and ligands if the cluster is completely unbound. Equation 2 shows that the more bonds are closed, the less force acts on the single bonds because it is shared between all closed bonds in the cluster.

The forward rate is g_i = (N_t-i)k_on(i) because each of the N_t-i open bonds can be the next to close. The single bond association rate increases as the receptor-ligand distance x_b(i) decreases and can be written as

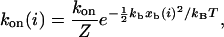(3)

where Z is the partition function for a ligand in a harmonic potential confined between −ℓ_b and x_b(i), k_on is the single bond on-rate if receptor and ligand are in close proximity, and x_b(i) = F_b(i)/k_b follows from Eq. 2. In our model, temperature T essentially controls ligand mobility: the larger T, the broader the ligand distribution. In the limit T→∞ (high ligand mobility, k_on(i) = k_on) and k_b ≫ k_t (soft transducer, F_b(i) = k_tℓ/i), our model simplifies to a case that has been used before to study the stability of adhesion clusters under force (4). However, only the full model introduced here results in bistability.

To demonstrate that our model leads to bistability, it is sufficient to consider the mean number of closed bonds, 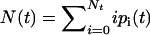. Neglecting deviations from the mean, the time evolution of N(t) is described by the ordinary differential equation

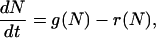(4)

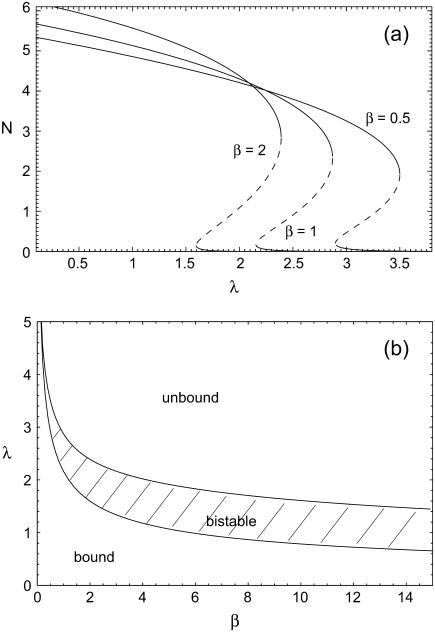
where reverse and forward rate are now interpreted as functions of a continuous argument. The same mean-field approach has been used before to study the stability of adhesion clusters under force in the limits of high ligand mobility and soft transducer, both for constant (3) and linearly rising force (5). In Fig. 2, we show the results of a bifurcation analysis of Eq. 4. In Fig. 2 a, stable (solid lines) and unstable (dashed lines) fixed points are shown as function of the dimensionless unloaded receptor-ligand distance λ=ℓ/ℓ_b and for different values of the dimensionless inverse ligand mobility 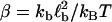. For small λ, a single, stable fixed point exists at finite N. Here, the adhesion cluster is bound because force on a closed bond is small and the density of free ligands close to the receptors is large, therefore rupture events are rare and can be balanced by rebinding. For large λ, there is a single, stable fixed point at N ≈ 0. Here, the adhesion cluster is unbound because forces are large and ligand density at the receptors is small, therefore rupture occurs frequently and cannot be balanced by rebinding. The transition from bound to unbound proceeds via a series of two saddle-node bifurcations, resulting in a window of bistability. This bistability results from two positive feedback mechanisms working in parallel. First, there is positive feedback for rupture: as one bond breaks, force on the remaining bonds is increased, thus increasing their dissociation rate. Second, there is positive feedback for binding: as one ligand binds, receptor-ligand distance is decreased and the binding rate for the other ligands increases. Fig. 2 a also shows that with increasing ligand mobility (decreasing β), the bistable region shifts to larger λ because the spatial distribution of ligands becomes broader, thus stabilizing adhesion clusters through rebinding. In Fig. 2 b, we construct a stability diagram by plotting the λ corresponding to the upper and lower bifurcation points as a function of β. Again we observe that λ decreases with increasing β. For the lower bifurcation, we find the scaling λ ∼ β^-1/2. For large β (small ligand mobility), the width of the two-state-region is fairly constant, whereas it decreases for small β (large ligand mobility) as the two curves converge.

FIGURE 2 .

(a) One-parameter bifurcation diagram showing stable (solid lines) and unstable (dashed lines) fixed points of the mean-field equation Eq. 4 as function of unloaded receptor-ligand distance λ = ℓ/ℓ_b and for three values of inverse ligand mobility, β = k_bℓ_b²/k_bT = 0.5, 1, and 2. The other parameters are N_t = 10, k_on/k₀ = 1, k_b/k_t = 1, and k_bℓ_b/F₀ = 0.1. (b) Stability diagram constructed from the location λ of upper and lower bifurcation points shown in a as function of β.

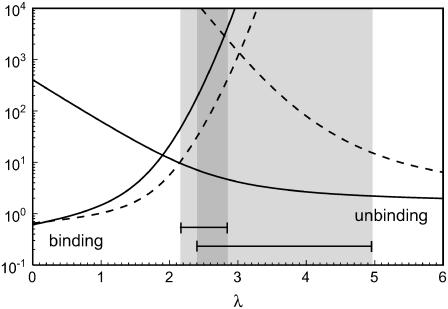
To study the dynamics of adhesion clusters, the full stochastic model of Eq. 1 has to be used. Bistability demonstrated in the bifurcation analysis of the mean-field theory now corresponds to bimodality of the stationary probability distribution. Again, coexistence of bound and unbound adhesion clusters is found for intermediate values of the unloaded receptor-ligand distance λ. In the stochastic description, the system is able to switch dynamically between these coexisting macrostates. Using Eq. 1, average binding and unbinding times can be calculated as mean first passage times (6). In Fig. 3, we plot average binding and unbinding times as function of the unloaded receptor-ligand distance λ for cluster sizes N_t = 10 (solid lines) and 25 (dashed lines). A detailed analysis shows that their ratio effectively equals the ratio of occupancy probabilities of the stationary solution of the master equation. Therefore when binding and unbinding times are equal, unbound and bound states are occupied with equal probability, thus defining a stochastic transition point. The shaded areas in Fig. 3 show the windows of bistability derived from the mean-field approach. For N_t = 10, the stochastic transition point is below the deterministic range, whereas for N_t = 25, it falls into the deterministic range. The definition of a range of bistability is less appropriate in the stochastic case because here the existence of a bimodal distribution is complemented by information on the transition times. For both deterministic and stochastic descriptions, the λ-values for bistability increase with N_t, so that for a given λ the bound state becomes the only stable macrostate when N_t grows. In the stochastic treatment, this leads to a super-exponentially fast increase of unbinding time with N_t for fixed λ, so that larger adhesions get effectively trapped in the bound state and only small adhesions will show bistable switching on an experimental time scale.

FIGURE 3 .

Average binding and unbinding times in units of k₀ as function of unloaded receptor-ligand distance λ = ℓ/ℓ_b for N_t = 10 (solid lines) and 25 (dashed lines) at β = 1. The other parameters are as in Fig. 2. The shaded areas marked by bars are the windows of bistability (which overlap in the darker region) from the mean-field theory for N_t = 10 (left) and 25 (right).

We finally discuss how our results apply to the integrin-fibronectin bond. For the low affinity fibronectin-α₅β₁-integrin bond k₀ ∼ 0.13 Hz and F₀ ∼ 10 pN have been measured (7) and we assume k_on/k₀ ∼ 1. Fibronectin is a semiflexible polymer with contour length L ∼ 62 nm, persistence length L_p ∼ 0.4 nm and equilibrium length ℓ_b ∼ 11 nm. Therefore the spring constant at small extensions can be estimated to be k_b = 3 k_BT/2 LL_p ∼ 0.25 pN/nm. From this we get k_bℓ_b/F₀ ∼ 0.27 and β∼ 7.1. To estimate the effective spring constant of the force transducer, we use the Hertz model for elastically deforming the cell with a cylinder of radius a. Then k_t = 2 aE/(1 − ν²) ∼ 0.27 pN/nm where we have used E ∼ 10 kPa for the Young modulus, ν ∼ 0.5 for the Poisson ratio and a ∼ 10 nm for the size of the adhesion cluster. Thus the ratio of force constants is k_b/k_t ∼ 0.9 and bistability for N_t = 5 is found from the full stochastic model around λ ∼ 0.75. The actual unloaded cell-substrate distance is the unloaded receptor-ligand separation ℓ plus the ligand rest length ℓ_b, that is 20 nm. This indeed is the range of cell-substrate distance at which mature cell-matrix adhesion starts (8).

In summary, our model predicts that the early phase of cell-matrix adhesion is characterized by rapid association and dissociation of small adhesion sites that have attachment times in the range of several tens of seconds. In the presence of appropriate signals, commitment to firm adhesion can be induced through different mechanisms, including recruitment of additional receptors and changes in binding affinity, which increase the escape time from the bound macrostate. In this sense, the structural mechanism for bistability described here resembles the switch-like behavior often encountered in biochemical control structures.